基于改进BP网络的高校科研项目评价模型

孙娓娓， 王先超， 王志刚

(阜阳师范学院 数学与统计学院， 安徽 阜阳 236041)

基于改进BP网络的高校科研项目评价模型

孙娓娓， 王先超， 王志刚

(阜阳师范学院 数学与统计学院， 安徽 阜阳 236041)

针对高校科研项目评审立项中主观性强的问题，提出了基于改进BP网络的项目评价模型.首先对于传统BP算法，在权值初始化加入混沌序列，并对权值修正过程加权优化，使网络具有收敛快、精度高的优点.然后设计了合理的项目评价指标体系，并给出了具体评价步骤.通过实例仿真说明，提出的改进BP算法用于评价科研项目科学客观，简单实用，有广泛的应用价值.

科研项目； BP网络； 混沌序列； 加权优化； 评价指标

科研项目是高校发展的基础，需要大量的资金、人才和设备的投入.因此，在科研项目立项过程中，客观公正地对申报的项目进行评价和筛选具有重要的理论和实际意义.目前，科研项目的评价方法主要有层次分析法(AHP)[1]、模糊评价法[2]和TOPSIS法[3].AHP是一种定性与定量相结合的分析方法，但构造的判断矩阵很难通过一致性检验.模糊评价法主要解决评价指标和权重带有模糊性的决策问题.TOPSIS法是一种距离综合评价法，其优点是对各决策方案进行排序比较.但这些传统的评价方法都有一个共同的缺点，就是评价指标的权重值都是人为给定，导致评价结果具有很强的主观性.

随着人工智能技术的发展，兴起了一些智能算法，如神经网络[4]、遗传算法[5]等.这些方法由于具有计算简便、结果合理以及受主观因素影响小等特点，为解决项目评价问题开拓了新领域.文献[6]提出了基于遗传神经网络的科研项目评价方法，该智能预算方法操作简单，预测精度高.但通过实例仿真说明，基于遗传神经网络的科研项目预算的平均相对误差比仅基于BP神经网络预算的误差要小两个数量级.也就是说基于耦合智能算法的科研项目经费预算方法更有效，预测精度更高.因此，智能算法的耦合优化在高校项目评审中的应用将是一个值得研究的焦点问题.

本文首先针对传统BP网络收敛慢的缺点，在权值初始化时加入混沌序列以增强多样性.同时在权值修正时进行加权优化，以解决收敛速度对样本顺序的过分依赖.然后将改进的BP网络用于高校科研项目的评估，从选题的必要性、技术的可行性、经费的合理性等重要因素建立评价指标体系.通过实例仿真，本文提出的评价模型更加客观实际，为高校科学地评审各类项目提供新的工具.

1BP算法的改进

BP网络是一种按误差反向传播算法训练的多层前馈网络，是目前应用最广泛的神经网络模型之一[7].它能学习和存贮大量的输入—输出模式映射关系，而无需事前知道描述这种非线性映射的数学方程.但BP网络自身也存在一些不足，如收敛速度慢、易陷入局部最小值、学习和记忆具有不稳定性等[8].因此，本文将从初始权值的选取、权值更新优化两个方面来改进BP网络，以期达到更好的收敛和预测效果.

1.1初始权值的混沌化

初始权值的选取对BP网络影响很大.若初始值靠近最优解，则网络收敛很快；反之收敛很慢甚至震荡.在标准BP算法中，初始权值通常是在[-1，1]区间上随机选取，或者通过GA、PSO等算法来优化[9].虽然这些方法有利于得到全局最优解，但同时具有盲目性、随意性和复杂操作性， 因此本文将采用一个新的初始值选取方法.

为了增加BP网络初始权值的多样性，这里引入混沌序列，这样能够保证初始化时，权值不存在重复性.混沌序列采用一维Logistic映射[10]

xn+1=μxn(1-xn)，

(1)

其中μ∈(0，4]为Logistic控制参数，xn∈(0，1)，n=0，1，…. 研究表明，当μ越接近于4，混沌序列xn就近似均匀分布在区间(0，1)，即具有较好的遍历性.

初始权值如下式所示:

wij=wmin+(wmax-wmin)k，

(2)

其中wij为神经元i到神经元j的初始权值，wmax，wmin分别为权值的上限和下限；k为混沌序列产生的随机数，即在(1)式中取初始值x0=0.3，控制参数μ=4. 但是由于混沌系统对初始值的选取很敏感[11]，因此本文先让迭代公式(1)计算20次后，再将结果值赋给k，这样可以保证数据的安全性.

1.2权值修正加权求和

训练样本的输入顺序对BP网络训练的结果有很大的影响.文献[12]已经证明，BP网络的收敛速度与样本的输入顺序所带来的样本特征差成正比.因此，BP网络更加容易记住后面出现的样本.如果每次都按照相同的顺序进行样本的读取，那么，当测试样本的输入接近较后的训练样本时，网络所输出的精度将明显的高.所以，算法不应根据一层不变的输入顺序对权值进行调整，而是用样本的“总体”去实现对权值的修改.在标准BP算法中，是通过批量处理来实现样本的“总体”.即当所有样本都正向学习完一次，计算网络的总误差

(3)

其中opi，ypi分别为输出层第i个神经元相对于第p个样本的期望输出和实际输出，m为输出层神经元的个数，N为样本总数.

当误差没有达到设定值时，然后再按照梯度下降法来反向修改权值

(4)

这种批量处理思想只是简单地对所有样本集求和，它没有体现每个样本对权值更新的不同贡献率.因此，本文采用组合预测的思想，对各个样本所引起的权值修正进行加权求和，使所有样本具有团结协作的精神，从而提高预测精度.具体公式如下：

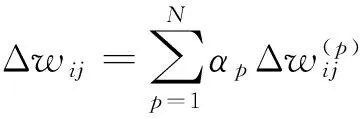
(5)

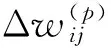
利用最优加权法求得最优的权系数为

α*=(R′E-1R)-1E-1R，

(6)

其中R为N维元素为1的列向量，E为误差信息阵.

2基于改进BP算法的高校科研项目评价模型

2.1评价指标

科学的评价指标，对科研项目的立项评审起着至关重要的决定作用.本文在参考他人研究的基础上[13]，并结合我校作为地方性师范院校的实际，提出了科研项目的主要影响因素为选题价值、研究方案和研究基础3个大类.每个一级指标下又由若干个二级指标组成，建立了如图1所示的评价指标体系.

图1 高校科研项目评价指标体系Fig.1 The evaluation index system of university research project

2.2基于改进BP网络的项目评价算法步骤

利用改进的BP网络评价科研项目包括两个部分：利用历史数据训练网络和应用网络对新项目进行评价.具体步骤如下：

1) 确定网络的拓扑结构.将图1中的9个二级评价指标作为网络的输入，项目的评价得分作为输出，隐层神经元的个数按经验公式[14]给出

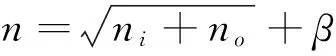
(7)

其中ni，no分别为输入层和输出层的神经元个数，β为1～10之间的整数.

2) 初始化.网络的初始权值由(2)式给出，设置预定的误差精度和最大迭代次数.

3) 对于每一个训练样本，按照(3)式前向计算误差.若误差大于精度，则按照(4)式反向逐层修改权值.

4) 当所有样本循环一次后，依据(5)式加权优化权值.

5) 反复以上步骤，直到满足误差精度或最大迭代次数.

6) 将训练好的网络进行新项目的评价.将待评审项目的9个评价指标输入网络，得到它们的综合评价分数.

图2 算法流程图Fig.2 The algorithm flow chart

3实例验证

现以我校2015年省自然科学研究一般项目为例.随机抽取50个项目，将评价指标分为优秀、良好、中等、及格、不及格5个等级，为了将指标量化，分别用10～8，8～6，6～4，4～2，2～0来表示各等级的范围.对于每个项目，请5位相关领域的专家对其打分，然后取平均值，得到原始数据样本如表1所示.

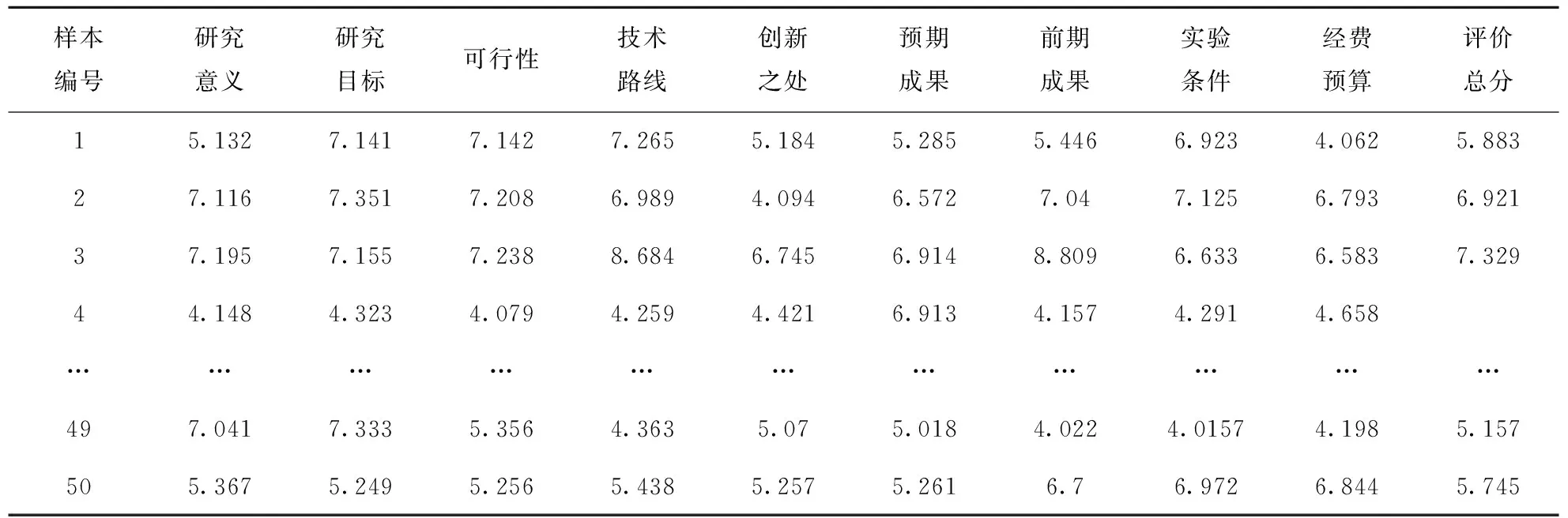
表1 项目评价数据

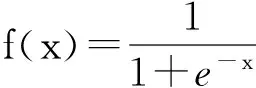
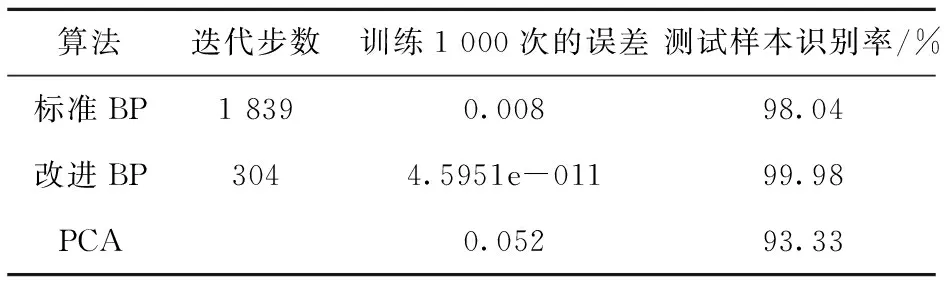
表2 不同模型的实验结果

从表2可以看出，本文提出的改进BP算法用更少的迭代次数就达到所需的收敛性，它比标准BP算法快了将近6倍.改进的BP算法比标准BP算法和PCA的误差精度提高了8个数量级.在测试样本的识别率上，改进的BP算法最好，将近100%，其实是标准BP算法，大概在98%，最差的是PCA.同时做出3种方法对测试样本的拟合效果，如图3所示.很明显，改进的BP网络的输出值与真实值的拟合度比另两种方法有大幅度的提升.实验证明，用本文提出的改进BP算法来评价项目，收敛快，精度高，能较好地满足实际需求.

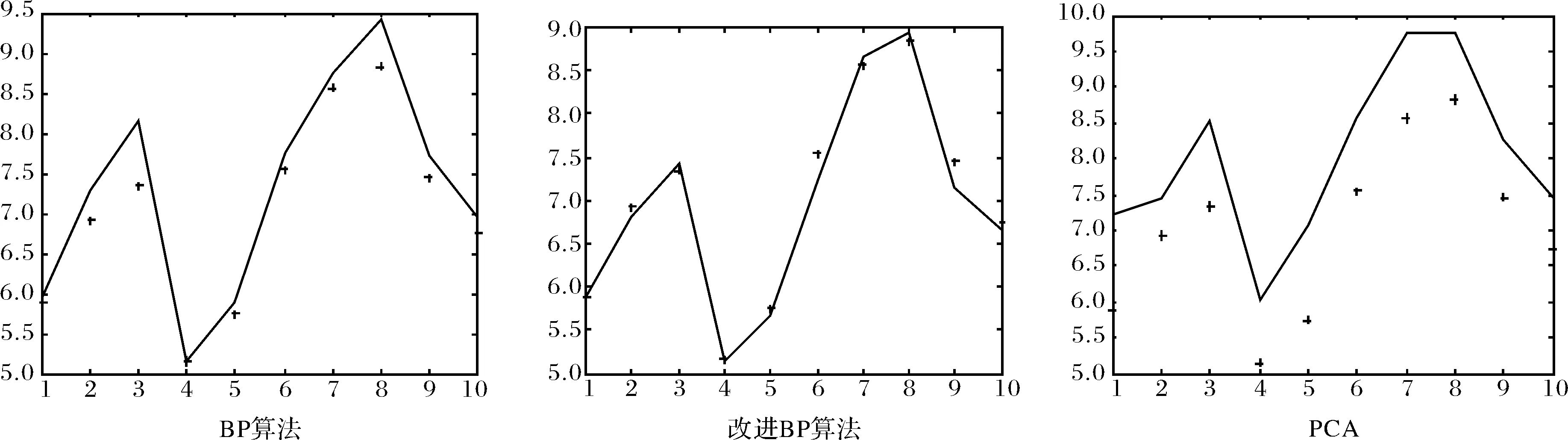
图3 测试样本的拟合效果Fig.3 Fitting effects of test samples

4结语

本文对BP算法从权值的初始混沌化和加权优化两个方面实现改进，体现了BP网络、混沌理论、组合预测等算法的联合优化.并用改进的BP网络对高校科研项目进行综合评价，确定合理的各级评价指标，根据BP网络的输出对科研项目进行比较.实例表明，以BP神经网络为代表的人工智能算法在科研项目评价分析中简单实用，有效地消除了主观因素的影响，为高校评审科研项目提供了科学可靠的评判标准.

[1] 刘长颖. 层次分析法与高校科研项目评估指标权重的确定[J]. 辽宁师范大学学报(自然科学版)， 2011， 34(1)：30-33．

[2] 宁宝权， 陕振沛. 基于改进熵和欧氏贴进度的模糊物元分析模型及应用[J]. 六盘水师范学院学报， 2015， 27(2)：79-83.

[3] 张守华， 孙树栋. 基于AHP和区间模糊TOPSIS法的高新技术科研项目评价[J]. 上海交通大学学报(自然科学版)， 2011， 45(1)：134-138．

[4] 杨 刚， 乔俊飞. 跨越—侧抑制神经网络分析及其应用[J]. 上海交通大学学报(自然科学版)， 2014， 48(7)：965-970．

[5] 佘春雨， 梁祥君. 进化神经网络法在科研项目评价中的应用[J].中国科技论坛， 2007(6)：107-109.

[6] 王国新， 王艺霖， 阎 艳. 基于遗传神经网络的科研项目经费预算方法[J]. 同济大学学报(自然科学版)， 2014， 42(8)：1298-1304．

[7] 杨 一， 高社生， 胡高歌. 基于敏感度方差重要性的RBF神经网路结构优化算法[J]. 控制与决策， 2015， 30(8)：1393-1398．

[8] 钱 坤， 王天真， 马 斌， 等.一种新型的局部连接BP网络模型及应用[J].系统科学与数学， 2014， 34(7)：792-804．

[9] 卓林超， 王 堃. 大数据中面向乱序数据的改进型BP算法[J]. 系统工程理论与实践， 2014， 34(6)：158-164．

[10] 李彩虹， 李贻斌， 赵 磊, 等. 一维Logistic映射混沌伪随机序列统计特性研究[J]. 计算机应用研究， 2014， 31(5)：1403-1406．

[11] 韩亚品， 胡珑瑛. 基于混沌理论的创新网络中组织间信任演化研究[J]. 运筹与管理， 2014， 23(4)：219-227．

[12] 朱旭东， 梁光明. 基于样本随机均匀分布的BP神经网络改进算法[J]. 数字技术与应用， 2014(8)：127-129．

[13] 张素娟， 黄晓燕， 邢少璟. 基于AHP和DEA的科研项目绩效评价方法研究[J]. 湖北师范学院学报(自然科学版)， 2012， 32(2)：6-11.

[14] 戴 珂， 张少仲， 蒋 波， 等. 基于多层前馈神经网络SPDS算法的地质数据非线性分析问题研究[J]. 计算机工程与科学， 2014， 36(8)：1528-1530．

[15] 董亚楠. 用于地方高校学费分析BP神经网络数学模型方法研究[J]. 计算机科学， 2014， 41(6)：481-483．

The evaluation model of university scientific research project based on improved BP network

SUN Weiwei, WANG Xianchao, WANG Zhigang

(School of Mathematics and Statistics, Fuyang Normal College, Fuyang, Anhui 236041)

In view of strong subjectivity in the review of university scientific research project, the evaluation model based on improved BP network is put forward. For the traditional BP algorithm, the chaotic sequence is joint to the weights initialization and update weights with weighted optimization. So the network has the advantage of fast convergence and high precision. The reasonable evaluation index system and specific evaluation procedure are designed. Through simulation examples, the improved BP algorithm used for evaluation of scientific research project in this paper is objective, simple and practical with widely application value.

scientific research project; BP network; chaos sequence; weighted optimization; evaluation index

2017-01-04.

国家自然科学基金项目(61672006，11401104)；安徽省自然科学基金项目(1508085MA12)；安徽高校自然科学研究重点项目(KJ2015A161)；阜阳师范学院自然科学重点项目(2017FSKJ05ZD).

1000-1190(2017)03-0273-04

O29

A

*通讯联系人. E-mail: 93692849@qq.com.