The existence of a nontrivial solution for abiharmonic equation with subcritical growth

XIE Dingyi， LUO Songhao， AI Wenhui

(School of Mathematics and Statistics， Central China Normal University， Wuhan 430079)

The existence of a nontrivial solution for abiharmonic equation with subcritical growth

XIE Dingyi， LUO Songhao， AI Wenhui*

(School of Mathematics and Statistics， Central China Normal University， Wuhan 430079)

In this paper, the following biharmonic problem is considered as

where Ω is a bounded domain ofNand

The problem is proved to have a nontrivial solution by applying the mountain pass theorem and the linking theorem respectively according to the different range ofλ．

nontrivial solution; biharmonic equation; (PS)ccondition

1Introduction and main results

In the last years， many authors have studied biharmonic equation

where Ω is an open bounded smooth domain ofN，λ≥0 andis the critical Sobolev exponent for the embeddingH2(N)→Lp(N)[1]. In this paper， we are interested in the existence of nontrivial solutions of this biharmonic equation with boundary condition(Ω).

Since several authors have studied the existence and behavior of nontrivial solutions for the corresponding second order elliptic problem at both critical growth and subcritical growth， it is more interesting to study the same problem for the fourth order. While the biharmonic equation combines many properties of the two second-order equations， it also poses much greater mathematical challenges， mostly due to the lack of a maximum principle．

The mountain pass theorem plays an important role in geometric analysis and partial differential equations. In 1973， Ambrosetti and Rabinowitz[2]have developped dual variational methods to prove the existence and estimate the number of critical points possessed by a real valued continuously differentiable functional. In 1978， Rabinowitz give some minimax methods in critical point theory in [3]， especially the linking theorem.[4]Thanks for their well-known results， these are several famous mountain pass lemma and its variants which have been applied frequently in order to establish the existence of critical points for functions．

We apply some basic minimax theorems to study the following problem

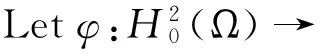
Since

〈φ′(u)，h〉=

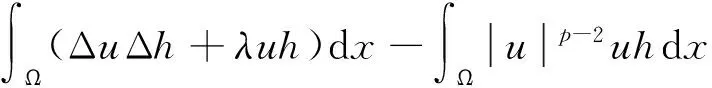
the critical points ofφare the weak solutions of (P). In the superquadratic case

it is easy to verify that

Our main results in this paper can be stated as follows:

Theorem 1. Suppose thatλ1=λ1(Ω) is the first eigenvalue of Δ2. Then the problem (P) has a nontrivial nonnegative solution if and only ifλ>-λ1．

Theorem 2. For everyλ∈， the problem (P) has a nontrivial solution．

Now let us outline the main idea to prove the main results. In order to prove Theorem 1， the main tool is the mountain pass theorem.[7]We have to check that the energy functionalφ(u) satisfies the mountain pass geometry and the (PS)ccondition holds respectively. In order to prove Theorem 2， noting thatλ∈and the energy functional does not satisfy the mountain pass geometry， in order to overcome this difficulty we will apply the linking theorem. So we have to check that the energy functionalφ(u) satisfies the linking geometry in this case．

The paper is organized as follows. In section 2， we apply the mountain pass theorem to prove Theorem 1. And we prove Theorem 2 by the linking theorem in section 3. In the appendix A， we give some known results which are used repeatedly in the proofs of our paper．

2Proof of theorem 1

In this section， we will mainly prove Theorem 1. First， we give the following basic result．

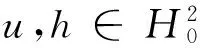
∫Ω(ΔuΔh+λuh)dx.

Similarly， we have

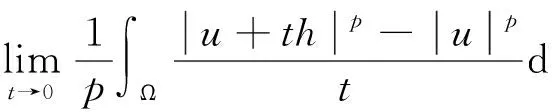
By the mean value theorem， there existsξ∈(0，1) such that

The Hölder inequality implies that

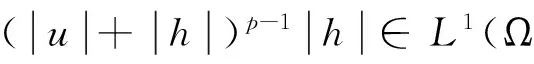
It follows then from the Lebesgue theorem that

So

〈φ′(u)，h〉=〈ψ′(u)，h〉-〈χ′(u)，h〉=

→0， asn→∞.

Soψ′(un)→ψ′(u)， asn→∞．

Similarly， we get

〈χ′(un)，h〉-〈χ′(u)，h〉=

〈χ′(un)-χ′(u)，h〉=

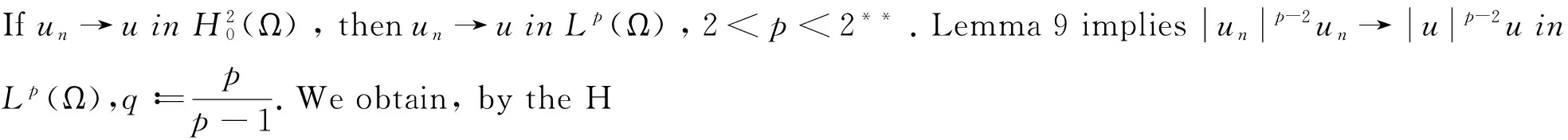
and so

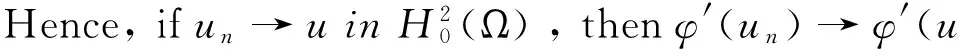
〈ψ″(u)h，v〉=

(ΔuΔv+λuv)]dx=∫Ω(ΔhΔv+λhv)dx.

So 〈ψ″(u)h，v〉=∫Ω(ΔhΔv+λhv)dx.

Similarly， we obtain

By the mean value theorem， there existsξ∈(0，1), such that

The Hölder inequality implies that

It follows then from the Lebesgue Theorem that

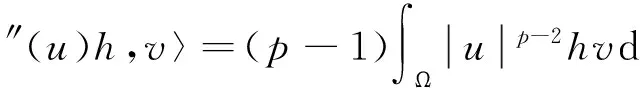
So

〈φ″(u)h，v〉=

〈ψ″(u)h，v〉-〈χ″(u)h，v〉=

and

〈χ″(un)h，v〉-〈χ″(u)h，v〉=

and so

Lemma 2φ(u) satisfies the mountain pass geometry．

Hence， we obtain

and there existsr>0 such that

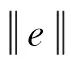
φ(un)→c，φ′(un)→0， asn→∞.

Under the assumption of Theorem 1， we have following lemma．

Lemma 3 (PS)csequence has a strong convergent sequence．

1) Fornbig enough， we have

φ(un)-p-1〈φ′(un)，un〉=

It is clear that

〈φ′(un)-φ′(u)，un-u〉→0，asn→∞.

It follows from the Hölder inequality that

Ifφsatisfies the (PS)ccondition， then c is a critical value ofφ．

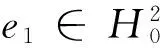
λ∫Ωue1dx=

-λ1∫Ωue1dx，

and thusλ>-λ1.

Sufficient condition. Combining Lemmas 1 to 3， applying Proposition 1， we know thatφ(u) has a critical value. So (P) has a nontrivial solution．

3Proof of theorem 2

In order to prove Theorem 2， we need the following lemmas．

Lemma 4 There holds

Sinceμ1<+∞，u≠0， we obtain

Let

μ1<μ2≤…≤μn≤0<μn+1≤…

be the sequence of eigenvalues of

where each eigenvalue is repeated according to it’s multiplicity. Lete1，e2，…,en，…be the corresponding orthonormal eigenfunctions inL2(Ω)．

Lemma 5 Under the assumptions of the preceding lemma， if

Y∶=span(e1，…，en)，

then

Proof By definition， onZwe have

δ=1+∫Ωλu2dx≥

Ifμ=0，δ=1 and ifμ≠0，δ≥un+1∫Ωu2dx>0.

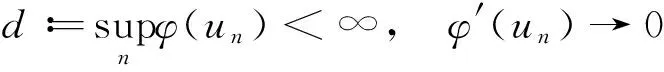
contains a converging subsequence．

Fornbig enough， we have

φ(un)-p-1〈φ′(un)，un〉=

where， according to Lemma 5，un=yn+zn，yn∈Y，zn∈Z.

It is clear that

〈φ′(un)-φ′(u)，un-u〉→0， asn→∞.

It follows from the Hölder inequality that

Lemma 7φ(u) satisfies the linking geometry structure．

Proof OnZ， it follows from Lemma 3.2 that

By Sobolev imbedding theorem， there existsr>0,such that

OnY， we have

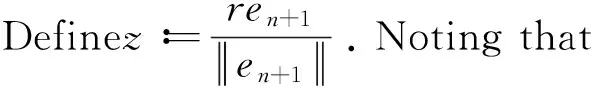
we have

Since， on the finite dimensional spaceY⊕z， all norms are equivalent， we have

Thus there existsρ>r, such that

where

Therefore， we have

Letφ∈C1(X，R) be such that

Ifφsatisfies the (PS)ccondition with

，

then c is a critical value ofφ．

[Proof of Theorem 2] Combining Lemmas 4 to 7， applying Proposition 2， we can complete the proof．

Appendix A Some basic and known results

In this section， we give some results which have been applied before. We shall not prove them．

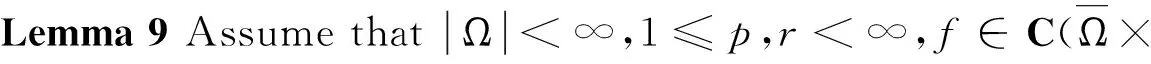
is continuous．

Acknowledgements The author sincerely thank Professor Peng Shuang jie and Associate Professor Wang Chunhua for helpful discussions and suggestions. This paper was partially supported by NSFC．

[1] CHAITAN P GUPTA， YING C KWONG. Biharmonic eigenvalue problems andLpestimates[J].Internat J Math Math Sci, 1990，13(3):469-480．

[2] AMBROSETT A， RABINOWITZ P H. Dual variational methods in critical point theory and applications[J]. J Funct Anal, 1973，14:349-381．

[3] RABINOWITZ P H. Minimax methods in critical point theory with applications to nonlinear partial differential equations[C]//Rhode Island: American Mathenatic Society,1986.

[4] BRIZE H， CORON J.M， NIRENBERG L. Free vibrations for a nonlinear wave equation and a theorem of P.Rabinowitz [J].Comm Pure Appl Math, 1980，33:667-689．

[5] WILLEM M. Minimax Theorems[M].Boston: Birkhäuser Boston，1996．

[6] GAZZOLA F， GRUNAU H C， SQUASSINA M. Existence and nonexistence results for critical growth biharmonic elliptic equations[J]. Calc Var Partial Dif, 2003， 18(2): 117-143．

[7] EVANS L C. Partial Differential Equations [M].2nd Ed. Rhode Island: Amer Math Soc, 2010．

2017-03-03.

国家自然科学基金项目(11671162).

1000-1190(2017)03-0282-06

一类带次临界指标的双调和方程非平凡解的存在性

谢定一, 骆嵩豪, 艾文会

(华中师范大学 数学与统计学学院， 武汉 430079)

该文主要研究以下的双调和问题

本文分别利用了山路定理和环绕理论证明了该问题在λ的不同范围下有非平凡解.

非平凡解； 双调和方程； (PS)c条件

O176.3

A

*通讯联系人. E-mail: 1312793452@qq.com.