基于本征正交分解法的液环泵气液两相流场重构

张人会 吴 昊 杨军虎 李仁年

(1.兰州理工大学能源与动力工程学院， 兰州 730050； 2.兰州理工大学甘肃省流体机械及系统重点实验室， 兰州 730050)

基于本征正交分解法的液环泵气液两相流场重构

张人会1,2吴 昊1杨军虎1,2李仁年1,2

(1.兰州理工大学能源与动力工程学院， 兰州 730050； 2.兰州理工大学甘肃省流体机械及系统重点实验室， 兰州 730050)

针对液环泵内复杂的气液两相流动、计算量大且优化设计难以进行的问题，提出了采用本征正交分解法进行液环泵内流场的重构分析。采用泰勒多项式对二维叶片型线进行参数化控制，通过对各控制参数进行适量的扰动得到叶片型线样本集。采用VOF模型进行液环泵内气液两相流场的数值模拟，由叶片型线参数及叶轮内流场数据构建样本的快照集，依照几何相似及网格变形方法插值得到各相似点的流场参数，依据本征正交分解(POD)法将快照集分解为正交基的线性组合。由最小二乘法拟合目标叶型所对应的正交基系数，实现了对目标叶片流场的重构。采用POD方法对2BE-203型液环泵内单个叶轮流道的气液两相流流场进行了重构，精确地重构了单个叶轮内流场结构的各个特征，除在气液交界面附近有一定的误差，整体预测结果具有较高的精度，大大减少了流场预估的计算量。

本征正交分解; 气液两相流; 液环泵; 网格变形

引言

液环泵是一种用来抽送气体的流体机械, 被广泛应用于低真空或低压缩比场合，其内部为具有不稳定自由分界面的气液两相流动，效率较低。由于复杂的内部两相流动约束导致其水力性能的优化设计进展缓慢。RAIZMAN等[1]采用压力探针测量了液环泵内液环的压力分布，并对液环的速度场进行了分析。KAKUDA 等[2]运用移动离子半隐式方法(MPS)对液环泵内部粘性流动进行数值计算，分析了不同转速下液环的形状、速度矢量等，并将计算结果与实验结果进行了对比。TETERYYUKOV等[3]提出了采用三段圆弧方法设计非圆柱形泵壳体来优化液环泵的性能。文献[4-5]运用CFD 软件对液环泵内部流动进行数值计算，分析了泵内两相流场的分布规律。张人会等[6]采用CFD方法对液环泵内气液两相流及其自由界面的复杂运动规律进行了研究。液环泵内复杂的气液两相流动导致其内流动数值模拟的计算量大大增大。

流体机械水力优化设计的流场计算量随着其设计变量的增加呈几何级数增加[7-9]，因此其水力性能优化问题的重点在于减少流场预估的计算量。为了减少流场的计算量，ANTONY[10]提出伴随方法(Adjoint method)，并将该方法应用于航空翼型的气动优化设计，该方法最大的困难在于要求解复杂的伴随系统。MOHAMMADI等[11]提出不完全敏感性方法来减少流场约束下几何边界的优化问题，但该方法有苛刻的适用条件。本征正交分解(Proper orthogonal decomposition，POD)法最早由HOTELLING[12]提出，是一种功能强大的数据特征提取方法，被广泛应用于低维湍流结构的描述[13]、结构振动分析[14]、图像处理[15]、PIV技术[16]、以及翼型流场的重构分析及其气动优化[17-19]。本文提出基于本征正交分解(POD)方法进行液环泵内气液两相流场的重构，避免其优化过程敏感性分析中的多次流场计算，减少优化设计的计算量。

1 液环泵流场分析

以2BE-203型液环泵为研究对象，对其内部复杂的气液两相流场进行重构分析，其结构如图1所示。

图1 液环泵结构图Fig.1 Structures of liquid-ring pump

其流动求解区域包括：叶轮、腔体、进气段、出气段和补液管。考虑其为双吸式泵，两侧流道完全对称，在计算过程中只模拟其单侧流动，对整个流动区域使用六面体结构化网格进行划分，网格总数1 091 166，其计算域网格如图2所示。

图2 液环泵求解区域网格Fig.2 Mesh of computational domain for liquid-ring pump

其中任一叶轮流道有39×30个网格单元，如图3所示。

图3 叶轮流道网格Fig.3 Blades mesh domain

液环泵额定工况为：进气压力p=40 kPa，进水流量Q=0.43 m3/h，转速n=1 170 r/min。液环泵内流动为具有非稳态气液自由分界面的气液两相流，气液分解面的形状对泵的性能有重要影响，为精确捕捉界面流动，采用VOF气液两相流模型[20]，采用RNGk-ε两方程湍流模型、理想气体定律、滑移网格、PISO算法，时间步长Δt=3×10-5s，由32核64 G内存小型工作站120 h计算后，得到较为稳定的压力、相态、速度场分布，如图4所示。

由图4可以看出压力由轮毂到壳体内壁、由吸气区到排气区逐渐增大；在泵壳体内壁形成近似等厚度的液环，气液交界面呈不稳定的锯齿形；流道内速度基本上从轮毂到壳体内壁逐渐增大，但从吸气区到压气区逐渐减小。

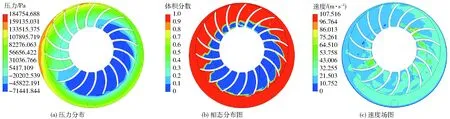
图4 流道截面的流场分布Fig.4 Flow distributions of channel section

液环泵性能曲线的模拟结果与实验结果对比如图5所示。实验结果由合作生产厂家的液环泵实验系统测试得到。

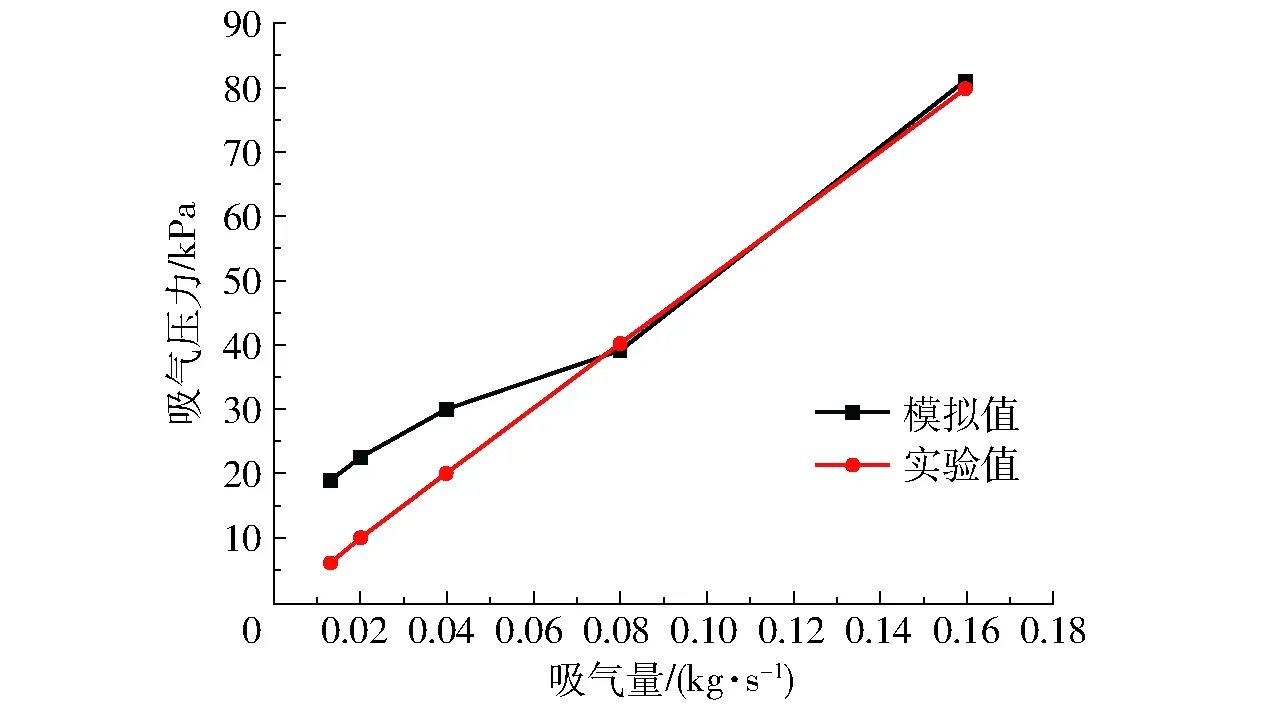
图5 模拟结果与实验结果对比Fig.5 Comparison of hydraulic performance between CFD and experiment

从图5可看到，随着进气口真空度的增大，其质量流量逐渐下降，当进气口吸气压力大于40 kPa时，其模拟值与实验值吻合较好，当进气口压力低于40 kPa时，模拟值与实验值之间有一定的偏差，随着进气口真空度的提高，液环泵内气液交界面变得越来越不稳定，VOF模型对自由界面的捕捉精度下降。本研究对液环泵流场重构分析中选定40 kPa工况作为预测工况。

2 Gappy POD本征正交分解方法

POD方法利用降阶技术对复杂系统进行特征分析，对样本集构成的矢量集进行本征正交分解，样本集矢量可表示为正交基的线性组合。POD方法常被用于缺失数据的填补。

样本快照集U为

U=[U1,U2]

(1)

在矢量集U1中，所有的元素都是已知的，而在矢量集U2中，部分元素是缺失的，所缺失的元素需要补充完整。矢量集U1为

(2)

式中，Φ是POD基础，可通过快照集U的奇异值分解计算得到，即

Φ=[Φ1,Φ2]

(3)

式中，Φ1、Φ2对应于快照集U1和不完整矢量U2的POD基础。

矢量U2可表示为

(4)

系数βj可通过最小二乘逼近法得到，即

Mβ=f

(5)

其中Mij=(Φi,Φj)，fi=(U1,Φi)，通过求解式(5)得到系数βj，所以不完整矢量U2可通过式(4)进行补充。

3 叶片型线控制方法和网格变形

3.1 叶片型线参数控制

由于液环泵叶片都属于二维圆柱形叶片，圆柱叶片型线上的点可以表示为：f(r,θ)=0。通过采用泰勒公式来表示叶片型线，任意叶片型线均可以表示为其初始型线基础上的泰勒展开，即

θ(r)=θ0+a1r+a2r2+…+anrn

(6)

在初始叶型的基础上对各控制参数进行扰动可得流场重构所需的样本集，本算例中以图6所示目标叶型附近的8个叶型作为初始样本集。

图6 样本叶片型线Fig.6 Blade shape curves of samples

3.2 相似网格及变形方法

POD方法是根据各样本叶型的内部流场对目标叶型内流场进行重构分析，由于各叶轮内流道几何相似，进行流场的重构时需要根据相似坐标进行流场样本集的构建，并进行流场的预测。因此对各叶轮样本的单个流道均进行39×30的结构化网格划分。而对部分由于计算过程收敛性要求对叶轮结构化网格进行细化的叶轮，在CFD流场分析完成后，采用网格变形技术重构其39×30的结构化网格，然后按照相似的网格节点进行流场的插值，从而得到各相似坐标点对应的样本矢量集。

定义沿着圆周角θ的无量纲坐标εi,j为

εi,j=(θi,j-θi,1)/(θi,30-θi,1)

(7)

式中θi,j为(i,j)节点所对应的圆周角坐标，类似地可定义r方向的无量纲坐标ηi,j。对于根据目标叶轮所生成的39×30的结构化网格可重构其他样本叶轮的结构化网格，如图7所示。

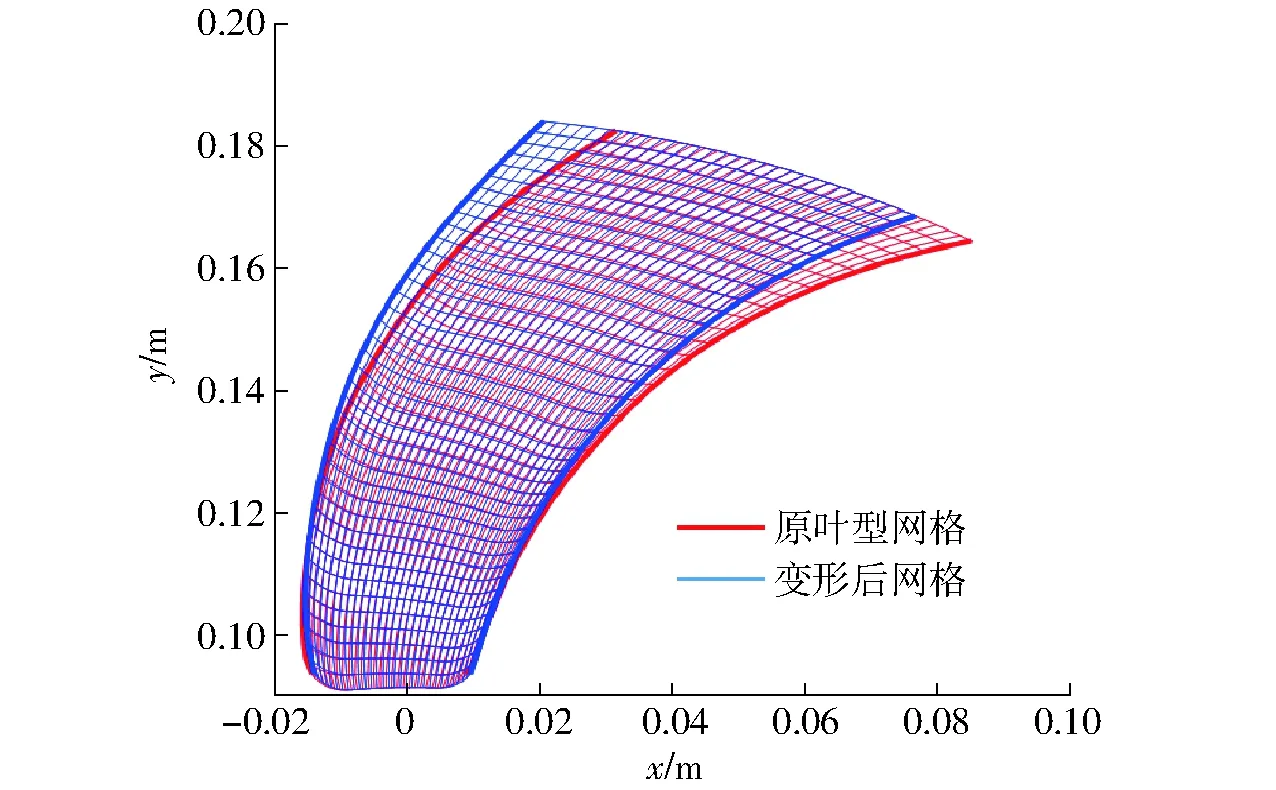
图7 网格变形对比Fig.7 Comparison of mesh deformation

4 叶轮内流场的重构及其误差分析

由此可得其样本矢量集为

(8)

式中vo,i——目标叶型(αo,i)所对应的流场参数

z——样本数

通过式(2)对剔除目标样本矢量的矢量集U进行本征正交分解；通过式(5)进行二乘拟合，最后可由式(4)对式(8)中的目标叶型流场数据vo,i进行重构。预测流场与CFD分析流场对比及其误差分别如图8～13所示。

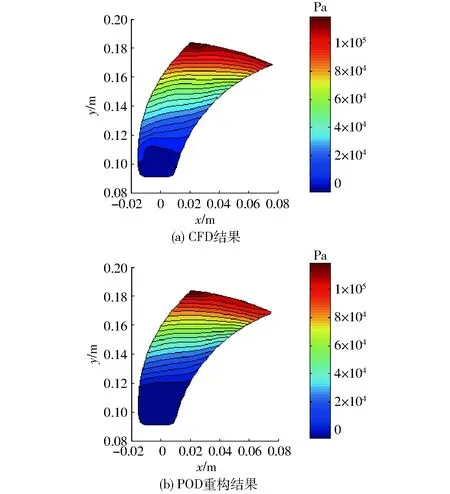
图8 CFD与POD重构的压力场分布Fig.8 Pressure distributions of CFD and POD

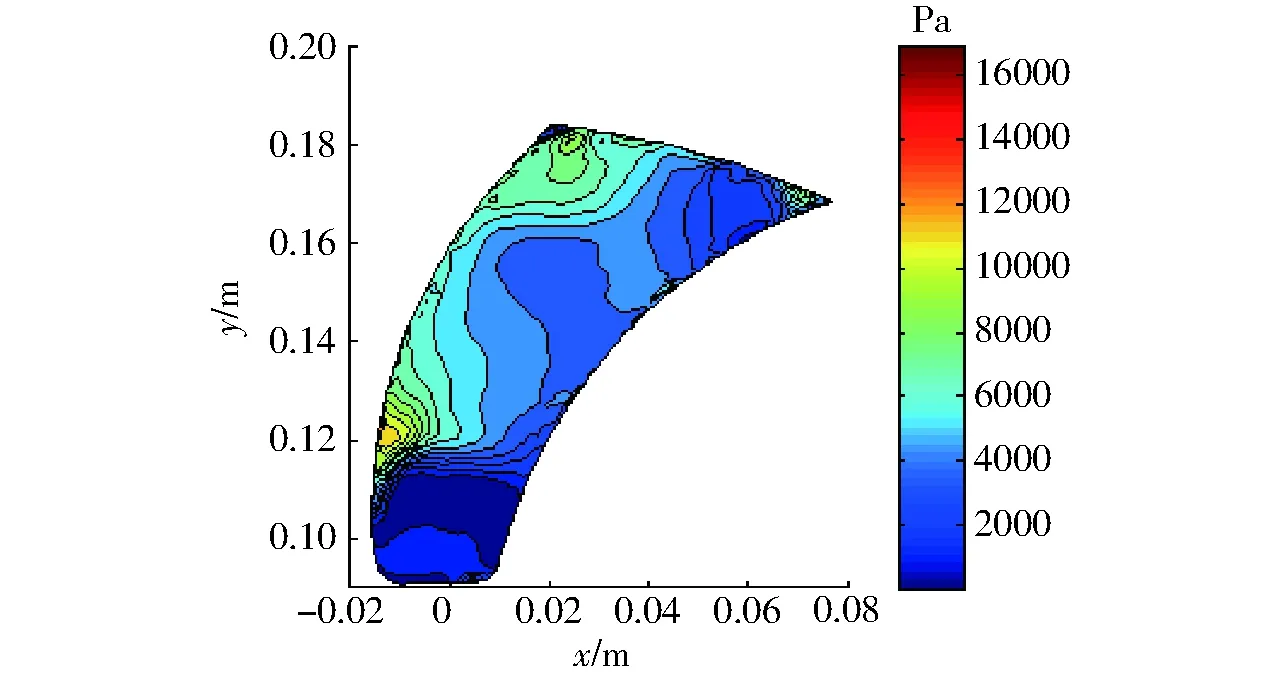
图9 压力场误差分布Fig.9 Distribution of pressure errors

图8为单个叶轮内流道的压力场预测结果与CFD对比，由图可以看出POD预测出的压力场与其CFD分析结果基本一致，从叶轮的轮毂到轮缘压力逐渐增大，在叶片工作面出口附近压力最高。图9为压力预测误差(pCFD-pPOD)的分布情况，可以看出除在气液交界面的叶片工作面附近出现一个较高的局部误差(约10 000 Pa左右)外，整个叶轮内流道的预测误差基本在2 000～4 000 Pa左右,该值相对于叶轮出口平均压力的相对误差为1.7%～3.4%。

图10 CFD与POD重构的体积分数分布Fig.10 Volume fraction distributions of POD and CFD

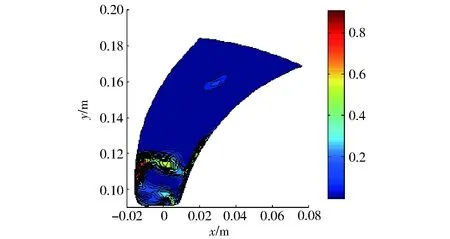
图11 体积分数误差分布Fig.11 Distribution of volume fraction errors

图10为单个叶轮内流道的气液相态的预测结果与CFD结果的对比(α=1为液相，α=0为气相)，可以看出POD方法能较为精确地重构其气液分解面的形状，而且还重构了叶轮中心的一个微小气泡。从图11的误差分布可以看出，除在气液交界面附近的相态有一定误差外，其余整个叶轮流道的相态体积分数误差平均约为0.013。

图12为单个叶轮内流道相对速度场的重构结果与CFD结果的对比，可以看出POD方法精确地重构出了原叶轮内相对速度场的分布特征，在叶片背面靠近出口处、气液交界面靠近叶片的工作面附近等几个局部的高速区域都被POD方法重构出来。图13为重构速度场与CFD速度场间的误差，重构速度场误差的分布与压力场重构误差分布相似，除在气液交界面及叶片出口的工作面附近存在一定的误差外，其余叶轮内大部分区域的相对速度误差在0.2 m/s左右。

图12 CFD与POD重构的速度场分布Fig.12 Velocity distributions of POD and CFD

图13 速度场误差分布Fig.13 Distribution of velocity errors

所提出的POD方法可以精确地实现对液环泵内单个叶轮流道的复杂气液两相流场的重构，对其他叶轮流道流场及壳体流场的重构方法完全一样。该方法可以作为代理模型用于对液环泵优化过程中流场的预估，减少对复杂流场的CFD模拟次数，大大提高了复杂流动优化的速度。

5 结论

(1)提出采用本征正交分解法，对液环泵内的多相流场进行重构分析。对由叶型控制参数及流场参数构成的样本矢量集分解为正交基的线性表示，由最小二乘法拟合目标叶型在该正交基上的各个系数，可以得到目标叶型所对应的各流场参数。

(2)从对2BE-203型液环泵单个叶轮流道内的气液两相流的重构结果看，POD方法能精确地重构出其压力场、速度场及相态场分布的结构特征，除在气液交界面处有一定误差外，整个叶轮内压力的平均相对误差为1.7%～3.4%，相态体积分数平均误差约为0.013，相对速度误差平均值为0.2 m/s。

(3)算例计算结果表明所提出的POD方法能够精确地对液环泵内多相流场进行精确的重构，可以作为代理模型用于流体机械优化设计中对流场的预估，大大减少了优化设计过程中流场的计算量。

1 RAIZMAN I A, MATS É B. Experimental investigation of the velocity field in a liquid ring vacuum-pump[J]. Chemical and Petroleum Engineering, 1972, 8(2): 134-137.

2 KAKUDA K, USHIYAMA Y, OBARA S, et al. Flow simulations in a liquid ring pump using a particle method[J]. CMES, 2010, 66(3): 215-226.

3 TETERYUKOV V I. Effect of body shape on performance of water-ring vacuum pumps[J]. Chemical and Petroleum Engineering, 1966, 2(8): 511-513.

4 黄苗苗, 李国君, 匡晓峰. 水环真空泵内部气液两相流动的数值分析[J].船舶力学,2011,15(7):722-729. HUANG Miaomiao, LI Guojun, KUANG Xiaofeng. Numerical simulation of the gas-liquid tow-phase flow in water-ring vacuum pump[J]. Journal of Ship Mechanics,2011,15(7): 722-729. (in Chinese)

5 黄思, 阮志勇, 邓庆健,等. 液环真空泵内气液两相流动的数值分析[J].真空,2009,46(2):49-52. HUANG Si,RUAN Zhiyong,DENG Qingjian, et al. Numerical analysis of gas-liquid tow-phase flow in liquid-ring vacuum pump[J]. Vacuum, 2009, 46(2): 49-52. (in Chinese)

6 张人会，郭广强，杨军虎,等. 液环泵内部气液两相流动及其性能分析[J/OL].农业机械学报, 2014, 45(12):99-103. http:∥www.j-csam.org/jcsam/ch/reader/view_abstract.aspx?file_no=20141216&flag=1.DOI:10.6041/j.issn.1000-1298.2014.12.016. ZHANG Renhui, GUO Guangqiang, YANG Junhu, et al. Investigation on the inner gas-liquid flow in liquid-ring pump and it’s performance[J/OL]. Transactions of the Chinese Society for Agricultural Machinery, 2014, 45(12):99-103. (in Chinese)

7 MOHAMMADI B, PIRONNEAU O. Applied shape optimization for fluids[M]. Oxford: Oxford University Press, 2010.

8 张人会，郑凯，杨军虎,等. 基于不完全敏感性方法的低比转速离心叶轮优化研究[J].机械工程学报, 2014, 50(4):162-166. ZHANG Renhui, ZHENG Kai, YANG Junhu, et al. The optimization of low specific speed centrifugal impeller based on incomplete sensitivities[J]. Journal of Mechanical Engineering, 2014, 50(4):162-166. (in Chinese)

9 IULIANO E， PEREZ E A. Application of surrogate-based global optimization to aerodynamic design[M]. Berlin: Springer International Publishing, 2016.

10 ANTONY J. Aerodynamic design via control theory[J]. Journal of Scientific Computing, 1988(3): 402-407.

11 MOHAMMADI B, MOLHO J I, SANTIAGO J G. Incomplete sensitives for design of minimal dispersion fluidic channels[J]. Computer Methods in Applied Mechanics and Engineering, 2003, 192: 4131-4145

12 HOTELLING H. Analysis of a complex of statistical variables into principal components[J]. Journal of Education Psychology, 1933, 24: 417-441, 498-520.

13 HOLMES P, LUMLEY J L, BERKOOZ G. Turbulence, coherent structures, dynamical systems and symmetry[M]. Cambridge: Cambridge University Press, 1998.

14 FEENY B F, KAPPAGANTU R. On the physical interpretation of proper orthogonal modes in vibrations[J]. Journal of Sound and Vibration, 1998, 211(4): 607-616.

15 SIROVICH L, KIRBY M. Low-dimensional procedure for the characterization of human faces[J]. Journal of the Optical Society of America, 1987, 4(3): 519-524.

16 RABEN S G, CHARONKO J J, VlACHOS P P. Adaptive gappy proper orthogonal decomposition for particle image velocimetry data reconstruction[J]. Measurement Science and Technology, 2012, 23(2): 25303-25318.

17 BUI-THANH T, DAMODARAN M, WILLCOX K E. Aerodynamic data reconstruction and inverse design using proper orthogonal decomposition[J]. AIAA Journal, 2004, 42(8): 1505-1516.

18 OYAMA A, NONOMURA T, FUJII K. Data mining of Pareto-optimal transonic airfoil shapes using proper orthogonal decomposition[J]. Journal of Aircraft, 2010, 47(5): 1756-1762.

19 白俊强, 邱亚松, 华俊. 改进型Gappy POD翼型反问题方法[J].航空学报,2013,34(4):762-771. BAI Junqiang, QIU Yasong,HUA Jun. Inverse design of airfoil based on Gappy POD method[J]. Acta Aeronautica et Astronautica Sinica, 2013, 34(4): 762-771. (in Chinese)

20 HIRT C W, NICHOLS B D. Volume of fluid(VOF) method for the dynamics of free boundaries[J]. Journal of Computational Physics,1981,39(1): 201-225.

Reconstruction for Gas-Liquid Flow of Liquid-ring Pump Based on Proper Orthogonal Decomposition

ZHANG Renhui1,2WU Hao1YANG Junhu1,2LI Rennian1,2

(1.CollegeofEnergyandPowerEngineering,LanzhouUniversityofTechnology,Lanzhou730050,China2.KeyLaboratoryofFluidMachineryandSystems,GansuProvince,LanzhouUniversityofTechnology,Lanzhou730050,China)

According to the complicated gas-liquid flow in liquid-ring pump, the large amount of calculation, and the difficulty for its optimization design, the flow field reconstitution for the gas-liquid flow of liquid-ring pump based on proper orthogonal decomposition were proposed. The blade was parameterized by Taylor polynomial, and the experiment samples can be designed by introducing small perturbation of the control parameter. The transient gas-liquid flow in liquid-ring pump was simulated by using the VOF model. The snapshot set consisted of the control parameter for the blade shape and the flow field data. According to the geometric similarity of the impeller flow passage and the mesh deformation technology, the flow field data of the similar position of each point were interpolated. The snapshot set can be decomposed as linear combination of orthogonal basis by using proper orthogonal decomposition. The coefficients of the objective blade orthogonal basis were fitted by the least square method. The flow field data of the objective blade were reconstructed. In the calculation case for the type of 2BE-203 liquid-ring pump, the gas-liquid flows of single blade passage were reconstructed, and almost all the flow structures were accurately predicted. The prediction had high accuracy except near the gas-liquid interface. The calculation amount for the multiphase flow field was greatly reduced.

proper orthogonal decomposition; gas-liquid flow; liquid-ring pump; mesh deformation

10.6041/j.issn.1000-1298.2017.06.050

2016-09-22

2016-11-10

国家重点研发计划项目(2016YFB0200901)和国家自然科学基金项目(51469014)

张人会(1977—)，男，副教授，博士生导师，主要从事流体机械内部流动及性能优化研究，E-mail： zhangrh@lut.cn

TH311

A

1000-1298(2017)06-0381-06