基于步幅与体质特征推断年龄的研究

史洪飞, 许宏福

(南京森林警察学院, 江苏南京 51000)

基于步幅与体质特征推断年龄的研究

史洪飞, 许宏福

(南京森林警察学院, 江苏南京 51000)

运用足迹推断年龄是刑事技术领域公认的应用技术，目前国内外足迹专家仅限于对足迹的步态研究，缺少通过步幅特征推断年龄的研究。因此，结合统计学中的Spearman相关知识，将步幅特征、身高、体重与年龄进行相关分析，得出上述因素与年龄在95%的置信水平下显著相关；由于模型存在多重共线性的问题，因此利用主成分分析法，将自变量进行“去相关”的降维，导入模型中进行计算，得出Fi 3个主成分，最后将Fi进行逻辑回归的建模，就能得到推断年龄的3个公式，根据犯罪现场的数据就能推断犯罪嫌疑人的年龄。

步幅特征; 身高年龄； 回归分析

0 引言

目前，足迹特征识别主要应用于公安刑侦领域，在侦查破案过程中显得特别重要[1]。

在国内，早在两千多年前的秦王朝时期，就将“履迹”作为侦破案件的证据[2]。20世纪80年代，公安部牵头组建了“足迹步法定量化检验研究组”，借鉴前人经验，运用数学、测绘、机械、电子等科学的理论知识，经过多年实验研究，创造出了一套系统的足迹步法定量检验方法。但在运用统计学的方法来分析足迹特征方面，目前还比较薄弱[3]。

在国外，足迹研究人员得出了一些非常有意义的结论：在足迹与人身的研究方面，Nakajima等人通过对足迹数据的方向差和位置差等因子的加权分析来识别人身[4]；Robbins等人通过对500名美国人的平面足迹进行尺规测量，得出了足长约为身高的15%的结论[5]。在足迹与生物性方面，Smith研究了足骨与性别、人类种族的分布关系[6]；Kennedy用成年双胞胎的足迹特征差异性来证实这一结论[7]。在步幅特征研究方面，Jasuja等人研究了人体行走时步幅和身高的关系[8]。在足迹特定性分析方面，Kennedy等人采集960个志愿者的墨拓平面足迹，从每个赤足中提取了100个形状特征参数，并通过统计学理论分析了平面赤足足迹对于不同个体之间的可分辨性，但是其部分形状特征的提取仍然需要半人工标定和测量[9]。

国内外关于足迹的研究主要集中在足迹的形态上，通过足迹推断年龄的研究却很少，对足迹步幅特征的研究也存在一定的局限性。基于此，本文将统计学中的相关分析、主成分分析、多元逻辑回归分析等方法与步幅特征结合，进行模型构建，以实现推断年龄的目的。

1 实验部分

1.1 实验器材

印刷油墨；50M*1M的卷纸；吸水海绵；滚筒；直尺；量角器；体重、身高测量器。

1.2 试验方法

1.2.1 样本来源

15～20岁58份；21～30岁57份；30～40岁30份；40岁以上38份，每个人采集10步，取中间4步做为样本。

1.2.2数据测量

将采集的足迹数据进行步长、步宽、步角的测量。每组数据测量3次，取平均数，步幅特征的测量标准见图1。

1.2.3 数据处理方法

使用SPSS10.0软件对数据进行统计处理。

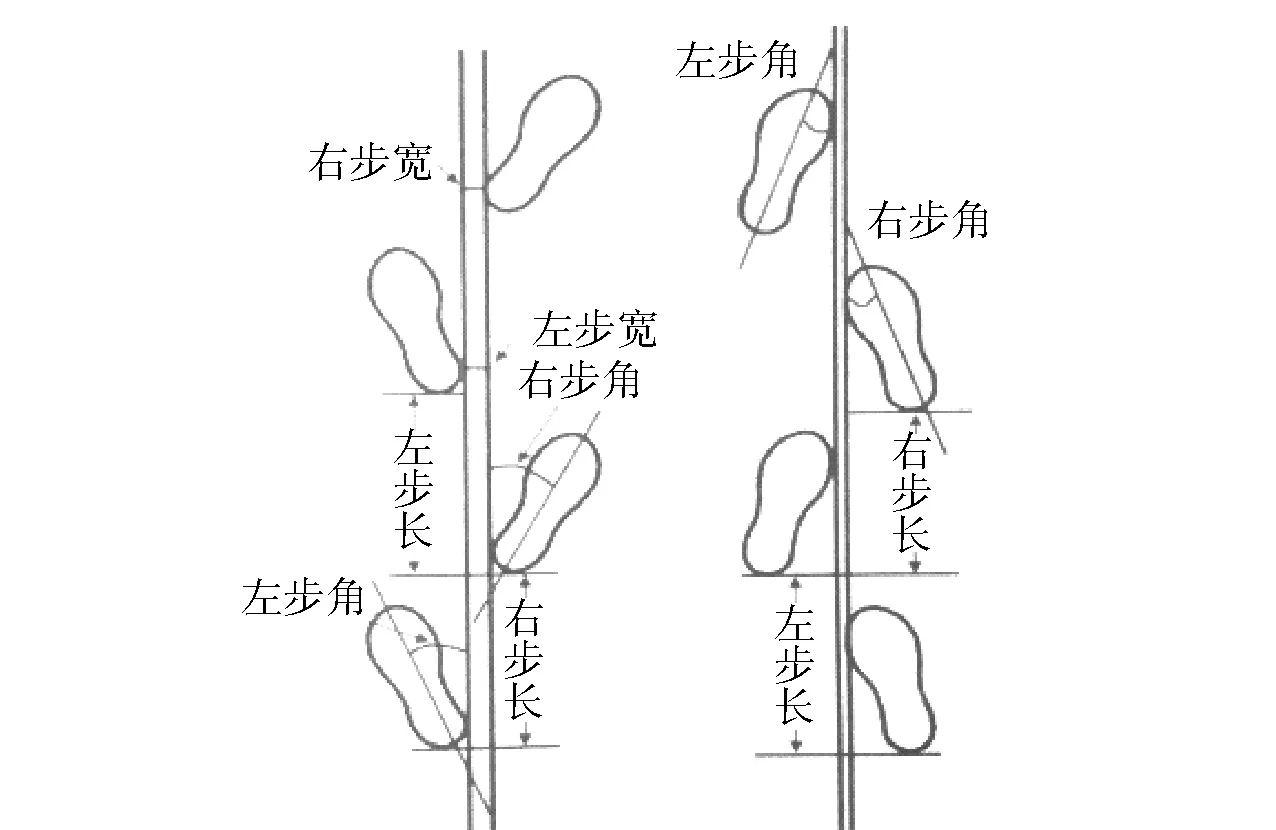
图1

2 实验结果

表1为足迹的部分数据。

3 结果分析与讨论

将采集的足迹、身高、体重、性别与年龄进行相关分析，得出年龄与其他因素的相关关系；考虑模型存在的多重共线性的问题，因此利用主成分分析法，将自变量进行“去相关”的降维，导入模型中进行计算，得出Fi 3个主成分，最后将Fi进行逻辑回归的建模，就能根据足迹推断年龄。

表1 正常行走状态下成趟足迹步幅特征数据

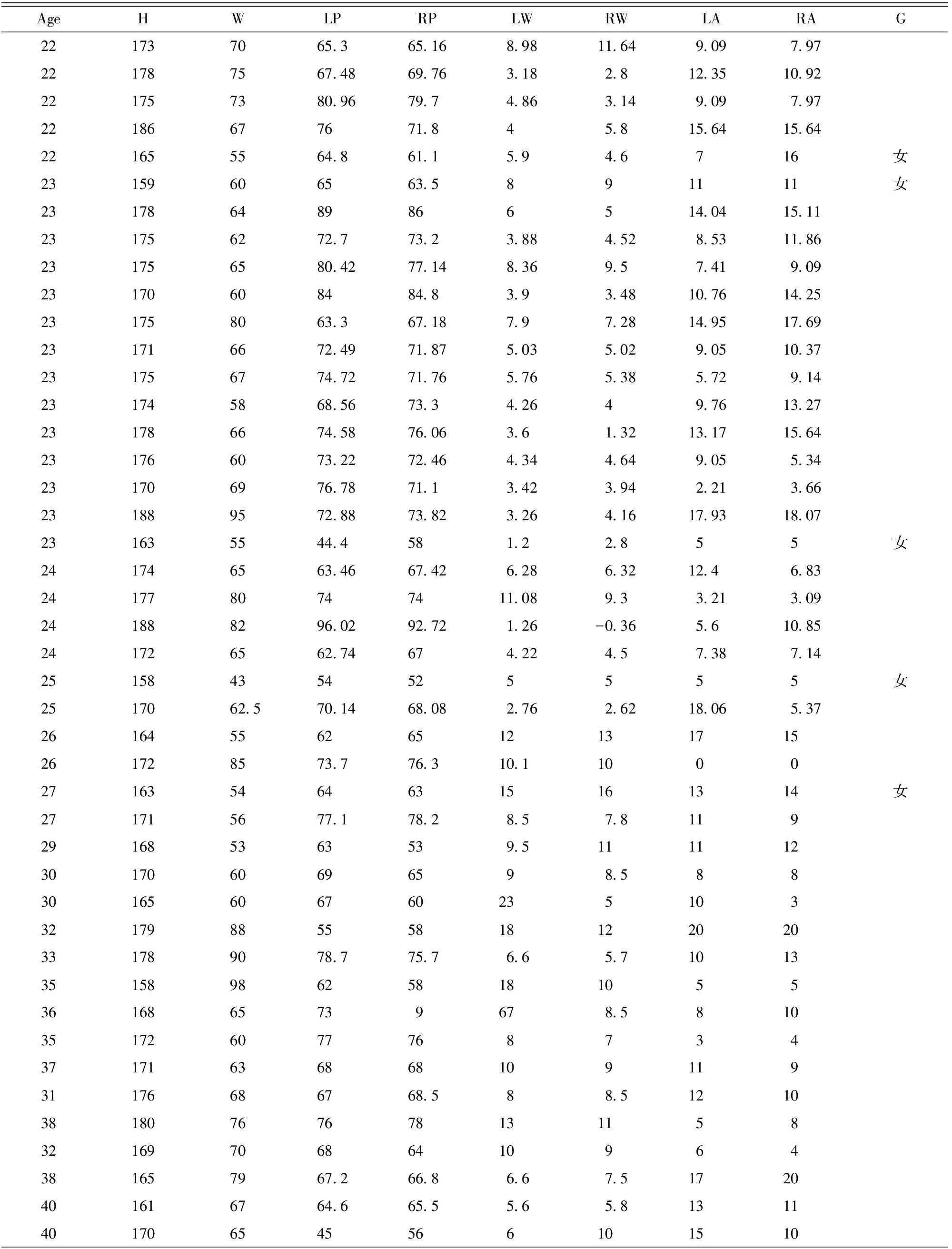
续表1

续表1

注：(1)身高：H，单位：m；体重：W，单位：kg；左步长：Lp，单位：cm；右步长：Rp，单位：cm；左步宽：Lw，单位：cm；右步宽：Rw，单位：cm；左步角：La，单位：°；右步角：Ra，单位：°；性别：G。(2)表中未标注的均为男性。

3.1 相关性分析

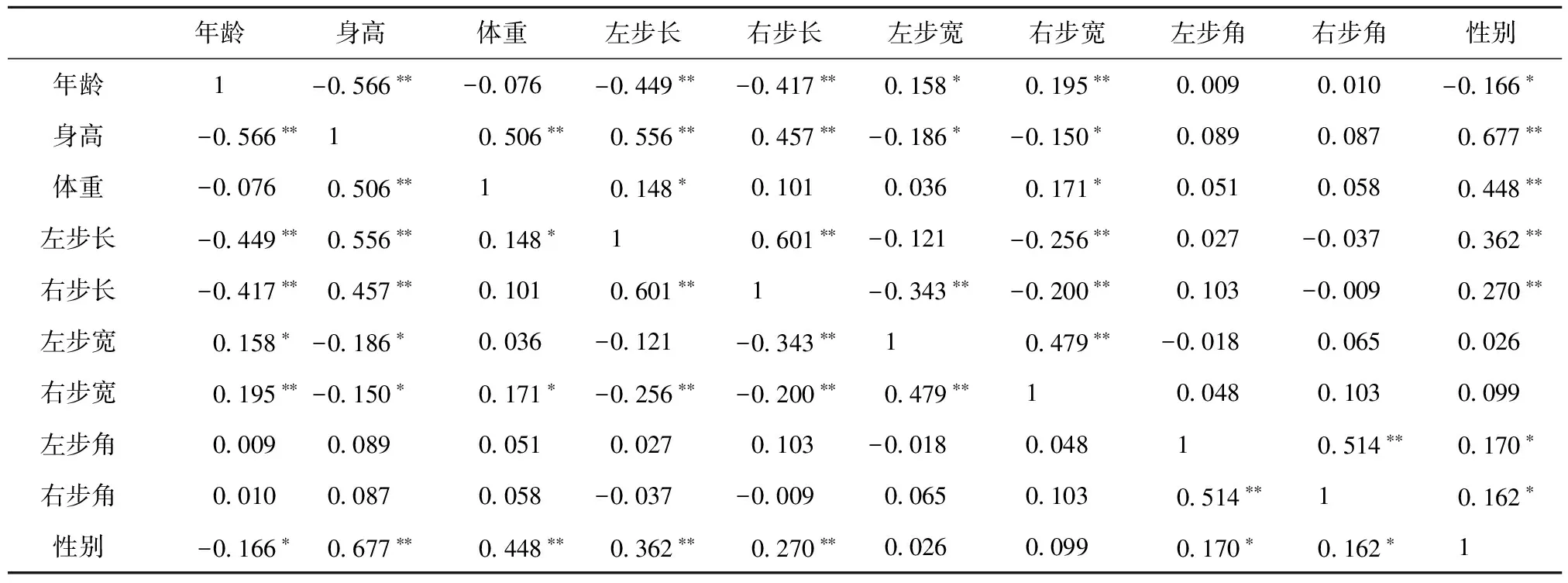
表2 步幅特征、身高、体重、性别与年龄相关性表

**0.在 00.01 水平(双侧)上显著相关；*0.在 00.05 水平(双侧)上显著相关。

从统计学上看，年龄与身高在置信水平为95%的条件下，呈现显著相关的关系，同样可以发现，年龄与性别、身高、体重、左右步长以及左右步宽均呈现显著的相关关系，只有步角在统计学意义上与年龄不相关。因此本研究中排除了步角的影响，以身高、体重、左右步长以及左右步宽作为自变量，年龄作为因变量进行模型的构建。

但是在实际的模型构建过程中，用线性回归的方法计算的是年龄的具体值，由于回归方法本身的原因，年龄值的结果是不精确的，在这样的前提下，对年龄的范围进行预测更加符合实际的工程意义，因此本文考虑将年龄分成3个范围，分别是20岁以下、20～30岁、30岁以上3个阶段，以此作为分类变量，进行逻辑回归。

3.2 主成分分析(Principal Component Analysis，PCA)

逻辑回归的第一步就是进行自变量相关性检验，但是本文中的自变量都是相关的，可进行“去相关性”的降维，然后导入模型进行计算，结果见表3。

表中KMO值接近于1，认为可以进行主成分分析的降维，而Bartlett的球形度也显示显著值为0.00小于0.05，拒绝原假设相关系数矩阵为单位阵，说明变量间存在相关关系，即适合做因子分析。

从表4提取一列，可以观察到不同变量的共同度较高，变量中的大部分信息能被成分所提取，这更加说明主成分分析是有效的。

表3 KMO和Bartlett的检验

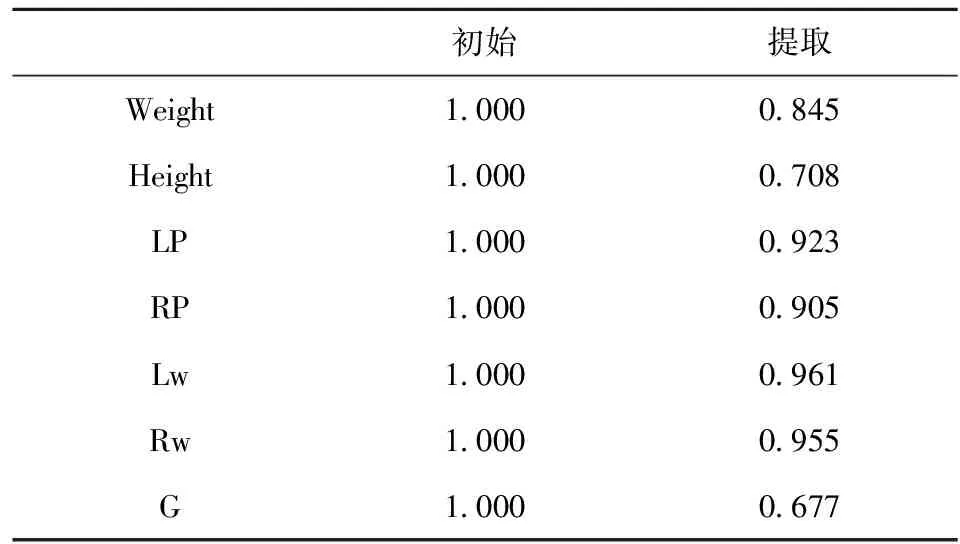
表4 公因子方差

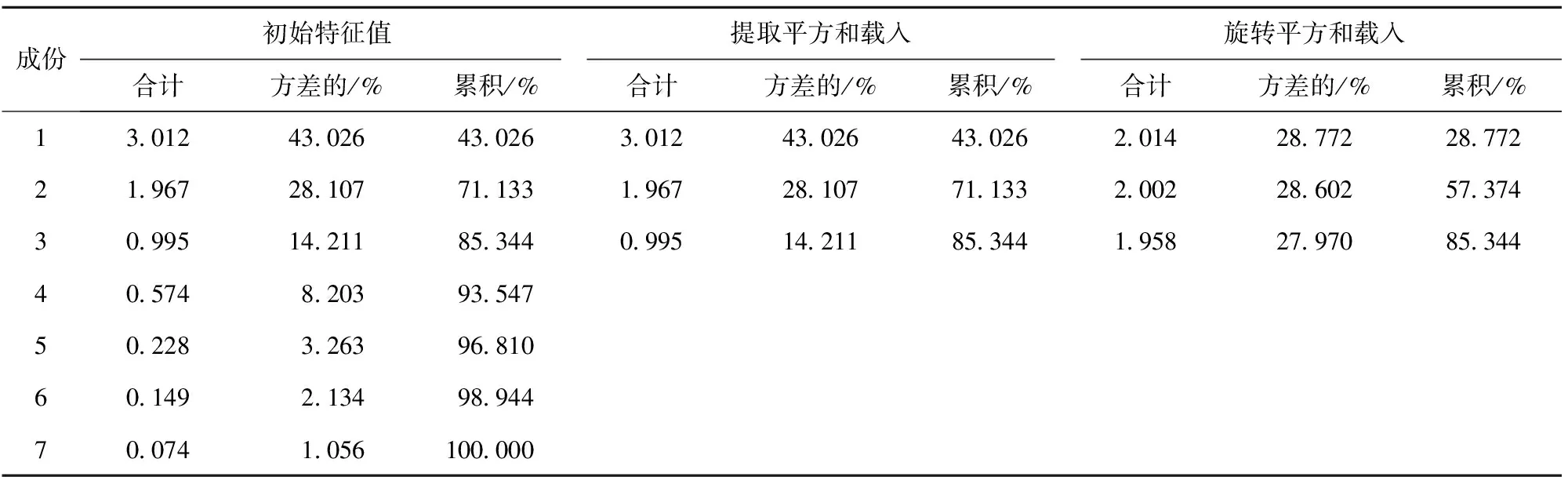
表5 解释的总方差

图2

从表5中可以看出，前3个成分的特征值都大于1或者近似的等于1，且方差累计率达到了85.34%>85%，因此提取前3个成分作为主成分，进行后续的计算，另外从下图3.5的碎石图中也可以看出前3个成分处于非常陡峭的斜率上，第四个成分变缓，基于以上的原因就可以取前3个成分作为主成分进行分析。

经过以上的分析计算，可以将最初的相关变量用3个成分进行表达，进而将其作为逻辑回归的新的自变量。3个主成分可以由之前的变量进行表达：

(1) F1=0.793*x1+0.833*x2+0.203*x3+0.179*x4-0.008*x5+0.058*x6+0.784*x7

(2) F2=0.435*x1-0.020*x2+0.935*x3+0.922*x4-0.105*x5-0.121*x6+0.249*x7

(3) F3=-0.162*x1+0.115*x2-0.083*x3-0.153*x4+0.975*x5+0.968*x6+0.029*x7

以上x1～x7分别是身高、体重、左脚长、右脚长、左脚宽、右脚宽以及性别，每一个变量都是经过标准化后进行叠加处理的。

3.3 多元逻辑回归分析

基于以上的主成分分析，对F1、F2以及F3进行处理，采用多元逻辑回归的方法构建模型。

表6是整个逻辑回归的拟合效果，在95%的置信水平下，模型的显著水平为0.000<0.05，因此在统计学上认为，该模型是成立的。

表7中表示的不同变量在模型中的显著性水平，在95%置信水平下认为不同的自变量在模型中产生了显著的影响，也就是模型的3个主成分可以较充分地表达整个模型。

表6 模型拟合信息

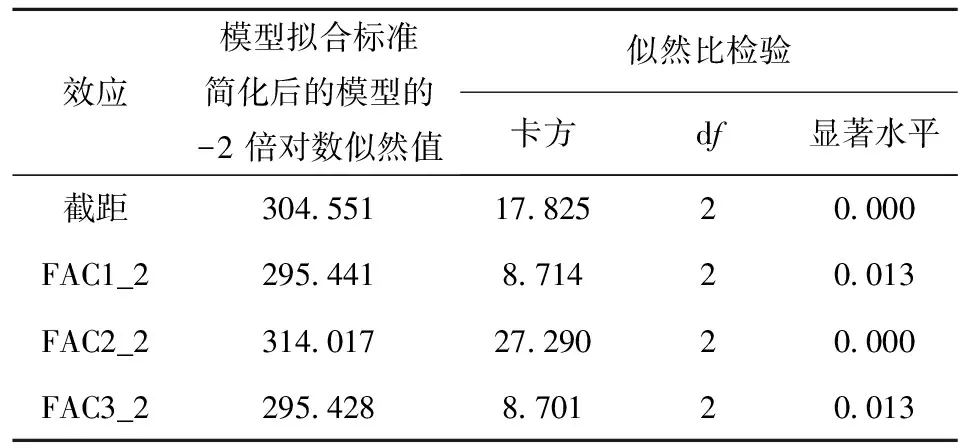
表7 似然比检验

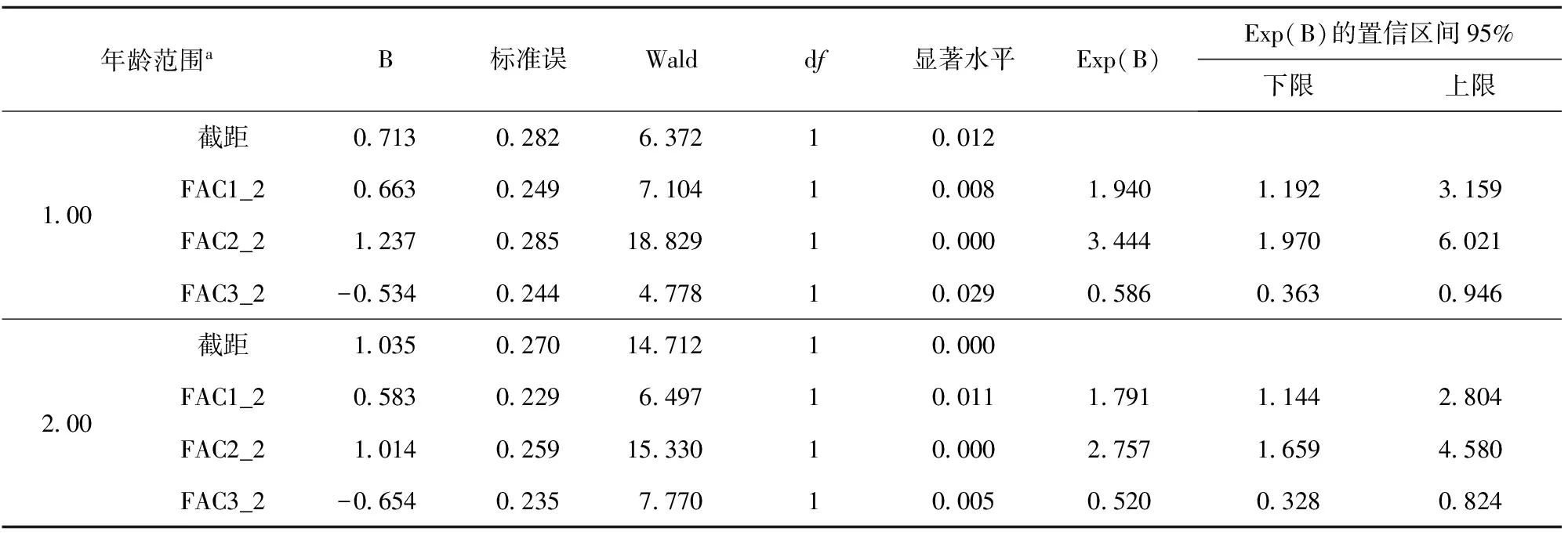
表8 参数估计

表8中给出了不同的自变量的相应的系数，借助该系数可以完成整个年龄推断模型的建立：

(3)P(Y=3)=1-P(Y=1)-P(Y=2)

3.4 讨论

通过以上模型的计算可以算出当Y分别取1,2,3时的概率值，取其中最大的就是对应的种类。通过对以上模型的建立，就可以完成足迹对年龄范围的预测。

本次实验可知，步幅特征、身高、体重等成分与年龄存在显著相关性，通过建立模型，就可以实现足迹对年龄范围的预测。但是本文中所提出的模型与之前的模型不同，针对不同的地区，模型要随之变化，因此首先是要建立一个所在地区的信息库(适宜大小)，根据库中的信息进行模型的建立，具体的流程就是：

(1)采集足迹以及体重、身高、性别的信息，相关性分析筛除变量，主成分分析处理自变量进而去相关性，根据主成分建立逻辑回归的方程。

(2)当模型建立完成，以后就可以根据这些的基础的信息对年龄范围进行预测。

本研究也存在不足之处，在运用步幅特征推断年龄时，引入了身高体重这两个成分，然而在侦查实践过程中，身高体重的数据不能直接获得。因此在接下来的研究中还要进一步深入：

(1)对模型进行改进，转换模型的条件，研究新的方法；

(2)通过对不同年龄阶段足迹数据库的完善，将年龄阶段的分级进行细化，进而确定足迹年龄的具体范围，提高足迹推断年龄的准确度。

4 结语

本次实验可知，在步幅特征、身高、体重等成分与年龄存在95%的相关性时，其Exp(B)置信区间可达到95%上下限，通过建立模型，就可以通过足迹对年龄的范围进行预测，从而提高侦查破案的速度。

[1] 黄雨婷 ，姚宇端. 论足迹在刑事案件侦查中的重要性[J]. 法制观点，2015(1)：115.

[2] 王清祥，韩均良，郑德才，等. 足迹步法定量化检验[M]. 北京：中国人民公安大学出版社，1992.

[3] 李磊，童莉，平西建. 平面足迹形状分析[J]. 计算机辅助设计与图形学学报，2006，18(7):976-981.

[4] SMITH S L.Attribution of foot bones to sex and population groups [J] . Journal of Forensic Science,1997,42(2):186-195.

[5] ROBBINS L M. The individuality of human footprint[J].Journal of Forensic Science,1978,23(4):778-785.

[6] NAKAJIMA K, MIZAKAMI Y, TANAKA K et. Al. Footprintbased personal recognition [J] .IEEE.Transactions on Biomedica Engineering,2000,47(11):1534-1537.

[7] KENNEDY R B.Uniqueness of bare beet and its use as apossible mens of identification [J]. Forensic Science Tnternation,1996,82(1):81-87.

[8] JASUJA O P. HARBHAJAN S, ANUPAMA K. Estimation of stature from stride Length while walking Fast[]. Forensic science International,1997,86(3):181-186.

[9] KENNDY R B, PRESSMAN I S, CHEN S P, et al. Statistical analysis of barefoot impressions[J] . Journal of Forensic Seiences,2003,48(1)：55-63.

(责任编辑 陈小明)

史洪飞(1981—)，男，山东曹县人，讲师。研究方向为刑事科学技术痕迹与化验。

D919.4