弹道导弹飞行时间偏差修正方法*
李泽秀,朱昱,鲜勇,张大巧
(火箭军工程大学,陕西 西安 710025)
弹道导弹飞行时间偏差修正方法*
李泽秀,朱昱,鲜勇,张大巧
(火箭军工程大学,陕西 西安 710025)
为实现弹道导弹精确时间协同作战,需要对出现的飞行时间偏差进行控制。根据摄动理论将飞行时间偏差在末修段预定点展开成速度和位置的线性形式,建立修正飞行时间偏差所需速度增量方程组,求出修正所需速度增量、推力作用时间和方向,利用末修发动机对飞行时间偏差进行修正。仿真计算表明:该方法可有效修正导弹飞行时间偏差。
弹道导弹;时间协同;摄动制导;飞行时间偏差;修正;末修
0 引言
在弹道导弹协同作战中,常采用集群射击的方式对敌重要目标进行打击,目的是使各导弹能够在同一时刻到达目标以提高导弹的突防能力和打击效果[1-3]。实现多枚导弹同时到达同一目标通常有2种方式:一种是在发射前装订好共同的到达目标时间,计算好诸元再进行独立导引和控制飞行。另一种是各导弹在飞行过程中基于通信网络进行时间协同,调整到达目标的时间[4]。弹道式导弹的制导方式通常是三维制导,较少考虑时间的因素,面对性能日益完善的反导系统和导弹协同作战需要,三维制导难以满足现实要求。而采用“三维空间+时间”的四维精确制导能够控制各导弹几乎同时到达目标从而实施饱和攻击、集群突防和协同作战[5]。弹道式导弹在进行饱和攻击、集群突防和协同作战时通常采用地面计算好的标准弹道飞行时间进行发射时间规划以达到同时攻击的目的,这就要求导弹在飞行过程中严格按标准弹道飞行才能实现按预定时间到达目标。但导弹自身状态及飞行过程中的环境与标准弹道不可避免的存在差异和各种干扰,这必将导致弹道导弹实际飞行时间与预定飞行时间存在偏差,从而影响饱和攻击的时间饱和度及协同作战效果。
为提高弹道导弹时间协同作战能力,需要对导弹的飞行时间进行精确控制,对出现的飞行时间偏差进行修正。在导弹飞行中,影响导弹飞行时间的主要因素集中在大推力助推段,因此在末修段飞行中,在预定修正点根据时间偏导数计算飞行时间偏差,利用末修发动机对飞行时间偏差进行修正可确保导弹攻击时间上的协同[6-7]。本文基于摄动理论对导弹飞行时间偏差修正进行研究。
1 基本思路
基于摄动理论思想[8],在导弹飞行末修段的预定修正点,在地面计算好导弹飞行时间对速度和位置的偏导数。当导弹飞至预定修正点时求出导弹实际飞行的速度和位置与标准弹道的等时偏差,根据飞行时间偏差的线性展开式计算导弹飞行时间偏差。为修正导弹到达目标的飞行时间偏差,由飞行时间偏差的线性展开式和落点偏差线性展开式求解修正飞行时间偏差所需的速度增量,这样计算得到的速度增量在修正飞行时间偏差的同时使其引起的落点偏差为0,最后根据末修动力计算推力作用时间和方向进行修正。
2 飞行时间偏差计算
导弹在实际飞行中,由于自身状态、飞行环境中各种干扰如干扰风的存在,将导致导弹实际飞行弹道与标准弹道存在偏差,而弹道式导弹的制导没有考虑飞行时间的精确控制,这必然导致导弹的飞行时间与预定飞行时间出现偏差。飞行时间偏差的产生主要是在导弹的主动段,当导弹实际飞行弹道与标准弹道偏差不大时,可利用摄动思想,即小扰动理论,将飞行时间偏差Δt在标准弹道飞行时间附近展开,选取变化率大的位置进行修正[9]。
由椭圆弹道理论可知,导弹的飞行时间tm是当前飞行时刻tk的速度(vxa,vya,vza)及位置(xa,ya,za)的函数,则有
(1)
式中:Δvia,Δia(i=x,y,z)是惯性坐标系下导弹的速度和位置;tc是以速度(vxa,vya,vza)和位置(xa,ya,za)关机的被动段飞行时间。
(2)
由于弹道导弹的飞行时间计算难以用明确的解析表达式表示,且用弹道方法计算飞行时间精度高,因此本文将导弹飞行时间表示为相关参数的函数形式,基于标准弹道用时间对速度和位置的偏导数计算飞行时间偏差。

(3)
式中:
(4)
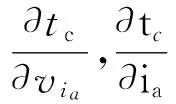
3 飞行时间偏差修正点选择分析
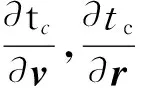

图1 飞行时间对速度的偏导数随飞行时间变化图Fig.1 Flight time variation of partial derivative of flight time to velocity

图2 飞行时间对位置的偏导数随飞行时间变化图Fig.2 Flight time variation of partial derivative of flight time to position
4 飞行时间偏差修正
4.1 偏差修正量计算

(5)
为修正飞行时间偏差ΔTi,设所需的速度增量为Δvnja(j=x,y,z),施加速度增量所导致的位置增量为Δjna(j=x,y,z)。要使ΔTi=0,速度增量和位置增量要满足:
(6)

(7)
(8)
要修正导弹的飞行时间偏差,同时又要使修正不产生新的落点偏差,则修正所需的速度增量要满足式(6)的同时使得ΔL=0,ΔH=0,即满足下列方程组:
(9)

(10)
求解上述方程组可得
(11)
(12)
设速度增量Δvna在Oxaya面内的投影与Oxa轴的夹角为φa,Δvna与Oxaya面的夹角为ψa[13],其中Oxayaza为惯性系,则
(13)
(14)
φa,ψa在发射系中为φx,ψx,则
(15)
(16)
设末修级的推力为Fm,末修初始质量为mm,施加修正飞行时间偏差所需的速度增量的时间为ΔtF[14],则
(17)
(18)
(19)
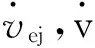
(20)
速度增量为
(21)
为简化计算,在此设加速度为常量,由式(11),(12),(15)~(21)可求出ΔtF为
(22)
由式(20),(22)可求得速度增量引起的位置增量为
(23)

(24)
再次求解式(9)得到新的修正飞行时间偏差所需的速度增量为
(25)

4.2 修正量预测校正

飞行时间修正偏差修正流程:
步骤1:由式(5)求得ti时刻飞行时间偏差ΔTi;



步骤8:将位置增量Δx″na,Δy″na,Δz″na带入式(9)求出修正飞行时间偏差所需速度增量Δv‴nxa,Δv‴nya,Δv‴nza;
步骤9:重复步骤3至步骤6即可求出修正飞行时间偏差ΔTi发动机推力作用时间Δt″F和推力方向φ″a,ψ″a。
步骤10:重复步骤1至步骤9,当飞行时间偏差ΔTi+k<ε(ε为预设修正精度)或末修发动机已工作时间tj=tmax(tmax为末修发动机最大工作时间)时,飞行时间偏差修正结束。
5 仿真分析
本文以一典型弹道进行仿真,末修级的推力为Fm=1 050 N,末修初始质量为mm=1 000 kg,标准弹道飞行时间为810.24 s,在标准弹道基础上分别添加飞行时间偏差-1 s和-3 s,记为偏差弹道1和偏差弹道2,其弹道参数如表1所示。在末修段利用本文方法按标准弹道飞行时间进行飞行时间偏差修正,仿真结果如表2所示,各弹道参数变化如图3~5所示。

图3 偏差弹道2末修段导弹速度随时间的变化曲线图Fig.3 Time variable graph of missile velocity in terminalcorrection phase of deviation ballistic 2
从仿真结果表1,2及图3~5可以看出,运用上述方法能够准确计算导弹飞行时间偏差并有效修正此偏差,修正后导弹能按标准弹道飞行时间到达目标,且飞行时间偏差修正后导弹的落点精度得到了一定提高,说明此方法修正较小范围的时间偏差是可行的。

表1 飞行时间偏差修正前的弹道参数Table 1 Ballistic parameters before flight time deviation correction

表2 飞行时间偏差修正仿真结果Table 2 Simulation results of flight time deviation correction

图4 偏差弹道2末修段弹道倾角随时间的变化曲线图Fig.4 Time variable graph of trajectory inclination angle in terminal correction phase of deviation ballistic 2

图5 偏差弹道2飞行时间偏差修正前后及标准弹道曲线图Fig.5 Graphs of ballistic of standard ballistic and deviation ballistic 2 of flight time deviation before and after correction
6 结束语
本文基于摄动理论,利用导弹飞行时间对速度和位置的偏导数,计算导弹飞行时间偏差,同时计算利用末修发动机进行飞行时间偏差修正所需的速度增量、推力作用时间和方向。为使飞行时间偏差修正不影响导弹落点,在计算修正偏差所需的速度增量时加入ΔL(Δv)=0,ΔH(Δv)=0的约束。通过仿真验算说明该方法能够有效修正一定大小的飞行时间偏差同时对导弹落点影响较小,对导弹协同作战研究具有重要参考意义。
[1] 王辉,田劲松,张莉英.基于飞行时间的弹道导弹火力控制[J].火力指挥与控制,2005,30(2):85-91. WANG Hui,TIAN jin-song,ZHANG Li-ying.Research on Firepower Control of Ballistic Missile Base on Flight Time[J].Fire Control and Command Control,2015,30(2):85-91.
[2] 杨雪冬,朱蕊蘋,李君龙.交会时间可控的多子弹协同制导方法[J].现代防御技术,2013,41(1):59-63. YANG Xue-dong,ZHU Rui-ping,LI Jun-long.Submunitions Cooperative Guidance Method of Controllable Rendezvous Time[J].Modern Defence Technology,2013,41(1):59-63.
[3] 王晓芳,洪鑫,林海.一种控制多弹协同攻击时间和攻击角度的方法[J].弹道学报,2012,24(2):1-5. WANG Xiao-fang,HONG Xin,LIN Hai.A Method of Controlling Impact Time and Impact Angle of Multiple-missiles Cooperative Combat[J].Journal of Ballistics,2012,24(2):1-5.
[4] 张友安,王星亮,吴华丽,等.带攻击时间约束的导引律综述[J].海军航空工程学院学报,2015,30(4):301-309. ZHANG You-an,WANG Xing-liang,WU Hua-li,et al.Overview of Guidance Law with Impact Time Constraint[J].Journal of Naval Aeronautical and Astronautical University,2015,30(4):301-309.
[5] 王晓芳,郑艺裕,林海.导弹协同作战四维制导与控制一体化设计方法[J].系统工程与电子技术,2015,37(4):874-881. WANG Xiao-fang,ZHENG Yi-yu,LIN Hai.4D Integrated Guidance and Control Law for Missiles Cooperative Encasement[J].Systems Engineering and Electronics,2015,37(4):874-881.
[6] 马丹山,王明海.弹道导弹小推力落点修正[J].上海航天,2008(3):16-22. MA Dan-shan,WANG Ming-hai.Study on Correction of the Ballistic Missile’s Falling Point with Little Thruster[J].Aerospace Shanghai,2008(3):16-22.
[7] 郭跃,刘新学,蒋鸣.基于在线修正弹道模板的主动段弹道跟踪方法[J].弹道学报,2014,26(3):17-22. GUO Yue,LIU Xin-xue,JIANG Ming.Method of Tracking Boost Phase Trajectory Based on Online-Modified Trajectory Profile[J].Journal of Ballistics,2014,26(3):17-22.
[8] 张毅,肖龙旭,王顺宏.弹道导弹弹道学[M].长沙:国防科技大学出版社,2005:115-119. ZHANG Yi,XIAO Long-xu,WANG Shun-hong.Ballistic Missile Ballistics[M].Changsha:National University of Defense Technology Press,2005:196-199.
[9] 赵炤,周经伦,罗鹏程.打击时敏目标作战火力打击时间建模方法及其应用[J].海军工程大学学报,2010,22(6):42-46. ZHAO Zhao,ZHOU Jing-lun,LUO Peng-cheng.Modeling Method on Striking-Time of Operation for Time-Sensitive-Target-Striking[J].Journal of Naval University of Engineering,2010,22(6):42-46.
[10] 肖龙旭,王顺宏,魏诗卉.地地弹道导弹制导技术与命中精度[M].北京:国防工业出版社,2009:130-135. XIAO Long-xu,WANG Shun-hong,WEI Shi-hui.Ground to Ground Ballistic Missile Guidance Technology and Hit Accuracy [M].Beijing:National Defense Industry Press,2009:130-135.
[11] 马瑞萍,许化龙,肖凡.摄动制导诸元计算的一种模糊控制方法[J].航天控制,2011,29(2):23-30. MA Rui-ping,XU Hua-long,XIAO Fan.Fuzzy Control Method of Computing Disturbance Guidance Firing Data[J].Aerospace Control,2011,29(2):23-30.
[12] 鲜勇,肖龙旭,李刚.组合制导弹道导弹无依托快速发射技术研究[J].宇航学报,2010,31(8):1915-1919. XIAN Yong,XIAO Long-xu,LI Gang.Research on Offhand Fast Launch Technique for Integrated Guidance Ballistic Missile[J].Journal of Astronautics,2010,31(8):1915-1919.
[13] 马丹山,刘新学,王力纲.闭路制导推力方向研究[J].飞行力学,2005,23(3):64-66. MA Dan-shan,LIU Xin-xue,WAND Li-gang.An Approach to Close-Loop Guidance Thruster Direction[J].Flight Dynamics,2005,23(3):64-66.
[14] 田再克,杨锁昌,冯德龙,等.弹道修正弹脉冲发动机作用角度优化研究[J].弹箭与制导学报,2014,34(2):105-108. TIAN Zai-ke YANG Suo-chang,FENG De-long,et al.The Research on Pulse Jet Action Angle Optimization of Trajectory Correction Projectile [J].Journal of Projectiles,Rockets,Missiles and Guidance,2014,34(2):105-108.
[15] 邵雷,雷虎民,段朝阳,等.基于误差修正的直接力/气动力双层姿态控制设计[J].固体火箭技术,2014,37(6):769-780. SHAO Lei,LEI Hu-min,DUAN Chao-yang,et al.Blended Attitude Control Method with Lateral Thrust and Aerodynamic Force Based on Error Compensation[J].Jourrnal of Solid Rocket Technology,2014,37(6):769-780.
[16] 曾宪法,王洁瑶,王小虎.基于能量和解析预测校正的滑翔制导[J].系统工程与电子技术,2013,35(12):2582-2588. ZENG Xian-fa,WANG Jie-yao,WANG Xiao-hu.Gliding Guidance Based on Energy and Analytical Predictor-Corrector[J].Systems Engineering and Electronics,2013,35(12):2582-2588.
[17] 党露,和兴锁,徐卫昌.固定时间轨道拦截的制导方法研究[J].飞行力学,2014,32(3):266-269. DANG Lu,HE Xing-suo,XU Wei-chang.Guidance for Time-Fixed Orbital Interception[J].Flight Dynamics,2014,32(3):266-269.
Method for Correcting Flight Time Deviation of Ballistic Missile
LI Ze-xiu,ZHU Yu,XIAN Yong,ZHANG Da-qiao
(Rocket Force University of Engineering,Shaanxi Xi’an 710025,China)
In order to realize the coordinated operation of ballistic missile, it is necessary to control the flight time deviation. According to perturbation theory, the flight time deviation is expanded into the linear form of velocity and position at the scheduled point of terminal correction phase, and the required velocity increment equations are established to correct the flight time deviation. The flight time deviation is modified by terminal correction thruster based on the required velocity increment, thrust time and direction which are derived from the equations. The simulation results show that the method can effectively correct the missile flight time deviation.
ballistic missile;time cooperative;perturbation guidance;flight time deviation;correct;terminal correction
2016-07-19;
2016-08-30
李泽秀(1988-),男,云南玉溪人。硕士生,研究方向为主要从事飞行器动力学与制导研究。
通信地址:710025 陕西省西安市灞桥区洪庆镇同心路2号4502分队(杨晓) E-mail:lizexiu0@163.com
10.3969/j.issn.1009-086x.2017.03.009
TJ761.3;TJ765
A
1009-086X(2017)-03-0054-07

