基于D-H方法建立抛光机器人的运动学模型

宋修洋，陈劲杰，余 洁

(上海理工大学 机械工程学院，上海 200093)



基于D-H方法建立抛光机器人的运动学模型

宋修洋，陈劲杰，余 洁

(上海理工大学 机械工程学院，上海 200093)

为提高自由曲面表面工艺品质，提出用机器人运动模型来规划其各关节的加工路径。基于D-H表示法的思想，求解机器人正逆运动学方程来判断末端执行器的运动轨迹，从而进行机器人的运动学仿真。使机器人末端执行器实现字符"ME"轨迹，展示具体应用方法,得出了机器人的运动轨迹，为自由曲面自动化抛光处理更加智能高效提供了理论依据。

D-H表示法；运动学模型；正逆运动学方程；有效性验证

现代工业产品复杂层度在不断增加，新的加工制造方法层出不穷，导致了产品的生产工艺路线的可行解也成指数方式增长。为了与这种新的发展形势相适应，合理规划机器人运动路径是保证零件加工质量和效率的关键步骤，也是机器人抛光系统设计的重要一步。

1 机器人的空间描述

(1)

式中，Px、Py和Pz分别为该点的在x轴、y轴和z轴方向的空间坐标。

获取了物体的任意点位置后，还需要得到该物体的姿态信息方可进行运动学分析。假设直角坐标系F与该物体固定相连接，则可通过坐标系F的3个方向的主矢量表示物体对于相对参考系的姿态

(2)

如图1所示，空间物体在任一坐标系中的表示可通过位置矢量和旋转矩阵描述。图中物体与坐标系F0固定连接，坐标系F0的原点为物体的质心，则物体在坐标系F0中可以表示为

(3)

图1 空间物体表示

2 坐标系变换

(4)

式中，dx、dy和dz分别表示局部坐标系在全局坐标系对应坐标轴方向的位移。

旋转角度为θ的坐标系3个方向的变换矩阵分别为

(5)

(6)

(7)

令UP表示点P相对于坐标系U的描述；UTR表示坐标系R相对于坐标系U的变换；RP表示点P相对于坐标系R下的描述，其间的关系为

UP=UTR×RP

(8)

3 六自由度机器人运动学模型

3.1 机器人结构参数

进行仿真分析前要先确定打磨机器人的D-H参数。D-H表示法是1955年，Denavit和Hartenberg提出的，是机器人运动学建模的标准方法[15-16]。采用D-H方法建立机器人运动学模型，则必须在所有关节处建立相对应的局部参考坐标系。所以，对于每一个关节的表示方法如图2所示。

图2 相邻连杆关系的D-H参数

对于刚性连杆，其D-H表示方法主要通过对以下4个参数进行定义：(1)连杆长度ai表示沿xi轴方向Zi-1轴与zi轴之间的距离；(2)连杆扭角αi表示绕xi轴线由zi-1轴到zi轴所旋转的角度；(3)连杆间距di表示沿zi轴方向xi-1轴到xi轴的距离；(4)转角变量θi表示绕zi轴由xi-1轴到xi轴所旋转的角度。本文所设计的机器人三维模型和D-H参数分别如图3和表1所示。

图3 机器人三维模型

连杆转角变量θ°/(°)连杆间距di/mm连杆长度αi/mm连杆扭角αi/(°)转角变量范围1θ101250-180°～180°2θ200-90-15°～180°3θ304160-180°～180°4θ40090-90°～90°5θ50318-90-180°～180°6θ6128090-75°～75°

3.2 机器人正逆运动学方程的解

本文所设计的机器人为6自由度，通过D-H建模方法对每一个连杆建立相应的局部坐标系。如图4所示为机器人处于初始状态下的运动学模型，即各关节的转角分别为0°、-90°、90°、0°、0°和0°。

机器人不同的局部坐标系之间的关系满足一定关系，坐标系{i}与坐标系{i-1}之间的坐标变换矩阵为

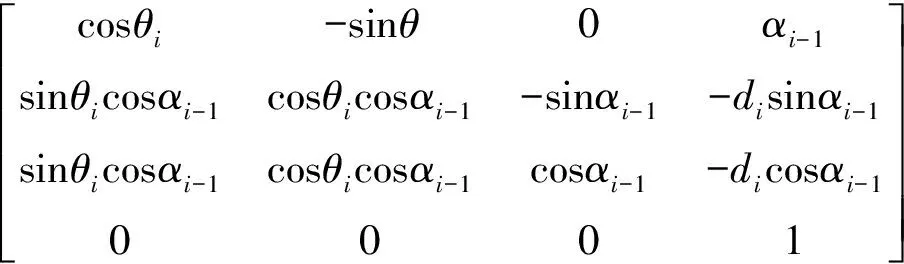
(9)

式中，θi为第i个关节的关节角；di为第i个关节的偏置距离；αi-1为第i-1个连杆的扭角；αi-1为第i-1个连杆的长度。

图4 6自由度机器人运动学模型

由式(9)可得7个连杆中任意两个相邻连杆之间坐标变换矩阵，由于坐标系{6}固定于末端执行器上，因此，机械手臂末端执行器相对于基坐标系{0}变换矩阵F为

(10)

通过式(10)转换矩阵进行变换，即可根据各关节的运动计算出末端执行器的运动轨迹，从而进行机器人运动学仿真。同时，在求解机器人正运动解的过程中，得到了相邻连杆的变换矩阵，为机器人逆运动学方程的求解奠定了基础。

机器人逆运动学方程的求解过程与正解过程相反。根据打磨轨迹计算出末端执行器的变换矩阵F，反推出另外6个关节的运动轨迹。目前逆解的求解主要有解析法、几何法和数值法3种求解方式。计算出机器人末端执行器的运动轨迹后，可通过式(10)依次各个关节的转角。

4 机器人运动轨迹计算有效性验证

在进行曲面抛光轨迹规划之前，首先通过规划机器人实现一个简单抛光路径的运动，从而对正运动学方程和逆运动学方程的求解算法进行有效性验证。使机器人末端执行器实现字符“ME”轨迹，如图5所示，其中，字母M高200 mm，宽200 mm，与字母E之间的距离为20 mm，E高200 mm，上、中、下的宽度分别为60 mm、40 mm和80 mm。

图5 字符串“ME”的打磨轨迹示意图

机器人的末端执行器从“start”点出发，一共经过26个拐点到达“end”点。根据上述逆运动方程组的求解方法，计算机器人各关节的转角，使得末端执行器根据图5所示的轨迹运动。设置插补时间为0.02 s，在水平和垂直方向的最大运动速度分别均为0.1 m/s。则通过追踪各关节的运动状态可以发现机器人关节运动幅度较小，处于相对安全的运动范围。而且关节的角速度均保持在1°/s以内，运动速度较低。只在接近加工终点处，各关节的速度和加速度变化均较为剧烈，这是因为机器人的运动轨迹从一条直线转过90°至另一条直线，速度方向变化巨大。最终加工段为一条相对较长的直线，角速度可在满足速度约束的范围一直增加，以保证加工效率，且尽量使得各关节运动速度在终点时为0。

图6 加工轨迹与目标轨迹的误差

通过对运动方程组逆向求解，得到了一组机器人关节运动的解，但机器人末端执行器的最终轨迹需要通过正运动方程计算得到。为进一步验证机器人的抛光运动轨迹与目标规划轨迹的相符程度，基于上述逆运动的解，通过正运动方程进行计算，得到机器人末端执行器的轨迹，与目标规划轨迹的绝对误差如图6所示。

从图6可以看出，通过逆向求解之后再正向求解，运动轨迹与规划轨迹存在一定计算误差，但对于10-1m级别的打磨路径，其数值计算误差较小，处于可接受范围内。因此，本文所述的机器人运动方程正、逆求解算法均有效。

5 结束语

介绍了机器人空间坐标的表示方法和变换算法，并根据所选6自由度机器人的结构参数和各关节的运动学关系，基于D-H方法建立了机器人运动学模型。同时，给出了正运动方程和逆运动方程求解过程，并通过字母轨迹“ME”对运动方程求解算法的有效性进行了验证。结果表明：机器人末端执行器的运动轨迹与目标轨迹的误差较小，满足抛光打磨的精度要求。机械手各关节速度变化率较小，且转角变量均位于设计范围内，说明了本文所用方法的有效性，为进行高难度的复杂曲面打磨奠定了的基础。本文仅实现了机器人运动轨迹规划，但关节的角速度变化规律和角加速度变化规律不太平滑，可以通过考虑B样条、人工智能的规划方法，优化机器人关节运动规律。

[1] Takeuchi Y, Ge D, Asakawa N. Automated polishing process with a human-like dexterous robot[C].Taipei:International Conference on Robotics and Automation,,IEEE,1993.

[2] Lee M C, Go S J, Jung J Y, et al. Development of a user-friendly polishing robot system[C].Nanjing:IEEE/RSJ International Conference on Intelligent Robots and Systems,1999.

[3] Ahn J H, Shen Y F, Kim H Y, et al.Development of a sensor information integrated expert system for optimizing die polishing[J].Robotics and Computer-Integrated Manufacturing,2001,17(4): 269-276.

[4] Lee M C,Go S J,Lee M H,et al.A robust trajectory tracking control of a polishing robot system based on CAM data[J].Robotics and Computer-Integrated Manufacturing,2001,17(1):177-183.

[5] Tsai M J,Fang J J,Chang J L.Robotic path planning for an automatic mold polishing system[J].International Journal of Robotics and Automation,2004,19(2):81-90.

[6] 袁楚明,张雷.机器人辅助模具自动抛光研究及发展趋势[J].中国机械工程,2000,11(12):1428-1430.

[7] 张雷,袁楚明,陈幼平,等.模具曲面机器人抛光工艺过程的建模与仿真[J].华中科技大学学报:自然科学版,2001,29(4):50-52.

[8] 袁楚明,张雷,陈幼平,等.模具曲面机器人智能抛光系统的研究[J].高技术通讯,2001,11(9):76-80.

[9] 杨林.复杂曲面机器人自动研磨抛光控制的研究[D].沈阳:东北大学,2011.

[10] 金鹏,刘建新,史素敏.抛光直角坐标机器人控制系统设计[J].机械设计与制造,2013(9):200-202.

[11] 周雪峰,李凯格,莫庆龙,等.多角度自动抛光系统及其抛光方法，中国:CN104290014A[P].2015-01-21.

[12] 周雪峰,李凯格,莫庆龙,等.自动抛光系统及其抛光方法,中国:CN104275638A[P].2015-01-14.

[13] 王平.模具自动抛光机器人的运动控制研究[D].长沙:湖南大学,2007.

[14] 向丹.基于自适应采样的复杂曲面抛磨轨迹生成算法及其性能对比[J].组合机床与自动化加工技术,2015 (6):17-19.

[15] 彭吉平.协作式抛光机器人系统运动学及轨迹规划研究[D].南昌:华东交通大学,2008.

[16] 冯海涛.机器人自动化抛光系统关键技术的研究[D].杭州:浙江大学,2015.

[17] Tam H,Lui O C,Mok A C K.Robotic polishing of free-form surfaces using scanning paths[J].Journal of Materials Processing Technology,1999,95(1):191-200.

[18] Chaves J J,Linares J M,Sprauel J M.Improving tool wear and surface covering in polishing via toolpath optimization[J].Journal of Materials Processing Technology,2013,213(10):1661-1668.

[19] 王伟,贠超,张令.机器人砂带磨削的曲面路径优化算法[J].机械工程学报,2011,47(7):8-15.

Polishing Robot Kinematics Model Based on the D-H Method

SONG Xiuyang，CHEN Jinjie，YU Jie

(School of Mechanical Engineering, University of Shanghai for Science and Technology, Shanghai 200093, China)

In order to improve the quality of free curved surface, we propose a robot motion model for planning the machining path of each joint. The idea of D-H notation is introduced to solve the robot inverse kinematics equation for the trajectory of the end of the actuator, thus achieving the robot’s kinematics simulation. The robot end executor performs a character "ME" trajectory to show the concrete application. The trajectory of the robot provides theoretical basis for more intelligent and efficient free-form surface polishing treatment automation.

D-H notation; kinematics model; direct and inverse kinematics equations; validation

2016- 07- 17

宋修洋(1991-)，男，硕士研究生。研究方向：智能机器人。陈劲杰(1969-)，男，副教授，硕士生导师。研究方向：智能机器人等。

10.16180/j.cnki.issn1007-7820.2017.06.014

TP24

A

1007-7820(2017)06-050-04