基于新维无偏灰色马尔可夫的农产品产量预测模型
陈宝平,于海英
(内蒙古财经大学 计算机信息管理学院,内蒙古 呼和浩特 010051)
基于新维无偏灰色马尔可夫的农产品产量预测模型
陈宝平,于海英
(内蒙古财经大学 计算机信息管理学院,内蒙古 呼和浩特 010051)
针对农产品产量随机性和波动性的特点,建立了新维无偏灰色马尔可夫的预测模型。该模型是在传统灰色马尔可夫理论的基础上,对马尔科夫模型进行了改进,提高了预测精度。通过无偏灰色模型预测变化趋势,借助马尔可夫模型处理随机性波动,同时在每一步的预测中,用新信息代替旧信息,对原始数据进行等维处理,更新建模数据。以人均粮食产量为例进行仿真实验,平均相对误差达到0.25%,且预测误差的变化波动性减小。结果表明,提出的模型有较好的预测精度,能够满足农产品产量预测精度的要求,适合中长期预测。
农产品产量;灰色理论;灰色马尔可夫模型;相对误差
农产品包括粮食、油料、蔬菜、肉蛋奶、水产品等种类,是居民生活必需品[1],是人类最基本的生存保障。我国是农业大国,农产品的产量高低直接关系到我国的民生大计。有效地进行农产品产量预测,能够为政府的宏观调控提供依据,对提高人民生活水平起着重要的作用。农产品产量随时间变化,同时又受到多个因素的影响,具有随机性和波动性的特点。传统农产品产量预测方法主要有指数平滑法、线性回归和时序分析等线性模型,适用于短期农产品产量预测。目前出现了支持向量机、神经网络、马尔可夫模型、粗糙集理论等非线性预测方法,包括一些组合预测的方法,提高了农产品的预测精度[2-7]。
灰色预测模型具有数据少、短期预测精度高的特点,马尔可夫模型适合于随机性和波动性较大的预测问题。将两者相结合,即灰色马尔科夫模型,可以优势互补,适合于农产品产量的预测。为进一步提高预测精度,本文在传统灰色马尔可夫理论的基础上,对马尔科夫模型进行了优化,提出了一种新维无偏灰色马尔可夫的农产品产量预测模型。首先用无偏灰色预测模型对原始数据进行拟合,得到数据的变化趋势;然后用改进的马尔可夫模型对拟合的数据分析预测,给出转移状态矩阵和新模拟序列;每一步的预测中,用新信息代替旧信息,对原始数据进行等维处理,更新建模数据。该模型不但具有短期预测精度高的优点,而且也适合中长期预测。
1 新维无偏的灰色马尔可夫模型
1.1 无偏灰色马尔可夫模型
无偏灰色马尔可夫模型是将无偏灰色GM(1,1)和马尔可夫相结合[8-10]。设原始序列X(0)={x(0)(1),x(0)(2),…,x(0)(n)},其中x(0)(k)≥0,k=1,2,…,n,用该数据序列构建模型,具体步骤如下:
步骤1 对原始数据序列作一阶累加,生成数据序列
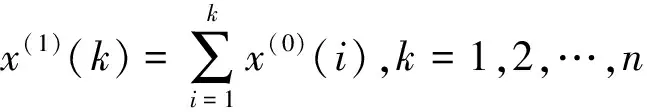
(1)
步骤2 确定数据矩阵B,Yn,其中
(2)
步骤3 用最小二乘法计算线性微分方程的待估参数[11],得到序列
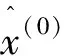
(3)

步骤5 计算由状态⊗i转到状态⊗j的m步状态转移概率P(m);
步骤6 判断需预测数据所处的状态⊗i,取该区间的中点作为预测值。
1.2 新维无偏的灰色马尔可夫模型
在无偏灰色马尔可夫理论的基础上,为了提高了预测精度,对马尔科夫模型进行了改进。 传统的灰色马尔可夫模型中,通过考察一步状态转移矩阵P(1),可确定预测对象的下一步转移状态。当矩阵P(1)中某行有2个或2个以上相同或相近时,可以参考二步P(2)或m步P(m)状态转移矩阵来确定状态的未来转向[12]。

(1)当k=1,…,n-1时,划分状态之后,状态是确定的,取该区间的中点作为拟合值

(4)
(2)k≥n时,状态未知。设k=n时,根据马尔可夫预测模型Q(n)=Q(0)P(1)=(q1,q2,…,qm)(其中Q(n)为n时刻的状态概率向量,Q(0)为n-1时刻的状态概率向量,P(1)为一步状态转移概率),计算状态的概率向量。未来的转移状态和转移概率qi确定之后,也就确定了预测值的变动区间⊗i=[⊗i1+⊗i2],则预测值为

(5)
若k=n+1时,预测模型Q(n+1)=Q(0)P(2),以此类推。
为了提高预测精度,引入新维无偏灰色马尔科夫模型:对原始序列X(0)做等维新息处理,即将最新预测的X(0)(n+1)值补充到已知数列后,同时去掉原始序列中的数据X(0)(1),保持数列等维;然后对新得到的序列再次进行无偏灰色马尔科夫预测,如此反复操作,直到完成预测目标。新维无偏灰色马尔科夫模型,不断补充新信息去掉“历史”信息,建模序列能够更好的反映系统目前的特征,进而提高中长期发展预测的准确度[13]。
2 预测农产品产量的实例
为验证农产品产量的新维无偏灰色马尔可夫预测模型的性能,以人均粮食的产量为例进行仿真实验。选取《中国统计年鉴》公布的2006~2015年人均粮食产量(kg) 数据,作为原始序列(见表1的“实际值”列)
X(0)={ 379.89,380.61, 399.13, 398.7, 408.66, 425.15, 436.5, 443.46, 444.95,453.2}
2.1 人均粮食产量的灰色GM(1,1)预测
根据式(1)~式(3),结合Matlab编程,可以得到相应时间响应函数

预测结果如表1“无偏灰色预测”列中的“预测值”。该模型的平均相对误差为1.10%,平均精度为98.9%。
2.2 人均粮食产量的马尔可夫预测


而2016~2018年状态未知,根据式(5)计算各自的概率向量。因2015年处于状态⊗3,初始时刻的Q(0)=(0,1/3,2/3,0),计算2016年的概率向量和预测值
Q(10)=Q(0)P(1)=(0.08,0.22,0.62,0.08)

同理可以计算出2017和2018年的预测值,分别为477.90和488.05。
2.3 人均粮食产量的新维无偏马尔可夫预测
使用改进的灰色马尔可夫模型预测人均粮食产量,精度接近一级,因此可以将2016年预测值467.16,作为最终的预测结果。对原始序列进行等维新息处理,去掉2006年的数据,加入2016年最终预测值。以2007~2016年人均粮食产量作为新的数据序列,建立灰色预测模型

(10)
然后用马尔可夫模型拟合2007~2016年的人均粮食产量(见表1中的“新维无偏灰色马尔可夫”列),平均相对误差值为0.23%,平均精度为99.75%。其中预测2017和2018年的人均粮食产量分别为476.24和486.63。 将2017年的预测结果 476.24作为最终结果。去掉2007年的原始数据,加入2017年最终的预测结果,再次构造数据序列,预测出2018年的人均粮食产量为491.35。

表1 2006~2018年人均粮食产量统计
注:表中数据来自2006~2015年《中国统计年鉴》人均粮食产量
2.4 结果分析
2.4.1 模型比较
根据前述实例中的3种模型:无偏灰色GM(1,1)、无偏灰色马尔科夫和新维无偏灰色马尔科夫模型,做出的预测结果做出对比。从表2可以看出,新维无偏灰色马尔可夫模型中,平均相对误差0.25%,预测精度达到一级,是一种有效的、拟合精度高的农产品的产量预测方法,尤其是在中长期预测中更具优势。
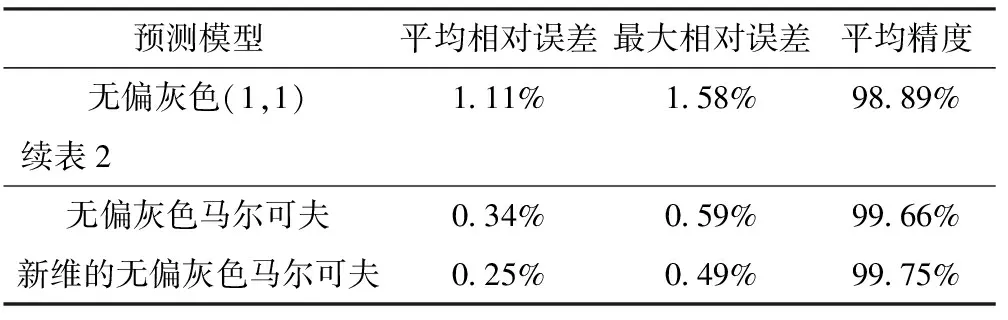
表2 3种预测模型的性能比较
2.4.2 新维无偏灰色马尔可夫模型优点
本文所提出的新维无偏灰色马尔可夫模型,是将无偏GM(1,1)与改进的马尔可夫相融合的模型,从预测的结果可以得到结论:
(1)单一的无偏灰色GM(1,1)模型的预测效果不理想,主要是因为单一模型只能反映产量变化的片断信息,无法全面、准确描述动态变化规律。而灰色马尔可夫模型既能揭示宏观规律,也能反映非线性波动规律,预测精度和可靠性有了较大提高,避免了单一模型的局限性;
(2)在任何一个灰色系统的发展过程中,随着时间的推移,将会不断地有一些随机扰动或驱动因素进入系统,使系统的发展相继受其影响。越向未来发展,即越是远离时间原点,模型的预测准确度越低。新维无偏灰色马尔可夫模型,预测过程中剔除了一些“老”信息,将进入系统的新信息置入到X(0)中,提高了预测精度,减少了人均粮食产量预测误差。
3 结束语
农产品生产是一个多因素影响的不确定系统,寻找有效的产量预测模型,对国家调整各种农产品政策、保障国内农产品安全都具有非常重要的指导意义[14-15]。本文以人均粮食为例,采用新维无偏灰色马尔可夫模型进行预测,实验表明,达到了一级预测精度。该模型可以推广于其它农产品产量预测。
[1] 李夏培.基于灰色线性组合模型的农产品物流需求预测[J].北京交通大学学报;社会科学版,2017,16(1):120-125.
[2] 肖培灵.基于灰色支持向量机组合模型的农产品产量预测[J].中国农机化,2010(1):44-49.
[3] 郑建安.主成分和BP 神经网络在粮食产量预测中的组合应用[J].计算机系统应用,2016(11):274-278.
[4] 张成才,陈少丹.BP 神经网络在河南省粮食产量预测中的应用[J].湖北农业科学,2014(8):1969-1971.
[5] 李蓬勃,闫晓冉,徐东瑞.BP 神经网络和多元线性回归在粮食产量空间分布预测中的比较[J].干旱区资源与环境,2014(9):74-79.
[6] 高丽媛,董甲.基于改进的BP神经网络洪峰预测模型[J].电子科技,2015(3):40-42.
[7] 向昌盛,张林峰.灰色理论和马尔可夫相融合的粮食产量预测模型[J].计算机科学,2013(2):245-248.
[8] 陈宝平.灰色关联系统的设计与实现[J].电子科技,2015(12):104-106.
[9] 王珊,许丽娜.基于灰色马尔科夫模型的中国女子中长跑的预测[J].数学的时间与认识,2016,46(24):59-63.
[10] 刘思峰,党耀国,方志耕,等.灰色理论及其应用[M].4版.北京:科学出版社,2015.
[11] 周庆元.基于灰色马尔可夫模型的粮食产量预测方法[J].统计与决策,2012(17):64-68.
[12] 赵玲,许宏科.基于新维无偏灰色马尔可夫的交通事故预测[J].计算机工程与应用,2013,49(7):35-38.
[13] 陈宝平.基于新维无偏灰色马尔科夫模型的围栏草场面积的预测[J].数学的实践与认识,2013,43(12):58-63.
[14] 谢继蕴.农产品省际流通成本的测度设计与分析[J].统计与决策,2017(4):120-125.
[15] 杨克磊.应用灰色GM(1,1) 模型的粮食产量预测研究[J].重庆理工大学学报:自然科学,2015(4):124-130.
The Frediction Model to Agriculture Products Yield Based on New Information Grey Markov
CHEN Baoping,YU Haiying
(School of Computer Information and Management,Inner Mongolia University of Finance and Economics,Hohhot 010070,China)
The agriculture products yield has the characteristics of random and fluctuation,so this paper proposed a prediction model to agriculture products yield based on grey theory . Based on the traditional grey forecasting model and Markov chain theory, equal dimension and new information unbiased grey Markov forecasting model was established.The development tendency is imitated by the unbiased Grey model, and the stochastic volatility is dealt with by the Markov model. The newest data are gradually added while the oldest one is removed from original data sequence. The simulation experiment was carried out with food production per capita as an example,and the average relative error is 0.25%. Case study showed that the model has fewer errors and better forecasting precision, especially for medium and long-term prediction.
agriculture products yield; gray theory; gray Markov model; relative error
2017- 03- 17
内蒙古自然科学基金(2015MS0607)。
陈宝平(1970-),女,教授。研究方向:最优化理论与算法。
10.16180/j.cnki.issn1007-7820.2017.06.009
TP391.72
A
1007-7820(2017)06-030-04

