傅里叶变换轮廓术的Matlab仿真实现

吴应山，张启灿

(四川大学 电子信息学院，四川 成都 610064)



傅里叶变换轮廓术的Matlab仿真实现

吴应山，张启灿

(四川大学 电子信息学院，四川 成都 610064)

在傅里叶变换轮廓术测量方法中，测量系统从一个角度投影结构光场，系统中的成像装置从另一个角度获取由物体高度调制后的变形光场，并通过傅里叶变换、频域滤波和傅里叶逆变换恢复出物体的高度信息。FTP测量方法中，关于傅里叶变换，相位展开的相关知识，涉及大量复杂的数学运算使其抽象难以理解。针对这一问题，文中设计了基于Matlab的仿真实验。根据相应原理编写了仿真代码，运用Matlab的数学运算和可视化功能，模拟整个测量流程，完成了仿真实验。这有助于学习和理解FTP测量方法原理及相关知识。

傅里叶变换轮廓术；Matlab；相位展开

随着计算机技术的发展，三维数字化技术逐步成熟，并广泛用于各个领域[1-3]，傅里叶变换轮廓术是1983年由M.Takeda和K.Mutoh将傅里叶变换用于三维物体的测量中而提出的三维面形测量技术[4]，只需采集一或两幅变形条纹图，就可以进行三维重构，实现对物体轮廓的测量。所以测量速度快、易于实现，适合测量动态物体的三维面形[5-7]。在实际应用中，可使用MFC与Opengl开发三维测量软件[8]进行测量。Matlab是Mathworks公司推出的一款数学软件，它集数值分析、矩阵计算、信号处理和图形显示于一身，是一种简洁、高效的编程工具[9]。运用Matlab Gui设计数据分析界面[10]，可提高数据分析的效率。

1 傅里叶变换轮廓术

FTP(Fourier Transform Profilometry)测量光路如图 1所示，投影仪和CCD的光轴相交于O点，O为参考平面的原点，建立如图1所示的坐标轴。A和B分别是投影仪的出瞳和CCD的入瞳，d为A与B间的距离，L是B到参考平面R的距离，h为物面上H点到R的距离，光心连线AB与参考平面R平行，在FTP中，当投影正弦光栅产生的结构光场经过物体表面的反射，由成像系统得到的变形条纹可表示为

I(x,y)=a(x,y)+b(x,y)cos(2πf0x+φ(x,y))

(1)

其中，a(x,y)是背景光强；b(x,y)是条纹对比度；f0是投影光栅的频率；j(x,y)是由物体高度分布h(x,y)引起的相位调制。为得到相对高度分布和消除系统测量误差，对参考平面进行测量，对于物体高度h(x,y)=0的参考变形条纹可表示为

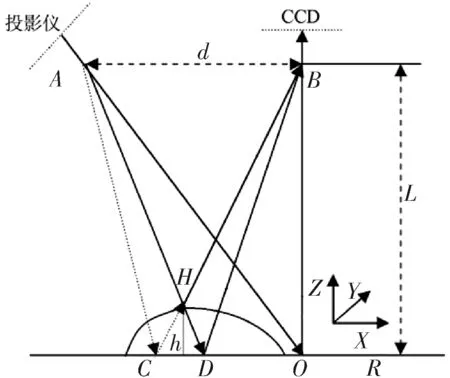
图1 FTP光路图

I0(x,y)=α(x,y)+b(x,y)cos(2πf0x+φ0(x,y))

(2)

在图1中，AC投影到参考平面的位置为C，经光线CB在CCD阵列上成像，光强为I0，调制相位为φ0(x,y)，当投影在被测物体上时，对同一条光线AC而言，由于光线CB和物面产生交点H，通过CCD观察到的H点的光强为I，相当于参考面上D点在CCD中的光强，由物体高度h(x,y)产生的调制相位为φ(x,y)，则二者的相位差为[1]

(3)

由ΔAHB与ΔDHC的相似关系与式(3)得到

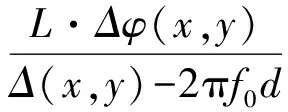
(4)

为便于进行傅里叶变换，将式(1)和式(2)改写为指数形式

I(x,y)=a(x,y)+q(x,y)ej2πf0x+q*(x,y)e-2πf0x

(5)

I0(x,y)=a(x,y)+q0(x,y)ej2πf0x+q0*(x,y)e-2πf0x

(6)

上式中,*表示取共轭。对式(5)进行二维傅里叶变换可得

F(u,v)=A(u,v)+Q(u-f0,v)+Q*(u+f0,v)

(7)

其中，A(u,v)对是a(x,y)的二维傅里叶变换，Q(u-f0,v)，Q*(u+f0,v)分别是q(x,y)和q*(x,y)的二维傅里叶变换，其频谱示意图如图2所示。

图2 傅里叶频谱分布示意图

图2中虚线包围的频谱为包含物体高度变化的有用信息，选用适当的带通滤波窗口将基频分量Q(u-f0,v)滤出，再计算其傅里叶逆变换。即

(8)

其中，F-1表示二维傅里叶逆变换，同样对参考条纹也进行二维傅里叶变换并滤波，傅里叶逆变换处理后可得

(9)

通过式(8)与式(9)得到s(x,y)与s0(x,y)进行下列运算，获取相位差

(10)

式中，atan{·}表示反正切函数；imag[·]表示取复数虚部；real[·][11]表示取复数实部，得到的相位差通过相位展开技术，获取连续相位，根据式(4)恢复出物体的高度信息h(x,y)。

2 相位展开方法

假定满足抽样定理的要求，即抽样频率大于最高空间频率的2倍。则任何两个相邻抽样点之间的连续相位差变化在(-π,π)内，用Matlab中的atan2函数将式(10)改写为

(11)

经转换后得到的二维相位呈现不连续的截断分布，须用相位展开技术，消除相位分布中的截断跳变展开成连续的相位，才能恢复高度信息。

1982年Itoh分析了一维相位展开问题，建立了严谨的数学模型，并且得到包裹相位图的相位差分的再包裹就是实际相位图的相位差分，相位展开实际上是对包裹相位差分再包裹值的积分过程[12-14]，此思想就是路径跟踪算法的基础。在无噪声或者其他干扰的理想情况下，只需沿着相位图的行和列，逐点将相位展开即可。对于二维相位图x方向展开后的相位值用up表示[15]

up(xk,y)=wp(xk,y)-2nkπ，nk∈Z

(12)

其中，wp(xk,y)是展开前的截断相位；(xk,y)为采样点的像素坐标，根据任何两个相邻抽样点之间的连续相位变化<π，即

-π

(13)

根据式(12)与式(13)，得到式(14)

-π<[wp(xk,y)-wp(xk-1,y)]-2nkπ+2nk-1π<π

(14)

将式(14)加π,再除以2π得到

0<[wp(xk,y)-wp(xk-1,y)]/2π+0.5-nk+nk-1<1

(15)

对不等式各项同时向下取整得

nk=floor{[wp(xk,y)-wp(xk-1,y)]/2π+0.5}+nk-1

(16)

floor是Matlab中的向下取整函数，根据此分析，假定第一点截断相位为已知的相位，则n0=0，编写uphase1d函数，输入不连续的截断相位wp，输出连续相位up。

function up = uphase1d(wp)

n= zeros(size(wp));

for i=2:length(wp)

n(i) = floor((wp(i)-wp(i-1))/(2*pi)+0.5)+n(i-1);

end

up = -2*pi*n + wp;

end

同理，上述方法对也对y方向的相位展开适用。假定二维截断相位图(1,1)点的相位为已知相位，由此点完成第一行的相位展开，然后再以展开的第一行各点为基准点，逐列展开，最后得到连续分布的二维相位。

function up = uphase2d(wp)

[r,c]= size(wp);

wp(1,:) = uphase1d(wp(1,:));%第一行的相位展开

for n = 1:c

wp(:,n) =uphase1d(wp(:,n));%各列的相位展开

end

up = wp;

end

3 计算机仿真实验

3.1 FTP仿真实验流程图

根据傅里叶变换轮廓术的基本原理，设计仿真实验流程图如图3所示。

3.2 在Matlab中仿真FTP测量方法

根据图1所示，设置系统参数L=800 mm，d=350 mm，模拟的被测物体大小为512 pixel × 512 pixel的peaks函数，如图4所示。

图4 模拟物体

投影周期为p=8 pixel正弦参考条纹，当参考条纹投影到被测物体时，由于物体高度的变化，使参考条纹的相位发生变化将发生形变。分别对参考条纹与变形条纹做二维傅里叶变换，将得到它们的频谱，用鼠标选取滤波范围，将自动生成矩形滤波窗。根据式(10)获取截断相位差，如图5所示。

图5 截断相位

图6 展开后的连续相位

调用uphase2d函数将二维截断相位展开成二维连续相位，如图6所示。根据式(4)进行恢复物体高度信息，还原后的物体如图7所示。

图7 恢复后的物体

图8 误差分布图

用恢复后的物体减去模拟的物体，得到其误差的分布图如图8所示。其误差分布较大，是由于用矩形滤波窗进行频谱滤波时，会产生频谱泄漏造成的。恢复后最大误差为2.73 mm，平均误差为0.154 mm。

FTP仿真实验的Matalb代码如下

N = 512;L = 800;d = 350;p = 8; f0=1/p; a = 127.5; b = 127.5;

x = 0:1:N-1;[X,Y] = meshgrid(x);object =5.6*peaks(length(x));

I0 = a+b*cos(2*pi*f0*X);I = a+b*cos(2*pi*f0*(X +(d/L*object)));%产生变形条纹

F0 = fftshift(fft2(I0)); F = fftshift(fft2(I)); %二维傅里叶变换

rect_window_filter= zeros(size(F));

figure,contour(abs(F),80);r = round(getrect);%用鼠标选取滤波范围

rect_window_filter(r(2):r(4)+r(2),r(1):r(3)+r(1)) = 1; %生成矩形滤波窗

Q = rect_window_filter.*F; Q0 = F0.*rect_window_filter;%滤波

s0 = ifft2(ifftshift(Q0)); s = ifft2(ifftshift(Q));%逆傅里叶变换

Deltaphi= atan2(imag(s.*conj(s0)),real(s.*conj(s0))); %获取相位差

up = uphase2d(Deltaphi); %截断相位展开成连续相位

recovery_object = L*up./(2*pi*f0*d-up); %恢复物体高度

4 结束语

本文对FTP的基本原理进行了介绍、并对理想条件下相位展开方法进行了推导，文中的仿真实验采用的是远心光路，平行光投影方式，用鼠标选取滤波范围生成矩形滤波窗进行滤波。在相位展开方法上，假定无噪声无干扰、满足抽样定理的理想条件下，根据相邻像素相位差为依据进行相位展开。在Matlab中恢复了模拟物体的三维形貌，完成了整个仿真实验。

[1] 苏显渝,李继陶.信息光学[M].北京:科学出版社,2013.

[2] 苏显渝,张冠申,陈泽先,等.鞋楦三维面形光电自动测量系统[J].光学工程,1989(6):1-5.

[3] 金国藩,李景镇.激光测量学[M].北京:科学出版社,1998.

[4] Takeda M,Mutoh K.Fourier transform profilometry for the automatic measurement of 3-D object shapes[J]. Applied Optics,1983,22(24):3977-3982.

[5] 张启灿,苏显渝.动态三维面形测量的研究进展[J].激光与光电子学进展,2013,50(1):1-14.

[6] 张启灿.动态过程三维面形测量技术研究[D].成都:四川大学,2005.

[7] 李剑,苏显渝,陈峰,等.基于傅里叶变换轮廓术的动态爆轰过程研究[J].激光杂志,2005,26(2):47-48.

[8] 廖宏刚,刘荣.基于OpenGL的三维真实感地形的实现[J].电子科技,2013,26(9):164-165.

[9] 胡新艳,霍文晓,李爱涛.Matlab在《信号与系统》课程教学中的应用[J].科技信息,2009(27):136-137.

[10] 李娅丽,忻尚芝,郑春雷.基于Matlab/GUI的数据分析界面设计[J].电子科技,2016,29(4):88-91.

[11] 刘卫国.Matlab程序设计与应用[M].北京:高等教育出版社,2006.

[12] Itoh K.Analysis of the phase unwrapping algorithm[J].Applied Optics,1982,21(14):2470-2470.

[13] 吴明云.二维相位展开算法的研究[D].天津:天津大学,2012.

[14] 肖枫. InSAR相位解缠算法的研究[D].上海:同济大学,2008.

[15] Macy W W. Two-dimensional fringe-pattern analysis[J].Applied Optics,1983,22(23):3898-3901.

Fourier Transform Profilometry Simulation in Matlab

WU Yingshan,ZHANG Qican

(School of Electronic Information, Sichuan University, Chengdu 610064, China)

In the method of Fourier transform profilometry (FTP), the measurement system obtains the deformation of the object height modulated light field by the imaging device, and restores the height information of the object through the Fourier transform, frequency domain filtering and Fourier inverse transformation. The Fourier transform and phase unwrapping knowledge in the FTP measurement method involves a large number of complex mathematical calculations, making it abstract and difficult to understand. In view of this situation, we design simulation experiments based on Matlab and prepare the corresponding simulation codes. The entire measurement process is simulated by using Matlab numerical calculation and visualization function, which helps to understand the principles of the FTP measurement.

Fourier transform profilometry; Matlab; phase unwrapping

2016- 08- 31

国家重大仪器专项基金(2013YQ490879)

吴应山(1985-)，男，硕士。研究方向：动态三维测量。张启灿(1974-)，男，博士，教授，博士生导师。研究方向：三维传感等。

10.16180/j.cnki.issn1007-7820.2017.06.003

TN29

A

1007-7820(2017)06-009-04