“变换思想”在初中数学几何教学中的应用研究

☉江苏如东县袁庄镇袁庄初级中学 戴昌龙

“变换思想”在初中数学几何教学中的应用研究

☉江苏如东县袁庄镇袁庄初级中学 戴昌龙

变换思想在我国历史长河中源远流长，很多传统文化中都包含着变换的思想.随着社会的发展，这种变换的思想也被当成了一种研究工具应用到了更多的领域当中，例如，在物理学中的P-V图和V-T图、P-T图的变换，在化学中的傅里叶变化成像光谱技术的应用，在生物医学中的连续小波在医学信号处理中的应用，在数学学科中代数部分的正交变换和相似变换等.在新课程改革的实施过程中，就对初中生对几何变换思想的掌握提出了明确的要求：要求学生能够灵活掌握图形轴对称、图形平移、图形旋转、图形相似等几何图形的变换.

一、变换思想概述

变换思想就是利用相似的事物代替原有事物，通过这种迂回变换的方式达到解决问题的目的.通过对原有问题的转换，能够使原有未得到解决的问题向能够解决的问题转变，例如，数学教学中的分割变换法.在目前的初中数学教学中，数学变换思想得到了很多人的重视，在教学中我们不仅要将变换思想作为一种具体的解题思路来教育学生，还要将它当作一种数学思想来帮助学生开拓自己的思维.

二、变换思想在初中数学几何教学中的应用

1.变换思想能够辅助学生的解题.

变换思想不仅是一种重要的数学思想，还是一个有效的解题工具，利用变换思想能够帮助学生在解决几何问题时，发挥出奇制胜的作用.

例1 在四边形ABCD中，AB平行于CD，其中E是边AD的中点，连接BE和CE，其中BE和CE分别是∠ABC和∠BCD的角平分线，求证BC=AB+CD.

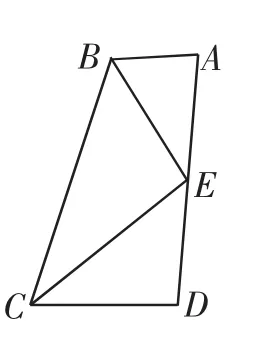
图1

图2

图3

这一问题涉及的AB和CD两条边的关系并不在学生熟悉范围之内，想要求证BC、AB和CD三条边的关系就需要将它们尽量安排在相同的图形当中.利用变换思想中的轴对称变换思想，通过添加辅助线能够实现快速解题.

证明：在四边形ABCD的边BC上找一点F，使BF=AB，连接EF，通过边角边定理，就可以得出三角形EBA和三角形EBF是全等三角形，该图形就构成了以BE为对称轴的两个对称图形，由此就可以得出∠A=∠BFE.又因为∠A+∠D=180°，∠BFE+∠CFE= 180°，所以∠CFE=∠D.根据角角边定理，就可以得出三角形FCE和三角形DCE是全等三角形，进而得出CF=CD.这样就可以将AB和CD转化到同一条线段当中：BC=BF+CF= AB+CD.

对于这一问题，我们还可以通过旋转变换的思想来完成证明.由于E点是线段AD的中点，AB∥CD，那么围绕点E旋转180°就可以得到另一个图形，就可以将线段AB和线段CD转化到同一个图形当中，从而帮助学生完成证明.

证明：延长BE和CD，相交于点G，通过角边角定理，我们可以得出三角形AEB和三角形DEG是全等三角形，那么AB=DG.因为BE是∠CBA的角平分线，那么∠ABG=∠CBG.又因为∠ABG=∠G，那么∠CBG=∠G.利用角角边定理就可以得出三角形CBE和三角形CEG全等，进而得出BC=CG.所以BC=CG=DG+CD=AB+CD.

为帮助学生进一步掌握该部分知识，教师还可以通过变换思想，利用变式将原有问题进行变换，从而加深学生对该类问题的理解.例如，在四边形ABCD中，AB平行于CD，其中E是边AD的中点，连接BE和CE，其中BE是∠ABC的角平分线，并且满足BC=AB+CD，求证：BC= AB+CD.

数学问题千变万化，利用变换思想能够帮助学生掌握一类问题的解决方法，能够引导学生从多个方面思考问题，从而帮助学生快速完成解题.

2.变换思想能够促进学生思维的发展.

在几何教学中，变换思想的关键就在于使变换前后的图形保持不变，利用轴对称变换、平移变换和旋转变换等方法，构造新的数量关系，从而完成问题的求解.这种方法能够帮助学生从其他角度去思考问题，开阔他们的思维，促进学生的思维发展.

例2 在等腰直角三角形ABC中，∠BAC=90°，AB= AC，其中P是等腰直角三角形内任意一点，BP=3，AP=2，CP=1，求∠APC的度数.

图4

图5

学生拿到这题目后的第一感觉就是：这个题目的已知条件与所求的问题之间并没有直接的联系，难以找到解题的突破口，他们不得不转化思维，向更深处思考.是否可以另外构造图形，将已知条件都用上？因为在题目给出的已知条件中说明了AC=AB，BP=3，AP=2，CP=1，我们就可以试图通过构造全等图形的方式，将要求的问题转化到相似的图形中.通常情况下，对于具有等边特性的图形来说，我们可以使用旋转的思想来辅助问题的解决.在含有直角的三角形中，我们经常以直角三角形的顶点为圆心进行旋转，将题目中包含的已知条件尽可能汇总到一个图形中，进而求出最终答案.

详细解题过程如下：以等腰直角三角形的顶点A为圆心，旋转90°，使得边AC与边AB重合，即可以得到与三角形APC全等的三角形AMB.由此可以看出∠MAP=90°，AP=.又因为BM=PC=1，BP=3，根据勾股定理的逆定理就可以得出三角形BMP是直角三角形，∠BMP=90°.因为在直角三角形MAP中，∠AMP=45°，所以∠BMA=∠BMP+AMP=135°.又因为三角形AMB是三角形APC旋转90°得来的，那么∠APC=∠AMB=135°.

这个问题对学生思维的要求较高，学生刚一接触难免会出现不知所措的情况，依靠传统的思维方式很难找到突破口，通过旋转变换的思想，巧妙地解决了看似无从下手的问题，开拓了学生的思维.通过变换思想改变了学生传统模式下机械做题的习惯，使他们的发散思维得到了发展，使他们养成了从多角度思考问题的习惯.

3.变换思想能够体现出数学中的美学.

学生是具有情感的高等动物，他们具有丰富的情感，通过体会数学中的美学，能够帮助学生建立数学学习的兴趣，感受数学的魅力.数学中的变换思想体现出了数学中的美学，同样的问题，通过不同形式的变换，能够展现出不同的结果，从而体现出数学的魅力.

1.涂荣豹.谈提高对数学教学的认识［J］.中学数学教学参考，2006（1/2）.

2.郑毓信，梁贯成.认知科学建构主义与数学教育——数学学习心理学的现代研究（第二版）［M］.上海：上海教育出版社，2002.

3.胡庆玲.“几何图形变换”教学设计［J］.数学教学研究，2005（11）.