基于改进K-means聚类算法在电力客户价值分群的应用

朱州吴漾

（贵州电网有限责任公司信息中心贵阳550003）

基于改进K-means聚类算法在电力客户价值分群的应用

朱州吴漾

（贵州电网有限责任公司信息中心贵阳550003）

针对电力客户特点实行不同的营销策略和提供差异化服务，就需要对电力客户做出准确的分群。传统K-means聚类算法对数据分布均匀的类似球形的数据集聚类效果比较好，一旦数据集分布密度不均衡，类簇大小差异明显时，传统K-means算法容易使稀疏的大类簇被高密度小类簇瓜分，导致电力客户分群正确率下降。论文基于电力客户数据分布不均衡的特点，采用了一种改进的K-means聚类算法。改进的K-means算法提出一个新的加权聚类准则，并根据该准则修改了聚类迭代过程。文章最后在对电力客户数据的分群聚类结果表明，改进的K-means聚类算法的分群聚类效果中各个群类的紧凑性得到有效提高，误分情况明显改善。

K-means算法；新聚类准则；迭代权重；正确率；标准差

Class NumberTP391

1 引言

21世纪是一个信息的时代，信息对于各行各业的影响都起到了一个至关重要的作用。面对目前供电企业每天都在产生和更新的庞大的企业运营管理数据，那么要怎样去利用这些数据，从众多凌乱的数据中挖掘出潜在的客户价值，进而帮助电力企业改进营销决策、降低运营成本、提高企业收益，是每个供电企业都在努力地方向［1］。数据挖掘技术作为一种可以在大量数据中发现潜在的信息的数据处理手段便在此脱颖而出，该技术已经成为处理电力行业信息化的建设过程中所积累的海量历史数据的重要手段，数据挖掘技术的应用也将会为供电企业提供一个更为广阔的发展空间［2］。

K-means聚类算法作为客户分类常用的一种数据挖掘技术手段，其本身存在着各方面的局限。首先，初始聚类中心选择的好坏在很大程度上会影响到聚类结果的好坏；其次，聚类的类别数没办法直接确定；同时，传统K-means算法不适合密度不均衡的数据集等等。针对传统K-means聚类算法的不足之处，已经有很多学者提出了改进的研究方案。李荟娆［3］提出了适用于非负、类椭球形数据的基于I-divergence测度的K-means聚类算法；张永晶［4］，翟东海［5］分别在确定初始聚类中心上提出了最大最小距离法和最大距离法以提高模型的聚类效果等等。

对于本文电力客户数据分布密度不均衡的特点，如果直接采用传统K-means聚类算法，显然会造成高密度小群瓜分低密度大群的现象，于是一个符合电力客户分布特点的改进K-means算法就显得尤其重要。本文采用的基于改进聚类准则，同时改进聚类迭代过程的K-means聚类算法［6］，应用在电力客户价值分群上的分群聚类结果表明，该改进的聚类算法是适合实际运营数据的，并且达到了提高聚类紧凑性的效果。更加优质的分群聚类结果也可以保证决策高效实施，最终为供电企业带来更高的收益。

本文应用的数据集来自贵阳供电局，考虑到客户价值的关键指标为用电量和电费，不同客户类在这两个指标上的数量级差异很大，直接进行处理会造成较大的偏差，故先对该数据集人工分成了重要客户、大客户、重点关注客户、居民客户、其他客户五个类数据，分别对这五个类数据的建模数据指标变量做了数据直方图分布情况分析后，可以认为该数据集存在密度差异明显，分布不均匀的特点。以居民客户类别为例，其建模指标分布直方图情况如图1所示。

对应数据直方图的各个参数取值情况如表1所示，其中，分位数可表示用于画直方图的数据占整个数据的百分比，范围最小值和最大值表示画直方图的整个数据区间左右端点值，区间大小表示直方图每个小区间内距离。

上面的数据分布直方图可以看出，不管从哪个指标变量的角度看数据分布，都呈现出密度明显不均，数据分布广的特点。因此，直接采用传统K-means聚类算法很容易造成瓜分稀疏大族类现象。进而本文针对贵阳供电局提供的数据特点，采用了基于改进聚类准则的K-means聚类算法，该算法可以有效地修正对于密度差异大，分布不均匀的数据集的聚类时误分情况，使得聚类精度可以得到明显的改善。

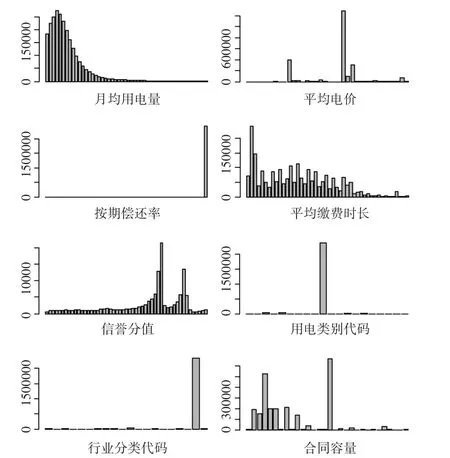
图1 各指标变量频数直方图

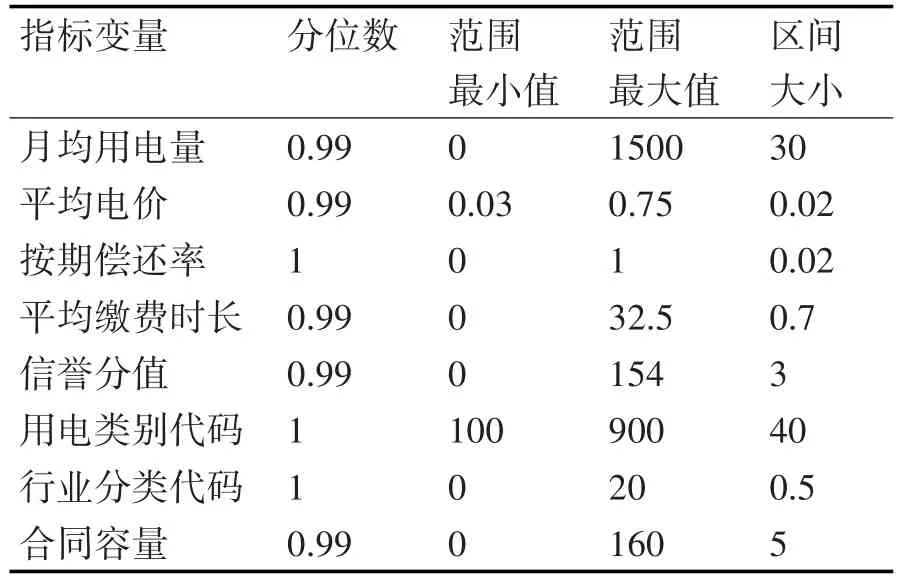
表1 直方图对应参数值

2 K-means算法及其改进

2.1 传统K-means聚类算法

K-Means算法是在最小化误差函数的基础上将数据划分为预定的类数K，采用距离作为相似性的评价指标，即认为两个对象的距离越近，其相似度就越大。

1）传统的聚类准则函数

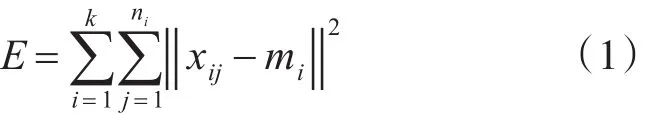
其中，ni代表第i个类的样本个数；xij代表第i个类中的第j个样本；mi代表第i个类的聚类中心。

2）算法过程

（1）从数据集（N）中随机选取K个对象作为初始聚类中心；

（2）分别计算每个样本到各个聚类中心的距离，将对象分配到距离最近的聚类中；

（3）所有对象分配完成后，重新计算K个聚类的中心：

（4）与前一次计算得到的K个聚类中心比较，如果聚类中心发生变化，转（2），否则转（5）；

（5）当质心不发生变化时停止并输出聚类结果。

传统K-means算法一般以欧式距离的大小度量数据对象的相似性，再加上其聚类准则函数以各个类内误差平方之和最小为最优质结果，使得传统算法更加适用于分布均匀，类似球形或超球体的数据。当数据分布不均衡时，该聚类结果的准确性也就会下降。

2.2 K-means聚类算法改进

2.2.1 聚类准则函数的改进

根据电力客户数据分布密度差异明显的特点，传统K-means算法对数据分布的要求使其显然已经不能满足供电企业对其数据进行挖掘探索的要求。本文采用的基于改进聚类准则的K-means算法，将数据集中各个类的标准差和类中数据对象的个数作为改进的聚类准则函数的参考因素，以降低高密度小类瓜分稀疏大类的风险。改进的聚类准则函数如式（3）所示：

其中，N代表数据集样本总个数，ni代表第i个类样本个数，σi代表第i个类的标准差［7］。

改进的聚类准则函数ε中的类内标准差σi可以使得类内数据对象尽可能靠近聚类中心，其作用与传统的聚类准则函数中各个类的误差平方值的总和起到的作用是类似的；权重的作用主要是增加数据对象比较多的样本类的标准差的贡献度。

与该改进的聚类准则函数相对应的，在聚类算法的迭代过程也做了相应的修改，即将数据重新归类到新的聚类中心时使用加权距离Wk·dist(Ck·x)取最小值的原则，权重为，该做法同样是以增加权重的形式达到数据集大小密度不均时样本也能准确归类的目的。

2.2.2 改进的K-means聚类算法

K-means聚类算法改进后，聚类迭代过程中样本对象不再被分配到距离最近的聚类中心的那个类，而是被分配到使加权距离Wk·dist(Ck·x)取最小值的那个聚类中心所在类。改进后的K-means聚类算法具体过程如下所示：

输入：数据集（包含N个样本）和预期类的个数（K）

输出：聚类效果最好的K个聚类结果

1）使用随机抽样的方法确定初始K个聚类中心，将N个样本对象分别分配到距离最近的聚类中心的那个类，获得最初的N个类。

2）用传统计算均值的方法计算出新的K个聚类的中心。

3）分别计算每个样本到各个新的聚类中心的加权距离Wk·dist(Ck·x)，将样本对象分配到加权距离最小的类别中。

4）所有样本对象重新分配完成后，再次计算K个聚类的中心，与前一次计算得到的K个聚类中心比较，如果聚类中心发生变化，转3），否则转5）。

5）当聚类中心不发生变化时停止并输出聚类结果。

3 实验验证

3.1 实验环境及模拟实验的数据

本模拟实验的数据集主要采用随机［8～9］生成的方式形成，具体步骤有：1）选取两个或三个相邻且大小不一样的矩形区间；2）在区间内随机生成若干个点数据。实验数据对象的x属性值可以用式（4）产生，y属性值可以用式（5）产生：

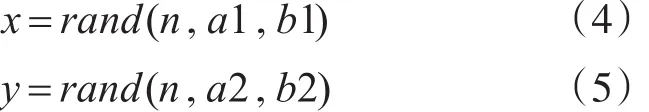
其中，rand表示在区间［a，b］上生成均匀分布的随机数，而n表示产生随机数的个数，a1，b1；a2，b2分别表示生成x，y的区间值。

实验使用的参数值如表2所示，对应的可视化图形如图2所示。

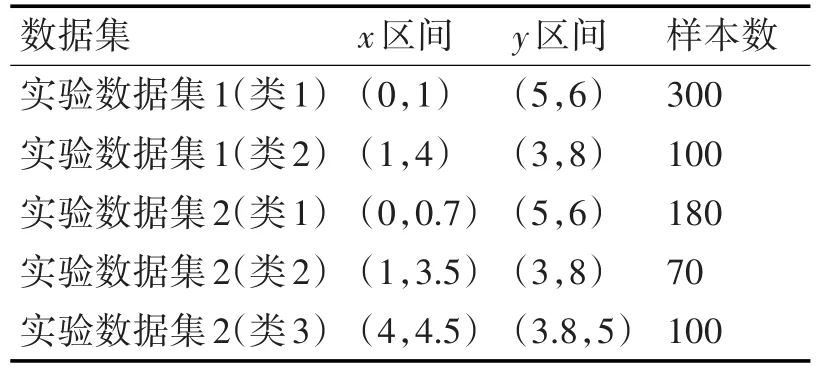
表2 实验数据集

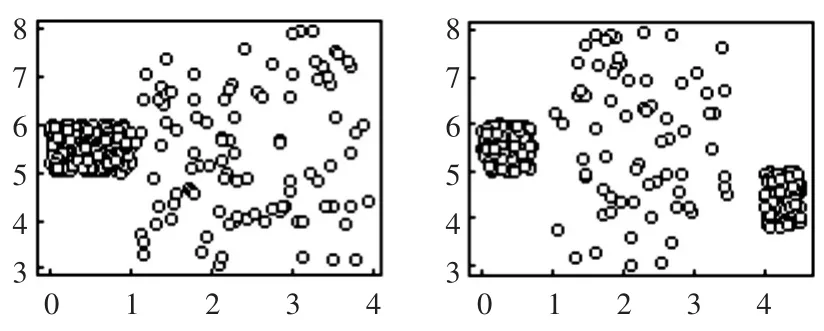
图2 实验数据集

3.2 实验的结果及其分析

根据生成的实验数据集1和实验数据集2，分别进行传统K-means算法聚类和改进K-means算法聚类，实验时前后两个算法使用的初始聚类中心是保持一致的。使用实验数据集1运行传统K-means算法和改进K-means算法的聚类结果如图3所示；实验数据集2运行两个算法的聚类结果如图4所示。

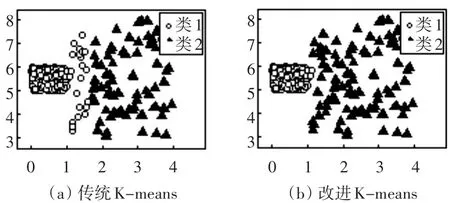
图3 实验1

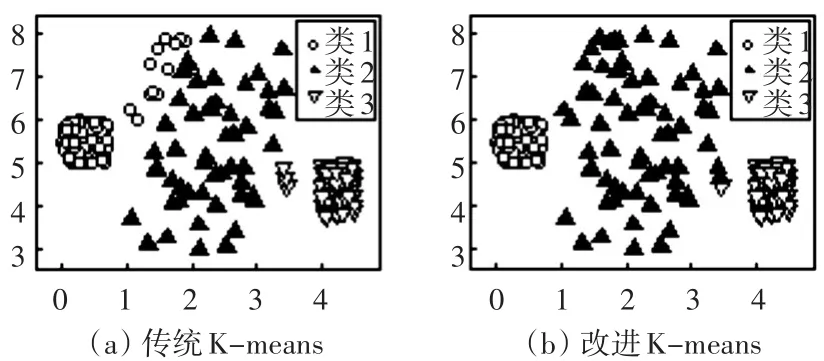
图4 实验2

对实验结果的标准差进行对比分析如表3所示。

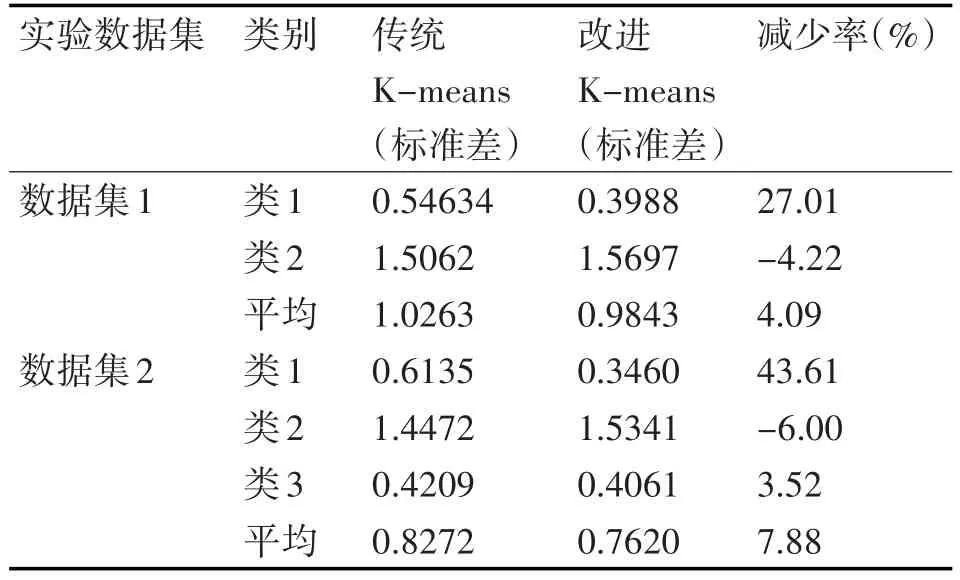
表3 实验聚类各类标准差对比

K-means聚类算法［10～11］其目的是要让类内数据对象相似度比较高，而类间的数据对象相似度较低的聚类结果，也就是得到的划分结果中每一个类都尽可能地紧凑或者集中。从表3可以看出，实验数据集1和实验数据集2的平均标准差分别减少了4.09%和7.88%，数据集1类2的标准差虽然增加了4.22%，其类1的标准差却减少了27.01%；数据集2中类2的标准差同样增加了6.00%，但是类1和类3却分别减少了43.61%和3.52%，总体来看，两个数据集中大而稀疏的类其标准差都轻微变差，但是却换来了其他小而密集的类标准差的显著改善，达到了提高整体类内数据紧凑性的效果［12］。

由此可见，改进K-means算法通过牺牲两个实验数据集中的原本松散的两个类，以提高整体的聚类效果。而原本松散的类本身就是缺少一些基本特性的类，其本身有可能是较为稀疏的类，亦或者是噪声点、异常值之类的数据，所以将较为密集的类周边的稀疏的数据划分给周边较松散的类，以达到整体聚类结果得到改进的效果。

4 改进K-means聚类算法在贵阳电力客户价值分群的应用

4.1 改进聚类准则确定K值

对电力客户数据进行数据探索性分析、预处理、变量标准化之后，需要先确定各类客户的最优聚类数K，改进的K-means聚类算法有其对应的新的聚类准则函数，考虑到聚类数目的实用性以及方便决策［13～14］，这里试行K值取2～5，并且取聚类准则值变化率最大的K值作为最优聚类数。分别对五大类客户数据进行极差标准化后，运行改进的K-means聚类算法可以得到表4所示的不同情况下的聚类准则值。

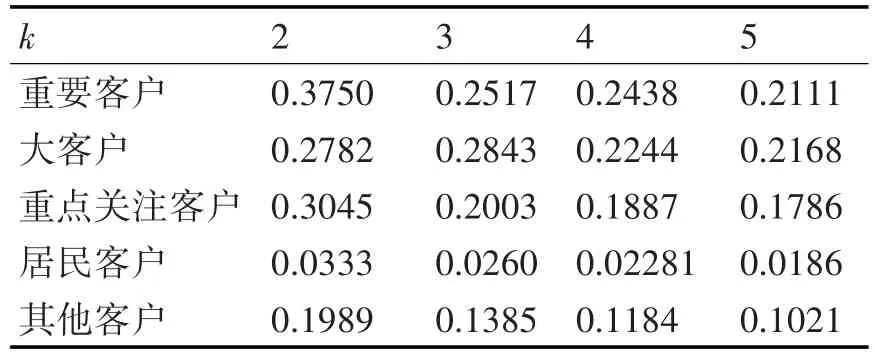
表4 各个情形下聚类准则值

将以上新的聚类准则值画成连线图，得到图5。

将五大类客户数据的聚类准则函数值进行如上所示的可视化展示，不难发现适合这五大类客户数据的最优聚类数，重要客户数据得到聚类准则函数值在K=3时变化率达到最大，K=4时准则函数值几乎没什么变化，故重要客户的最适合的分群数取3。大客户在K=3时的聚类准则值反而比K=2时的值还要大，当K取4时聚类准则值迅速收敛，即使K值继续增大准则值也只是小幅度的减少，故可以认为大客户的最优聚类数K取4最适宜。同样的方式确认重点关注客户、居民客户、其他客户的最适合K值，分别得到3，3，3；也就是所有客户类别最适宜K值取值情况如表5所示。

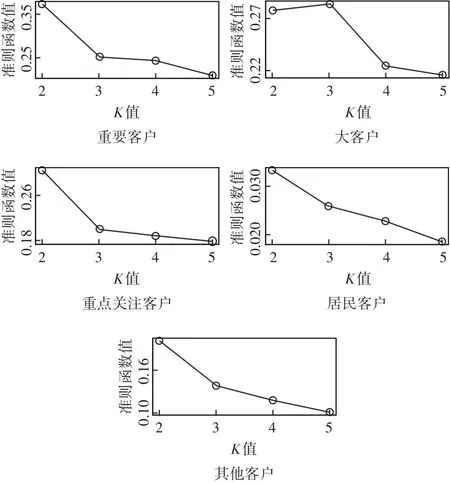
图5 五大类客户新聚类准则值

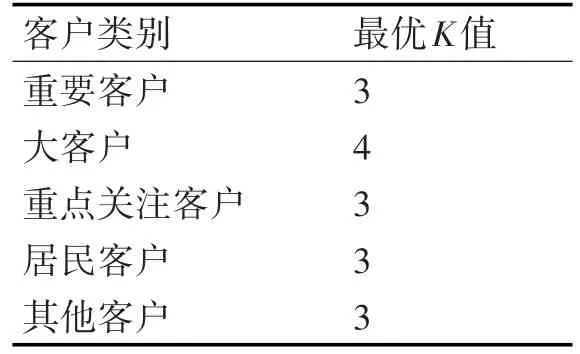
表5 各个客户类数据的最优K值

4.2 分群聚类结果比较分析

以上述分析各个类别客户K值的取值情况为标准对数据集逐一进行聚类［15］，为了对比K-means聚类算法改进前与改进后在贵阳电力客户分群聚类上的效果，本研究同步进行了传统K-means聚类算法和改进K-means聚类算法，对分别聚类出来的各个群标准差进行比较分析，查看改进后的K-means聚类算法得到的分群结果对比传统K-means聚类算法是否更密集，效果是否更优［16］。具体分群聚类效果分析如表6所示。

从表6可以看出，改进的K-means聚类算法使得电力客户数据分群聚类结果的所有平均客户群标准差都有显著减少，5个客户类的客户群标准差平均减少14.50%，这说明改进的K-means聚类算法使得电力客户分群聚类的各个客户群更为紧凑。特别地，居民客户的分群聚类结果中，所有客户群的标准差都减少了，减少率范围是4.88%～96.00%，明显改善了分群聚类的效果。其他4个客户类中虽然都会出现有一个客户群的标准差变差了，但是促使了其它客户群的标准差更显著地改善，从而保证了整体分群效果的紧凑性。改进的K-means聚类算法是通过牺牲原本比较松散的簇类为代价，以确保整体的聚类效果的改善［17］。而且，原本比较松散的的簇类本身就是比较模棱两可的簇类，很可能就是一个比较松散的群体，或者是噪声点、异常值之类的数据，故将密度大的簇类周边比较松散的电力客户数据对象划分到松散的群体，可以保证整体分群聚类效果的改进［18～19］。

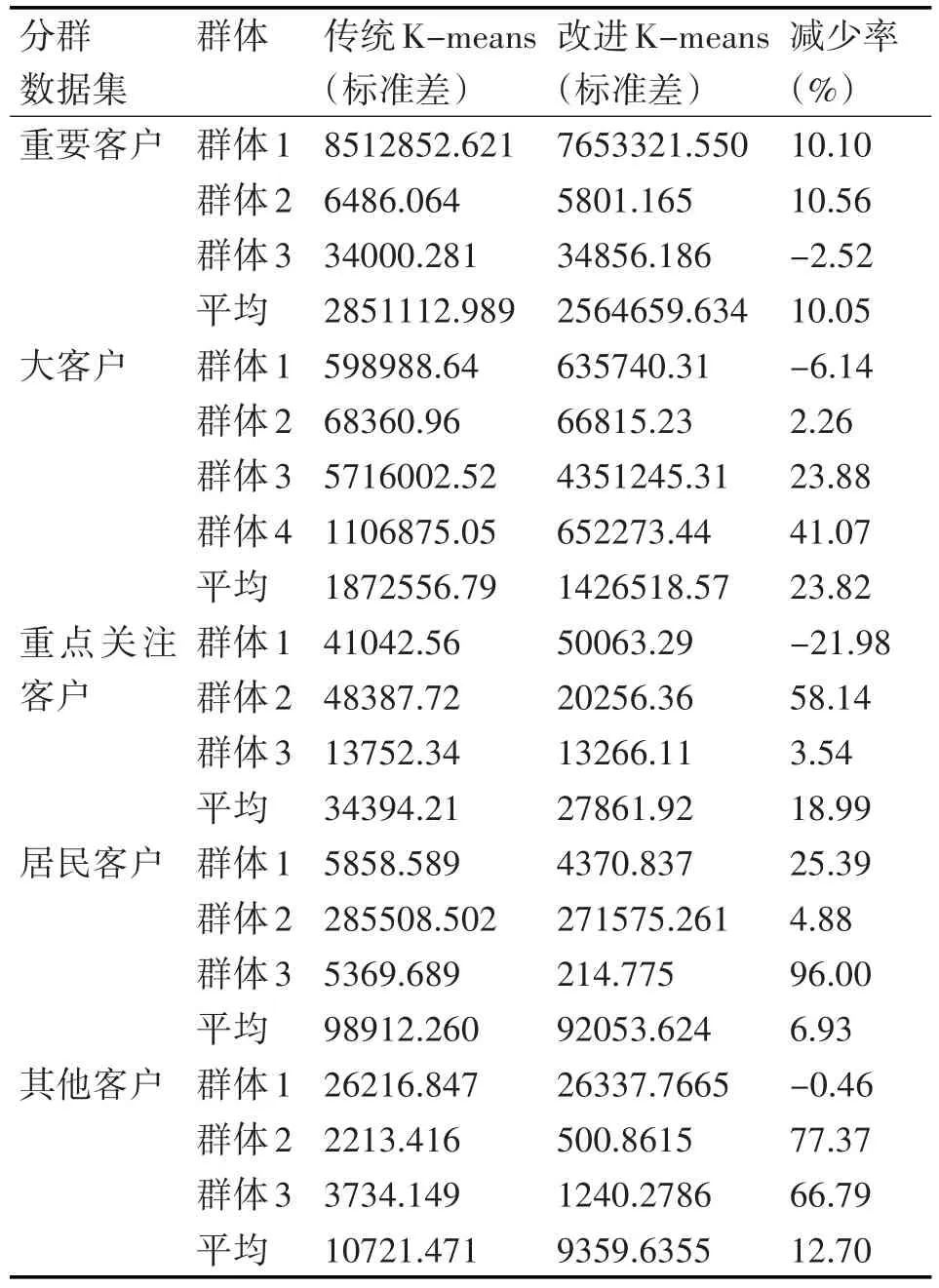
表6 传统聚类与改进聚类结果各群标准差比较

以上分析结果表明改进的K-means聚类算法显然更适合电力客户分群的实际情况。接着就可以对其聚类分群的结果进行进一步的解析。由于数据集在建模聚类之前使用了极差标准化的处理，这些标准化后的数据展现出来的聚类分群中心对观察数据来说是不够直观明了的。为了能够清晰明朗地观察聚类结果的情况，可以将最终的分群中心结果还原到了原始数据集量纲的状态下，进行分析各个客户类的分群聚类结果。

根据改进K-means聚类算法对电力客户分群聚类的结果与分析，销售和管理人员可以可以根据该分析结果，针对不同的客户群体实行差异化营销和服务策略，进而为企业的创造更多的价值。

5 结语

综上所述，本文采用的一种基于改进K-means聚类算法在电力客户价值分群上的聚类效果具有更高的准确度。该算法根据实际情况运用了改进的K-means聚类的准则函数，函数目标是使得加权的簇类标准差总和达到最小，而权重为各个簇类数据对象的个数占总体数据对象个数的比例，与该聚类准则函数相匹配的，同时也在聚类的迭代过程中加了权重，即使用了各个簇类的标准差开方后的倒数为距离的权重替代传统K-means聚类的直接计算欧氏距离的迭代过程。经研究验证，本文采用的改进K-means聚类算法在电力客户价值分群上聚类效果得到明显改善。下一步，可以在K-means聚类算法的初始聚类中心上做优化。

［1］卢建昌，樊围国.大数据时代下数据挖掘技术在电力企业中的应用［J］.广东电力，2014，27（9）：88-93.

LU Jianchang，FAN Weiguo.Application of data mining technology in electric power enterprisses in era of big data［J］.Guangdong Electric Power，2014，27（9）：88-93.

［2］李泓泽，郭森，王宝，等.基于遗传改进蚁群聚类算法的电力客户价值评价［J］.电网技术，2012，36（12）：256-261.

LI Hongze，GUO Sen，WANG Bao，et al.Evaluation on power customer value based on ants colony clustering algorithm optimized by genetic algorithm［J］.Power System Technology，2012，36（12）：256-261.

［3］李荟娆.K-means聚类方法的改进及其应用［D］.哈尔滨：东北农业大学，2014.

LI Huirao.Improved K-means clustering method and its application［D］.Harbin：Northeast Agricultural University，2014.

［4］张永晶.初始聚类中心优化的K-means改进算法［D］.吉林：东北师范大学，2013.

ZHANG Yongjing.Improved K-Means algorithm based on optimizing initial cluster centers［D］.Jinlin：Northeast Normal University，2013.

［5］翟东海，鱼江，高飞，等.最大距离法选取初始簇中心的K-means文本聚类算法的研究［J］.计算机应用研究，2014，31（3）：714-719.

ZHAI Donghai，YU Jiang，GAO Fei，et al.K-means text clustering algorithm based on initial cluster centers selection according to maximum distance［J］.Application Research of Computers，2014，31（3）：714-719.

［6］AGGARWALCC，LI Yan，WANG Jian-yong，et al.Frequent pattern mining with uncertain data［C］//Proc of the 15th ACM SIGKDD International Conference on Knowledge Discovery and Data Mining.New York：ACM Press，2009：29-38.

［7］郝拉娣，于化东.标准差与标准误［J］.编辑学报，2005，17（2）：116-118.

HAO Lati，YU Huadong.Standard deviation and standard error［J］.Acta Editologica，2005，17（2）：116-118.

［8］宋勇，陈贤富，姚海东.随机数发生器探讨及一种真随机数发生器实现［J］.计算机工程，2007（5）：71-73.

SONG Yong，CHEN Xianfu，YAO Haidong.Discussion on high-quality RNG and scheme of true RNG［J］.Computer Engineering，2007（5）：71-73.

［9］张宜浩，金澎，孙锐，等.基于改进k-means算法的中文词义归纳［J］.计算机应用，2012，32（5）：1332-1334.

ZHANG Yihao，JIN Peng，SUN Yue，et al.Chinese word sense induction based on improved k-means algorithm［J］.Journal of Computer Applications，2012，32（5）：1332-1334.

［10］张世博.基于优化初始中心点的K-means文本聚类算法［J］.计算机与数字工程，2011，39（10）：30-31.

ZHANG Shibo.AK-means text clustering algorithm based on optimizing initial points［J］.Computer&Digital Engineering，2011，39（10）：30-31.

［11］李应安.基于MapReduce的聚类算法的并行化研究［D］.广州：中山大学，2010.

LI Yingan.Research on parallelization of clustering algorithmbasedonmapReduce［D］.Guangdong：Sun Yat-sen University，SYSU，2010.

［12］宋亚奇，周国亮，朱永利，等.智能电网大数据处理技术现状与挑战［J］.电网技术，2013，37（4）：927-935.

SONG Yaqi，ZHOU Guoliang，ZHU Yongli，et al.Present status and challenges of big data processing in smart grid［J］.Power System Technology，2013，37（4）：927-935.

［13］李智勇，吴晶莹，吴为麟，等.基于自组织映射神经网络的电力用户负荷曲线聚类［J］.电力系统自动化，2008，32（15）：66-70.

LI Zhiyong，WU Jingying，WU Weilin，et al.Power customers load profile clustering using the SOM neural network［J］.Automation of Electric Power Systems，2008，32（15）：66-70.

［14］刘友波，刘俊勇，赵岩，等.基于多目标聚类的用电集群特征属性计算［J］.电力系统自动化，2009，33（19）：46-51.

LIU You，LIU Junyong，ZHAO Yan，et al.Present status and challenges of big data processing in smart grid［J］. Power System Technology，2009，33（19）：46-51.

［15］王锦，王会珍，张俐.基于维基百科类别的文本特征表示［J］.中文信息学报，2011，25（2）：27-31.

WANG Jin，WANG Huizhen，ZHANG Li.Text representation by the Wikipedia category［J］.Journal of Chinese Information Processing，2011，25（2）：27-31.

［16］何永秀，王冰，熊威，等.基于模糊综合评价的居民智能用电行为分析与互动机制设计［J］.电网技术，2012，36（10）：247-252.

HE Yongxiu，WANG Bin，XIU Wei，et al.Analysis of residents'smart electricity consumption behavior based on fuzzy synthetic evaluation and the design of interactive mechanism［J］.Power System Technology，2012，36（10）：247-252.

［17］索红光，王玉伟.一种用于文本聚类的改进k-means算法［J］.山东大学学报，2008，43（1）：60-64.

SUO Hongguang，WANG Yuwei.An improved k-means algorithm for document clustering［J］.Journal of Shandong University，2008，43（1）：60-64.

［18］王利朋，刘东权.基于粒子群算法的柔性形态学滤波器［J］.计算机应用，2010，30（10）：2811-2814.

WANG Lipeng，LIU Dongquan.Softmorphological filter based on particles warm algorithm［J］.Journal of Computer Applications，2010，30（10）：2811-2814.

［19］何径舟，王厚峰.基于特征选择和最大熵模型的汉语词义消歧［J］.软件学报，2010，21（6）：1287-1295.

HE Jingzhou，WANG Houfeng.Chinese word sense disambiguation based on maximum entropy model with feature selection［J］.Journal of Software，2010，21（6）：1287-1295.

Application of Improved K-means Clustering Algorithm in Clustering Based on Power Customer Value

ZHU ZhouWU Yang
（Information Center of Guizhou Power Grid Co.，Ltd，Guiyang550003）

This paper uses an improved criterion based on K-means clustering algorithm applied in electric power customer clustering research.According to the characteristics of electricity customers to implement different marketing strategies and provide differentiated services，accurate grouping of power customer need to be made.Traditional K-means clustering algorithm in data distribution uniform data of similar spherical agglomeration effect is better，once the unbalanced distribution density of data sets，class cluster size have significant difference，while the traditional K-means algorithm is easy to make thin categories carved up by high density small class clusters，resulting in electricity customer segmentation correct rate.This paper uses an improved K-means clustering algorithm based on the characteristics of the unbalanced data distribution of the actual power customers.Improved K-means algorithm puts up with a new weighting criteria，and modifies the clustering iterative process based on the criteria.The electricity customer data cluster results show that the improved K-means clustering algorithm and the cluster effect of each group of compactness can be improved effectively.The classification error conditions are improved obviously.

K-means algorithm，new clustering criterion，iterative weight，correct rate，standard deviation

TP391

10.3969/j.issn.1672-9722.2017.06.008

2016年12月15日，

2017年1月21日

朱州，男，博士，高级工程师，研究方向：电网信息化建设与数据分析管理。