基于非负矩阵分解的低秩矩阵恢复模型

徐梦珂许道云魏明俊

（1.贵州大学数学与统计学院贵阳550025）（2.贵州大学计算机科学与计算学院贵阳550025）

基于非负矩阵分解的低秩矩阵恢复模型

徐梦珂1许道云2魏明俊2

（1.贵州大学数学与统计学院贵阳550025）（2.贵州大学计算机科学与计算学院贵阳550025）

针对低秩矩阵恢复需要求解大规模矩阵核范数奇异值分解，计算复杂度高的缺陷，提出基于非负矩阵分解的低秩矩阵恢复模型。新模型通过对传统低秩矩阵恢复模型中的低秩矩阵进行非负因子分解，不但可以保持原始数据的局部特征，而且其低秩性可以快速求解矩阵低秩分解，从而避免了矩阵核范数求解大规模奇异值分解问题。在算法上采用多乘子交替迭代法（ADMM），将全局问题分解为多个易求解的局部子问题，对每个子问题利用拉格朗日乘子法分别对低秩矩阵和稀疏矩阵进行迭代求解。在ORL，AL_Gore和Windows三个图像数据库中Matlab仿真实验结果表明，新模型求解算法比传统低秩矩阵恢复模型识别率高，降秩效果明显，算法的时间复杂度低，从而提高算法运行速度。

非负矩阵分解；低秩矩阵恢复；多乘子交替迭代法；奇异值分解；图像识别

Class NumberTP391.41

1 引言

在大数据时代，如何高效率地处理大规模数据越来越受到人们重视。在现实生活中，巨大的数据量往往给数据分析带来麻烦，即所谓的“维度灾难”［1］。虽然许多数据都可以用矩阵形式表达，但是直接处理矩阵没有意义，矩阵分解就是将矩阵“分而治之”为数个矩阵的运算。非负矩阵分解是1999年由D.D.Lee和H.S.Seung首次提出，其基本思想是寻找一组基矩阵和线性组合参数来近似原始数据，同时约束表达基和参数都是非负的［2］。非负矩阵分解形式描述如下：

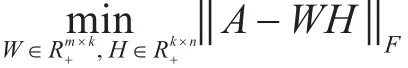
给定非负矩阵A∈Rm×n，k是所降的维度，求解最优化问题：其中W为基矩阵，W各列表示原始数据的潜在结构，具有稀疏性。H为系数矩阵，H各列表示各个结构在该原始数据中所占的比重。‖‖AF是Frobenius范数：

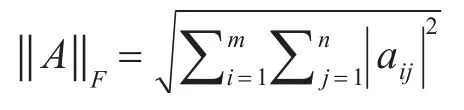
一方面，矩阵进行非负矩阵分解后，其低秩和稀疏性使得算法速度快；另一方面，现实中的很多物理特性都是非负的，负数没有实际意义，非负约束使得模型具有很强的可解释性。

对非负矩阵分解的算法有很多，大体上分为两类，一类是公式逼近法，优点是迭代公式构造简单，主要的运算是矩阵之间加法、乘法和求逆等，但收敛性难以得到证明［3］。另一类是优化逼近法，如梯度投影法、二次规划序列逼近法等，优点是算法都比较成熟，但是只能保证解的局部最优性，因此仍然需要对算法进行改进［4～5］。

更具挑战的是一些大规模数据可能含有空缺或者毁损元素。主成分分析法是利用K-L变换将原始数据投影到一个低维特征空间，提取主要特征［6］，该方法可以用在人脸识别中。然而实际中，人脸图像是一个二维矩阵，主成分分析把矩阵变成向量，破坏了矩阵的空间结构，其性能对于有噪声的情况缺乏鲁棒性。2011年John Wright等提出来的低秩矩阵恢复解决了上述问题［7］。低秩矩阵恢复把向量的稀疏表示推广到矩阵的低秩情形，将含有噪音的数据矩阵表示为低秩矩阵与稀疏噪声矩阵之和，再通过求解矩阵核范数优化问题从含“噪音”原始矩阵中恢复出“干净”的低秩矩阵。同时，求解低秩矩阵近似的一系列算法研究也在积极展开。

2009年，Beck，Teboulle用迭代阈值算法来求解矩阵核范数最小化问题［8］，2010年Cai、Candes、and Shen提出了奇异值阈值算法，在求矩阵奇异值时用软阈值算子代替，该算法仅对于秩比较低的矩阵有效［9］。Lin、Chen and Wu提出用增广拉格朗日乘子法求解低秩矩阵恢复，增广拉格朗日乘子法比前面的算法速度快［10］。但是以上算法每一步迭代都要求解核范数奇异值分解问题，如果矩阵大小是n×n时，它的奇异值计算时间复杂度是O(n3)，所以当矩阵规模比较大时，这些算法计算复杂度会比较高，因此如何有效处理矩阵核范数奇异值分解是个难点。

非负矩阵分解通过对矩阵进行非负因子分解，能够快速求解矩阵的低秩分解，从而可以避免矩阵核范数求解大规模奇异值分解问题。因此，受到非负矩阵分解的启发，本文研究如何提高低秩矩阵恢复的鲁棒性，采用低秩矩阵的非负矩阵分解技术，提出基于非负矩阵分解的低秩矩阵恢复模型，新模型不但可以保持原始数据的局部特征，而且避免求解矩阵核范数大规模奇异值分解问题，从而降低时间复杂度。在算法方面，由于基于非负矩阵分解的低秩矩阵恢复模型涉及到多个变量，所以采用多乘子交替迭代算法，将变量求解分成多个子问题，固定其他子问题，交替最小化求解每一个子问题的增广拉格朗日函数。基于非负矩阵分解的低秩矩阵恢复模型求解与传统的低秩矩阵恢复模型在ORL，AL_Gore和Windows三个图像数据库的应用结果相比，提高了图像的识别率和低秩矩阵的降秩能力，降低了时间复杂度，加快了算法的运行速度，进而表明了低秩矩阵恢复的非负矩阵分解技术的有效性。

2 基于非负矩阵分解的低秩矩阵恢复模型

矩阵低秩近似把压缩感知理论通过一维向量拓展到二维矩阵上。矩阵的稀疏性分为两类：矩阵元素的稀疏性和矩阵奇异值的稀疏性。元素的稀疏性指矩阵非零元素个数比较少；矩阵奇异值的稀疏性指矩阵奇异值非零元素个数比较少。若同时考虑矩阵元素和奇异值的稀疏性，可以得到低秩矩阵恢复模型。低秩矩阵恢复模型描述如下［2］

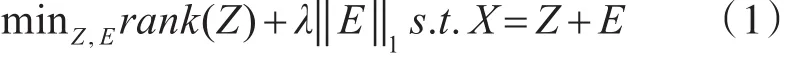
其中X∈Rm×n是数据矩阵，Z∈Rm×n是低秩矩阵，Z的秩rank(Z)=r，r＜＜min(m，n)，E∈Rm×n是稀疏噪音矩阵。低秩矩阵恢复解决了这样一个问题：假设原始数据含有噪音，就将含有噪音的数据矩阵表示为低秩矩阵与稀疏噪声矩阵之和，再通过求解矩阵核范数优化问题从含有“缺损”数据矩阵中恢复“干净”的低秩矩阵。

然而矩阵秩的估计问题是NP难的，关键问题是，如何处理矩阵的秩？Candes和Recht从理论上解决了这个问题：如果一个矩阵的秩足够小，类比压缩感知中的l0范数和l1范数，自然而然把矩阵的秩用矩阵核范数来代替，从而转化为核范数的最小化问题［11］。设矩阵A∈Rm×n，则矩阵核范数‖‖A*：，即矩阵奇异值之和。

核范数是凸的，最小化核范数就是一个凸优化问题。2011年Emmanuel和Candes在文献［7］给出了矩阵秩问题如何转化为矩阵核范数凸优化问题的证明，即下面定理1和2。

定理1［7］假设矩阵A0∈Rm×n（m≥n），如果存在参数μ＞0，有：

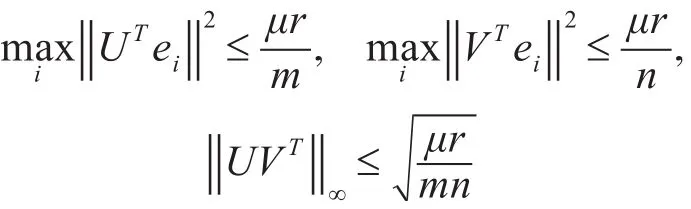
则称A0以参数μ满足非相干性条件。

其中ei是单位向量，矩阵A0的奇异值分解为是矩阵A0的秩，范数

定理2［7］在非相干性条件下，从一个秩为r的矩阵A0中均匀抽取m个元素，满足：，则核范数最小化问题的最优解Aˉ依至少1-cn-3的概率接近原来矩阵A0，其中C，c是常数。

但是很多求解低秩矩阵恢复模型的算法每一步迭代都要求解核范数奇异值分解问题，当矩阵大小是m×n时，它的奇异值分解时间复杂度是O(n3)，所以考虑到当矩阵规模比较大时，以上这些算法时间复杂度会比较高。因此，基于非负矩阵分解是通过对矩阵进行非负因子分解，能够快速求解矩阵低秩分解的想法，本文采用低秩矩阵的非负分解技术，提出基于非负矩阵分解的低秩矩阵恢复模型，其数学表达式如下：

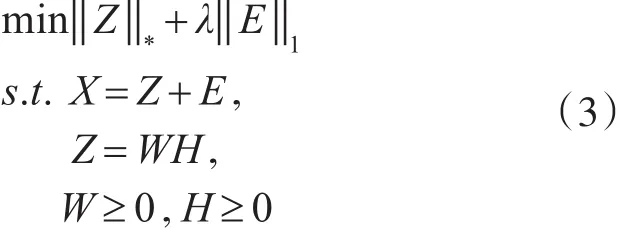
X∈Rm×n是原始数据矩阵，Z∈Rm×n是低秩矩阵，E∈Rm×n是稀疏噪音矩阵，是Z的非负因子。通过把非负矩阵分解运用到低秩矩阵恢复中，不但可以保持原始数据的局部特征，而且避免求解大规模矩阵核范数的奇异值分解问题，从而对原始数据矩阵进行降秩，降低算法的时间复杂度，提高算法运行速度。

3 基于非负矩阵分解的低秩矩阵恢复模型求解

由于基于非负矩阵分解的低秩矩阵恢复模型涉及到多个变量，所以本文用多乘子交替迭代算法来求解目标函数［12］，其增广拉格朗日函数表示为［10］：

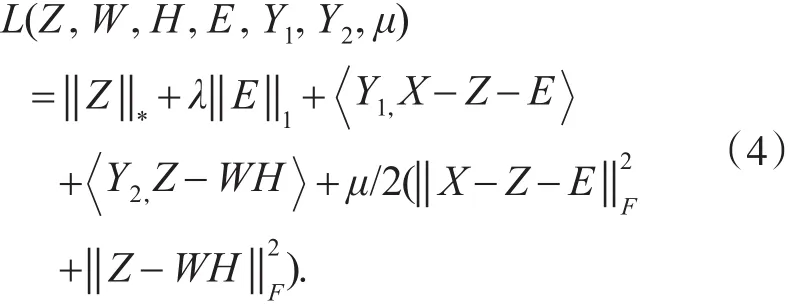
其中X∈Rm×n是原始数据矩阵，Z∈Rm×n是低秩矩阵，E∈Rm×n是稀疏噪音矩阵，是Z的非负因子，为两个拉格朗日乘子，μ＞0为惩罚因子，A，B表示矩阵的内积，增广拉格朗日函数消除了等式约束，在函数里同时增加一次惩罚项和二次惩罚项，采用迭代方法可求得函数解和拉格朗日乘子。

交替迭代求解各个子问题：

1）首先固定其他变量，求解子问题Z，Z的增广拉格朗日函数表示如下

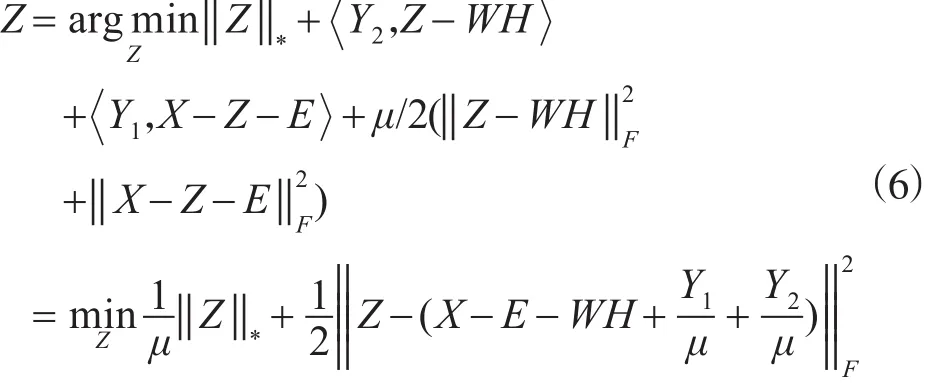
对Z的求解会用到核范数的次微分，通过文献［13］，Z的最优解Z*的求解可以通过奇异值收缩得到如下的闭式解：

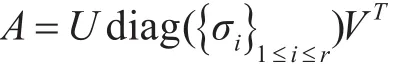
那么可以得到：

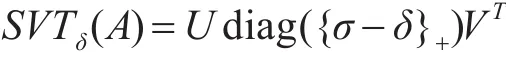
其中(σ-δ)+=max(0，σ-δ)。

所以Z的最优解Z*的求解式（7）可以转化成：2）固定其他变量，求解子问题E，求解E有下面的优化模型：

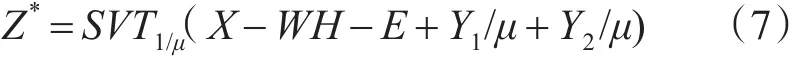
为了方便计算以及简化符号，设A=X-WH-E+Y1/μ+Y2/μ，δ=1/μ。

即Z*=SVTδ(A)。

由于矩阵A的SVD分解为

根据文献［14］，该模型有如下闭式解：

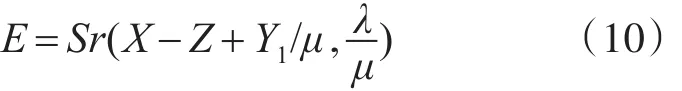
其中[，]:，i矩阵的第i列且bi指矩阵的第i列。

3）固定其他变量，求解子问题W和H：

对W和H求解是最小二乘优化问题［15］，让D=Z+Y2/μ，当固定变量H时，W=DHT，根据文献［15］，本文设计如下迭代：

其中QR(DHT)表示通过QR分解得到矩阵DHT的一个正交基的操作。

当固定变量W，H=WTD，同理，对H的迭代如下：

4）对拉格朗日乘子的更新：

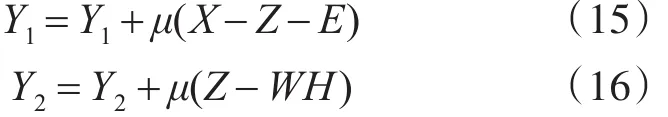
综上所述，基于非负矩阵分解的低秩矩阵恢复模型求解算法步骤如下：

输入原始数据：X∈Rm×n。

初始化：Z=0，E=0，W=0，H=eye(m，n)，Y1=0，Y2=0，μ。

输出：Z，E

步骤：（1）根据式（8）更新Z；

（2）根据式（10）更新E；

（3）根据式（13）更新W；

（4）根据式（14）更新H；

（5）根据式（15）（16）更新拉格朗日乘子Y1，Y2；

（6）更新惩罚因子μ；

（7）迭代停止条件：

重复1～7，直到停止迭代，返回Z和E。

4 数值实验及分析

4.1 算法复杂度分析

首先对基于非负矩阵分解的低秩矩阵恢复模型求解算法进行时间复杂度分析：因为该模型求解的主要算法包括：低秩矩阵Z∈Rm×n的奇异值分解，求解非负因子W、H的QR分解和一些矩阵乘法计算这三个主要部分。其中Z的秩rank(Z)=r，r＜＜min(m，n)。

低秩矩阵Z奇异值分解时间复杂度是：O(r3)；QR分解时间复杂度为O(mr2+nr2)；其余一些矩阵乘法所需时间复杂度为O(rmn)；所以基于非负矩阵分解的低秩矩阵恢复模型算法总的时间复杂度为O(r3+r2(m+n)++rmn)。

低秩矩阵恢复算法主要是求解原始矩阵的奇异值分解，时间复杂度是O(m3)或者是O(n3)，都远远大于基于非负矩阵分解的低秩矩阵恢复模型算法的时间复杂度O(r3+r2(m+n)++rmn)，因此基于非负矩阵分解的低秩矩阵恢复模型算法求解的时间复杂度比传统低秩矩阵恢复模型要低。

4.2 数值实验及分析

本文从ORL，AL_Gore和Windows三个图像数据库中分别随机选取10张图像作为样本进行Matlab数值实验，分别把传统模型的交替迭代方法（ADM）和基于非负矩阵分解的低秩矩阵恢复模型的多乘子交替迭代法（ADMM）来作为实验对比。交替迭代方法是解决凸优化问题的增广拉格朗日函数法的进一步改进。在偏微分方程中，对于结构型变分不等式，增广拉格朗日求解没有充分利用结构型变分不等式可分离特性，为此Gabay和Mercier［16］首先提出了交替迭代方向法，其思想是先求解一个子变分不等式问题得到一个解x，再利用新的迭代点x去求解另一个子变分不等式得到迭代点y，最后用x、y去迭代拉格朗日乘子。

在基于非负矩阵分解的低秩矩阵恢复模型实验中，本文设正则参数λ=0.03，惩罚因子原始数据X的所有元素

绝对值的平均值。采用算法恢复矩阵与原始矩阵的误差作为识别率，其定义如下

其中，X∈Rm×n是原始数据矩阵，Z∈Rm×n是低秩矩阵，E∈Rm×n是稀疏噪音矩阵。

首先在400张ORL人脸数据库中随机选取10幅56×56原始数据图像X，分别从原始数据矩阵X得到低秩矩阵Z的降秩效果，算法运行时间和所恢复矩阵的识别率这三个方面，对传统低秩矩阵恢复模型的交替迭代法（ADM）和基于非负矩阵分解的低秩矩阵恢复模型的多乘子交替迭代法（ADMM）的实验结果进行对比，结果如表1所示。

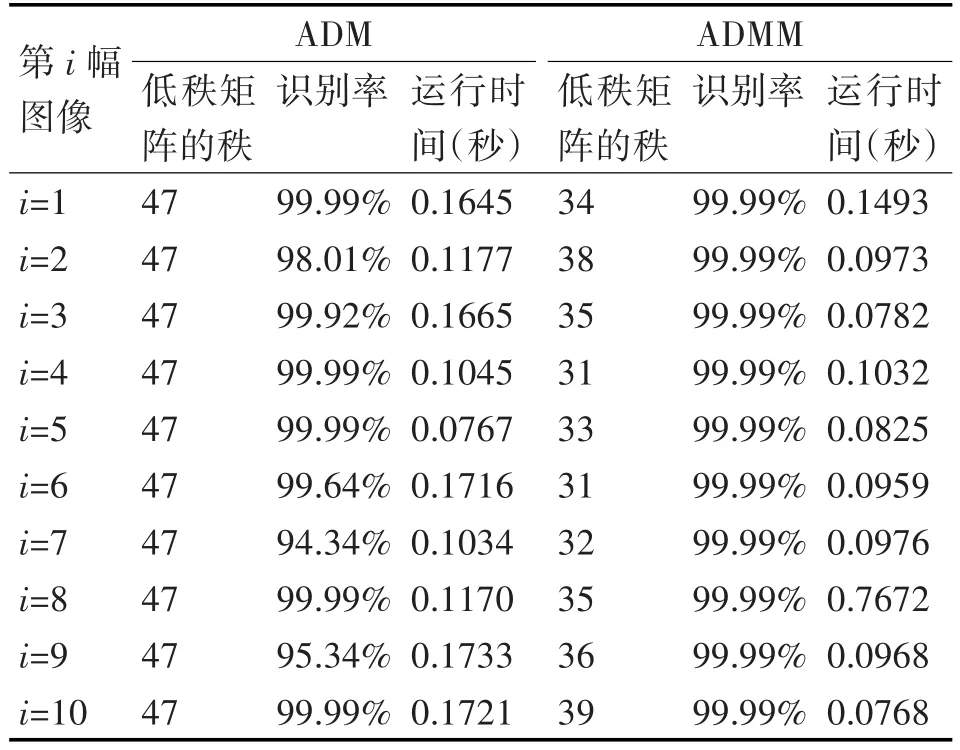
表1 ORL数据库ADM和ADMM实验结果比较

为了更好地验证本文所提算法的有效性，再次在140张AL_Gore人脸数据库中随机选取10幅107×107原始数据图像X进行实验，结果如表2所示。

为了验证新模型的ADMM算法对大数据的降秩效果，本文在18张AL_Gore数据库中随机选取10幅大小为1200×1600的图像，为了方便实验，把图像规模预处理为1200×1200的原始图像X进行实验，结果如表3所示。

从表1，表2和表3比较结果可以得出：本文提出的基于非负矩阵分解的低秩矩阵恢复模型比传统的低秩矩阵恢复模型求解算法不仅仅识别率高，时间复杂度低，运行时间短，而且可以明显地降低原始矩阵的秩。

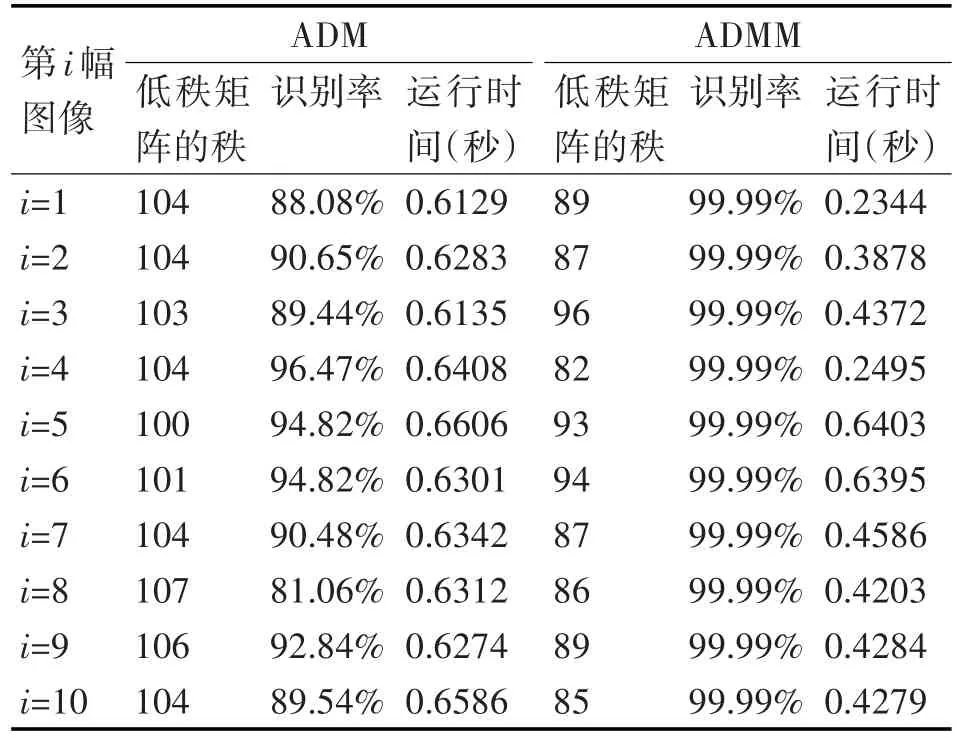
表2 AL-Gore数据库ADM和ADMM实验结果比较

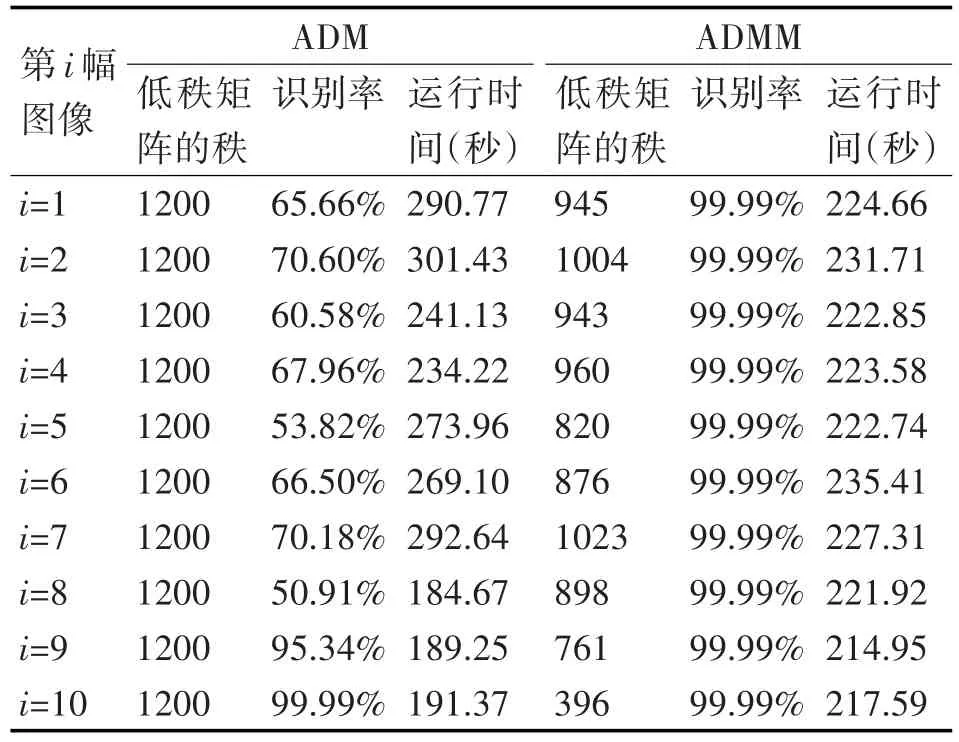
表3 Windows数据库ADM和ADMM实验结果比较

为了比较出算法对不同秩的原始数据X矩阵的降秩效果，任意选取了6幅秩不等的图像矩阵X，把基于非负矩阵分解的低秩矩阵恢复模型的ADMM算法，传统低秩矩阵恢复模型的ADM算法和利用梯度下降来求低秩和稀疏矩阵方法的近端梯度算法（APG）进行比较，结果如图1，从图中可以得出：随着原始数据矩阵秩的增加，基于非负矩阵分解的低秩矩阵恢复模型的ADMM算法降秩效果最明显，而ADM算法降秩效果不佳。

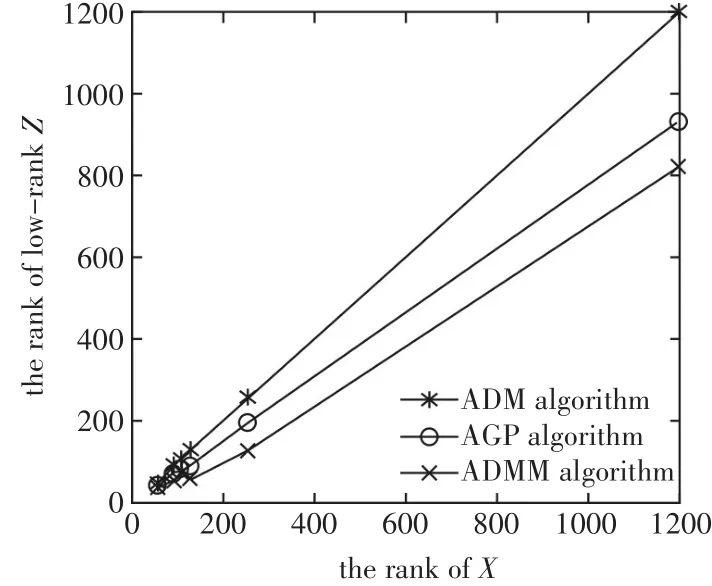
图1 ADM，ADMM，APG算法对不同维数的原始数据降维效果

最后，本文把基于非负矩阵分解的低秩矩阵恢复模型的ADMM算法和传统低秩矩阵恢复模型的ADM算法的识别率进行比较，结果如图2。

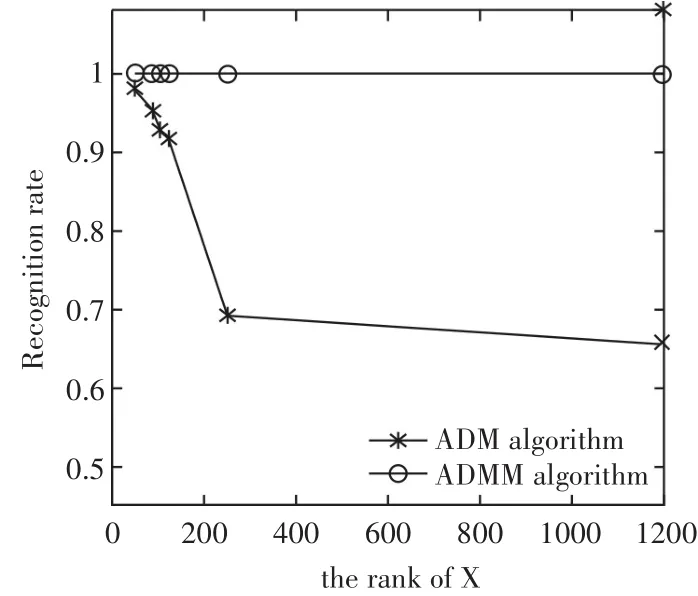
图2 ADM，ADMM算法的识别率比较

从图2可以得出：随着原始数据矩阵的秩的增加，基于非负矩阵分解的低秩矩阵恢复模型的ADMM算法识别率高，而ADM算法识别率逐渐降低。

5 结语

低秩矩阵恢复是重要的数据分析工具，低秩特性解决了大规模数据效率问题，稀疏捕捉了大数据中的关键信息，两者抓住了主要矛盾问题，是处理大数据的核心技术，在人脸识别、推荐系统等领域有了不少的应用。本论文观察到矩阵分解的低秩性可以降低算法的时间复杂度，因此把非负矩阵分解的思想加入到低秩矩阵恢复模型中，采用把低秩矩阵部分进行非负矩阵分解技术，不但可以得到原始数据的局部特征，避免了求解大规模矩阵核范数的奇异值分解，从而达到降秩效果在算法上采用了多乘子交替迭代算法框架，降低了时间复杂度，从而提高算法的运行速度，而且矩阵分解结果不含负值元素，具有实际意义。本论文进一步改进是：1）进一步挖掘大规模数据的潜在结构如正定性，结构稀疏性等，从而提高矩阵恢复的识别率。2）算法迭代求解非负因子W，H过程中，考虑如何更加有效地处理负元素，进一步去提高算法精度。

［1］David L，Donoho.High-dimensional data analysis：the cures and blessings of dimensionality［C］//Proc.Amer. Math Soc.Conf.Math Challenges Lecture，2000.

［2］Daniel D，Lee H，Sebastians.Learning the parts of objects by non-negative matrix factorization［J］.Nature，1999，

（401）：788-791.

［3］JIANG J.Improvement of non-negative matrix decomposition methods and its applications［D］.Beijing：Beijing University of Techology，2011：1-60.

［4］张可村，李换琴.工程优化方法及其应用［M］.西安：西安交通大学出版社，2007：83-156.

ZHANG Kecun，LI Huanqin.Engineering optimization method and its application［M］.Xi'an：Xi'an Jiaotong University Press，2007：83-156.

［5］阳明盛，罗长童.最优原理、方法及求解软件［M］.北京：科学出版社，2006：46-132.

YANG Mingsheng，LUO Changtong.Best principles，methods and software［M］.Beijing：Science Press，2006：46-132.

［6］Hotelling H.Analysis of a complex of statistical variables into principal components［J］.Journal of Educational Psychology，1933，24：417-441.

［7］Candes E，Li X，Ma Y，Wright J.Robust principal component analysis？［J］.Journal of ACM，2011，58（3）：1-37.

［8］Beck A，Teboulle M.A fast iterative shrinkage thresholding algorithm for linear inverse problems［J］.SIAM Journal on Imaging Sciences，2009，2（1）：183-202.

［9］Cai J，Candes E，Shen Z.A singular value thresholding algorithm for matrix completion［J］.SIAM Journal on Optimization 2010，20（4）：1956-1982.

［10］Lin Z，Chen M，Wu L.The augmented Lagrange multiplier method for exact recovery of corrupted low-rank matrices［C］//In Technical Report UILU ENG，2009.

［11］Candes E，Recht B.Exact matrix competion via convex optimization［J］.Foundation of Computational Math，2009，9（6）：717-772.

［12］XIAO M，JUN F.Sparse and low-rank matrix decomposition via alternation direction methods［J］.Pacific Journal of Optimization，2013，9（1）：167-180.

［13］Cai J，Emmanuel J，Candes.A singular value thresholding algorithm for matrix completion［J］.SIAM，2010，1956-1982.

［14］Liu Y，Jiao L，Sheng F.A fast tri-factorization method for low-rank matrix recovery and completion［J］.Pattern Recognition，2013，46（1）：163-173.

［15］Yuan S，Zai W，Yin Z.Augmenteed lagrangian alternating direction method for matrix separation based on low-rank factorization［J］.Optimization method and Software，2014，29（2）：239-263.

［16］Gabay D，Mercier B.A dual algorithm for the solution of nonlinear variational problems via finite elements approximations［J］.Compute Math Appl，1976（2）：178-40.

Low-rank Matrix Recovery Model Based on Non-negative Matrix Factorization

XU Mengke1XU Daoyun2WEI Mingjun2
（1.College of Mathematics and Statistics，Guizhou University，Guiyang550025）（2.College of Computer Science and Technology，Guizhou University，Guiyang550025）

To overcome the shortage of large-scale nuclear matrix singular value decomposition existing in low-rank matrix recovery model，the paper proposed low-rank matrix recovery model based on non-negative matrix factorization.Non-negative matrix factorization（NMF）applied to the low-rank matrix，which could quickly deal with the problem of the decomposition matrix of low-rank and avoid large-scale nuclear matrix singular value decomposition.Then the algorithm used alternarting directions method of multipliers（ADMM）.ADMM divided the global problem into partial sub-problems.Each sub-problem used Lagrange multipliers to solve low rank matrix and sparse matrix.Experimental results in ORL，AL_Gore and Windows databases showed that low-rank recovery model based NMF has higher recognition rate，better reduction rank and lower the complexity of the algorithm than other traditional low-rank recovery model.

non-negative matrix factorization（NMF），low-rank matrix recovery，alternating directions method of multipliers，singular value decomposition（SVD），image recognition

TP391.41

10.3969/j.issn.1672-9722.2017.06.002

2016年12月18日，

2017年1月25日

国家自然科学基金项目（编号：61262006，61540050）；贵州省重大应用基础研究项目（编号：黔科合JZ字［2014］2001）；贵州省科技厅联合基金（编号：黔科合LH字［2014］7636）资助。

徐梦珂，女，硕士研究生，研究方向：密码学理论与工程。许道云，男，博士，教授，研究方向：可计算性与计算复杂性、算法设计与分析。魏明俊，男，硕士研究生，研究方向：可计算性与计算复杂性。