一道数学课本好习题的使用有感

云南省孟连县民族中学 赵力珊

初中数学教课书中，许多习题都具有很广泛的应用价值，用好教科书里的练习，绝大多数学生都能够达到教学要求，一些学有余力的学生，也能在教科书的练习中得到很大的提升空间。认真研究课本习题的应用，不仅可以很好地学好基础知识，而且有利于培养学生的应用意识，提供思维水平，提升解题能力。

人教版教材《初中数学八年级下》60页的习题第6题，采用“一题多解”将菱形的判定方法一网打尽，也将平行四边形的判定也一网打尽了。让学生经历从不同角度寻求分析问题和解决问题的方法的过程，体验了解决问题方法的多样性。是一道值得妙用的好习题。

原题目：6.如图，AE∥BF，AC平分∠BAD，且交BF于点C，BD平分∠ABC，且交AE于点D，连接CD。求证：四边形ABCD是菱形.

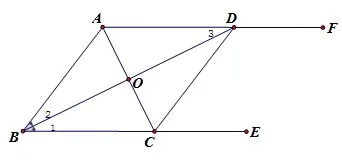
方法一：用定义证明，即有一组邻边相等的平行四边形叫做菱形。

证明：∵BD平分∠ABC

∴∠1=∠2

∵AE∥BF

∴∠1=∠3

∴∠2=∠3

∴AB=AD

同理：AB=BC

∴AD=BC

∵AE∥BF即AD∥BC

∴四边形ABCD是平行四边形

∵AB=AD

∴四边形ABCD是菱形

方法二：用判定定理1“对角线互相垂直的平行四边形是菱形”证明。

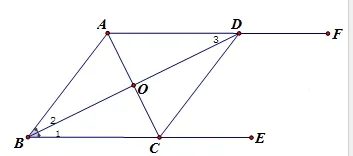
证明：∵BD平分∠ABC

∴∠1=∠2

∵AE∥BF

∴∠1=∠3

∴∠2=∠3

∴AB=AD

同理：AB=BC

∴AD=BC

∵AE∥BF即AD∥BC

∴四边形ABCD是平行四边形

∵AB=AD AC平分∠BAD

∴AC⊥BD

∴四边形ABCD是菱形

方法三：用判定定理2“四条边相等的四边形是菱形”证明。

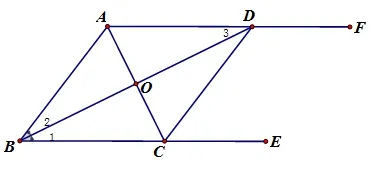
证明：∵BD平分∠ABC

∴∠1=∠2

∵AE∥BF

∴∠1=∠3

∴∠2=∠3

∴AB=AD

同理：AB=BC

∴AB=AD=BC

∵AB=AD AC平分∠BAD

∴OB=OD AC⊥BD

∵ AC⊥BD

∴∠BOC=∠DOC=90°

在△BOC和△DOC中

∴△BOC≌△DOC（SAS）

∴BC=CD

∴AB=AD=BC=CD

∴四边形ABCD是菱形

在上述证明中，我们先得出“AD=BC且AD∥BC”，再证明四边形ABCD是平行四边形。实际上，还可以引导学生发现：

（1）可以先得到“AD=BC，AB=CD”，再证明四边形ABCD是平行四边形。

（2）可以先得到“OB=OD，OA=OC”，在证明四边形ABCD是平行四边形。

（3）也可以用“A D∥B C，AB∥CD” 证明四边形ABCD是平行四边形。

（4）甚至可以先证明“∠BAD=∠BCD，∠ABC=∠ADC”，再证明四边形ABCD是平行四边形。

也就是说，这道题不仅训练学生对菱形的判定的灵活使用，也可以训练学生巩固平行四边形的各种判定。“一题多解”的功效不言而喻。

所谓“一题多解”，就是从不同的角度，不同的方位审视分析同一题中的数量关系，用不同解法求得相同结果的思维过程。《数学课程标准（2011年版）明确要求要让学生“经历从不同角度寻求分析问题和解决问题的方法的过程，体验解决问题方法的多样性，掌握分析问题和解决问题的一些基本方法。”

课本中这样的好题的还很多。深入研究教材的典型练习，能帮助学生走出题海，做一题，会一类，通一片，达到事半功倍的效果。从而提高课堂教学的质量和效率。