脉冲超宽带测控信号时延精密跟踪方法*

廉 昕

(装备学院 光电装备系，北京 101416)



脉冲超宽带测控信号时延精密跟踪方法*

廉 昕**

(装备学院 光电装备系，北京 101416)

脉冲超宽带测控新体制可有效提高测控系统的安全性能，且具有潜在的高精度测距能力。为了实现其高精度测距功能，提出了一种基于延迟锁定环路的脉冲超宽带测控信号时延精密跟踪方法。该方法在传统伪码跟踪环的基础上进行改进，利用基于非相干积分的非线性反馈环路对接收信号的脉冲相位进行精密跟踪。理论分析和仿真结果表明，该延迟锁定环路可以完成对脉冲超宽带测控信号的时延精密跟踪。与直扩测控信号相比，在相同条件下，脉冲超宽带测控信号的时延跟踪相对误差更大，但由于脉冲宽度很窄，在一定载噪比条件下，其测量精度仍可达厘米量级甚至更高。

脉冲超宽带；测控；时延跟踪；延迟锁定环；高精度测距

1 引 言

随着航天技术的不断进步，世界各国纷纷致力于航天事业的发展，未来在航天领域的竞争将日趋激烈，航天测控通信系统面临的电磁环境也会更加复杂。为了提高我国航天测控系统的安全性和抗干扰能力，文献[1-2]引入脉冲超宽带技术，提出了脉冲超宽带测控新体制。它利用宽度为纳秒级的窄脉冲作为数据传输的载体，具有隐蔽性好、抗干扰能力强、测距精度高等诸多优点，是一种极具发展潜力的测控新体制。

信号同步是测控系统的核心环节，决定着系统的测量精度，同时也是后续数据解调的基础。对于脉冲超宽带测控系统，信号同步同样分为捕获与跟踪两个阶段。在信号捕获阶段，已对接收信号的伪码相位和脉冲相位进行了粗同步，可将同步误差控制在半个脉冲宽度之内，而对接收信号脉冲相位的进一步精密跟踪则决定了系统最终的测距精度。

目前，脉冲超宽带系统主要用于室内短距离的高速数据传输和高精度测距定位，其信号同步方法主要有基于相关检测的方法和基于估计理论的方法，前者的同步精度受采样率制约，而后者的同步精度较低，且两者均未考虑接收信号的动态变化[3-5]。在脉冲超宽带测控系统中，收发两端之间的相对运动会导致接收信号时延相位发生时变动态变化，这给信号时延的精密跟踪带来了困难。

本文针对脉冲超宽带测控信号，提出基于延迟锁定环路的脉冲相位跟踪方法，对接收信号的时延进行精密跟踪，以实现高精度测距功能。

2 系统框架

延迟锁定环路是直接扩频测控系统中通常采用的伪码跟踪方法。其基本原理与锁相环类似，也是利用一个非线性反馈环路来实现对伪码相位的精细同步。鉴于脉冲超宽带测控信号与直扩信号的相似性，本文利用延迟锁定环路对脉冲超宽带测控信号的脉冲相位进行精密跟踪，其结构框图如图1所示[6-8]。

延迟锁定环路主要由鉴别器、环路滤波器、压控振荡器(Voltage Controlled Oscillator,VCO)、本地信号发生器等组成。首先本地载波NCO产生正交载波信号，对接收信号r(t)进行正交下变频和低通滤波处理，得到rI(t)、rQ(t)两路基带信号。本地信号发生器根据信号时延(伪码相位和脉冲相位)捕获结果产生超前、滞后两路本地信号sE(t)、sL(t)，两者的时延相位均与时延捕获结果相差(超前或滞后)半个脉冲宽度。将本地信号sE(t)、sL(t)分别与接收信号rI(t)、rQ(t)进行相关运算，并进行积分清洗。之后将4路结果输入到鉴别器中，采用一定的鉴别算法进行脉冲相位鉴别，得到误差信号et。再经过环路滤波器得到控制电压信号来控制压控振荡器的输出，以调整本地信号产生时钟，使得本地对准支路信号sP(t)的脉冲相位逐渐接近接收信号，直至两者差值为零，即实现了本地信号对接收信号脉冲相位的精确同步。最终对准支路输出sP(t)即为同步跟踪结果。

3 数学模型

脉冲超宽带测控系统接收信号的表达式为

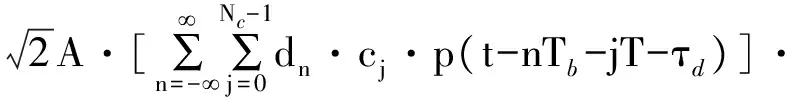
(1)

n(t)=nI(t)cos[2π(fc+fd)t+φ]- nQ(t)sin[2π(fc+fd)t+φ]。

(2)

式中:nI(t)和nQ(t)为n(t)的两个正交分量，两者相互独立，均值均为0，双边功率谱密度均为N0/2。

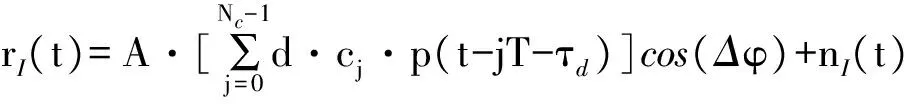
(3)

(4)

式中:Δφ为载波残余相位。

而本地根据时延捕获结果产生的超前支路和滞后支路信号分别为

(5)

(6)

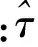
将rI(t)、rQ(t)分别与超前、滞后两支路本地信号进行相关运算和积分清洗，积分时间设为1个伪码周期，对应采样点数为N。由于伪码捕获已完成，本地信号与接收信号的伪码码元序列完全对齐，两者乘积为1，则4路积分清洗结果分别为

(7)

(8)

(9)

(10)

将以上4路相关结果送入环路鉴别器，这里选用的鉴别算法为超前滞后能量差法[10-12]，即计算滞后支路相关结果的能量与超前支路相关结果能量之差，得到误差信号

(11)

式中:ne(ti)为鉴别器输出噪声项。

定义鉴别器的鉴别特性曲线函数为

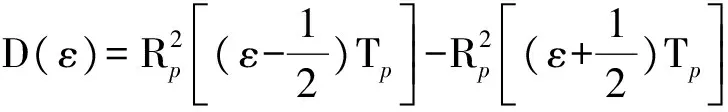
(12)

式中:ε=Δτ/Tp为相对时延跟踪误差。

由式(11)和式(12)可知，误差信号e(ti)与D(ε)呈线性关系，当噪声项为0时，e(t)与D(ε)成正比。而单脉冲信号的归一化自相关函数Rp(τ)为

(13)

代入到式(12)中即可得到鉴别特性函数D(ε)的表达式为

(14)

该鉴别特性曲线如图2所示。

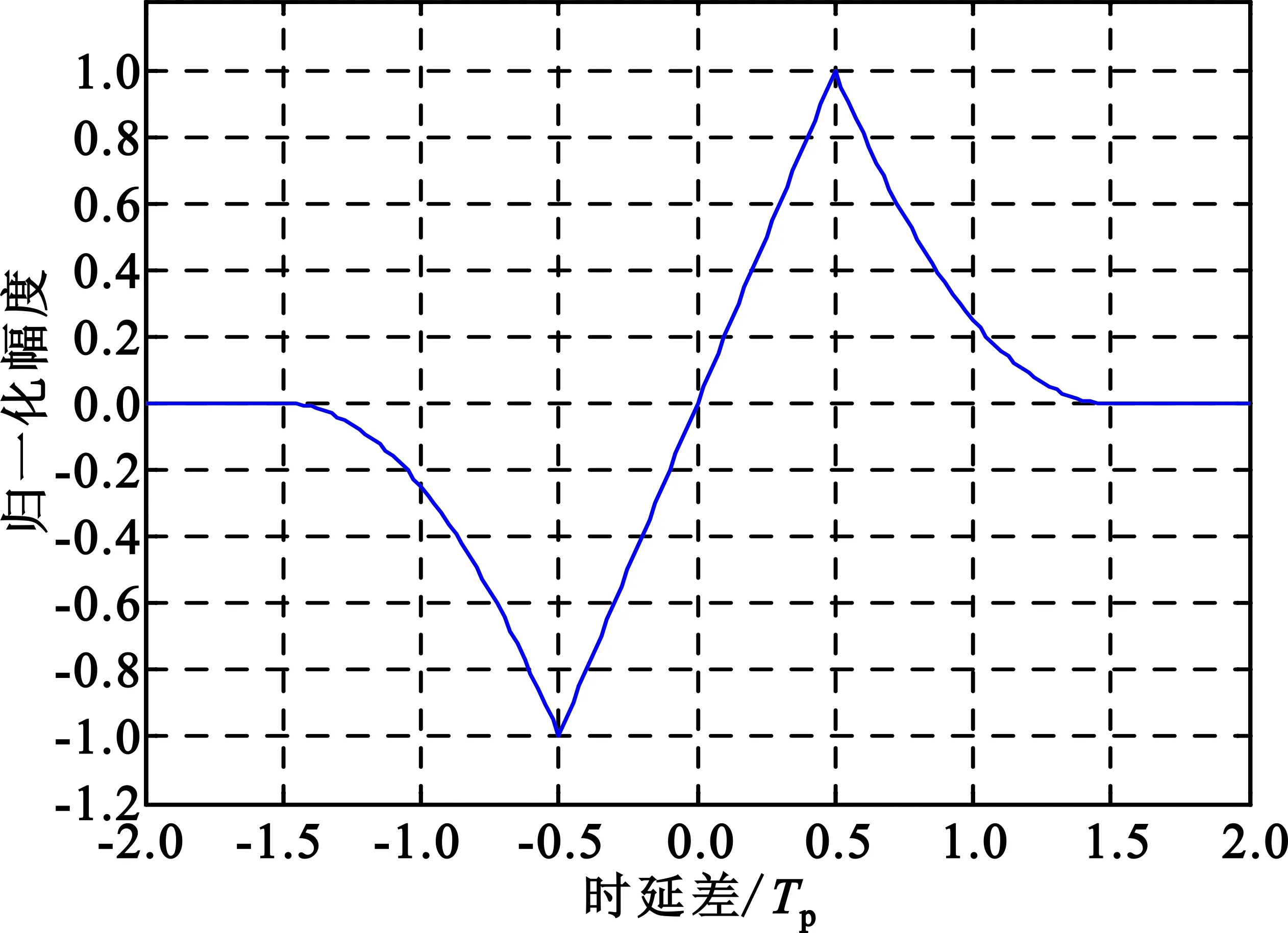
图2 延迟锁定环理论鉴别特性曲线

可见，鉴别器的理论鉴别特性曲线在(-0.5,0.5)区间内呈线性，其斜率为2。则在鉴别器线性范围内，其输出误差信号与时延跟踪误差ε的关系为

e(ti,ε)=k2A2(N/D)2D(ε)+ne(ti)=2k2A2(N/D)2ε+ne(ti)。

(15)

由式(15)可知，该鉴别器增益为

kd=2k2A2(N/D)2。

环路鉴别器输出的误差信号e(ti)经过环路滤波器后可得到控制电压信号v(ti)，设环路滤波器的传递函数为H(f)，冲激函数为h(t)，则环路滤波器的输出为[13]

(16)

控制电压信号v(ti)通过控制压控振荡器输出(信号产生时钟)来调整本地信号脉冲相位。压控振荡器的输出信号相位与v(ti)的关系为

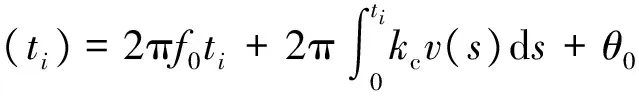
(17)

式中:f0为VCO输出中心频率;kc为VCO增益；θ0是初始相位，可设为0。

压控振荡器根据控制电压信号v(ti)对本地信号相位进行调整更新，更新时间间隔为1个伪码时间周期NcT。环路利用更新的本地信号再次与接收信号进行相关运算和积分清洗，形成闭合环路。经过对本地信号脉冲相位的不断调整，最终锁定接收信号时延，产生稳定的同步输出。

4 跟踪精度分析

进入环路的热噪声是产生时延跟踪误差的主要来源，下面详细分析延迟锁定环路的跟踪精度与热噪声的关系。

由式(3)～(10)可得，I、Q路接收信号与超前、滞后两支路信号进行相关运算和积分清洗结果中的噪声项分别为

(18)

(19)

(20)

(21)

经分析可知，4路积分项nIE(ti)、nQE(ti)、nIL(ti)、nQL(ti)仍为高斯噪声[13]，它们互相独立，均值仍为0，自相关函数均相等，记为Rn(τ)。经过累加后，4路积分项的功率为原来的(N/D)倍，而采样率(带宽)为原来的1/N，故其功率谱密度为(N2/D)·N0/2。则鉴别器输出的噪声项为

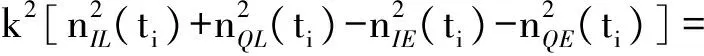
(22)

为了求得最终的时延跟踪误差抖动，需要得到噪声项ne(ti)的功率谱密度，而信号功率谱密度函数为其自相关函数的傅里叶变换。ne(ti)的自相关函数为

Rne(τ)=E[ne(ti)·ne(ti+τ)]= E[ne1(ti)·ne1(ti+τ)]+ E[ne1(ti)·ne2(ti+τ)]+ E[ne2(ti)·ne1(ti+τ)]+ E[ne2(ti)·ne2(ti+τ)]。

(23)

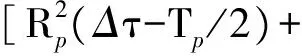
(24)

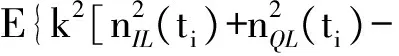
(25)

而由于ne1(ti)的均值为0，则

E[ne1(ti)·ne2(ti+τ)]=E[ne2(ti)·ne1(ti+τ)]=0。

(26)

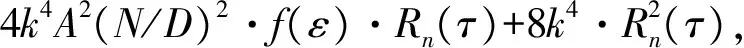
(27)

其功率谱密度为

Sne(f)=4k4A2(N/D)2f(ε)·Sn(f)+ 8k4·[Sn(f)*Sn(f)]。

(28)

对于4路噪声积分项nIE(ti)、nQE(ti)、nIL(ti)、nQL(ti)，其功率谱密度均为

(29)

则有

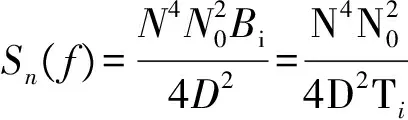
(30)

式中:Bi为相关积分等效带宽，Ti为积分时间。

则当f=0时，有

(31)

而经计算，f(ε)的表达式为

(32)

(33)

式中:kd=2k2A2(N/D)2为鉴别器增益，BL为环路带宽，C/N0=A2/N0为载噪比，Ti为积分时间。σtDLL表示相对跟踪误差，其单位为脉冲宽度Tp。

由此可得到热噪声引起的时延跟踪随机误差为

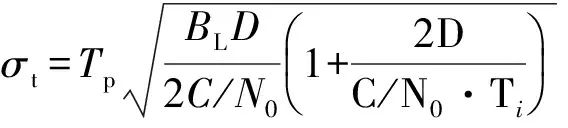
(34)

由式(34)可得到如下结论：

(1)接收信号载噪比C/N0越大，其时延跟踪误差越小。与直扩信号相比，由于脉冲超宽带测控信号由一系列窄脉冲组成，存在一定的占空比，故采用延迟锁定环路对其进行精密跟踪的相对跟踪误差要更大。但由于其脉冲宽度很窄，故其仍可达到很高的时延跟踪精度。

(2)延迟锁定环路的跟踪误差与环路带宽BL的平方根成正比，BL越大，其时延跟踪误差越大。故可通过减小BL来减小时延跟踪误差，但这同时会降低系统的动态适应能力。

(3)相关积分时间Ti越长，其时延跟踪误差越小。故可通过增大相关积分时间来减小环路的时延跟踪误差，但考虑到系统实时性和动态适应性等问题，Ti也不能过长。

(4)脉冲占空比倒数D越大，其时延跟踪误差越大。而若脉冲宽度不变，D越小，则相应的伪码速率越大，会增大信号产生和调制的难度,同时还会减小信号的扩频处理增益，从而降低信号的抗干扰能力。故需综合考虑，对脉冲占空比倒数D进行合理取值。

5 仿真验证

本节对基于延迟锁定环路的脉冲超宽带测控信号时延跟踪方法进行仿真验证。时延跟踪精度决定了系统最终的测距精度，这里主要考虑热噪声带来的跟踪误差抖动，则脉冲超宽带测控系统和直扩测控系统的测距精度表达式分别为[15-16]

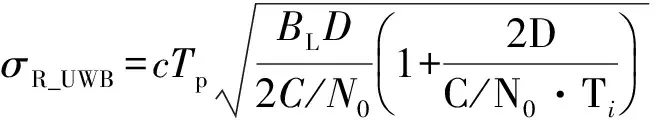
(35)

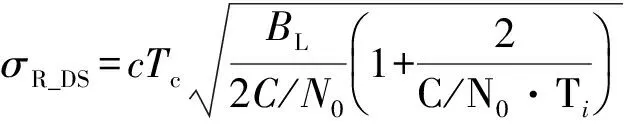
(36)

根据仿真结果可得到两者的相对跟踪误差，再由以上两式可得到对应的测距误差，并进行对比。

5.1 环路可行性验证

首先对延迟锁定环路用于脉冲超宽带测控信号时延精密跟踪的可行性进行仿真验证。脉冲超宽带测控信号参数设置如下：脉冲宽度Tp=1.955 ns，伪码码长Nc=1 023，码速率Rc=102.3 Mchip/s，数据速率Rb=100 kbit/s，中频载波频率fc=511.5 MHz，载噪比C/N0=54 dBHz。假设信号捕获已完成，残余时延同步误差Δτ=-0.2Tp。采用二阶延迟锁定环，环路参数设置如下：阻尼系数ξ=0.707，环路带宽BL=20 Hz，积分时间0.5 ms。则其时延跟踪结果如图3所示。

(a)鉴别器输出

(b)环路跟踪输出

同时对直扩测控信号进行时延跟踪仿真，直扩测控信号的参数设置如下：伪码码长Nc=1 023，码速率Rc=10.23 Mchip/s，数据速率Rb=10 kbit/s，中频载波频率fc=70 MHz，载噪比C/N0=54 dBHz，残余时延同步误差Δτ=-0.2Tc，而环路参数设置保持不变，积分时间同样为0.5 ms。则其时延跟踪结果如图4所示。

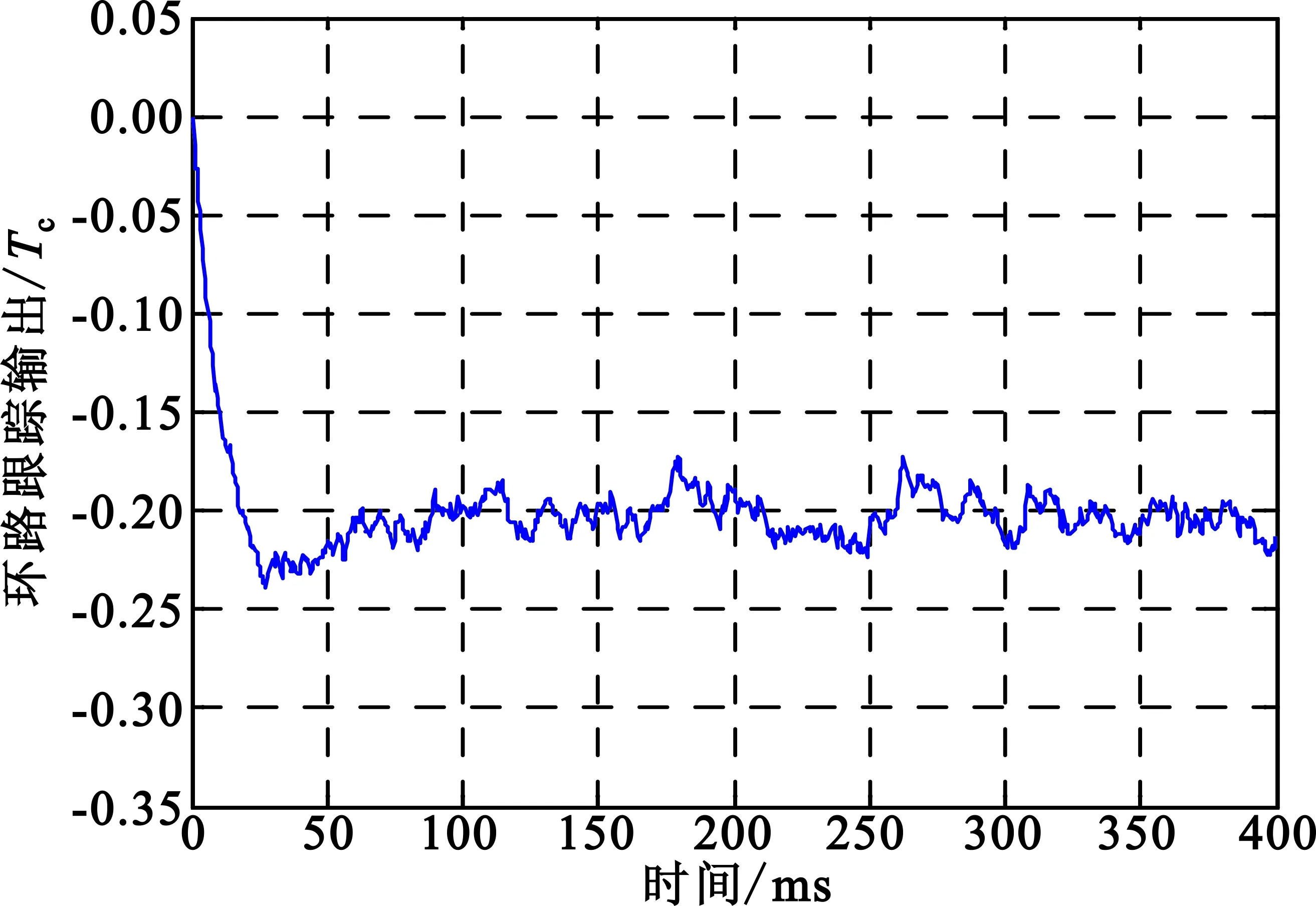
(b)环路跟踪输出

对比图3和图4可知，由于环路带宽相同，两个环路的入锁时间基本相同，而脉冲超宽带信号的时延跟踪误差抖动明显更大，两者的均方根误差分别为0.024 5Tp和0.010 3Tc。可见，采用延迟锁定环路可以完成对脉冲超宽带测控信号的时延精密跟踪，但其相对跟踪误差比现行直扩测控系统更大。然而，由于采用的脉冲宽度很窄(达ns量级)，其实际的测距精度仍明显比直扩测控系统要高。根据式(35)和式(36)，本次仿真中，脉冲超宽带测控信号的测距误差对应为1.44 cm，而直扩测控信号的测距误差为30.21 cm。可见，脉冲超宽带测控系统可大大提高测控系统的测距精度。

下面分别将脉冲超宽带测控接收信号改为相位阶跃信号和相位斜升信号，再次对环路进行仿真。相位阶跃信号设置为在t=200 ms时刻额外产生Δτ′=-0.1Tp的脉冲相位阶跃；而相位斜升信号设置为载波多普勒频率fd=1 kHz，其对应的脉冲相位多普勒频率(相位斜升斜率)为fdc=RcD·fd/fc=18.26 Hz。载噪比C/N0=64 dBHz，其他信号参数和环路参数均保持不变。则对上述两信号的环路跟踪结果分别如图5和图6所示。

(a)鉴别器输出

(b)环路跟踪输出

(a)鉴别器输出

(b)环路跟踪输出

由图5和图6可见，该延迟锁定环路可完成对发生相位阶跃和相位斜升的脉冲超宽带测控信号进行时延精密跟踪，具有良好的动态适应能力，可用于动态环境下脉冲超宽带测控系统的高精度测距。

5.2 环路跟踪精度分析

下面对延迟锁定环路的时延跟踪精度进行仿真分析，主要针对载噪比C/N0、环路带宽BL和积分时间Ti等参数对跟踪精度的影响进行分析。

脉冲超宽带测控接收信号的参数设置、环路参数设置和相关积分时间均与上一节相同。分别改变载噪比C/N0、环路带宽BL和积分时间Ti的取值，可得到时延跟踪精度随各参数变化的关系如图7～9所示。可知，延迟锁定环路的时延跟踪误差随载噪比的增大而减小。当载噪比为58 dBHz以上时，环路跟踪误差可达0.01Tp以下，对应的测距精度达0.6 cm以上。在相同条件下，环路的时延跟踪误差随环路带宽的增大而增大。通过减小环路带宽可降低跟踪误差抖动，提高测量精度。环路带宽的选取需在跟踪精度和动态性能之间进行折中。而环路的时延跟踪误差还随积分时间的增大而减小,但当积分时间达到一定长度后，环路跟踪误差的减小量不再明显。

图7 时延跟踪误差与载噪比的关系

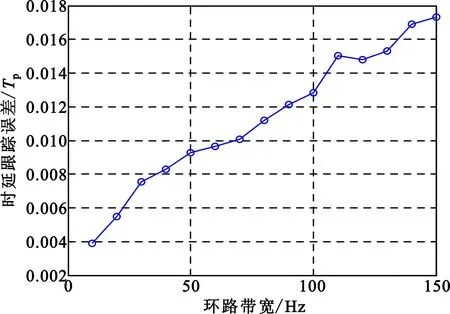
图8 时延跟踪误差与环路带宽的关系

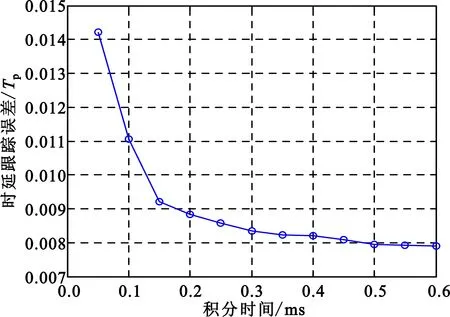
图9 时延跟踪误差与积分时间的关系

6 结 论

本文针对脉冲超宽带测控新体制中的信号时延精密跟踪问题进行了研究。鉴于脉冲超宽带测控信号与直扩测控信号的相似性，在原有伪码跟踪环路的基础上，提出采用延迟锁定环路对脉冲相位进行精细同步。建立了环路数学模型，并对环路跟踪精度进行了理论推导，最后进行了仿真验证。仿真结果表明，本文提出的基于延迟锁定环路的时延跟踪方法可完成对脉冲超宽带测控信号脉冲相位的精密跟踪，从而实现高精度测距。在足够的载噪比条件下，其测距精度可达厘米量级甚至更高。

[1] 廉昕,王元钦,侯孝民,等. 脉冲超宽带技术在航天测控系统中的应用[J].电讯技术,2016,56(9):1005-1010. LIAN Xin,WANG Yuanqin,HOU Xiaomin,et al.Application of impulse radio UWB technology in TT&C system[J].Telecommunication Engineering,2016,56(9):1005-1010.(in Chinese)

[2] 廉昕,王元钦,侯孝民,等. 脉冲超宽带测控体制研究[J].航天控制,2016,34(5):81-85. LIAN Xin,WANG Yuanqin,HOU Xiaomin,et al.Research on impulse radio UWB TT&C system[J].Aerospace Control,2016,34(5):81-85.(in Chinese)

[3] 张欣宇. 脉冲超宽带同步技术的研究[D].哈尔滨:哈尔滨工业大学,2008. ZHANG Xinyu. Research on impulse UWB synchronization techniques[D].Harbin:Harbin Institute of Technology,2008.(in Chinese)

[4] AEDUDODLA S R,VIJAYAKUMARAN S,WONG T F. Timing acquisition in ultra-wideband communication systems[J].IEEE Transactions on Vehicular Technology,2005,54(5):1570-1583.

[5] WON S H,HANZO L. Initial synchronisation of wideband and UWB direct sequence systems:single- and multiple-antenna aided solutions[J].IEEE Communications Surveys & Tutorials,2012,14(1):87-108.

[6] SUN K. Adaptive code tracking loop design for GNSS receivers[C]//Proceedings of 2012 IEEE/ION Position Location and Navigation Symposium(PLANS).Myrtle Beach,South Carolina:IEEE,2012:282-290.

[7] LIU L,AMIN M G. Performance analysis of GPS receivers in non-Gaussian noise incorporating precorrelation filter and sampling rate[J].IEEE Transactions on Signal Processing,2008,56(3):990-1004.

[8] LIU X,LIU J,HONG Z. Code and carrier phase multipath effects with GNSS receiver[C]//Proceedings of 2006 SPIE.Wuhan:SPIE,2006:1-10.

[9] QU B,WEI J,TANG Z,et al.Analysis of combined effects of multipath and CW interference on coherent delay lock loop[J].Wireless Personal Communications,2014,77(3):2213-2233.

[10] JONG Y G,KIM J S,KIM M J. Implementation of code tracking loop for PCS system[C]//Proceedings of 1996 IEEE Asia Pacific Conference on Circuits and Systems.Seoul,Korea:IEEE,1996:49-52.

[11] 朱雯. 直扩MSK信号的快速捕获与跟踪技术研究[D].南京:南京理工大学,2014. ZHU Wen. Research on fast acquisition and tracking techniques of direct sequence spread spectrum MSK signal[D].Nanjing:Nanjing University of Science and Technology,2014.(in Chinese)

[12] 王建平. GNSS接收机跟踪环路的设计与实现[D].北京:北京邮电大学,2010. WANG Jianping. Design and realization of tracking loop in GPS receiver[D].Beijing:Beijing University of Posts and Telecommunications,2010.(in Chinese)

[13] 田日才,迟永钢. 扩频通信[M].2版. 北京：清华大学出版社,2014:244-263.

[14] TANG Z,HU X,HUANG X,et al.A novel analysis on code tracking performance of navigation receivers[C]//Proceedings of Second International Conference on Space Information Technology.Wuhan:SPIE,2007:67953M-1-67953M-6.

[15] WANG P,WANG Y,WU S. A modified code tracking loop based on dual structure[J].Science China Information Sciences,2015,58(8):1-10.

[16] GARRISON J L,LIANG L. Numerical simulation of GNSS code tracking loops using Euler-Maruyama method[J].Electronics Letters,2005,41(15):868-869.

A Timing Tracking Method for Impulse Radio UWB TT&C Signal

LIAN Xin,WANG Yuanqin,HOU Xiaomin,MENG Xiangli

(Department of Photoelectric Equipment,The Academy of Equipment,Beijing 101416,China)

The new impulse radio ultra-wideband(IR-UWB) tracking,telemetry and command(TT&C) system can effectively improve the security performance of the TT&C system,and has a potential high-precision range measuring capability. In order to realize the high-precision range measuring function,a precision timing tracking method based on delay-locked loop for IR-UWB TT&C signal is proposed. This method is improved on the basis of the traditional pseudo-code tracking loop and uses a non-linear feedback loop based on non-coherent integration to track the pulse phase of the received signal. Theoretical analysis and simulation results show that the delay-locked loop in this paper can complete the precision tracking of the IR-UWB TT&C signal. Compared with the direct sequence spread spectrum(DSSS) TT&C signal,the relative timing tracking error of IR-UWB TT&C signal is larger under the same conditions,but because of the quite narrow pulse width,its measuring precision can still reach centimeter level and even higher under certain carrier-to-noise ratio.

impulse radio UWB;TT&C;timing tracking;delay-locked loop;high-precision range measurement

10.3969/j.issn.1001-893x.2017.06.004

廉昕，王元钦，侯孝民，等.脉冲超宽带测控信号时延精密跟踪方法[J].电讯技术，2017,57(6):635-642.[LIAN Xin,WANG Yuanqin,HOU Xiaomin,et al.A timing tracking method for impulse radio UWB TT&C signal[J].Telecommunication Engineering,2017,57(6):635-642.]

2017-01-04；

2017-03-07 Received date:2017-01-04；Revised date：2017-03-07

TN914.2

A

1001-893X(2017)06-0635-08

廉 昕(1987—)，男，吉林长春人，2012年获硕士学位，现为博士研究生，主要研究方向为航天测控系统、脉冲超宽带技术、高速数字信号处理;

Email:lianxin20032002@aliyun.com

王元钦(1963—)，男，黑龙江牡丹江人，2012年获博士学位，现为教授、博士生导师,主要研究方向为航天测控系统、数字信号处理;

侯孝民(1968—)，男，陕西韩城人，2006年获博士学位，现为教授、博士生导师,主要研究方向为航天测控系统、数字信号处理;

孟祥利(1991—)，男，山东潍坊人，2014年获学士学位，现为硕士研究生,主要研究方向为航天测控系统、脉冲超宽带技术。

**通信作者： lianxin20032002@aliyun.com Corresponding author： lianxin20032002@aliyun.com，王元钦，侯孝民，孟祥利