简支钢梁自振频率对预应力敏感性试验研究

丁红岩， 赵思思， 刘 鹏， 郭耀华

(1.天津大学 水利工程仿真与安全国家重点实验室，天津 300072；2.滨海土木工程结构与安全教育部重点实验室(天津大学)，天津 300072；3.天津大学 建筑工程学院，天津 300072)

简支钢梁自振频率对预应力敏感性试验研究

丁红岩1,2,3， 赵思思3， 刘 鹏3， 郭耀华3

(1.天津大学 水利工程仿真与安全国家重点实验室，天津 300072；2.滨海土木工程结构与安全教育部重点实验室(天津大学)，天津 300072；3.天津大学 建筑工程学院，天津 300072)

为了研究简支钢梁基频与预应力值之间的关系，基于FFT(Fast Fourier Transformation，即快速傅氏变换)和HHT(Hilbert-Huang Transform，即希尔伯特黄变换)两种分析方法，以预应力简支钢梁为研究对象，通过不同预应力值下钢梁基频试验研究，对比了两种分析方法的适用性。研究结果表明：传统的力学理论不能很好的解释预应力梁基频与预应力值之间的关系，相比于FFT分析方法，HHT方法能够更好的捕捉到梁体的瞬时频率，梁体基频会随着预应力值的增大而呈现增长的趋势，瞬时频率的震荡幅度也会随之增大。

预应力；简支梁；固有频率；试验研究

0 引言

随着对大跨度空间结构的需求越来越多，预应力技术得到了广泛的应用，尤其在桥梁中的使用更为普遍。对于预应力桥梁，预应力体系承受了桥梁所承受的大部分荷载，其实际受力状况从很大程度上决定了桥梁的健康状况，因此需要对桥梁的预应力体系进行定期的检测。但是在桥梁的运营期间，通过常规手段检测预应力体系的预应力值是较为困难的[1-3]。

桥梁内的预应力体系在张拉完毕后，会对梁体的抗弯刚度等有很大的提高，从而使得桥梁的固有频率发生变化，因此可以对桥梁的固有频率进行检测，进而识别预应力值。在桥梁的长期运营中，混凝土的收缩和超载车辆的通过等都可能使预应力值发生变化，甚至使桥梁出现局部损伤[4-5]。许多文献指出随着预应力值的增大，桥梁的固有频率会随之增大，这与传统的力学理论恰恰相反[6]。基于此实验现象，许多学者提出了新的理论和方法来解释此问题。Saiidi和张耀庭等人[7-9]均基于大量的试验数据，提出了各自的刚度修正公式和预应力梁的频率计算公式。

对于桥梁时域信号处理方法用的最为广泛的是FFT方法，此方法通过离散傅里叶算法，可将时域信号转为频域信号，从而得到梁体的基频信息，但是此方法无法得到梁体在采集时间段内的瞬时频率。梁体在预应力钢绞线轴向力作用下的自振频率通常为一个时变量，只有对其瞬时频率分析才有意义，而HHT是一种相对新颖的非线性非稳态信号处理方法，他从原始信号的特征出发，用EMD(Empirical mode decomposition，即经验模态分解)方法将原始信号分解为一系列的IMF(Intrinsic mode function，本征模态函数)分量，然后对各IMF分量进行Hilbert变换，得到时频平面上能量分布的Hilbert谱图，从而突破了测不准原理的限制，可以更为精确地将信号在时频面上的信息表达出来。

本文在对实测数据进行分析时发现，由于FFT方法不能获得结构的瞬时频率，从而无法得到预应力值与固有频率的关系，因此采用了HHT的方法处理数据。本文以偏心曲线布筋的钢梁为研究对象，采用动态检测的方法进行预应力简支梁的动力试验，研究预应力值与简支梁固有频率的关系，以期为实际工程中预应力值的检测提供理论指导。

1 简支梁动力试验

1.1 试验模型

本次试验用简支梁采用10号工字钢(Q235)进行模拟，并在钢梁腹部设置竖向加劲肋，钢梁总长度为5.2 m，净跨度为4.8 m，试验模型如图1所示。钢梁弹性模量为2.1×105MPa。简支梁一端为固定支座，通过将滚轴焊接在钢板上并用4个螺纹杆将主梁固定来实现；另一端为滑动支座，依靠4个螺纹杆将钢板、滚轴与主梁固定；2个支座底部通过膨胀螺栓固定在地面上，支座形式如图2所示。

图1 钢梁总体布置图(单位：mm)

1.2 预应力施加方式

梁体中的预应力钢绞线通过两根直径2 mm的7×7-304#不锈钢丝绳进行模拟，钢丝绳通过相应的螺栓卡扣固定于梁体梁端，试验中可通过调整梁体两端的螺栓，来实现对钢丝绳拉力大小的调整。钢绞线穿过梁体竖向加劲肋中的孔洞，且中间与钢梁没有固定，在张拉状态下与钢梁无接触。预应力值通过拉力传感器进行测试，拉力传感器通过带滚轴的吊环与钢丝绳串联连接，钢丝绳、拉力传感器及预应力调控装置如图3所示。

1.3 试验方案

此次试验主要是为了研究预应力简支梁中预应力与梁体固有频率之间的关系，基于上述试验模型，采用偏心的方式布置预应力钢丝绳。加载时，对钢丝绳分别的张拉0 N、100 N、200 N和300 N的张拉力，用以模拟不同的预应力值。在每级荷载加载完毕后，采用锤击法在钢梁1/6处进行激励，由布设于梁体上的加速度传感器采集梁体振动信号，试验过程中的现场照片如图3所示。

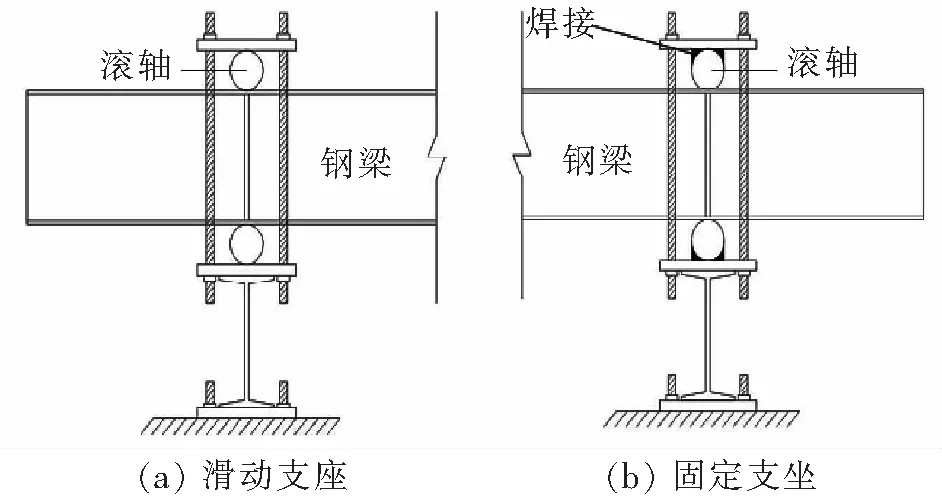
图2 支座形式

图3 现场测试照片

2 理论分析方法

基于传统力学理论，将梁体视为各向同性的材料，可以得到简支梁在梁两端受压状态下的固有频率ωn，计算公式为[10-11]

(1)

式中，n为正整数；l为梁体的净跨；N为梁体两端所受的轴向压力；EbIb为梁体的抗弯刚度；ρA为梁体的分部质量。

传统的力学理论认为，物体在压力作用下，其自振频率会降低，在拉力作用下，其自振频率会增大。因此，从公式(1)中可以看出，简支梁的自振频率会随着梁体两端预应力的增大而减小，但是从目前既有的试验结果来看，预应力梁中的预应力与梁体自振频率的关系完全相反。基于此试验现象，有必要寻求新的途径来解决此问题，许多学者提出了新的理论和方法来解释此问题。Saiidi和张耀庭等人均基于大量的试验数据，提出了各自的刚度修正公式和预应力梁的频率计算公式。

目前常用的预应力梁基频分析方法有基于FFT的实测数据分析法和有限元分析法等，由于钢梁在施加预应力后，其整体的振动成为一个时变系统的振动，用常规的频域分析方法很难得到其频率的变化[12]。基于有限元线弹性的动力分析中，一般均把预应力当做外荷载施加于梁体两端，并不改变梁体本身的刚度矩阵和质量矩阵，因此并不能区分出预应力大小与梁体基频之间的关系。

为了很好的区分预应力梁体中预应力与自振频率之间的关系，此处引入了一种新的瞬时频率分析方法，即Hilbert-Huang Transform变换方法，简称为HHT方法。此方法第一步先基于EMD把原始信号分解为若干个IMF分量；第二步再对每个IMF进行HHT变换，即可得到信号的Hibert谱，此Hibert谱可描述结构的频率随时间的变化及分布情况，也即梁体的瞬时频率。对于简支梁，消除梁体两端的端点效应后，对梁体瞬时频率进行线性拟合后，可得到梁体的1阶频率。

3 试验结果分析

按照试验方案，对梁体钢丝绳施加不同的预应力后，采集钢梁受锤击作用下的加速度信号，然后对所采集的信号进行滤波处理，最后分别基于FFT和HHT方法对数据进行分析。

3.1 基于FFT的基频分析

基于通用的FFT分析方法，对所采集到的梁体加速度信号进行分析，可以得到梁体在不同预应力下的频谱曲线，如图4所示。

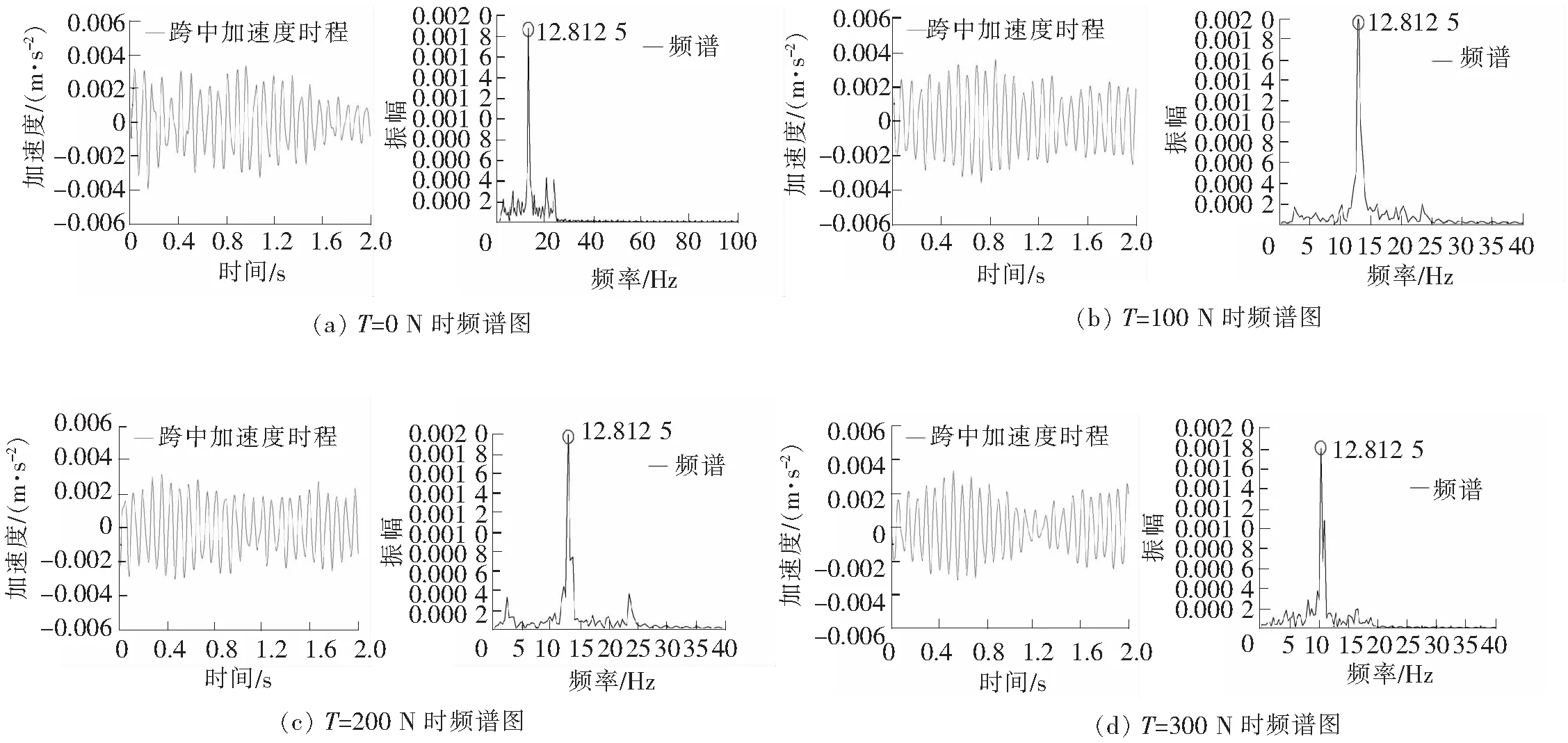
图4 基于FFT的梁体频谱曲线

从图4中可以看出，基于FFT分析方法对不同预应力状态下钢梁自振频率的分析结果没有变化，均为12.812 5 Hz，也即FFT分析方法对预应力梁体中的预应力值并不敏感，基于此方法无法得到梁体内预应力大小与基频之间的关系，因此需要寻找别的方法来进行更为深入的分析。

3.2 基于HHT的基频分析

采用Matlab软件对HHT分析方法进行编程，对于同样的钢梁加速度信号，此处基于HHT分析方法进行重新的分析，可以得到各工况下的钢梁自振频率。此处以T=300 N预应力工况为例，对基于HHT的数据分析流程进行说明。

在对原始信号进行滤波后，基于EMD把原始信号分解为若干个IMF分量，此处列出前4个IMF分量，如图5所示。 对第一个IMF分量进行HHT变换，可以得到其瞬时频率和相位角，其中相位角对试件求导可以得到梁体在振动过程中的瞬时频率，梁体在T=300 N工况下的瞬时频率如图6所示，其相位角如图7所示。

图5 IMF分量

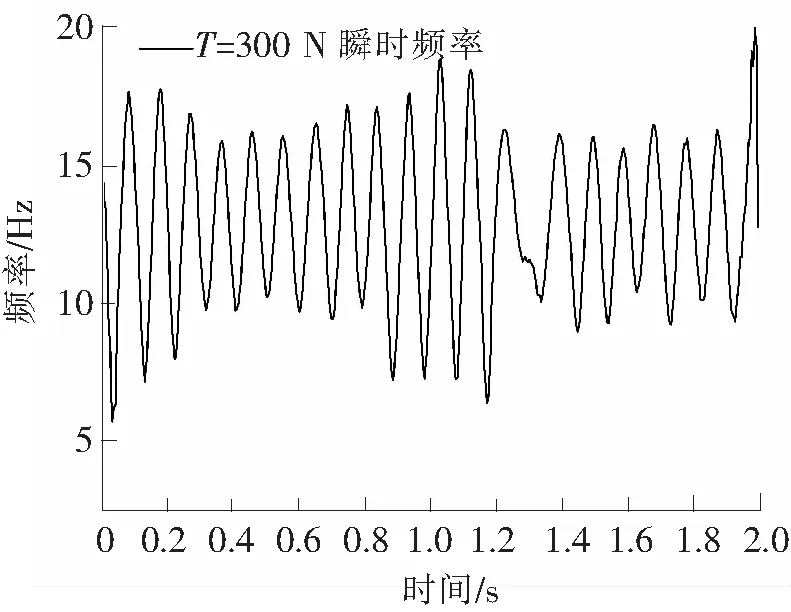
图6 瞬时频率

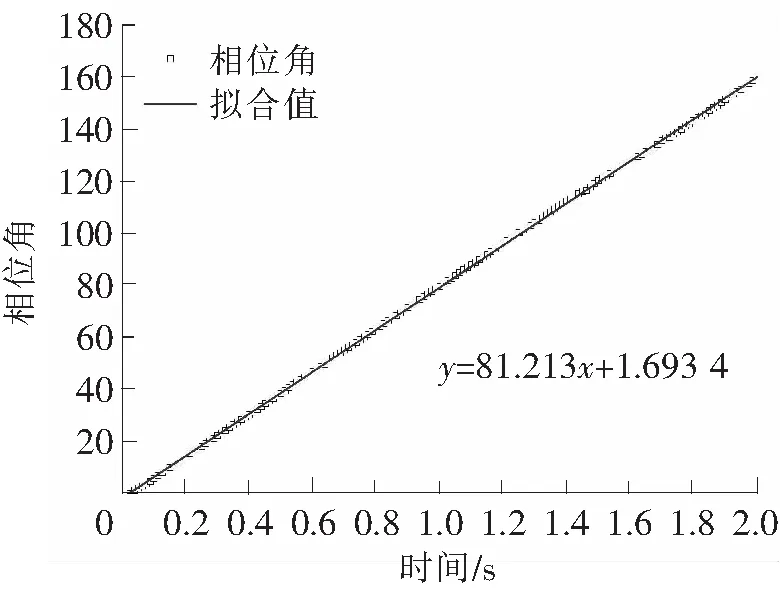
图7 相位角拟合

从图7中可以看出，IMF1的相位角具有较好的线性关系，与拟合的线性方程较为吻合，则此时梁体的基频为

(2)

基于同样的方法和程序，可以得到梁体在0 N、100 N、200 N和300 N预应力值下的基频分别为12.870 9 Hz、12.899 7 Hz、12.920 5 Hz和12.925 5 Hz。

3.3 试验结果对比分析

对基于FFT和HHT两种分析方法所得到的预应力梁基频结果进行汇总，如图8所示。从图8中可以看出，FFT方法基本无法分析出预应力值大小对梁体基频的改变，在几种不同预应力值作用下，梁体的基频分析结果均未发生变化；基于HHT分析方法的分析结果显示，梁体基频随着预应力值的增大而逐渐的增大，但也不是呈现完全的线性增长；在无预应力状态下，两种分析方法的基频误差为0.468%，说明分析结果具有较强的可信性。

HHT分析方法一个很大的特点就是可以得到结构的瞬时频率，也即频率与时间的关系，在分析完预应力与基频之间的关系后，为了更加深入的了解预应力与瞬时频率之间的关系，此处取T=0 N和T=300 N两种工况的瞬时频率谱进行对比分析，如图9所示。从图9中可以看出，梁体预应力值的增大，会使得梁体频率的变化幅度增大。

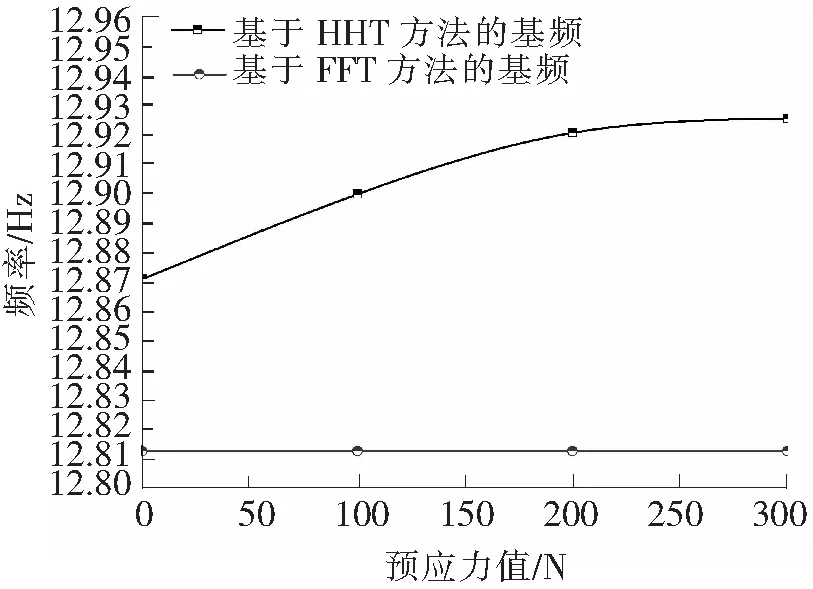
图8 不同分析方法的基频

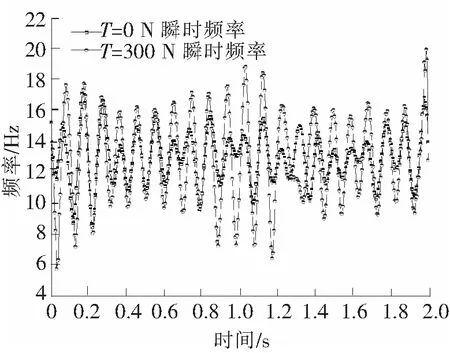
图9 不同工况下瞬时频率-时间谱

从上述分析结果可以看出，简支梁自振频率在一段时间内是一个变量，基于常规的FFT分析方法很难得到预应力与频率之间的关系，这也是之前的一些研究中无法准确得到准确结论的一个重要原因，采用HHT分析方法则可很好的解决此问题。

4 结论

本文通过预应力钢梁模型试验，研究了简支梁基频与预应力值之间的关系，从不同频谱分析方法的分析结果可以得到以下主要结论：

(1)传统的力学理论不能很好的解释预应力梁基频与预应力值之间的关系，其理论值与实测值正好相反。

(2)FFT分析方法不能获得结构的瞬时频率，也无法得到基频随预应力值的变化情况。

(3)基于HHT的频谱分析方法能够很好的捕捉到梁体的瞬时频率，且分析结果对预应力值较为敏感，能够真实的反映出梁体频率与预应力值之间的关系。

(4)梁体基频会随着预应力值的增大而呈现增长的趋势，瞬时频率的震荡幅度也会随之增大。

[1]Bruno Godart. Pathology, appraisal, repair and management of old prestressed concrete beam and slab bridges [J]. Structure and Infrastructure Engineering，2015, 11 (4):501-518．

[2]黄颖,房贞政.预应力混凝土简支梁静力及动力性能有限元分析研究[J]. 武汉理工大学学报：交通科学与工程版,2013,37(1):123-126.

[3]李士元. 客运专线32 m双线整孔简支箱梁张拉应力试验研究[J]. 石家庄铁道大学学报：自然科学版, 2014,27(1):24-30.

[4]Classen Martin,Dressen Tobias.Experimental Investigations on Prestressed Concrete Beams with Openings[J]. ACI Structural Journal,2015, 112 (2):221-232.

[5]王勇. 既有大准铁路16 m简支T梁横向加固研究及应用[J]. 石家庄铁道大学学报：自然科学版, 2015,28(1):54-57.

[6]Luning Shi, Haoxiang He, Weiming Yan, et al. Prestress Force Identification for Externally Prestressed Concrete Beam Based on Frequency Equation and Measured Frequencies[J]. Structural and Mechanics, 2014(2):1-13.

[7]Saiidi,Douglas M, Feng B. Prestress force effect on vibration frequency of concrete bridges [J]. Mathematical Problems in Engineering, 1994, 120(7): 2233-2241.

[8]张耀庭,汪霞利,李瑞鸽.全预应力梁振动频率的理论分析与试验研究[J]. 工程力学,2007, 24 (8):116-120．[9]何涛,张巍,吴植安.基于动静载试验数据的预应力混凝土梁模型修正方法试验研究[J]. 公路交通科技,2015,32(12) :75-80．

[10]张耀庭，李宏健. 全预应力砼梁动力性能试验研究[J]. 工程力学，2008,25( S1):71-75．

[11]王慧东, 马其森. 韩江大桥(48+80+80+88+48)m道岔连续梁车桥耦合动力响应分析[J]. 石家庄铁道大学学报：自然科学版, 2015,28(1):12-16.

[12] 刘寒冰,王龙林,谭国金,等. 预应力对体外预应力简支钢梁自振频率的影响[J]. 吉林大学学报：工学版，2013,43(1):37-39.

Experimental Study on Sensitivity of Steel Beam InherentFrequency to Impact of Prestress

Ding Hongyan1,2,3， Zhao Sisi3， Liu Peng3， Guo Yaohua3

(1.State Key Laboratory of Hydraulic Engineering Simulation and Safety, Tianjin University, Tianjin 300072, China;2.Key Laboratory of Coast Civil Structure Safety (Tianjin University), Ministry of Education, Tianjin 300072, China;3.School of Civil Engineering, Tianjin University, Tianjin 300072, China)

In order to study the relationship between the fundamental frequency of simple steel beam and prestressed value, two analysis methods based on FFT(Fast Fourier Transformation) and HHT(Hilbert-Huang Transform), with prestressed simply-supported steel beam as the research object, by the research on the steel beam under different prestress value base frequency, the applicability of the two analysis methods are compared. The results show that the traditional mechanics theory cannot well explain the relationship between the fundamental frequency and prestress value, compared with FFT analysis method. The HHT method can better capture the instantaneous frequency of the beam body. The fundamental frequency will increase with the increase of prestress value, and the instantaneous frequency of the oscillation amplitude will increase too.

prestress; simply supported beam; fundamental frequency; experimental study

国家自然科学基金(51379142)

丁红岩(1963-)，男，教授，博士，博导，从事土木及海洋工程结构研究。E-mail: dhy_td@163.com

TU317；TU378.2

A

2095-0373(2017)02-0001-06

2016-03-01 责任编辑:刘宪福

10.13319/j.cnki.sjztddxxbzrb.2017.02.01

丁红岩，赵思思，刘鹏，等.简支钢梁自振频率对预应力敏感性试验研究[J].石家庄铁道大学学报:自然科学版,2017,30(2):1-5,36.