基于多小波包排列熵和流形学习的故障特征提取方法
邓飞跃, 唐贵基
(1.石家庄铁道大学 机械工程学院,河北 石家庄 050043;2.华北电力大学 能源动力与机械工程学院,河北 保定 071003)
基于多小波包排列熵和流形学习的故障特征提取方法
邓飞跃1, 唐贵基2
(1.石家庄铁道大学 机械工程学院,河北 石家庄 050043;2.华北电力大学 能源动力与机械工程学院,河北 保定 071003)
针对振动信号非线性、非平稳性导致的故障特征难以准确提取的问题,提出了一种基于多小波包排列熵和流形学习的故障特征提取方法。首先,利用多小波包分解方法得到故障信号的多维多小波系数,通过计算排列熵初步提取了各个小波系数中的故障特征信息;然后利用局部切空间排列(LTSA)流形学习方法对多维特征信息进行处理,在有效降低信息冗余度的同时,提取了其中主要的故障特征;最后利用支持向量机(SVM)对滚动轴承正常、外圈、内圈和滚动体故障实测信号进行故障模式识别试验。结果表明,该方法可以准确地识别出轴承不同的故障类型,并且在提取故障特征准确性方面要优于传统的单小波包方法和主成分分析(PCA)方法。
故障特征;多小波包;排列熵;流形学习;支持向量机
0 引言
在工程实际中,机械故障振动信号大多具有非线性、非平稳的特性[1],采用傅立叶变换方法只能得到信号在频域内的整体分布情况,难以提取到准确的故障特征信息。小波变换具有良好的时频多分辨特性,可以在不同尺度上描述信号的局部特征,但正交小波变换只能对信号低频部分进行分解,无法提取信号高频部分的细节信息。相比而言,小波包变换可以对信号低频和高频部分同时进行精细分解,因此可以根据信号自身特征自适应地选择相应频带进行分析,能更为有效地提取信号的故障特征[2]。
多小波是基于单小波理论的新发展,由多个尺度函数和小波函数构造而成,具有很多优良的特性,克服了单小波无法同时满足紧支性、对称性、正交性及高阶消失矩的问题[3]。多小波包方法是对多小波的进一步扩展,能够对信号进行更加精细地分解和提取。目前,多小波理论已逐步应用于机械故障诊断领域:文献[4]应用多小波分析方法,通过自适应选取阈值实现了滚动轴承故障振动信号的降噪处理;文献[5]根据所分析故障信号的特点,提出了多小波自适应提升构造方法,结合谱峭度理论提取了滚动轴承微弱的故障特征;文献[6]利用多小波相邻系数间的相关性,提出采用平移不变多小波相邻系数方法对齿轮箱微弱故障进行诊断。上述方法都取得了不错的效果,但由于多小波变换后系数的多维性,导致其结果存在较大的冗余信息,分析过程缓慢,处理效率较低。
流形学习可以发现嵌入在高维数据中的非线性结构[7],具有良好的降维效果和数据可视化能力。因此,结合多小波包分解、排列熵和流形学习提出了一种新的故障特征提取方法,利用流形学习降维提取多小波包系数排列熵得到的高维特征信息对滚动轴承进行模式识别,结果表明,相比传统小波包分解方法和主成分分析(PCA)降维方法,该方法具有更好的准确性和可靠性。
1 多小波介绍
1.1 多小波分解
同单小波一样,多小波构造的基本框架也是基于多分辨率分析思想,区别在于它是由有2个或2个以上小波函数经过伸缩平移生成的,因此对应有多个尺度函数。多尺度函数和多小波函数分别表示如下
(1)
两函数满足如下的尺度矩阵方程
(2)
式中,Gk和Hk为r×r的滤波器系数矩阵。目前,应用最为广泛的是r=2的GHM多小波[8],它通过分形插值法构造而成,同时满足紧支性、对称性、正交性和二阶消失矩特性,本文中选择使用GHM多小波,它的滤波器系数矩阵[9]为


多小波分解公式[10]为
(3)
多小波的重构公式为
(4)
式中,Cj-1,k和Dj-1,k分别为r维低频系数和高频系数;“*”表示共轭转置算子。
1.2 多小波包分解
多小波包的构造方式与单小波包相似,令U0(t)=φ(t),U1(t)=φ(t),将尺度子空间Vj和小波子空间Wj统一起来表示为U″j,定义
(5)
则多小波包重构公式为
(6)
本文利用GHM多小波对信号进行3层多小波包分解,分解示意图如图1所示。采用重复采样的预处理方式处理原始信号S0,得到由信号S1和S2组成的2维矩阵。多小波包1层分解后得到信号低频部分为L1和L2,高频部分为H1和H2,同理,3层分解后得到8个频带的2维矩阵信号。相比单小波包分解,多小波包分解可以匹配信号中多种故障特征波形,分解后每个频带信号都是多维矩阵形式,能够提取到更准确、丰富的故障信息。

图1 多小波包3层分解示意图
2 排列熵
排列熵(Permutation Entropy, PE)是由Christoph Bandt[11]提出的一种平均熵参数,用于衡量一维时间序列的复杂程度,与LyaPunov指数、分形维数等复杂度参数相比,它的计算更为简单,抗噪声能力更强。具体算法如下[12]:
设一维序列为{x(i),i=1,2,…,n},对其进行相空间重构,得到矩阵

(7)
式中,m和τ分别为嵌入矩阵的维数和延迟时间;k=n-(m-1)τ。把空间矩阵中每一行看作一个重构分量,将矩阵中第j个分量[x(j)x(j+τ)…x(j+(m-1)τ)]按照升序重新排列,j1,j2,…,jm表示分量中各个元素的排序,那么对于这个空间矩阵可以得到一组符号序列:X(j)=(j1,j2,…,jm),其中,1≤j≤k。m维空间矩阵共有m!=1×2×…×m种可能的符号序列。每一种符号序列出现的概率为p1,p2,…,pk,此时x(i)的排列熵按照Shannon熵形式定义为
(8)
相应的排列熵归一化表示为
(9)
时间序列越规则,Hp越小,反之则越大,通过计算排列熵可以反映并放大序列中极为微弱的特征信息。故障信号经多小波包分解后得到多维信号矩阵,求解矩阵中每个分量的排列熵,可以在简化矩阵分量的同时,准确提取出每个分量中蕴含的故障特征变化信息。
3 局部切空间排列的流形学习方法
局部切空间排列(local tangent space alignment, LTSA)是一种新型的流形学习方法,它的参数鲁棒性和主流形重构有效性要比LE、LIE等方法更明显,因此更适合用于提取非线性机械系统的故障特征信息。LTSA算法通过无限逼近每一样本点的切空间来构造低维流形的局部几何空间,然后观测数据点在空间内投影来获取整体的局部低维坐标。给定一个样本集合y={y1,y2,…,yn},yi∈Rm,LTSA提取一个d(m>d)维主流形的过程如下[13]:
(1)选取样本点领域。基于每个样本点yi,根据选取包括其自身在内的k个最近距离点为邻域构建矩阵Yi=[yi1,yi2,…,yij]。

(10)
(3)整合局部坐标。将每个样本点局部坐标Θi排列得到一个全局坐标T=[τ1,τ2,…τn],其中τi=(τi1,τi2,…,τik),需建立的映射关系要能够极小化重构误差
(11)
式中,Li待定映射矩阵;e为元素为1,长度为k的列向量。
4 多小波包排列熵与流形学习的特征提取方法
利用多小波包同时具有诸多优良特性的性质,对故障振动信号进行多分辨率分析,得到比传统小波包分解后更为精细和准确的多维故障信息矩阵,再结合排列熵算法简化信号多个频带中的故障信息,利用流形学习的非线性信息处理能力进一步提取高维故障信息矩阵的低维特征,在降低故障数据冗余度的同时,有效提取分类准确度高的故障特征。该方法流程如图2所示,具体步骤如下:
(1)对样本信号进行3层GHM多小波包多分辨率分解,得到8个频带16行信号。
(2)分别计算每行信号的排列熵,并将其组成一个16维的特征向量
(12)
(3)目标维数设定为3,利用LTSA流形学习方法对多小波包排列熵组成的特征向量进行低维流形特征提取。
(4)将提取到的流形特征作为特征向量,输入已建立的SVM,完成分类模式识别。
5 试验分析
5.1 试验描述
试验是在QPZZ-Ⅱ滚动轴承试验台上完成的,图3为测试试验平台。测试轴承为洛阳轴承厂生产的型号是6205的深沟球轴承,利用线切割方式在轴承内、外圈和滚动体上加工宽为0.2 mm、深为1.5 mm的沟槽来模拟实际故障工况。加速度传感器位于故障轴承座上方,转轴转速为1 480 r/min,采样频率为12 800 Hz。截取滚动轴承4种工况下信号时域波形如图4所示。

图2 算法流程图

图3 轴承试验台结构

图4 滚动轴承4种工况下时域信号
5.2 试验结果分析
首先在滚动轴承正常、外圈故障、内圈故障和滚动体故障4工况下各选取20个样本信号,每个样本为4 096个数据点,分别对其进行GHM多小波包和“db4”单小波包分解,计算各个小波包系数的排列熵值,其中设置参数m=6、τ=3。图5和图6分别为两种方法下提取每个样本的排列熵均值。从图5中可知,多小波包分解后得到各个工况下样本排列熵均值之间有明显的间隔,分类效果较好;图6单小波包分解后各样本排列熵均值中,只有滚动体故障分离较为明显,其余3种工况虽然也能区分但彼此间隔不大,分类效果较差。
采用LTSA流形学习方法对多小波包分解后各个分量的排列熵进行特征提取,图7为轴承各工况下故障特征提取效果图,领域参数k=8。从图中可以看出,滚动轴承4种工况下各样本的特征基本聚集在一点,4种工况已经完全分开,并且提取的故障特征具有较好的聚类性能。
PCA方法也是较为常用的数据降维和特征提取方法,为更好进行比较,本文采用PCA方法对各个样本多小波包排列熵特征向量进行3维降维提取,图8为PCA特征提取的效果图。相比图7,4种工况下的样本采用PCA方法也基本实现了分离,但由于不同工况下样本故障特征分布较为分散,样本特征聚类性较差,分类识别效果不如LTSA方法。
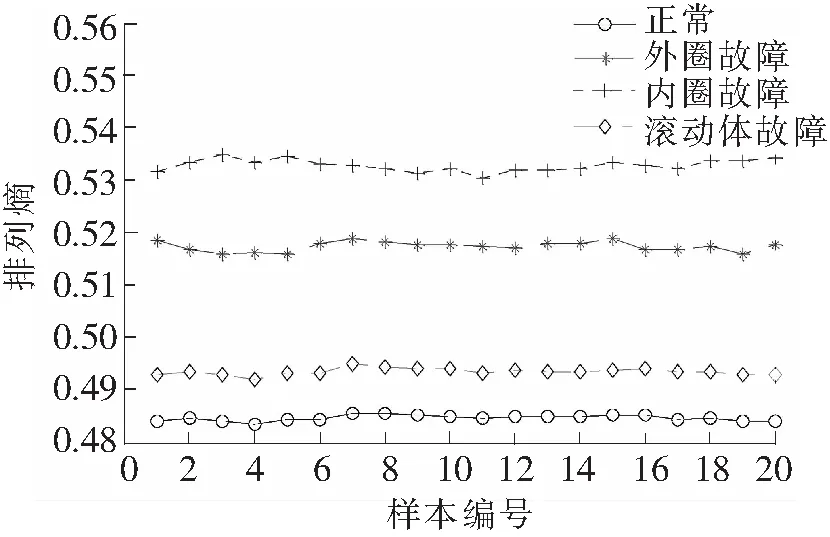
图5 多小波包排列熵样本均值分布
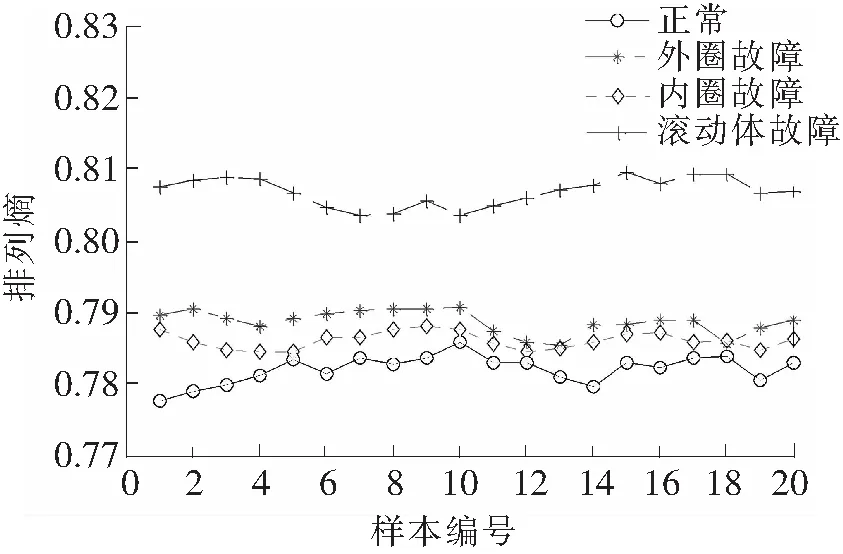
图6 单小波包排列熵样本均值分布
5.3 基于SVM的故障诊断
支持向量机(support vector machine, SVM)具有优秀的小样本学习能力,能较好解决非线性、高维度、局部极小值等问题[14]。因此,建立“一对多”分类模型的SVM用于滚动轴承故障模式的智能识别,核函数采用径向基核函数,参数设置为δ=3,C=150。在滚动轴承4种工况下各采集70个样本数据,数据长度为4 096点,随机在各工况选取20样本中作为测试样本,其余的200个样本用于测试。计算样本的多小波包排列熵(第1阶段),采用LTSA方法提取各个样本的3维特征信息作为特征向量(第2阶段),输入已建立的SVM,识别结果如表1所示。从表中可知,第1阶段所提取故障特征用于分类识别,识别率较低,并且由于此时特征向量维数为12,大大多于LTSA提取后的3维,所以训练和测试时间也更长,因此有必要进行进一步的特征提取。相比单小波包分解和PCA降维方法,所提方法故障模式识别率可以达到100%,这也证明了该方法提取故障特征的准确性和用于故障模式分类的优越性。

图7 LTSA特征提取效果

图8 PCA特征提取效果

标签故障训练样本测试样本第一阶段识别率/%本文方法识别率/%单小波包识别率/%PCA识别率/%1正常 20508010094962外圈故障 20507410094903内圈故障 20508210092844滚动体故障2050821009680
6 结论
基于多小波包、排列熵和LTSA流形学习方法提出了一种新的故障特征提取方法,该方法将多小波包系数排列熵作为特征向量,通过流形学习提取了故障信息的低维特征,有效减少了多小波包分解后冗余信息,简化了故障特征向量。最后通过实验室条件下滚动轴承不同故障模式的试验分析,证实了所提方法准确性,并且其故障特征提取和模式识别的效果要优于单小波包和PCA方法,具有一定的工程应用价值。由于条件所限,未能加工出更为微弱的轴承故障,关于微弱故障特征的提取将是今后需要进一步研究的方向。
[1]侯丽娴,杨绍普,刘永强,等. 基于共振解调的铁路货车轴承故障诊断[J]. 石家庄铁道大学学报:自然科学版, 2013, 26(4):47-51.
[2] 芦吉云, 王帮峰, 梁大开. 基于小波包特征提取及支持向量回归机的光纤布拉格光栅冲击定位系统[J]. 光学精密工程, 2012, 20(4):712-718.
[3] 赵志宏, 杨绍普, 刘永强. 多小波系数特征提取方法在故障诊断中的应用[J]. 振动、测试与诊断, 2015, 35(2):276-280.
[4] Zhao Zhihong, Yang Shaopu, Liu Yongqiang. Application of feature extraction method in fault diagnosis based on multi-wavelet coefficients[J]. Journal of Vibration, Measurement & Diagnosis, 2015, 35(2):276-280.
[5] 张建宇, 李文斌, 张随征,等. 多小波自适应阈值降噪在故障诊断中的应用[J]. 北京工业大学学报, 2013, 39(2):166-173.
[6] 王晓冬, 何正嘉, 訾艳阳. 滚动轴承故障诊断的多小波谱峭度方法[J]. 西安交通大学学报, 2010, 44(3):77-81.
[7] 袁静, 何正嘉, 王晓东,等. 平移不变多小波相邻系数降噪方法及其在监测诊断中的应用[J]. 机械工程学报, 2009, 45(4):155-160.
[8] Wang Yi, Xu Guanghua, Liang Lin, et al. Detection of weak transient signals based on wavelet packet transform and manifold learning for rolling element bearing[J]. Mechanical Systems and Signal Processing, 2015(54/55):259-276.
[9] 孙海亮, 訾艳阳, 何正嘉. 多小波自适应分块阈值降噪及其在轧机齿轮故障诊断中的应用[J]. 振动工程学报, 2013, 26(1):127-134.
[10] 卢娜. 基于多小波的水电机组振动特征提取及故障诊断方法研究[D]. 武汉:武汉大学, 2014.
[11] Sun Hailiang, He Zhengjia, Zi Yanyang, et al. Multiwavelet transform and its applications in mechanical fault diagnosis-A review[J]. Mechanical Systems and Signal Processing, 2014, 43(1-2):1-24.
[12] Bandt C, Pompe B. Permutation entropy: a natural complexity measurefor time series[J]. PhysRevLett,2002,88(17): 21-24.
[13] 冯辅周, 饶国强, 司爱威,等.排列熵算法研究及其在振动信号突变检测中的应用[J]. 振动工程学报, 2012,25(2):221-224.
[14] 顾晓辉,刘永强,杨绍普,等.基于混沌吸引子特征量的滚动轴承故障诊断[J]. 石家庄铁道大学学报:自然科学版, 2015, 28(1):91-95.
Fault Feature Extraction Method Based on Multi-wavelet PacketPermutation Entropy and Manifold Learning
Deng Feiyue1, Tang Guiji2
(1.Department of Mechanical Engineering, Shijiazhuang Tiedao University, Shijiazhuang 050043, China;2.School of Energy, Power and Mechanical Engineering, North China Electric Power University, Baoding 071003, China)
Aiming at the problem that fault feature is difficult to accurately extract because of the nonlinear and non-stationary of vibration signal, a new method based on the multi-wavelet packet permutation entropy and manifold learning theory is presented to extract fault feature. Firstly, multi-dimensional wavelet coefficients of fault signal are obtained by multi-wavelet packet decomposition, and fault feature information of each wavelet coefficient is preliminarily extracted by calculating permutation entropy. Secondly, in order to reduce the information redundancy, but also extract the main fault feature information, multi-dimensional fault features are processed by local tangent space alignment (LTSA). Finally, a support vector machine (SVM) is used to classify different fault patterns of rolling element bearing with normal, outer race fault, inner race fault and rolling body fault. The results indicate the proposed method can accurately identify different fault pattern of bearing, moreover the accuracy of fault feature extraction is superior to the traditional unit-wavelet packet method and principal component analysis (PCA) method.
fault feature;multi-wavelet packet;permutation entropy;manifold learning;SVM
邓飞跃(1985-),男,讲师,主要从事机械设备故障诊断的研究。E-mail: dengfeiy@126.com
TP206
A
2095-0373(2017)02-0046-07
2016-04-20 责任编辑:车轩玉
10.13319/j.cnki.sjztddxxbzrb.2017.02.08
邓飞跃,唐贵基.基于多小波包排列熵和流形学习的故障特征提取方法[J].石家庄铁道大学学报:自然科学版,2017,30(2):46-52.

