考虑流固耦合CFRP拉索风雨激振数值模拟*

杨吉新 黎建华 余 越 孙亭亭 刘 杰

(武汉理工大学交通学院1) 武汉 430063) (中交第二公路勘察设计研究院有限公司2) 武汉 430050)

考虑流固耦合CFRP拉索风雨激振数值模拟*

杨吉新1)黎建华1)余 越2)孙亭亭1)刘 杰1)

(武汉理工大学交通学院1)武汉 430063) (中交第二公路勘察设计研究院有限公司2)武汉 430050)

以肇庆市阅江大桥工程为背景，采用Davenport脉动风速谱，基于自回归模型方法模拟拉索水平脉动风速时程.利用WORKBENCH针对上述计算的风场情况，考虑最易产生风雨激振现象工况，对考虑流固耦合钢索及CFRP拉索风雨激振进行数值模拟.计算结果表明，CFRP索对比传统钢索而言，在风雨激振响应上表现更好，但CFRP索的振动频率更快.

自回归模型；结构风场；流固耦合；CFRP拉索；风雨激振

0 引 言

随着碳纤维复合材料(carbon fiber reinforced polymer/plastic,CFRP)在工程领域的应用研究不断取得进展，将CFRP作为拉索材料应用于斜拉桥中已成为桥梁工程新的发展方向[1-3].相对于传统斜拉桥的钢索材料，CFRP拉索在结构上表现更为轻巧，因此，其对风荷载作用更为敏感.尤其是对于大跨径斜拉桥，由于空间结构更大，其抗风稳定性是结构稳定的主要因素之一[4-5].而风雨激振作为拉索振幅最大、对结构危害最为严重的拉索风致振动，一直是桥梁风振机制研究的重点对象.在CFRP材料发展如此迅猛的今天，研究其作为索结构的风雨激振现象已是丞待解决的问题之一.

Ruscheweyh[6]首次在桥上观测到了在风雨天气下，斜拉索会产生大幅振动现象.Yamaguchi[7]在利用粘贴人工水线的方式，对拉索三分力进行测量计算，并最早对拉索风雨激振的原理进行了理论分析，其通过分析建立的弯扭耦合两自由度模型对后来学者影响较大.

在风雨场中，雨水在拉索上附着，水线会随着拉索的振动沿索表面作环向振荡运动，在这一过程中水线经历着生成、脱落、再生成，由于索截面形状的改变，进而激烈地改变索周围风压，进而又影响到索结构的振动，因此拉索的风雨振是风、雨、索三相耦合的行为.

文中以肇庆市阅江大桥为工程背景，以等效刚度法将钢索替换为CFRP拉索，采用粘贴固定人工水线的方法，对考虑流固耦合的两类材料拉索的风雨激振进行模拟，得到了普通钢索及CFRP拉索在风雨场作用下风压及振动幅度、频率的变化情况，以期探索CFRP拉索相对传统钢索在风致振动上的优缺点，为未来斜拉桥向更大跨径发展提供理论支持.

1 风场模拟

对风荷载作用下的大跨度斜拉桥的斜拉索，拉索空间分布较为分散，而不同高度风速表现行为不一，因而考虑不同高度风场分布，对桥梁所在桥位处进行随机风速场的数值模拟显得很有必要.从各类实测资料及实验中可以发现，瞬时风速由某一时间段的平均风及较短周期的随机脉动风两类组成.

1.1 平均风速

平均风速通常通过两种模型表示，即按实际测量结果拟合的指数律模型和通过边界层理论推导的对数律模型.目前国内外研究中都倾向于采用前者，即

(1)

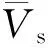
1.2 脉动风速

脉动风速周期一般为几秒，其形成为风受地表环境影响产生了涡流现象，在速度上呈现随机脉动的特点[8].一般采用功率谱密度函数对脉动风速进行模拟，为模拟出斜拉索所处的脉动风环境，采用Davenport脉动风速谱进行人工风场模拟，其密度函数为

(2)

(3)

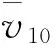
1.3 脉动风场模拟方法

文中采用自回归模型(auto regressive model,AR)方法，模拟拉索在多变量互相关情况下的水平脉动风速时程.M个空间相关的脉动风速时程V(X,Y,Z,t)为

V(X,Y,Z,t)=

(4)

式中：X=[x1,…,xm]T；Y=[y1,…,ym]T；Z=[z1,…,zm]T；(xi,yi,zi)为空间第i点坐标，(i=1,2，…，n)；p为模型的阶数；Δt为模拟时间步长；Ψk为m×m阶的自回归系数矩阵；N(t)为方差为1的独立随机过程向量.

1.4 拉索风场模拟

由文献[9]得广东肇庆高要市百年一遇10 m的设计基本风速为31.6 m/s，取A类地表，地表粗糙度系数为0.12.阅江大桥桥面距离水平面高度40 m，同时主塔最外侧的M24号斜拉索长度为168 m，拉索高度为75 m.研究采用Davenport谱，通过MATLAB软件基于AR模型方法模拟拉索多变量互相关水平脉动风速时程[10]，对此斜拉索进行结构风场模拟，提取脉动风场湍流强度.将此拉索在竖直方向上分为15段，每5 m一段，斜拉索的15个点编号从下往上依次为1～15.

图1为3号节点和14号节点瞬时风速时程的模拟结果，模拟时间步长为0.1 s，共设置2 048步.由图1可知，脉动风为完全不规则的随机脉动，且同一时刻拉索不同位置的风速也不尽相同.脉动风速在-10～10 m/s之间浮动，体现了脉动风速在时间及空间位置上的随机性.同时可见随着高度的增加，平均风速也在递增.为检验水平脉动风速时程模拟结果是否正确，在上述节点中选取3号点的模拟结果进行谱分析，将其与Davenport目标谱进行对比，同时对1，2节点与1，15节点之间进行互相关分析，探索其在空间上的相关性.

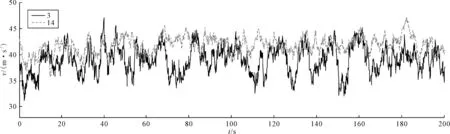
图1 3，14号节点瞬时风速时程

图2为3号节点水平脉动风速度的模拟谱与Davenport目标谱的比对情况，模拟谱没有出现发散现象，其波动表现与目标谱趋势保持一致，尤其在0.1～10 Hz这一区间，这说明模拟的脉动风速时程较为准确，与实际风场情况较为吻合.图3～4为模拟斜拉索几个点之间的互相关函数，点1、2间的相关系数为0.88，点1、15间的相关系数为0.39，可见实际两点间相距越远，其相关性越弱，而1，2号点相距越近，两者相关性越好，反映了实际脉动风速的空间性.

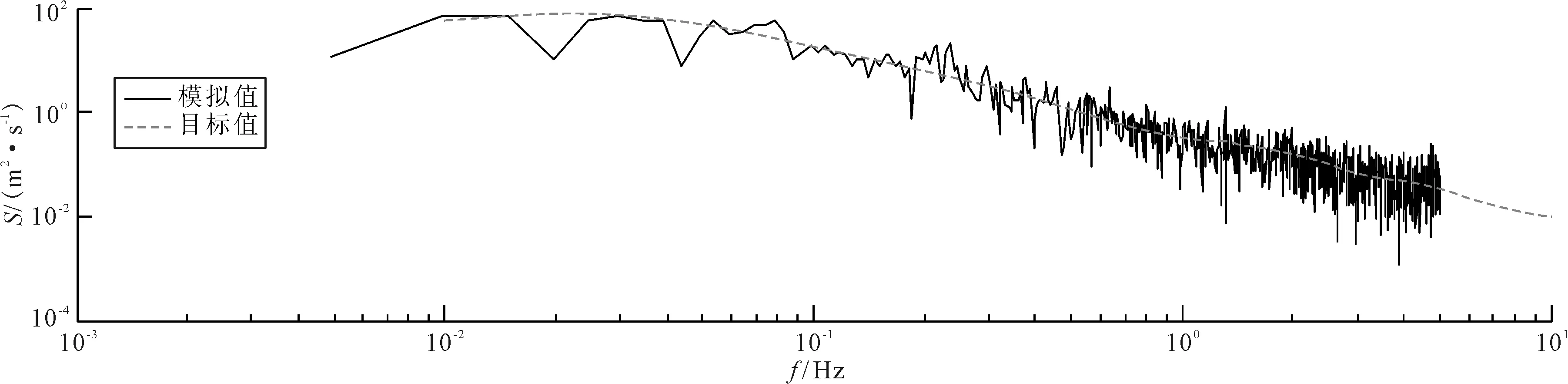
图2 3号节点脉动风速模拟谱与目标谱

图3 1，2节点间互相关函数

图4 1，15节点间互相关函数

2 数值分析模型

风雨振大多发生在中等降雨、中等风速(8～18 m/s)情况下，故本文选择的模拟风速为15 m/s.同时，根据相关文献研究证明，拉索倾角α=30°，风向角β=30°～35°是最易发生风雨激振的情况，并且水线位于拉索的迎风一侧，位置角为40°，对拉索的振动影响最大，拉索的振动幅度会显著增大[11-12].故文中模型工况选择拉索倾角30°，风向角35°，水线角为45°.各角度含义见图5.拉索高度取120 m，直径取0.15 m，流域长、宽、高分别取为65，90，60 m，此模型为阅江大桥M16号斜拉索.

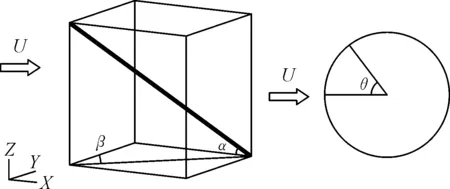
图5 拉索倾角、风向角、拉索表面位置角

在目前斜拉索模型试验中在斜拉索表面贴人工水线，或者数值流体计算时斜拉索表面的水线，一般采用理想的几何水线形状，如矩形、半椭圆形、半圆形等，同时在数值模拟及相关实验中假定水线模型的形状和位置沿斜拉索的轴向是均匀垂直分布的.研究对象采用圆弧形水线，其中水线的弦长b为20 mm，水线高h取10 mm，水线大小及形状见图6.

图6 水线形状及尺寸

考虑拉索空间姿态，流体部分采用非结构化网格划分，对拉索表面网格进行加密以控制边界层，拉索表面最小网格长度设为0.01 m，覆面层网格划分10层，拉索表面网格控制为三棱柱网格，以减小拉索表面网格扭曲率，其他位置采用四面体网格，见图7.湍流模型选用RNGk-ε模型，由MATLAB计算提取结果计算湍动能k取值8.977 m2s-2及比耗散率520.97 Hz.

图7 网格划分

由于缺乏风洞试验条件，为验证数值风洞模型计算准确性，采取该建模思想对同济大学土木实验室的试验模型进行建模[13]，选取拉索倾角α=90°，风速为35 m/s的工况，求解此工况下的拉索风阻系数，与物理风洞试验进行对比，对比结果见表1.将计算结果与试验结果对比发现，采用此计算模型对流场部分进行模拟是可行的.

表1 数值计算与试验结果对比

对斜拉索建模，采用六面体网格划分，考虑斜拉索索力，采用降温方式模拟阅江大桥M16号斜拉索的计算成桥索力5218.3 kN，拉索两端固结.

3 拉索风雨激振数值模拟

利用workbench针对上述计算的风场工况、拉索的空间姿态对钢索及CFRP索进行风雨激振分析[14].流体计算部分采用FLUENT软件，考虑拉索在风场中的几何非线性，拉索部分采用workbench中的瞬态动力学分析(transient structural)模块进行计算.CFRP索和钢索的替换采用等轴向强度原则，即Acσc=Asσs(σ为材料的容许应力).

为方便对比研究，分别对钢索及CFRP索在15 m/s风速的相同工况下，带固定人工水线及不带人工水线两种情况进行风致振动分析，研究人工水线对拉索风致振动的影响，图8为从流体计算部分提取的两类索在z=30 m截面处的表面风压变化图，横坐标为拉索表面的周向角度.

a)钢索

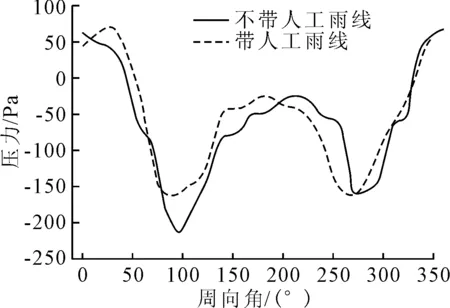
b)CFRP索图8 索表面风压变化

由图8可知，粘贴人工水线之后，两类拉索的表面风压分布均发生了改变，压力最大处由迎风面发展到人工水线周围，最大压力较不粘贴人工水线有一定提高，最大拉力仍出现在拉索两侧，拉索周围风压场重新分布.相比而言，CFRP拉索改变较小，钢索受人工水线影响更大，CFRP拉索受人工水线的影响较小.在此基础上，继续研究拉索振幅变化情况，在此仅列出1秒内振幅变化情况方便对比.

图9～10为不带人工水线钢索三向、带人工水线钢索三向和钢索总的位移时间曲线图.钢索在15 m/s的风速下，不贴人工水线钢索的振动最大位移约为0.79 m，张贴人工水线后拉索由于截面形式改变，索表面流场重分布，且在三个方向的位移均有增大，总位移最大值也达到0.825 m，增幅达到4.43%.同时两者对比可以发现，拉索振动周期并未有太大改变，相位角也未发生改变.观察三个方向位移值增量，在Y轴方向，拉索的振动振幅增加较为明显.

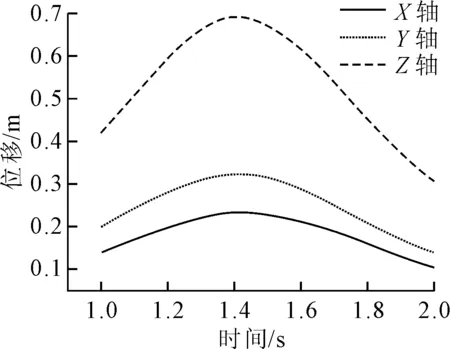
a)不带人工水线

b)带人工水线图9 钢索三向位移时间曲线

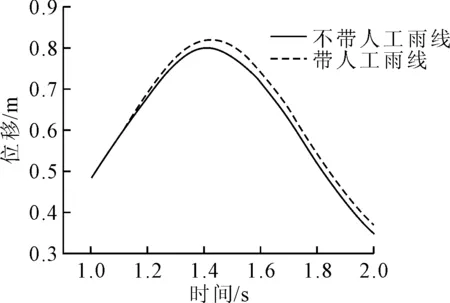
图10 钢索总位移时间曲线

图11～12为不带人工水线CFRP索三向、带人工水线CFRP索三向和CFRP索总的位移时间曲线图.由图11～12可知，CFRP索在15 m/s的风速下，不贴人工水线钢索的振动最大位移约为0.148 m，张贴人工水线后拉索由于截面形式改变，索表面流场重分布，总位移最大值达到0.151 m，增幅为2.03%.同时两者对比可以发现，拉索振动周期并未有太大改变，相位角也未发生改变.同样由于流场分布改变引起索表面压力的分布改变，拉索在Y方向的位移增幅相对明显.与钢索相比，在同样的工况条件下，CFRP索的风雨激振现象相对较弱，且位移增幅也较小，CFRP索的振动频率比钢索要快近两倍.同时，不考虑人工水线，CFRP索在此工况下，相对传统钢索，风振效应有较好的提高.

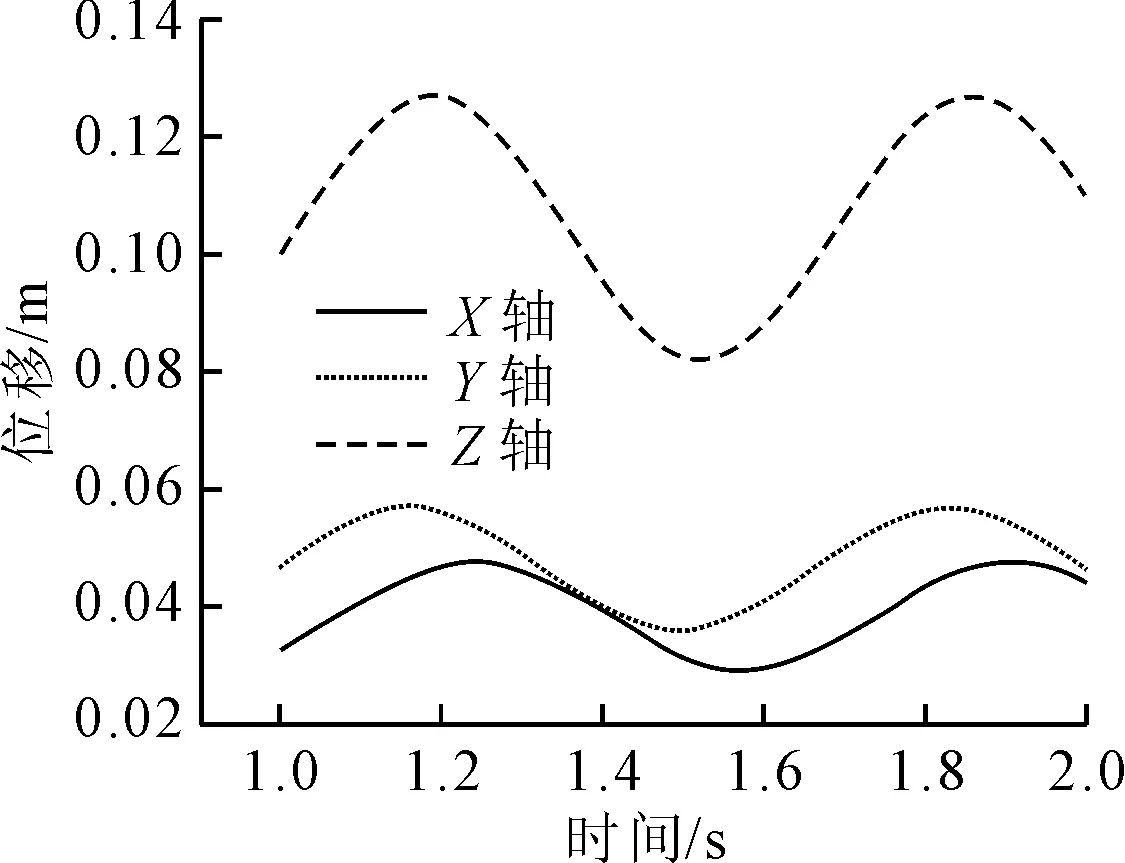
a)不带人工水线

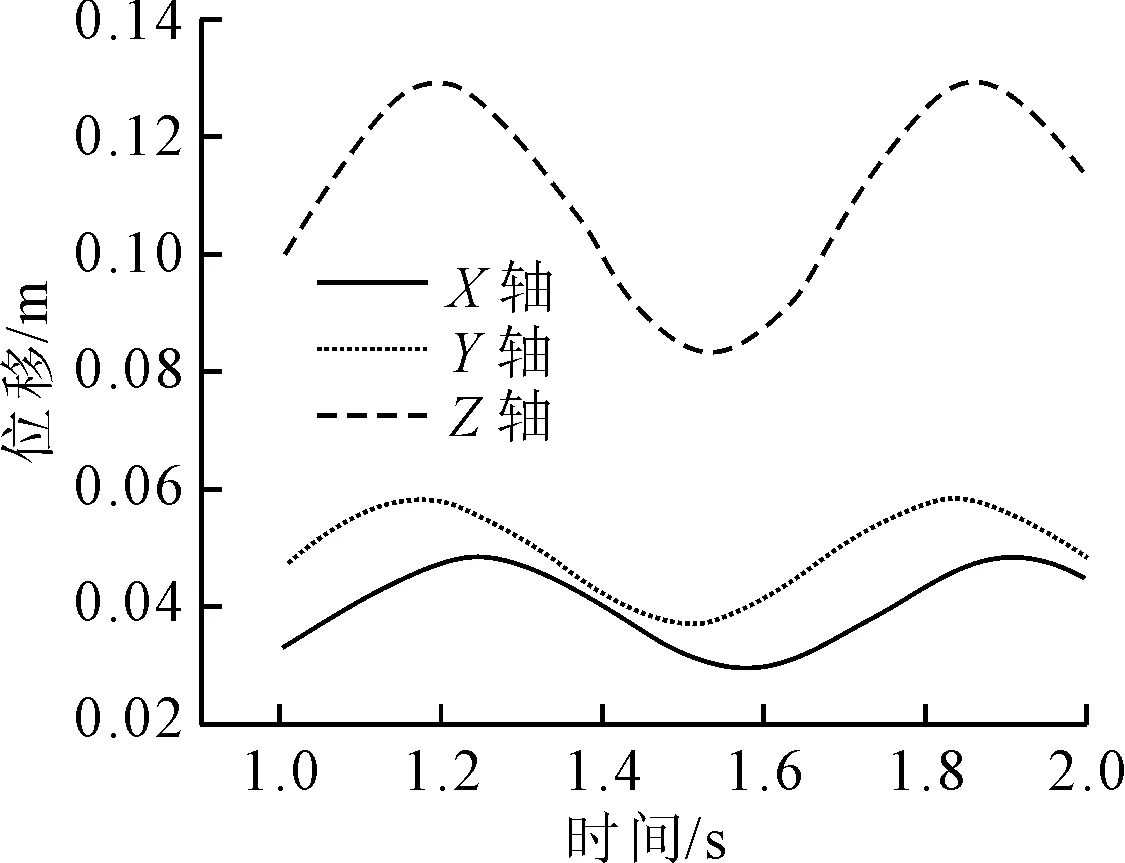
b)带人工水线图11 CFRP索三向位移时间曲线

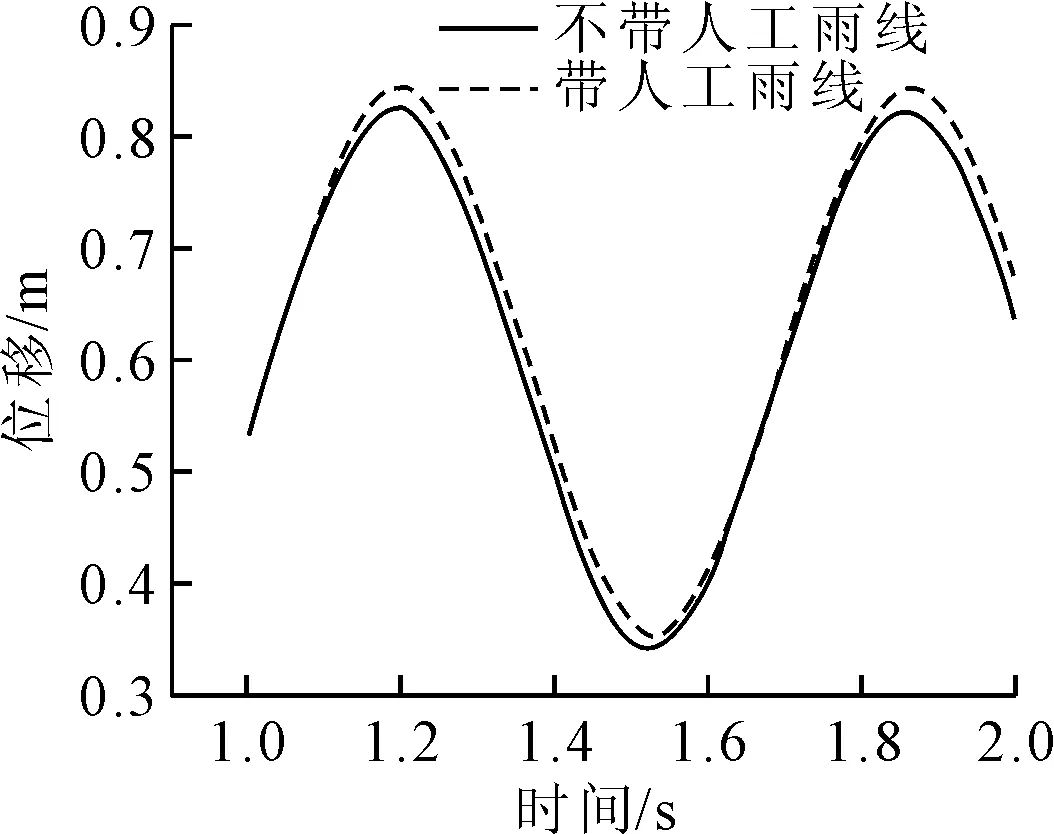
图12 CFRP索总位移时间曲线

4 结 论

1) 对于α=30°，β=35°的风场工况，CFRP索振动最大位移为同类工况下传统钢索的最大位移的1/5，风振效应有良好的改善.

2) 在设置人工水线后，两类索周围流场、风压场重分布，最大压力处出现在水线附近，传统钢索周围风压场受水线影响波动较大.

3) 在设置人工水线后，两类拉索振幅均有增加，传统钢索增幅较CFRP拉索更大，振动频率改变较小.

总体来说，CFRP索对比传统钢索而言，在风雨激振响应上表现更好.但CFRP索的振动频率相对于传统钢索更快，有一定的疲劳隐患.结论能对CFRP索在未来的桥梁应用中提供理论参考，迎接桥梁建设向更大跨径发展的历史趋势.

[1]张新军，孙海凌.超大跨度斜拉桥空气静力和动力稳定性研究[J].中国工程科学，2014,16(3):50-58.

[2]臧华，刘钊，吕志涛,等.CFRP筋用作斜拉桥拉索的研究与应用进展[J].公路交通科技，2006,23(10):70-74.

[3]吕志涛，梅葵花.国内首座CFRP索斜拉桥的研究[J].土木工程学报，2007,40(1):54-59．

[4]ZHANG X J, YIN D L. Wind-resistant performance of cable-supported bridges using carbon fiber reinforced polymer cable[J]. Wind and Structures,2007,10(2):121-133.

[5]KAO C S, KOU C H, XIE X. Static instability analysis of long-span cable-stayed bridges with carbon fiber composite cable under wind load[J]. Tamkang Journal of Science and Engineering,2006,9(2):89-95.

[6]RUSCHEWEYH H P. The mechanism of rain-wind-induced vibration[C]. Wind Engineering into the 21st Century, Balkma, Rotterdam,1974.

[7]YAMAGUCHI H. Analytical study on growth mechanism of rain vibration of cable[J]. Journal of Wind Engineering and Industrial Aerodynamics,1990,33(1):73-80.

[8]张希黔，葛勇，严春风,等.脉动风场模拟技术的研究与进展[J].地震工程与工程振动，2008,28(6):206-212.

[9]中华人民共和国交通部.公路桥梁抗风设计规范:JTG/T D60-01—2004[S].武汉：武汉理工大学出版社，2004.

[10]张田，夏禾，郭薇薇.基于多维AR模型的桥梁随机风场模拟[J].中南大学学报(自然科学版)，2012,43(3):1114-1121

[11]GU M, DU X Q. Experimental investigation of rain-wind-induced vibration of cables in cable-stayed bridges and its mitigation[J]. Journal of Wind Engineering and Industrial Aerodynamics,2005,93(1):79-95.

[12]黄贻凤.带水线的斜拉索气动特性数值分析[J].华东交通大学学报，2015,32(5):16-18.

[13]林志兴，杨立波，李文勃,等.斜拉索顺桥向风阻系数的试验研究及数值模拟[C]∥2004全国结构风工程实验技术研讨会论文集，长沙：中国土木工程学会，2004.

[14]王春江，陈锋，周岱.风场中长单索结构流固耦合效应的动力学分析[J].力学季刊，2010,31(2):213-219.

Numerical Simulation of Rain-wind Induced Vibration for CFRP Cable Considering Fluid Structure Interaction

YANG Jixin1)LI Jianhua1)YU Yue2)SUN Tingting1)LIU Jie1)

(School of Transportation, Wuhan University of Technology, Wuhan 430063, China)1)(CCCC Second Highway Consultant Co. Ltd., Wuhan 430050, China)2)

Based on the construction of Yue Jiang Bridge, adapting Davenport spectrum for fluctuating wind, the horizontal wind velocity time series are simulated by the auto regressive model. Combining the wind field condition, the rain-wind induced vibration on fluid-structure interaction for steel cable and CFRP cable is calculated and simulated by considering the condition that is most likely to produce rain-wind induced vibration. The results show that the performance of CFRP cable is better than that of conventional cable, but the vibration frequency of CFRP cable is faster.

auto regressive model; wind field; fluid structure interaction; CFRP cable; rain-wind induced vibration

2017-03-30

*国家自然科学基金项目(51408446)、安徽省高校自然科学重点项目(KJ2016A448)资助

U441

10.3963/j.issn.2095-3844.2017.03.017

杨吉新(1964—)：男，博士，教授，博导，主要研究领域为桥梁结构与计算力学