DRAGON&DONJON程序在MSR中堆芯燃耗计算的适用性

赵文博 谢金森 谢 芹 陈珍平 曾文杰 刘紫静 何丽华 于 涛

DRAGON&DONJON程序在MSR中堆芯燃耗计算的适用性

赵文博 谢金森 谢 芹 陈珍平 曾文杰 刘紫静 何丽华 于 涛

（南华大学 核科学与技术学院 衡阳 421001）

DRAGON&DONJON组件-堆芯“两步法”程序通过合理简化，理论可适用于任何堆芯与工况。使用蒙特卡罗方法RMC (Reactor Monte Carlo code)、MCNP (Monte Carlo Neutron Particle transport code)程序验证DRA&DON程序是否能够承担快/热谱型熔盐堆(Molten Salt Reactor, MSR)焚烧TRU、ThU燃料燃耗计算。选出熔盐增殖堆(Molten Salt Breeder Reactor, MSBR)与熔盐锕系元素再循环和嬗变堆(Molten Salt Advanced Reactor Transmuter, MOSART)堆型进行比较，同时分别利用RMC程序验证DRAGON程序组件燃耗计算的准确性，利用MCNP程序验证DRAGON程序组件均匀化方法以及DONJON程序截面调用和程序全堆扩散的准确性。结果表明，组件燃耗计算中，TRU和ThU燃料满足燃耗计算要求；堆芯临界计算中，快/热谱堆芯计算误差均小于0.001。证明DRA&DON程序可以胜任快、热谱型MSR焚烧TRU、ThU燃料的物理计算任务。

熔盐堆，组件均匀化，ThU燃料，TRU燃料

熔盐堆(Molten Salt Reactor, MSR)堆芯物理计算的相关分析程序较少，现今研究主要依靠多种物理计算程序相互校核完成MSR堆芯计算。其中可分为蒙特卡罗(Monte Carlo method, MC)与确定论两类程序，而MSR在线处理过程周期短（熔盐堆实验(Molten Salt Reactor Experiment, MSRE)堆中每487s去除惰性气体）[1‒2]，使用MC方法进行燃耗计算，需对每次在线处理设立燃耗步，计算耗时过长；然而与MC方法相比，确定论方法采用截面近似处理以及共振近似处理等原因，尤其本次研究中需要涉及TRU燃料多共振核素的中子输运计算，可能产生较大误差。因此本文主要通过使用蒙特卡罗程序MCNP (Monte Carlo Neutron Particle transport code)和RMC (Reactor Monte Carlo code)作对标校核程序，验证确定论程序DRAGON&DONJON能否胜任快/热谱型MSR堆芯焚烧TRU、ThU燃耗计算任务。因燃耗计算主要与中子能谱和截面数据有关，考虑几种程序的适用性，本文计算均在堆芯无在线处理、熔盐不流动的静态环境假想条件下进行，因而未考虑缓发中子先驱核流动性的相关计算[3]。

DRAGON&DONJON程序均为加拿大蒙特利尔技术学院研制的反应堆物理数值计算程序[4]。其中DRAGON为组件计算程序，DONJON为堆芯计算程序。组件-堆芯“两步法”是目前工业界广泛应用的反应堆核设计方法，它在保证一定精度的前提下，提供了可接受的计算代价。

在“两步法”中，组件计算主要用于产生不同工况下的组件均匀化少群常数，这些离散工况的均匀化少群常数通过特定的方法进行拟合（插值）可用于任意工况堆芯计算。因此DRAGON&DONJON程序可以实现MSR在线化学处理过程，更真实的模拟MSR运行工况。RMC与MCNP均为蒙特卡罗输运程序，RMC为清华大学研发设计[5]。

1 MSR堆型材料选取与简化

本文选取熔盐增殖堆(Molten Salt Breeder Reactor, MSBR)与熔盐锕系元素再循环和嬗变堆(Molten Salt Advanced Reactor Transmuter, MOSART)进行研究分析。TRU燃料熔盐选取MOSART熔盐58NaF-15LiF-27BeF2(1.5 mol% Pu + MA)[6]进行分析，ThU燃料熔盐选取MSBR熔盐71LiF-16BeF2-12.7ThF4-0.3235UF4[7]、MSFR熔盐77.5LiF-20ThF4-2.5233UF4[8]进行分析。它们的燃料熔盐进出口温度较低，两种堆型平均温度相近，同时堆芯快热能谱区分明显，方便分析与比较。由于MSBR与MOSART实际堆型较为复杂，为方便研究，需要对堆芯进行相应简化。

1.1 MSBR熔盐堆简化

MSBR堆芯概念设计模型如图1所示[7]，MSBR堆芯活性区高度为3.96m，堆芯总体半径为3.38m。MSBR堆芯由中心控制棒系统、ZONE-1区、ZONE-2区两区组件组成，组件尺寸为10.16 cm× 10.16 cm，组件中石墨作为导流通道和慢化剂作用。ZONE-1区为燃料体积占13.2%的组件构成；ZONE-2区在ZONE-1堆芯外围包裹了一圈燃料体积占37%的组件，能够有效搅混内外燃料熔盐流速，展平堆芯功率；37%的组件外围包裹了近30cm石墨栅栏，栅栏与外侧石墨反射层留有6cm缝隙，供燃料熔盐流过；在外围为石墨反射层厚度为76cm。

图1 MSBR堆芯结构Fig.1 MSBR reactor core structure.

燃料组件结构较为复杂，为方便分析和简化计算，采用面积等效法，对组件模型进行简化，简化模型见图2。其中，中心为燃料孔道，外部为石墨慢化剂。此外因石墨栅栏无法用程序建模，因此在模拟中直接采取搅混计算，全堆简化后模型如图3所示。

图2 MSBR组件简化模型 (a) ZONE-1，(b) ZONE-2Fig.2 MSBR simplified assembly model. (a) ZONE-1, (b) ZONE-2

图3 MSBR简化堆芯模型Fig.3 MSBR simplified model.

1.2 MOSART熔盐堆简化

MOSART堆芯概念设计模型如图4(a)所示[6]，MOSART堆芯呈罐式结构，堆芯高度为3.6m，堆芯直径为3.4m。整体结构总体可以分为三层：第一层为罐内充满燃料熔盐圆柱；第二层为包裹燃料熔盐的30cm石墨反射层，防止中子泄漏；第三层为最外围20cm不锈钢堆芯壳体，因此堆芯堆型可以简化为如图4(b)所示。为更有效对堆芯进行分析，简化计算任务，因此通过调整堆芯高度，去除堆芯上下两端较为复杂的锥形结构，经MCNP程序对两模型校算，最后得到MOSART简化模型如图4(c)所示。因不锈钢对快中子影响较小，因此在简化模型中忽略不计，堆芯活性区高度为360cm，堆芯活性区半径170cm，石墨厚度为30cm。由于MOSART堆芯无组件结构，MOSART组件可假设为纯燃料无限高圆柱，组件边界采用白边界处理，因此组件半径可任意设置，考虑计算任务与时间，组件半径选取为3cm。

图4 MOSART简化过程(a) 堆芯实际模型，(b) 计算模型，(c) 简化模型Fig.4 MOSART simplified model. (a) MOSART core actual model, (b) Actual calculation model, (c) Final simplified model

2 DRAGON&DONJON程序准确性验证

2.1 DRAGON程序组件燃耗计算校算

首先验证DRAGON程序组件燃耗计算的准确性，分别选取MSBR和MOSART堆芯组件进行验证，材料截面库以ENDF/B-VII.0为母库，热谱堆芯使用172群WIMSD格式截面库，快谱堆芯使用适用于ERANOS快堆的315群DRAGLIB格式截面库，共振处理使用Stamm’ler[9]方法。

图5为TRU燃料在快热谱型堆型组件的燃耗结果，以下数据均为在MSR中焚烧400d数据结果。从图5可以看到，在快、热谱堆芯MSBR组件中，TRU燃料在热谱堆芯中焚烧结果误差会随着时间逐渐增大，主要因为各核素种类增多，核素间共振干涉增强，同时随着燃耗深度增加，数据库燃耗链的误差逐渐累积，这两个原因共同造成燃耗误差逐渐增大。截取其中部分数据，燃烧至225d时，kinf结果误差为0.00613，此时燃耗深度为204.621GW·d·t−1，各燃料核素平均相对误差为1.29%，单一燃料核素最大相对误差为3.56% (242Pu)。烧至365d时，kinf结果误差为0.01497，燃耗深度为331.941GW·d·t−1，各燃料核素平均相对误差为2.06%，单一燃料核素最大相对误差为4.43% (242Pu)。可以看出，虽然组件无限增殖系数kinf在300d后误差较大，但各TRU核素之间误差较小，此时已经远超过传统燃耗计算中的燃耗深度，在模拟燃烧60GW·d后（此处燃烧为60d，该燃耗深度为压水堆最大燃耗深度），DRAGON程序与RMC程序给出的有效增殖因数kinf的最大误差为0.00336，在60GW·d·t−1燃耗深度下，两者给出的各TRU核素积存量的平均相对误差为0.46%，最大相对误差为1.27% (243Am)，且两程序计算趋势一致，因此可以说明DRAGON程序可以胜任热谱堆芯多共振核素燃料计算任务，并能够为在深燃耗情况下，提供较好的各TRU核素积存量变化数据；TRU燃料在快谱堆芯组件焚烧400d中可以看到，组件kinf误差维持在0.007‒0.008，误差主要来源于各燃料核素快谱处吸收截面变化复杂，同时存在多核素共振干涉效应，这两个原因共同造成两程序的计算误差，然而从结果可以看到，在组件焚烧400d结束时（燃耗深度为163.692GW·d·t−1），各TRU核素积存量平均相对误差为0.462%，单一燃料核素最大相对误差为1.34% (244Cm)，说明两程序结果变化趋势一致，同时证明虽然临界计算误差较大，但各核素燃耗链计算准确，说明DRAGON程序可以模拟TRU核素在快谱堆芯中焚烧的燃耗计算。

图5 TRU燃料DRAGON&DONJON与RMC程序计算结果比较 (a) 热谱，(b) 快谱Fig.5 TRU fuel comparison of calculation results between DRAGON&DONJON and RMC. (a) Thermal spectrum, (b) Fast spectrum

图6 中ThU燃料组件两程序kinf曲线符合结果较好。在热谱堆芯组件中，焚烧至400d结束时，MSBR燃料燃耗深度为52.283GW·d·t−1，误差为0.01823，但燃料核素积存量平均误差为1.05%，最大误差为2.98% (233Pa)，同时此时组件kinf已经远小于1，无法达到临界，kinf=1时为燃烧至105d，燃耗深度为13.296GW·d·t−1，此时误差仅为0.00326，核素积存量平均误差为0.89%，最大误差为1.54% (233Pa)；MSFR燃料燃耗深度为27.868GW·d·t−1，误差为0.00761，燃料核素积存量平均误差为1.385%，最大误差为3.04% (234U)，此时组件kinf同样远小于1，临界时燃耗深度为15.482GW·d·t−1，误差仅为0.00372，燃料核素积存量平均误差为1.063%，最大误差为2.27% (234U)，kinf曲线变化一致，因此可以说明DRAGON程序可以在热谱MSR中进行ThU燃料燃耗计算。在快谱中MSBR型燃料无法满足临界要求，因此仅使用MSFR燃料进行验证，从图6中可以看出，曲线变化趋势一致，焚烧至400d结束时，燃耗深度为16.099GW·d·t−1，组件kinf误差仅为0.00371，燃料核素积存量平均误差为1.17%，最大误差为3.59% (234U)，证明DRAGON程序可以在快谱MSR中进行ThU燃料燃耗计算。综合以上结果，虽然总体ThU燃料燃耗深度较小，但已经满足快热谱MSR计算范围的要求，同时在MSR需要计算的范围内，组件燃耗计算结果较好，燃料核素积存量计算准确，因此可以证明DRAGON程序较好地模拟ThU燃料在快、热谱MSR中的燃耗计算。

图6 ThU燃料DRAGON&DONJON与RMC程序计算结果比较 (a) 热谱，(b) 快谱Fig.6 ThU fuel comparison of calculation results between DRAGON&DONJON and RMC. (a) Thermal spectrum, (b) Fast spectrum

2.2 DRAGON&DONJON程序组件-堆芯“两步

法”简化方法验证

组件-堆芯“两步法”，可以对堆芯进行了简化计算，减少计算任务，同时可能因简化的步骤产生误差，因此通过对MSBR与MOSART零燃耗临界计算验证，确定DRAGON&DONJON程序“两步法”计算方法准确性，同时确定堆芯简化模型合理性。具体步骤如下。

2.2.1 MSBR全堆校算

根据MSBR堆芯设计，在使用DRAGON程序进行少群截面生成时，主要把MSBR分为三区，分别为：ZONE-1、ZONE-2区、石墨栅栏与石墨反射层中石墨栅栏与之间缝隙的燃料均匀化截面，以及石墨反射层少群截面的计算。具体简化过程见图7。生成均匀化截面后，利用DONJON程序建模并调用均匀化少群截面计算，DONJON全堆模型见图8。

图7 MSBR组件均匀化模型 (a) 燃料组件，(b) 堆芯边界Fig.7 MSBR assembly homogenization. (a) Assembly homogenization, (b) Core boundary reflector homogenization

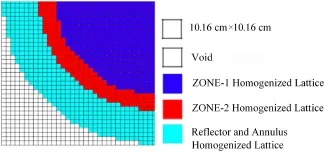
图8 DONJON程序1/4 MSBR堆芯计算模型Fig.8 1/4 MSBR core calculation model.

以ThU燃料作为参考依据，经过上述计算过程，各阶段结果见表1。从结果可以看出，与MCNP计算结果相比，DRAGON程序组件临界计算中误差小于0.002。全堆计算中，DONJON调用经DRAGON均匀化、并群的组件，同时合理地考虑了超栅尺寸的选取，并以真实模型为基础，可以保证DONJON程序步骤中引入误差很小，因此由于ZONE-1区（正误差）与其他区误差（负误差）相互抵消，导致DONJON程序误差仅为0.00053± 0.00035，可见DRAGON&DONJON“两步法”程序可以较好适用于热谱堆芯MSBR中计算。

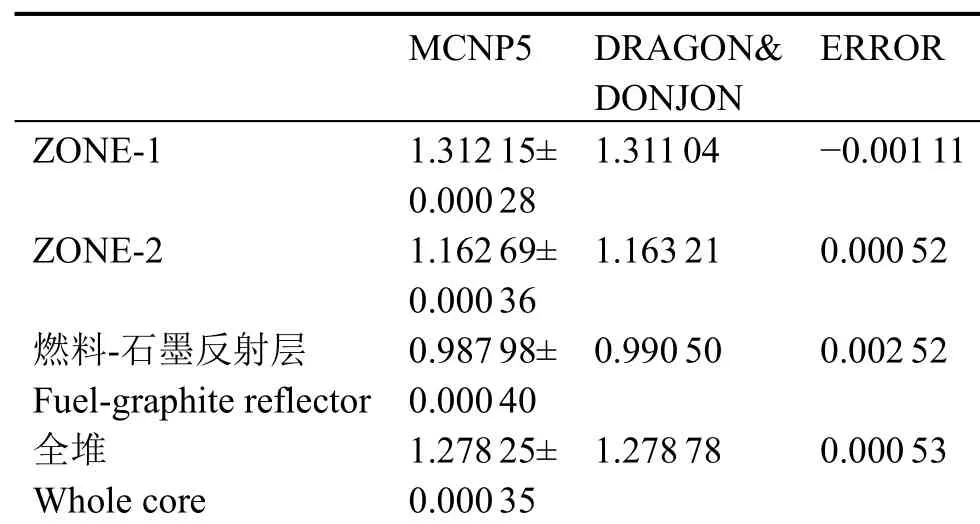
表1 热谱堆芯DRAGON&DONJON“两步法”计算结果误差Table 1 Thermal spectrum core DRAGON&DONJON“two steps” calculation error.

2.2.2 MOSART全堆校算

MOSART为快谱堆芯，堆芯却由石墨包裹，堆芯外围中子能谱变化较大，因截面并群需根据能谱计算，因此使用DRAGON&DONJON程序在对MOSART堆芯进行建模时，需要先计算堆芯能谱分布后对堆芯进行分区。图9为MOSART堆芯分别装载TRU、ThU燃料时，堆芯径向位置能谱分布。从图9可以看到，当半径为0‒140cm时，中子能谱分布几乎不发生变化趋于一致；当半径为140‒200cm时，燃料被石墨慢化，堆芯中热中子通量逐渐增加。

图9 TRU (a)和ThU (b)燃料径向位置能谱分布Fig.9 MOSART energy spectrum distribution of TRU (a) and ThU (b) fuel.

因此堆芯可分为两区进行计算，0‒140cm为ZONE-1区纯燃料区和140‒200cm燃料-石墨反射层区。均匀化方法与MSBR堆芯组件相同，简化为方形无限高少群均匀化组件。两区模型如图10所示，全堆模型如图11所示。

图10 MOSART组件均匀化模型Fig.10 MOSART assembly homogenization.

图11 DONJON程序1/4全堆MOSART堆芯计算模型Fig.11 1/4 MOSART core calculation model.

以ThU燃料做为参考依据，经过上述计算过程，各阶段结果见表2，从结果可以看出，与MCNP程序计算结果相比组件临界计算中DRAGON程序计算结果误差小于0.002，全堆计算中与MSBR堆芯相同，ZONE-1区为负误差，外区为正误差，经过相互抵消，DONJON程序误差仅为0.00029± 0.00013，可见DRAGON&DONJON“两步法”程序可以较好地适用于快谱堆芯MOSART中的计算。

表2 快谱堆芯DRAGON&DONJON“两步法”计算结果误差比较Table 2 Thermal spectrum core DRAGON&DONJON“two steps” calculation error.

3 程序适用性评价总结

从以上结果可以看到：

1) 在准静态情况下，组件燃耗计算中DRAGON程序ThU燃料在快/热谱型MSR中焚烧可以得到较好的计算结果，最大误差小于0.005；TRU燃料虽然在快/热谱型中误差相对较大，但曲线变化趋势一致，误差变化稳定，同时在深燃耗的条件下，依然有较好的核素积存量信息。

2) 从均匀化方法选用与堆芯临界计算结果可以得出，在能够保证DRAGON程序准确结果的前提下，DRAGON&DONJON组件-堆芯“两步法”方法可以用于MSR堆芯计算。

综上所述，本文在准静态近似条件下，针对MSR堆芯，从数据库、组件及堆芯计算进行分析，验证了DRAGON&DONJON程序可以胜任快、热谱型MSR焚烧TRU、ThU燃料的全堆燃耗计算任务。其中验证了包括：截面数据库的适用性、DRAGON燃耗计算正确性、MSR超栅计算方法可行性、DRAGON&DONJON耦合计算适用性、DONJON全堆计算正确性。

1 Bell M J. Calculated radioactivity of MSRE fuel salt[R]. ORNL-TM-2970, USA: Oak Ridge National Laboratory, 1970.

2 张志宏, 夏晓彬, 朱兴望, 等. 含在线处理的熔盐堆源项计算[J]. 核技术, 2014, 37(2): 020603. DOI: 10.11889/ j.0253-3219.2014.hjs.37.020603.

ZHANG Zhihong, XIA Xiaobin, ZHU Xinwang, et al. Source terms calculation for the MSRE with on-line removing radioactive gases[J]. Nuclear Techniques, 2014, 37(2): 020603. DOI: 10.11889/j.0253-3219.2014.hjs.37. 020603.

3 蔡军, 夏晓彬, 陈堃, 等. 熔盐堆中燃料流动对缓发中子的影响分析[J]. 核技术, 2014, 37(3): 030603. DOI: 10.11889/j.0253-3219.2014.hjs.37.030603.

CAI Jun, XIA Xiaobin, CHEN Kun, et al. Study of fluid fuel influence on delayed neutron in Molten Salt Reactor[J]. Nuclear Techniques, 2014, 37(3): 030603. DOI: 10.11889/j.0253-3219.2014.hjs.37.030603.

4 Marleau G, Hebert A, Roy R. A user guide for DRAGON[M]. Canada: école Polytechnique de Montréal, 2007.

5 丘意书, 佘顶, 范潇, 等. 堆用蒙特卡罗程序RMC的全堆计算研究[J]. 核动力工程, 2013, 34(S1): 1‒4.

QIU Yishu, SHE Ding, FAN Xiao, et al. Analysis of full-core calculation of RMC[J]. Nuclear Power Engineering, 2013, 34(S1): 1‒4.

6 Ignatiev V, Feynberg O, Gnidoi I, et al. Progress in development of Li, Be, Na/F molten salt actinide recycler and transmuter concept[C]. Proceedings of International Conference of Asian Political Parties, Nice, France, 2007:75.

7 Robertson R C. Conceptual design study of a single-fluid molten-salt breeder reactor[R]. ORNL-4541, USA: Oak Ridge National Laboratory, 1971.

8 Heuer D, Merle-lucotte E, Allibert M, et al. Towards the thorium fuel cycle with molten salt fast reactors[J]. Annals of Nuclear Energy, 2014, 64: 421‒429. DOI: 10.1016/j.anucene.2013.08.002.

9 Hebert A, Marleau G. Generalization of the Stamm’ler method for the self-shielding of resonant isotopes in arbitrary geometries[J]. Nuclear Science and Engineering, 1991, 108: 230‒239.

Feasibility of DRAGON&DONJON code for MSR core burnup calculation

ZHAO Wenbo XIE Jinsen XIE Qin CHEN Zhenping ZENG Wenjie LIU Zijing HE Lihua YU Tao
(School of Nuclear Science and Technology, University of South China, Hengyang 421001, China)

Background: Simplify DRAGON&DONJON lattice - core “two step” process reasonably, this method can be applied to any reactor and any working condition. Purpose: This study aims at verifying the feasibility of using DRAGON&DONJON physical analysis for burning TRU and ThU fuel in molten salt reactor (MSR) by combination of reactor Monte Carlo code (RMC) and Monte Carlo neutron particle transport code (MCNP). Methods: Both the molten salt breeder reactor (MSBR) and molten salt advanced reactor transmuter (MOSART) reactor were taken as examples for comparison and analysis. RMC program was employed to verify accuracy of burnup calculated by DRAGON program whilst MCNP program was used to verify both the accuracy of lattice homogenization embedded in DRAGON program and the few group cross - section call and diffusion in whole reactor adopted in DONJON program. Results: The results show that DRAGON program can be used in MSR for burning TRU and ThU fuel. The calculation errors of fast spectrum and thermal spectrum diffusion are less than 0.001 in critical calculation. Conclusion: DRAGON&DONJON is suitable for physical analysis of TRU and ThU fuel burning in MSR.

MSR, Lattice homogenization, ThU, TRU

ZHAO Wenbo, male, born in 1992, graduated from East China Univercity of Technology, master student, focusing on reactor physics research Corresponding author: YU Tao, E-mail: yutao29@sina.com

date: 2016-11-28, accepted date: 2016-12-26

TL99

10.11889/j.0253-3219.2017.hjs.40.060602

国家自然科学基金(No.11305088)、湖南省自然科学基金(No.14JJ2088)资助

赵文博，男，1992年出生，2014年毕业于东华理工大学，现为硕士研究生，从事反应堆物理计算研究

于涛，E-mail: yutao29@sina.com

2016-11-28，

2016-12-26

Supported by National Natural Science Foundation of China (No.11305088), Natural Science Foundation of Hunan Province (No.14JJ2088)