多目标差分进化算法在投资组合中的应用

任雪婷，卞京红，张 迷

(西安工程大学 理学院，西安 710048)



多目标差分进化算法在投资组合中的应用

任雪婷，卞京红，张 迷

(西安工程大学 理学院，西安 710048)

针对多目标优化问题，提出一种改进的多目标差分进化算法.在基本的差分进化算法中引入了参数自适应调整操作和可行性规则操作.同时，在综合考虑交易费用的基础上建立多目标投资组合模型，并应用改进算法进行求解.结果表明，改进的多目标差分进化算法得到的多目标投资组合的收益率要高于其他算法得到的收益率.

差分进化算法；多目标优化；投资组合；可行性规则

多目标投资组合问题已经成为金融投资领域的热点研究问题. 美国经济学家Markowitz在1952年提出了投资组合理论[1]，为现代投资组合鉴定了基础. 此后，国内外的一些学者对投资组合问题进行了深入的研究，并且取得了一些有价值的成果[2-5]. 但是，智能优化算在这一方面的应用还比较少. 特别是近几年来，计算机技术在迅猛发展，在金融领域，用计算机来解决实际中的金融问题已经成为了学术界的一种热潮，这就将计算机与金融相结合的研究推向了金融科研与应用的前沿. 目前，遗传算法在这一方面得到了初步的应用，并且取得了一些研究成果. 如攀登等用遗传算法来直接搜寻证券投资组合的有效边界[6]；群等用遗传算法来求解最佳的证券投资组合[7]；刘洪杰等将改进的多模态遗传算法应用于投资组合的决策方案中[8]；任建芳用遗传算法建立随机最优证券投资组合模型[9]等.

差分进化算法(Differential Evolution，DE)是由Rainer Storn和Kenneth Price共同提出来的一种利用浮点矢量编码在连续的空间中进行随机搜索的优化算法[10].在许多复杂的优化问题中得到广泛的应用.Abbass等[11]提出了求解多目标优化问题的Pareto前沿DE算法；Babu等[12]结合罚函数法和权值系数法提出了一种求解多目标优化问题的DE算法；Parsopoulos等[13]提出了一种用于求解多目标优化问题的矢量评估DE算法.然而，这些算法都没有考虑如何保持Pareto最优解的多样性问题，容易过早收敛.因此，本文在考虑交易费用的情况下，建立了多目标优化的投资组合模型，并且将参数的自适应调整策略和可行性规则[14]引入到基本的DE算法中，从而得到了一种改进的多目标差分进化算法(DEMO). 最后用DEMO算法来求解多目标优化的投资组合问题. 通过实证分析得出，改进的多目标差分进化算法在求解多目标优化的投资组合问题时能够取得较好的效果.

1 基于多目标优化的投资组合模型的建立

假设市场上有m种风险资产Ti(i=1,2,…,m)构成投资组合，现在用总额为S的资金作为一个时期的投资. 在投资的过程中，第i种风险资产的平均收益率为ri，预期风险资产的损失率为ui，投资者在进行资产投资时存在一定的风险，本文考虑用m个资产中最大的风险资产来度量总体的风险，假设购买资产T1的资金占总资金S的比重为xi；另一方面，设存进银行的存款利率为定值. 建立的多目标投资组合模型[15]如下：

对于一个资产投资时期内的收益总额记为R，

(1)

对于一个资产投资时期内的总体投资风险(取最大的一个资产的投资风险)记为U，

(2)

因为投资者在进行实际的资产投资时，总是要支付一定金额的交易费[16]，交易费通常规定为：设购买的资产Ti支付的交易费率为qi，当购买的金额不超过给定值μi(i=1,2,…,m)时，则交易费用按μi计算. 所以，当投资者进行比较小规模的投资时，并且在所有投资的资产中某一项资产的投资额不超过给定的值μi时，这项资产的交易费用就会相应的提高，投资者的收益也会相应的减小，并且也会使投资者在该项目上的投资决策直接受到影响，从而使得最终得到的收益收到很大程度的影响. 通过上面的分析可以知道，引入交易费用的概念是十分必要的，因此对上面建立的投资组合的数学模型进行改进，从而就可以得到如下的带有交易费用的多目标投资组合模型：

设购买资产Ti的资金占资金总额S的比重为xi，则需要的交易费用为：

(3)

s.t.∑xi=1,xi≥0,i=1,2,…,m.

因此，投资者在一个投资时期内的纯收益总额为：

(4)

为了使收益尽可能的大，风险尽可能的小，那么该多目标投资组合的数学模型可以转化为：

(5)

s.t.∑xi=1,xi≥0,i=1,2,…,m.

大部分实际的投资组合问题都是包括约束条件的，为了避免投资者对某一项资产的持有量过小或者过大，本文对每一项资产的投资比例xi进行了约束：

ai≤xi≤bi

上式中，ai是下界，bi是上界，i=1,2,…,m.

2 模型求解

2.1 差分进化算法的参数自适应改进

差分进化算法的收敛速度以及稳定性与算法的控制参数有很大的关系，在基本的差分进化算法中，变异因子F和交叉概率CR大多采用的是固定的参数设置或者随机的代数线性变换，这不能很好地适应多目标优化问题的需要. 大量实验表明，对于多目标优化问题，在进化初期，非支配解个数越多，说明种群的多样新越差，这就预示着种群的收敛.

因此，本文提出了一种新的自适应参数调整方法，在种群迭代的初期尽量控制种群中非支配解的数量，保证种群的多样性；在种群进化的后期，群体中个体与个体之间的关系都为非支配关系，并且已经大致收敛于Pareto前沿. 所以，本文根据群体进化的代数来只适应的调整种群向Pareto前沿聚集，具体的自适应调整公式如下所示：

(6)

(7)

2.2 改进的多目标差分进化算法(DEMO)

为了更好的解决多目标投资组合优化问题，本文采用了改进的多目标差分进化算法进行求解，DEMO算法的具体步骤为：

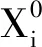
Step2：计算种群中每个个体的适应度值；

(8)

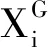
(9)

式(9)中，j=1,2,…，m,m是变量的维数；rand()为[0,1]上均匀的随机序列；交叉概率CR各阶层公式(7)进行自适应的调整；

Step5：将生成的全部的试验个体与父代个体组成一个新的种群QG，在其邻居的集合内，利用轮盘法选择其下一步移动的方向，并计算下一步的位置；

Step6：若G≤Gmax，计算所有个体当前的适应度值f(xi)，根据可行性规则得到最优位置和最优值，若最优值由于当前的最优值，则用当前的最优值与最优位置更新f(X*)和X*,令G=G+1,返回Step2,；否则，转到Step6；

Step7：输出群体最优值与最优位置f(X*)和X*.

3 算法测试

为了验证改进的多目标差分进化算法(DEMO)的有效性，本文将其与目前最具代表性、性能最优的两种算法NSGA-2[17]、MOPSO[18]在四个典型的多目标测试函数Schaffer1、ZDT1、ZDT2和ZDT3中进行对比实验. 图1～4为DEMO、NSGA-2、MOPSO对四个测试函数Schaffer1、ZDT1、ZDT2和ZDT3生成的Pareto front与真实的Pareto front的对比图；表1为各个算法对各个测试函数的实验统计结果，包括和的标准差和均值.

图1 Schaffer1的Pareto front

图2 ZDT1的Pareto front

图3 ZDT2的Pareto front

图4 ZDT3的Pareto front

表1 测试函数的统计结果

对于Schaffer1、ZDT1、ZDT2和ZDT3，从图1～图4可以直观看出，DEMO算法得到的Pareto最优解能够逼近真实的Pareto最优前沿，并且解的分布性也好于其他的算法. 说明提出的改进的多目标差分进化算法具有良好优化性能.

从表1可以看出，DEMO在函数Schaffer1、ZDT1、ZDT2和ZDT3上的多样性指标都是最小的，这说明DEMO算法在保持种群多样性方面要优于其他三个算法，并且得到的Pareto最优解集也有更加均匀的分布性和更加广泛的覆盖范围.

从以上的分析可以看出，改进的多目标差分进化算法能够更加稳定的收敛到真实的Pareto前沿，并且能够在保持算法收敛性的同时改善解的分布性.

4 用DEMO算法进行实证研究

本文选取了60支在2015年1月5日～2015年6月30日的实际股票数据进行研究，将这段时间的开盘价、收盘价和涨幅作为数据集合，对算法的在处理本文建立的多目标投资组合问题时的性能进行验证.

参数设置：种群规模为100，最大进化代数为1 000，变异系数最大值设置为0.9，变异系数最小值设置为0.5，交叉概率最大值设置为0.7，交叉概率最小值设置为0.3.DEMO、NSGA-2、MOPSO 在多目标投资组合优化中的仿真结果分别如表2和图5所示.

表2 日收益率比较

经过算法仿真实验对比，本文选取了两个优化效果比较好的算法DEMO算法和NSGA-2算法，并且将根据本文建立的多目标投资者模型计算得到的最优的投资组合在2015年1月5日～6月30日的116个日收益率和实际的日收益率进行比较.图5为10个交易日的累积收益率的对比结果图，可以看出，改进的多目标差分进化算法(DEMO)要比NSGA-2算法得到的收益率好，并且DEMO算法的日平均收益率要比NSGA-2的日平均收益率高5.89%. 因此，本文提出的改进的多目标差分进化算法能够取得较好的结果.

图5 10个交易日累积的收益率对比图

5 结 语

本文提出了一种改进的多目标差分进化算法(DEMO)，将参数自适应调整操作和可行性规则引入到差分进化算法中，从而提高了基本的差分进化算法的有效性和鲁棒性，并且将改进后的多目标差分进化算法应用到多目标投资组合中. 通过实证研究得出，根据改进的算法可以得到股票的投资比例，并且计算出股票的收益率. 结果表明，改进的多目标差分进化算法得到的多目标投资组合的收益率要高于其他算法得到的收益率，从而验证了本文提出的算法可以有效地用来解决多目标投资组合问题.

[1] MARKOWTTZ H. Portfolio selection [J]. Journal of Finance, 1953, 7: 77-91.

[2] KENDALL G, ROLLINS S. Advanced project portfolio management and the PMO [M]. Florida: J Ross Publishing, 2003.

[3] 刘召军, 高兴宝. 融合自适应混沌差分进化的粒子群优化算法[J]. 纺织高校基础科学 学报, 2015, 28(1): 116-123.

[4] 胡日东. 组合证券投资优化模型的比较研究[J]. 运筹与管理, 2001, 10(1): 99-103.

[5] 万丽英, 李兴斯, 张新芬. 证券投资组合一种多目标优化模型及其算法[J]. 数学实践与认识, 2010, 40(24): 9-14．

[6] 攀 登, 吴冲锋. 用遗传算法直接搜索证券组合投资的有效边界[J]. 系统工程学报, 2002, 17(8): 364-367.

[7] 周 群, 孙德宝. 遗传算法求解最佳证券投资组合[J]. 科技进步与对策, 2001, 18(3): 146-148.

[8] 刘洪杰, 王秀峰, 王治宝. 改进的多模态遗传算法及其在投资组合中的应用[J]. 控制与决策, 2003, 18(2): 173-176.

[9] 陈科燕, 肖冬荣. 基于遗传算法的最优证券投资组合模型[J]. 南京气象学院学报, 2003, 26(5): 707-711.

[10] DEB K, PRATAP A, AGARWAL S,etal. A fast and elitist multi-objective genetic algorithm: NSGA-Ⅱ[J]. IEEE Trans on Evolutionay Computation, 2002, 6(2): 182-197.

[11] ABBASS H A, SARKER R. The pareto differential evolution algorithm [J]. International Journal on Artificial Intelligence Tools, 2002, 11(4): 531-552.

[12] BABU B V, MATHEW M, JEHAN L. Differential evolution for multi-objective optimization[C] //Canberra: Proceedings of IEEE Congress on Evolutionary Computation, 2003. 2696-2703.

[13] PARSOPOULOS K E, TASOULIS D K, PAVLIDIS N G,etal. Vector evaluated differential evolution for multi-objective optimization[C]//Portland: Proceedings of IEEE Congress on Evolutionary Computation, 2004. 204-211.

[14] 王 凌, 刘 波. 微粒群优化与调度算法[M]. 北京: 清华大学出版社, 2008.

[15] 何 光, 吴 萌. 基于改进粒子群算法的投资组合模型[J]. 计算机仿真, 2013(2): 2019-212.

[16] 刘善存, 邱莞华, 汪寿阳. 带交易费用的泛证券组合投资策略[J]. 系统工程理论与实践, 2013, 23 (1): 22-25.

[17] DEB K, PRATAP A, MEYARIVAN T. A fast and elitist multi-objective genetic algorithms: NSGA-Ⅱ [J]. IEEE Transactions on Evolutionary Computation, 2002, 6(2): 182-197.

[18] COELLO C A C, PULIDO G T, LECHUGA M S. Handling multiple objectives with pratic swarm optimization [J]. IEEE Transactions on Evolutionary Computation, 2004, 8(3): 256-279.

Application of multi-objective DE algorithm in portfolio investment

REN Xue-ting, BIAN Jing-hong, ZHANG Mi

(School of Science， Xi’an Polytechnic University, Xi’an 710048, China)

An improved multi-objective differential evolution algorithm for multi-objective optimization problems was proposed. The adaptive adjustment of the parameters and operation rules are introduced in the basic differential evolution algorithm. A multi-objective optimization model of investment portfolio was built based on the transaction expenses and was resolved based on the improved algorithm. The results showed that the yield of the improved multi-objective differential evolution algorithm for multi-objective portfolio was more than other algorithms.

differential evolution algorithm; multi-objective optimization; portfolio; feasibilit rule

2016-09-26.

陕西省自然科学基础研究计划项目(2014,JM100)；陕西省自然软科学研究计划项目(2014KRM2801)；陕西省教育厅专项科研计划项目(14JK1282)

任雪婷(1990-)，女，硕士，研究方向：智能优化算法、数理统计、数据挖掘等.

TP18

A

1672-0946(2017)03-0343-04