基于模态和谐响应分析的压缩机管系振动分析
陈景春, 张 丽, 杜胜民, 孙 铁, 张素香
(1.辽宁石油化工大学 机械工程学院,辽宁 抚顺113001; 2.中国石油抚顺石化分公司 石油三厂, 辽宁 抚顺113001)
基于模态和谐响应分析的压缩机管系振动分析
陈景春1, 张 丽1, 杜胜民2, 孙 铁1, 张素香1
(1.辽宁石油化工大学 机械工程学院,辽宁 抚顺113001; 2.中国石油抚顺石化分公司 石油三厂, 辽宁 抚顺113001)
往复式压缩机是工业领域里重要装置之一,振动的问题一直存在于往复式压缩机管系中,通过模态和谐响应分析后得到的结果可以进一步弄清楚结构的振动特性。对某油气田平台上往复式天然气压缩机管系振动问题,通过模态分析和谐响应分析的方法发现了管系的固有频率值与激发频率共振区相重合的问题,由此提出改变支撑位置、合理的添加支撑的方法,通过模拟以及现场实验数据得出管系固有频率值确有提高,有效减小振动的幅值,验证了该方法的可行性。
管系振动; 固有频率; 模态; 谐响应
气体压缩机是一种输送气体并提高气体压力的有效装置,是许多行业领域中不可或缺的重要设备之一。经常使用的压缩机按原理可以分为往复式、离心式、轴流式等。其中往复式压缩机拥有应用压力界限大、气体压缩效率高、适应能力强等特点,被普遍应用在石油、化工、新能源、食品、饮料等行业中。由于往复式压缩机工作的间歇特性,很容易导致与其相连接的管系发生振动[1]。除了压缩机本身引起的管系振动之外,管系还会受到外界想不到的外力瞬时冲击,管系就会产生复杂的振动,振动必然将会对整个管系的安全有效运行以及使用寿命产生负面影响,情况严重时会造成不能够预计的经济损失。保守统计,美国以往由于管系振动问题带来的直接损失每年达到100亿之多,我国类似事故也时常发生[2]。因此,如何去克服往复式压缩机管系的振动,是实现往复式压缩机高效、高标准投产运行的关键因素。
1 模态及谐响应分析理论
1.1 模态分析理论
模态分析是用来确定已知结构系统的振动特征的一种方法。利用模态分析可以使结构系统在设计之初预防共振或者以确定的频率值进行强制的振动;能够分析到系统对于各种各样类型的动力载荷是怎样响应的;能够帮助在除此之外的动力学分析中确定求解参数的范围[3-6]。由于系统在受到各式各样载荷时的响应情况取决于结构本身的固有特性,所以模态分析是接下来进行其他动力分析的先决条件。
模态分析分为试验模态分析和计算模态分析两大类,其中试验模态分析是将试验结果与理论分析结果结合起来识别出结构系统的固有频率、振型和阻尼等模态参数[7]。在线性系统中,实际结构系统中均可以离散为n个自由度的振动,相对应的就会有n个物理坐标来描述其参数化模型,其动力学方程为:

系统的无阻尼自由振动方程的矩阵表达式可以表示为:
对于线性结构系统式(2)中[M],[K]均为实数对称矩阵,{x}为管系各点的位移响应向量。对n个自由度的管系结构,其位移向量可以表示为:
管系结构的无阻尼自由振动方程(2)是二阶常系数微分方程组。设各个位移分量作同相位的简谐振动如下:
式中{X}=[X1X2X3…Xn]T是振幅向量,ω为圆频率,φ为相位角。
将式(4)代入式(2)中得到代数方程组
其中([K]-ω2[M])称为特征矩阵。式(5)存在非零向量解的充分必要条件为它的特征矩阵行列式等于零。

ANSYS中提供了很多计算固有频率和主振型的方法,综合各方面的因素本文选取子空间迭代法进行计算。
子空间迭代法的迭代步骤如下:

② 采用同时迭代的方法,对于第r次的迭代结果存在如下表达方式:

建立缩减的p阶广义特征问题
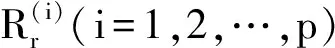
④ 检查精度
指定精度
如此不等式成立,则系统的前k阶固有频率与振型向量分别为:
1.2 谐响应分析理论
谐响应分析的目的在于确定在承受随时间按简谐规律变化的载荷作用下的已知线性结构的稳态响应变化情况,是一种常用的结构动力学分析手段,也被叫做频率响应分析或扫频分析。以计算在不同频率结构下的响应值与频率之间的曲线为目的的谐响应分析,在不考虑初始时激振的瞬态振动情况下,只计算结构稳定之后的稳态受迫振动,达到预测结构连续性动力特征的目的,检验设计是否可以有效的避免共振、疲劳,并且分析由受迫振动所导致的不利影响,如图1所示[9]。

图1 谐响应分析
Fig.1 Harmonic response analysis
谐响应分析的输入载荷(如力、压力、位移)是随时间按正弦规律变化的简谐载荷,其输入的主要参数由频率及幅值两部分组成。频率扫频分析,即众多各异频率及幅值的载荷作用在结构指定位置上所引起的结构响应被谐响应分析[10]。
谐响应分析的输出值包括:节点位移、应力和应变的导出值。通过分析输出值与频率之间的关系曲线,能够得到最大值响应的频率和幅值,作为结构振动机理分析及减振设计的主要依据[11]。
2 某往复式压缩机管系的模态及谐响应分析
2.1 管系振动问题
我国天津某海洋平台上的往复式天然气压缩机二级回流阀在气缸单作用的工况下,管系振动剧烈,噪声超标较为严重,不能长时间运行。该往复式压缩机的标准工况:单作用,转速994 r/min。
压缩机的激发频率的大小是由其转速以及作用形式来确定的。压缩机的型号选定后,压缩机的激发频率就是一个常数,其计算式为[12]:
式中,fo为激发频率,Hz;n为压缩机曲轴转数,r/min;m为压缩机气缸作用方式,单作用,m=1,双作用,m=2。
当气缸以单作用方式运行时,气流脉动的激发频率与机组本身的激发频率一致,皆为16.57 Hz。因此,对机组振动影响较大的前三阶气流脉动激振频率为16.57、33.14 Hz与49.71 Hz。
BH550型综合分析诊断仪的输出信号为被测点的速度时域图及速度频域图,操作简单、使用方便。使用BH550型综合分析诊断仪对高压往复式压缩机管系进行测量,发现在排气洗涤塔与后冷却器连接的管系振动剧烈,振动幅度达到了24.3 mm/s,与标准值25 mm/s非常接近,振动频率主要约为18 Hz。通过和激发频率对比能够得出可能是由于该管系结构本身的固有频率过低导致振动剧烈。
2.2 模态分析
2.2.1 改进前的模态分析 运用Pro/E管道模块根据实际数据创建了管系的三维模型,并导入ANSYS中。设置分析类型为模态分析,选取单元类型为实体单元中的20节点186号单元,并在材料树中根据实际定义材料参数密度ρ=7 850 kg/m3,泊松比μ=0.3,弹性模量E=206 GPa。施加如图2所示的约束力,在Y方向施加全局的重力加速度g=-9.8 m/s2,蝴蝶结为固定约束。
选用智能网格划分, 在网格密度一定的情况下, 同样能够保证有较高的精准度。选用Subspace法对管系结构进行模态分析,获得模型结构的前3阶固有频率值分别为:18.72、25.54、26.44 Hz,相应的振型图如图3所示。

图2 施加约束后的三维模型
Fig.2 3D model with constraint



图3 前3阶振型图Fig.3 The first three order vibration mode
该段管系第一阶固有频率值为18.72 Hz,压缩机单作用时该频率值正好落在激发频率的一阶倍频±10%界限以内,导致该段管系发生低阶共振。分析可知刚度不够是引起低阶结构共振的根本原因,故提高结构的刚度能够有效地降低振动幅度。
2.2.2 改进措施及改进后的模态分析 合理安排支撑位置能够有效提高其结构固有频率值,大大提高这段管系的刚度。由于平台上撬内的空间限制,为了确保它有足够的强度,只能将支架焊接在平台的横梁上。改进后的振动分析模型施加如图4所示的固定约束,改变了原有的支架支撑位置,另外又增设两个支架。

图4 改进后的模型约束
Fig.4 The improved model constraints
经过ANSYS模态分析后获得模型前3阶固有频率值分别为25.55、38.83、40.01 Hz,相对应的振型图如图5所示。
改进后的管系固有频率全部都有大幅度的提升,成功地躲避了激发频率的低阶共振区,有效避免了低阶结构共振。



图5 改进后前3阶阵型图Fig.5 The first three order vibration improved mode
2.3 谐响应分析
在模态分析的基础上,根据平台实际工况在如图6所示弯头处Z方向施加简谐激振力幅值大小为300 N、相位角为30°的约束,指定强制激振频率范围:0~20 Hz,子步数:20,即需要求解1,2,3,…,20 Hz的结果,载荷加载方式选择为阶跃载荷,表示在强制频率的范围内载荷的幅值确保是固定值。采用谐响应分析比较前后不同约束下模型振动幅值变化,在时间历程后处理器POST26中,查看施加简谐力的关键单元节点356号在对应该段强制频率范围内的波动值,改进前后356号单元在X、Y、Z三个方向上的振动位移幅值与该段频率范围内的关系如图7、图8、图9所示。改进前后356号单元在19 Hz时对应在X、Y、Z三个方向的最大振幅值如表1所示。

图6 施加的激振力
Fig.6 The exciting force

图7 改进前后356号单元X方向振动幅值
Fig.7 The amplitude of vibration inXdirection of unit No. 356

图8 改进前后356号单元Y方向振动幅值
Fig.8 The amplitude of vibration inYdirection of unit No. 356

图9 改进前后356号单元Z方向振动幅值
Fig.9 The amplitude of vibration inZdirection of unit No. 356
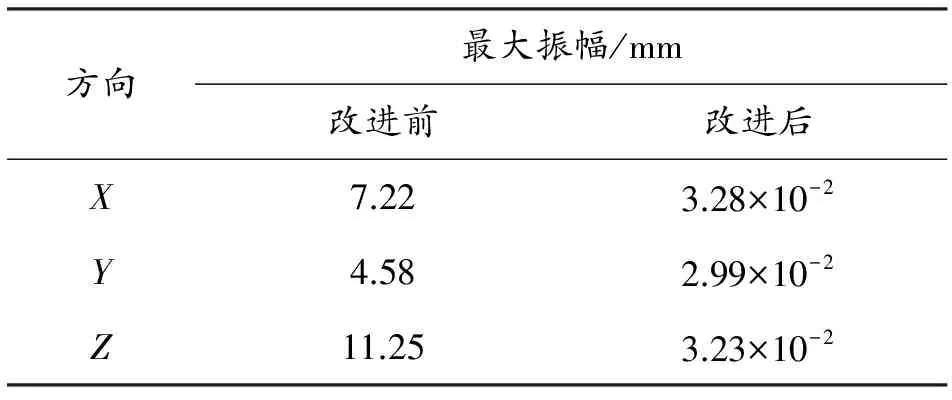
表1 改进前后356号单元三个方向的最大振幅值Table 1 The maximum amplitude values of the three elements before and after the improvement of unit No.356
当施加上述简谐力后,356号单元在0~20 Hz改进前的Z方向振动最为剧烈,振幅最大值在19 Hz时取值为11.25 mm,改进后的最大幅值在24 Hz附近时取值为3.28×10-2mm,位移最大值有了很大程度的减小。其他两个方向上也同样都有很大程度的改进。谐响应分析得到的结果说明了通过改变支撑位置、合理的添加支撑可以有效提高管系固有频率,达到了降低管系振动的作用。
现场实际改进后使用BH550型综合分析诊断仪再次测量原振动剧烈位置,测得结果为3.07 mm/s,相比改进前有明显的减小,现场振动在可控范围内,装置运行平稳。
3 结论
通过模态和谐响应分析方法结合后的结果分析,能够更加准确的反映出结构的动态特性,得到在一段时域内某一部分的具体振动幅值,因此可以采取相应的有效措施,从根源上解决管系振动问题。本文通过有限元分析软件ANSYS分析和研究了往复式压缩机管系的固有振动特性,得到了系统的前三阶主要的固有频率和振型;在此基础上分析了往复式压缩机管系在简谐激振力作用下的响应,得到了往复式压缩机管系振动剧烈部分在简谐力作用下的振动特性。利用分析结果对往复式压缩机管系的结构提出了改进措施,通过实地试验检验,证实了对其进行的仿真分析与结构改进取得了良好效果。
[1] 薛玮飞,杨晓翔,郭金泉.往复式压缩机管道内压力脉动的测试与分析[J].化工机械,2004,31(1):5-7. Xue Weifei, Yang Xiaoxiang, Guo Jinquan. Test and analysis of pressure pulsation in the pipeline of reciprocating compressor[J].Chemical Engineering & Machinery, 2004,31(1):5-7.
[2] 王勇,人白.世界石油化工 100 起特大财产损失事件[J].石油规划设计,1992,3(2):25-32. Wang Yong,Ren Bai. The world's top 100 oil and gas projects in the event of catastrophic loss of oil[J]. Petroleum Planning & Engineering,1992,3(2):25-32.
[3] 郭荣,周鋐.某型轿车白车身试验模态分析及动态特性评价[J].机械设计,2010,27(8):18-22. Guo Rong, Zhou Hong. Modal analysis and dynamic performance evaluation of white body test for a certain type of car[J]. Journal of Machine Design, 2010, 27(8):18-22.
[4] 麻海舰,周鋐.利用白车身振动模态试验对车身动态设计的评价与分析[J].噪声与振动控制,2007,27(4):58-60. Ma Haijian, Zhou Hong. The vibration testing and modal analysis for body in white of a car[J]. Noise and Vibration Control, 2007, 27 (4):58-60.
[5] 许金余,张其顶,宋洪斌,等.基于模态分析的钢结构损伤识别方法研究[J].机械科学与技术,2007,26(2):206-208. Xu Jinyu, Zhang Qiding, Song Hongbin, et al. Steel structural damage detection method based on modal analysis[J].Mechanical Science and Technology, 2007, 26(2):206-208.
[6] Verboven P,Guillaume P,Cauberghe B,et al.Modal parameter estimation from input-output fourier data using frequency-domain maximum likelihood identification[J].Journal of Sound and Vibration,2004,276(3):957-979.
[7] 梁君,赵登峰.模态分析方法综述[J].现代制造工程,2006(8):139-141. Liang Jun,Zhao Dengfeng.Sumary of the model analysis methods[J].Modern Manufacturing Engineering,2006,(8):139-141.
[8] 宋博,李桐宇,王卫强,等. 海洋立管系统严重段塞流瞬态数值模拟[J]. 辽宁石油化工大学学报, 2016, 36(3): 34-38. Song Bo,Li Tongyu,Wang Weiqiang,et al.Transient numerical simulation of severe slugging in marine riser system[J].Journal of Liaoning Shihua University,2016, 36(3): 34-38.
[9] 谭先吉,杨涛,冯月晖,等.基于有限元的悬臂梁式压电换能器的模型辨识[J].系统仿真学报,2011,23(1):44-48. Tan Xianji, Yang Tao, Feng Yuehui,et al. Cantilever piezoelectric transducer moldel identification based on finite element analysis[J]. Journal of System Simulation, 2011, 23(1): 44-48.
[10] 刘阔,刘春时,林剑峰,等.VMC0540d机床床身和立柱结构的谐响应分析[J].机械设计与制造,2011,12:162-164. Liu Kuo, Liu Chunshi,Lin Jianfeng,et al.Harmonic response analysis for bed and column of VMC0540d machine tool [J]. Mechanical Design and Manufacturing, 2011,12:162-164.
[11] 吴晓金,王家序,肖科,等.水润滑轴承的动态仿真分析[J].系统仿真学报,2009,21(13):4167-4170. Wu Xiaojin, Wang Jiaxu,Xiao Ke,et al. Dynamic simulation of water lubricated bearing [J]. Journal of System Simulation, 2009, 21(13): 4167-4170.
[12] 翟廷科,刘雪东,刘文明,等.往复式压缩机出口管道振动分析及消振措施[J].化工机械,2010,37(2):214-218. Zhai Tingke, Liu Xuedong, Liu Wenming, et al. Vibration analysis and vibration elimination measures of the outlet pipe of a reciprocating compressor [J]. Chemical Engineeing & Machinery, 2010,37(2):214-218.
(编辑 王亚新)
Vibration Analysis of Compressor Piping System Based on Modal and Harmonic Response Analysis
Chen Jingchun1, Zhang Li1, Du Shengmin2, Sun Tie1, Zhang Suxiang1
(1.SchoolofMechanicalEngineering,LiaoningShihuaUniversity,FushunLiaoning113001,China;2.PetroChinaFushunPetrochemicalCompanyNo.3Refinery,FushunLiaoning113001,China)
Reciprocating compressor is one of the important equipments in the industrial field. The vibration problem has always existed in the pipe system of reciprocating compressor. By modal and harmonic response analysis, we can get the result that can accurately figure out the vibration characteristics of the structure. Aiming at vibration problems of reciprocating compressor piping of natural gas on the platformi n an oil field, it was found that the natural frequency of the piping was coincident with the resonance region of the excitation frequency by means of modal analysis and harmonic analysis. The method was proposed to change the supporting position and add reasonable support. Through numerical simulation and experiment data, it was found that pipe inherent frequency value was increased effectively, the amplitude of vibration was reduced, and the feasibility of the method was so verified.
Pipe system vibration; Natural frequency;Mode; Harmonic response
1006-396X(2017)03-0095-06
2016-11-17
2017-03-09
中国石油化工股份有限公司科技公关项目(311084)。
陈景春(1991-),男,硕士研究生,从事新型高效石化装备研究与开发;E-mail:chen_jingchun_yl@163.com。
孙铁(1964-),男,硕士,教授,从事新型高效石化装备研究与开发;E-mail:15141366088@139.com。
TH113.1;TH457
A
10.3969/j.issn.1006-396X.2017.03.017
投稿网址:http://journal.lnpu.edu.cn

