复习追问中的分类讨论思想渗透——以相似三角形复习课为例

沈顺良，张莲

（浙江省海盐县研训中心；浙江省嘉善县姚庄中心学校）

复习追问中的分类讨论思想渗透
——以相似三角形复习课为例

沈顺良，张莲

（浙江省海盐县研训中心；浙江省嘉善县姚庄中心学校）

渗透数学思想是复习课教学的一个重要目标，追问是常见的教学手段.在复习课教学中，通过追问能有效渗透数学思想.相似三角形复习中包含着丰富的分类讨论思想，通过情境问题的引导追问、开放问题的探究追问、典型错题的辩析追问、综合问题的交流追问等方式，能较自然地渗透分类讨论思想.

复习追问；分类讨论；思想渗透

章节复习课的学习目标：一是将学习的各知识点加以整理形成结构体系；二是能综合运用知识分析、解决问题，并渗透数学思想.相似三角形是浙教版教材九年级上册第四章的内容，本节相似三角形复习课的主要内容是复习相似三角形的判定和性质的运用，其中蕴涵了较为丰富的分类讨论思想.因此，本节课要求通过复习能将相似的不同判定和性质等知识形成网络，在具体问题中分析运用，并在知识整理和运用中渗透分类讨论思想.追问是课堂教学的重要手段，通过复习追问能够较好地渗透分类讨论等数学思想.

一、情境问题的应答追问中整理知识并隐含分类讨论

例1如图1，点D是射线AO延长线上的一个动点，试添加一个条件，使得△ABO和△CDO相似，并说明理由.

生1：添加的条件是∠B=∠D.

师：你的理由是什么？

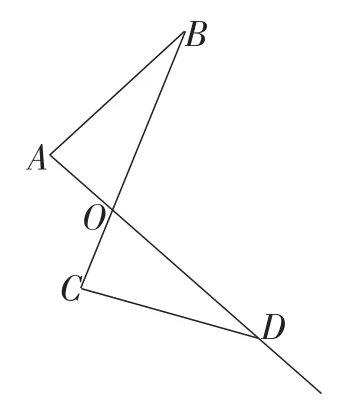
图1

生1：两角对应相等的两个三角形相似.

教师板书.

生2：我添加的条件是，理由是两边对应成比例，且夹角相等的两个三角形相似.

教师板书.

生3：我添加的条件是AB∥CD，那样能得到∠B=∠C，∠A=∠D，其实理由和生1是一样的.

生4：，我的理由是三边对应成比例的两个三角形相似.

教师板书.

师：前面4位同学都呈现了正确的条件添加，在一定条件下要判定两个三角形相似，该如何去选择判定的方法呢？

生5：应该根据条件从三角形的元素，即分别从三角形的角、边、边角混合的角度来考虑，即需要依据已知三角形元素之间的关系的条件，分别选择两角相等、两边成比例且夹角相等、三边成比例来证明.

师：这里具体是如何分类选择的？

生5：是按照角（边）数来分类选择，分别有两角（三角）对应相等、一角对应相等（加两夹边对应成比例）、零角（加三边对应成比例）共三种判定方法.

师：那相似三角形的性质又有哪些呢？

生6：好像是有四条性质吧.

师：你能否将它们做个梳理？

生6：从三角形的相关量，即角、边、周长、面积等来考虑，有相似三角形的角对应相等、相似三角形的边对应成比例、相似三角形的周长之比等于相似比、相似三角形的面积之比等于相似比的平方.

师：这样通过梳理我们得到了关于三角形基本元素角（边）的三个判定定理和关于三角形量的四个性质定理.

【点评】复习课的重要目标是按照知识方法的联系形成知识网络，学生对情境问题的不同回答，教师在应答中追问在一定条件下如何选择判定三角形相似的方法，使学生感受到需要梳理分类，接着教师追问了依据和思考角度，引导学生将三个判定定理从三角形的基本元素，即角的个数（边的条数）来分类；同样教师追问相似三角形性质的梳理，引导学生从刻画三角形的量，即角、边、周长、面积等角度来思考.这样较好地将各个判定定理和性质定理相互联系，形成了相似三角形判定和性质的知识网络，又通过运用三角形判定和性质时不同选择梳理的追问，自然隐含了根据组成三角形基本元素角（边）、刻画三角形的量（角、边、周长、面积等）的分类途径.

二、开放问题的探究追问中引导分类讨论

例2如图2，在△ABC中，AB＞AC，D是线段AB边上的点（不与点A，B重合），过点D作直线DE交AC于点E，使截得的△ADE与△ABC相似.你能画出符合条件的直线吗？

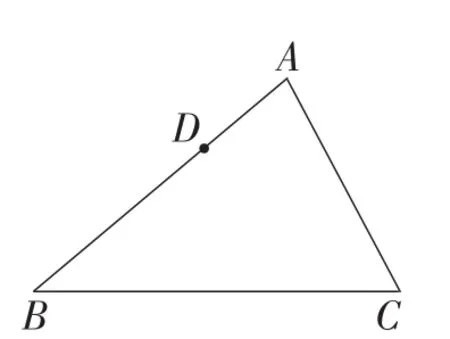
图2

生7：作DE∥BC，这样∠ADE=∠B.

生8：一定是这么画的吗？

师：你为什么有这样的疑问？

生8：要使△ADE与△ABC相似，现在只有∠A是对应确定的，而其他两个条件无论是另两对对应角还是夹角的对应边，对应关系都还不确定.

师：对应关系不确定时，你认为该如何让它能确定呢？

生8：需要按角或边的对应来分类确定.这里我还可以画出另一条，只要使得∠ADE=∠C即可，所以有两种对应的情况，如图3所示.

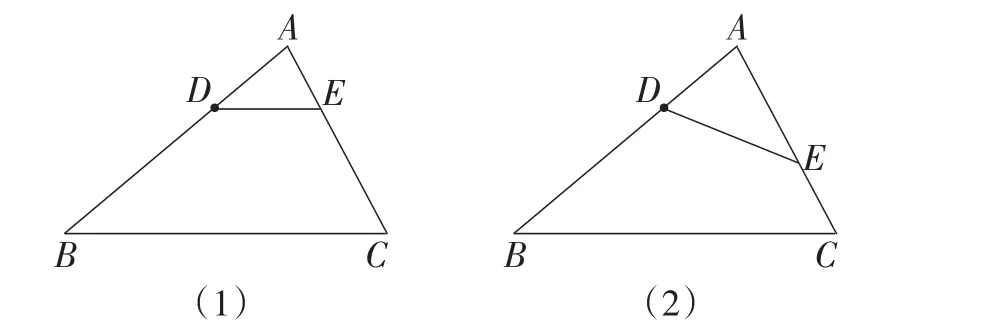
图3

师：这就是分类讨论，其分类标准为判定定理中的角或边.

变式：如图4，在△ABC中，已知∠ADE=∠ACB.

（1）△ADE∽△ACB？

（2）连接DC和BE交于点O，你还能找到其他的相似三角形吗？

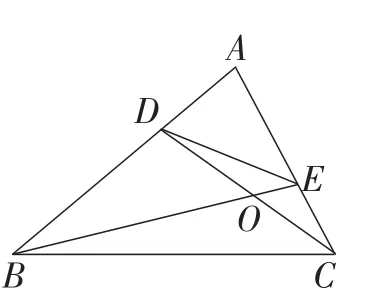
图4

生9：△ADE∽△ACB是成立的，还能得到△ABE∽△ACD.

师：你是怎么思考的？

生9：判定三角形相似可以从对应角相等组数来分类，即两角相等，一角相等且两夹边对应成比例，三边对应成比例，从两组角来看得到△ADE∽△ACB，从一组角来看得到△ABE∽△ACD.

师：你具体是怎么得到△ABE∽△ACD的？

生9：由△ADE∽△ACB，可得到.而∠A=∠A，得到△ABE∽△ACD.

师：生9既能从判定三角形相似中按角分类得到不同的结论，又能通过△ADE∽△ACB的性质运用来得到，还有其他的相似三角形吗？

生10：△DOB∽△EOC.

师：你又是如何想到的？

生10：从条件的运用即性质来看，除了得到对应边成比例，还能得到角的相等，即∠ABE=∠ACD.再根据对顶角∠DOB=∠EOC，得到△DOB∽△EOC.

生11：由对顶角还有∠DOE=∠BOC，然后思考有没有对应边成比例，发现了从△DOB∽△EOC中可以得到，所以得到△DOE∽△BOC.

师：运用条件△ADE∽△ACB从边和角分类得到两种途径，然后又从两类对顶角相等条件的运用来思考，从而自然探究得到了结论.

【点评】分类讨论中重点是把握何时需要分类、对谁分类和怎么分类，上述教学过程正是教师在学生探究后的交流中加以分类讨论的引导追问.例2解决中是因为对应关系不能确定所以需要分类，要让对应关系能确定，所以按对应边分类或是按对应角分类，变式的解决中涉及相似三角形判定和相似三角形性质运用的不同途径，它们都是关于角（边）来分类思考的.因此，教师首先是根据∠A相等条件下的不同判定方法进行追问，然后对得到结论△ADE∽△ACB的不同运用追问性质的运用，强化了关于角（边）的分类讨论.

三、典型错题的错因辨析追问中凸显分类讨论

例3已知△ABC的三边分别是2，3，4，△DEF的一条边是12，若△DEF和△ABC相似，则△DEF另两边的长分别是多少？

图5

师：实物投影仪展示如图5所示，有什么问题吗？生12：此题中两个三角形相似的边角对应关系不能确定，那就需要通过讨论边或角的对应来确定，所以还应该有其他两种情况：（1），解得x=8，y=16；（2），解得x=6，y=9.故另两边长为8和16，6和9，18和24.

师：此题的订正你有什么感受？

生12：运用三角形相似性质时，若对应关系不确定，则必须要按角或边分类讨论来确定.

例4如图6，在△ABC中，点D，E分别在边AB，AC上，连接DE，CD，有∠1=∠2=∠3.写出其中的所有相似三角形，并说明理由.

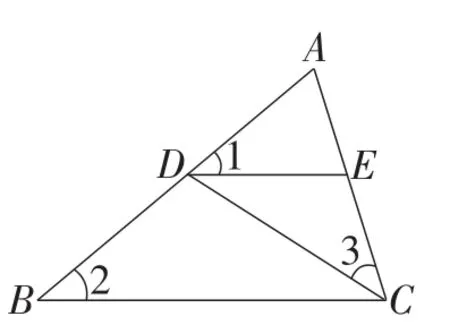
图6

生13：（实物投影仪展示图7）根据前面两类基本图形得到两对相似三角形.

图7

生14：还没有找全，另外还有，△ACD∽△ABC.

师：分析一下生13为什么会没有找全，你又是如何找到的？

生14：生13可能是只考虑了条件∠1=∠2=∠3中的∠1=∠2，∠3=∠2的运用，并且条件∠3=∠2中两角对应的三角形除了△ACD∽△ABC，还有△DEC∽△CDB，另外还漏掉了考虑∠1=∠3对应的△ADE∽△ACD.

师：从例4的订正中，你对分类有什么感受？

生14：判定三角形相似时，既要分析题中已知角或边的关系能否确定对应，又要考虑判定时选用边或角的途径选择.

师：正是为了确定，所以一是从三个角相等条件的运用看需要分两类；二是从每种情形的两角相等所对应三角形相似角度来分类找，这样就能既不重复又不遗漏.

【点评】从反例的角度让学生经历发现问题的过程，从而也经历了发现需要分类和怎么分类的过程.一方面，通过例3中追问分析发现错误的原因，强调了对应角（边）不确定时需要分类，充分体验了分类讨论的必要性，并能自然分类；另一方面，通过例4也让学生体会到分类讨论的对象要明确，分类讨论必须按照同样的标准（角或边），以及不重复、不遗漏等.

四、综合问题的交流追问中渗透分类讨论

例5有一块直角三角形废牛皮料，两直角边长为AB=20 cm，AC=15 cm，现要裁剪出一个最大面积的长方形（使得长方形的一边落在三角形的一边上），问采用什么样的方案比较合适，其最大面积是多少？

小组合作讨论.

生15：（实物投影）应该是有如图8、图9两种方案，即长方形一边分别落在斜边BC上、落在直角边AB （AC）上.需要分别求出两种方案下的最大值，再比较它们中的较大值即为所求.

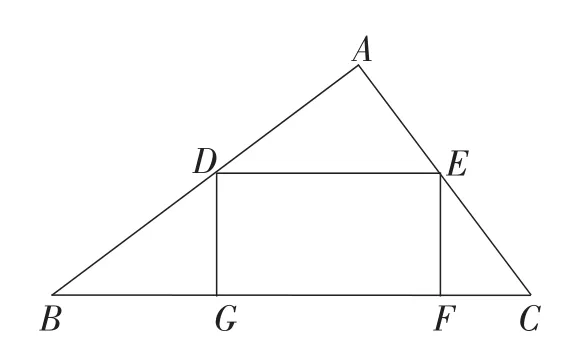
图8

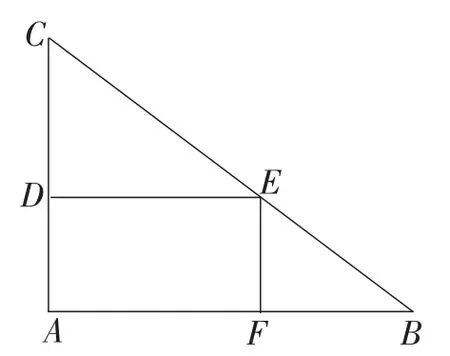
图9

师：本来图形是不定的，两种方案是怎么想到的？

生15：要解决此题首先要画出图形，即长方形放置方案对应图，按照题中的要求，要裁剪出一个最大面积的长方形，并且长方形的一边落在三角形的一边上，要考虑长方形一边分别落在AB，AC，BC上，其中前两类都为如图9所示的方案.

师：具体是怎么求的？

生15：在第一方案中，如图10，作AH⊥BC，交BC于点H，交DE于点I，BC=25 cm.由等积法，得AH==12 cm.设DG为x，由△ADE∽△ABC，得.得DE=，S矩形DGFE= DE·DG=() 12-x x.由二次函数求最值得当x=6 cm时，S最大=75 cm2.

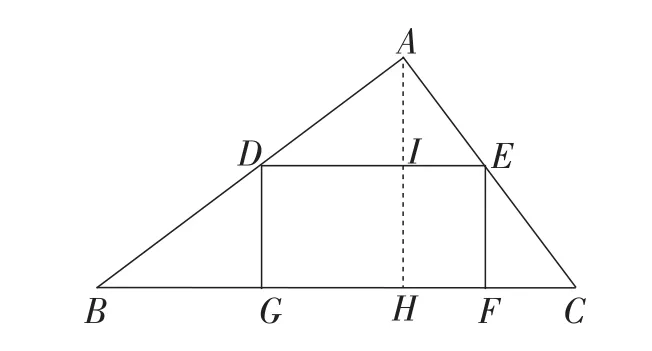
图10

生16：我们组设的是长方形的另一边长，即设DE=x，最后结果也是一样的.

师：第二类方案如何解决呢？

生17：类似于第一类方案的解决，其中也有两种不同的设变量法，求得的最值也是75 cm2.

师：所以所求结果即为75 cm2，请你回顾此题解决中的分类.

生17：此最值问题的分析中首先要确定长方形的一边位置，按它所在三角形边有两类不同的方案，而每类方案的代数化中又有两类不同的设元法，它们都是将实际问题数学化，几何问题代数化.

师：上述不同方案和不同设元的分类中，都是按照直角三角形的边和矩形的边来分类的.

【点评】方案要确定，则需要对长方形一边落在三角形的哪一边上进行分类讨论，然后转化为几何语言，再将长方形两边长的依赖关系中设其中一边长进行分类，最后是将所求得的不同类下的最大值进行比较，分类讨论贯穿了综合问题的分析、交流和解决过程中，后面的分类、回顾、追问，引导学生清晰矩形一边落在三角形哪条边上，矩形面积数学化时设哪条边都是以边来分类讨论的，突出了分类标准的确定.

本节课中，教师引导学生复习整理知识是明线，在较复杂问题的分析中，将其通过分类增加所需条件分情况讨论，进行适时的追问，让学生体会条件不充分或条件不确定时分类的作用，渗透了分类讨论思想这条暗线，能够在复习课中让学生对知识结构更加清晰，又能积累数学思想的运用.

［1］中华人民共和国教育部制定.义务教育数学课程标准（2011年版）［M］.北京：北京师范大学出版社，2012.

［2］教育部基础教育课程教材专家工作委员会.《义务教育数学课程标准（2011年版）》解读［M］.北京：北京师范大学出版社，2012.

［3］黄智华.数学教学应关注学生思维能力的培养［J］.中国数学教育（初中版），2014（1/2）：34-36.

2017—03—18

沈顺良（1965—），男，中学高级教师，浙江省优秀教研员，主要从事数学教育与中学数学研究．