整体设计教学发展核心素养——用类比的方法研究新函数

王万丰

（浙江省台州市路桥实验中学）

整体设计教学发展核心素养
——用类比的方法研究新函数

王万丰

（浙江省台州市路桥实验中学）

《义务教育数学课程标准（2011年版）》在“教学建议”中指出：数学活动经验的积累是提高学生数学素养的重要标志.函数是数学核心内容，初中阶段学生通过研究一次函数、二次函数、反比例函数，已具备了研究函数的活动经验.用类比的方法研究新函数，引导学生从整体的视角规划研究函数的思路与方法，设计有效的探究活动，使学生经历数学的发展过程，发展学生的数学核心素养.

整体设计；新函数；核心素养

2016年4月，笔者开设了一节区级中考专题复习的公开课，此时九年级学生已经开始中考复习.在初中阶段，学生已经经历了学习一次函数的陌生到研究二次函数的历练，再到研究反比例函数的熟练，应该说学生已经具备了规划研究函数的思路与方法，所以笔者构思了一堂“用类比的方法研究新函数”的公开课.

一、课前思考

1.函数知识的整体性与内在联系

在初中阶段，函数知识的学习包括一次函数、二次函数、反比例函数，并且在学习的过程中都要学习函数的概念、函数的三种表示方法、描点法画出函数的图象，以及结合函数图象研究函数的性质和应用等内容.具体如表1所示.

表1

2.一次函数、二次函数和反比例函数的基本学习过程

函数图象与性质是函数知识的主体，通过对函数图象与性质的学习，从数量和图象两个侧面，以及相互联系中，显示出函数的本质特征是联系变化，这是学习的主线.

通过函数的研究历程可以概括出研究函数的基本过程，在研究函数的性质的过程中，通过观察发现图象的规律，再根据这些规律得出关于数值大小的性质.一般来说，从函数的性质来看，研究函数的性质主要研究其图象分布规律，以及对称性、增减性及特殊点.归纳如图1所示.

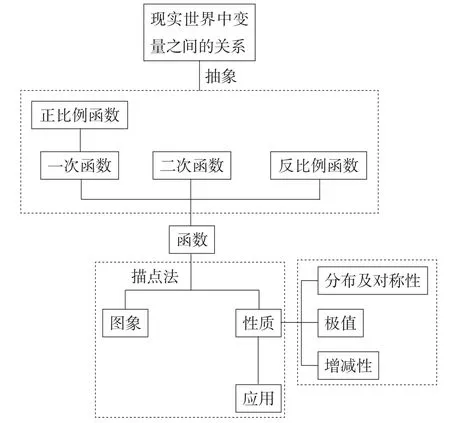
图1

基于以上归纳与思考，笔者以为，对于学生的数学能力和数学素养，不能仅仅从“会做数学”的角度进行评价，更应该从学生有没有“会学数学”的能力和素养进行评价，其中一个方面的体现就是学生能否总结出知识的内在联系、脉络、结构，形成整体的理解，同时又能理解哪些地方是关键，学会能把书从薄读到厚，又能把书从厚读到薄.

二、教学分析及流程

1.教学分析

教学目标：

2.教学流程

环节1：创设情境，形成概念.

问题1：分别写出下列函数解析式.

（1）某种小轿车的购车费用为10万元，每年应缴保险费等各类费用共计0.4万元，n年的保养、维护费用总和为(0.1n2+0.1n)万元.设年平均费用为w（元/年），

（2）已知某汽车的依次运输成本包含以下三个部分：一是固定费用，共360元；二是燃油费，每千米1.6元；三是折旧费，它与路程的平方成正比，比例系数为0.001.设汽车一次运输路程为x千米，设平均运输成本为y（元/千米），求y与x的函数关系式.

（3）某民办学校每天的支出总费用包含以下三个部分：一是教职工工资4900元；二是学生生活费成本每人10元；三是其他费用.其中，其他费用与学生人数的平方成正比，比例系数为0.01.设该校有学生x人，该校每天学生人均投入为w元，求w与x的函数关系式（生均投入=支出总费用÷学生人数）.

追问：试归纳这三个函数的特征，并对此类函数下定义.

环节2：回顾方法，展望思路.

问题2：回顾我们研究函数的方法，思考如何研究新函数？

通过与研究函数思想方法类比，师生共同得出如下策略：（1）研究的内容主要是研究函数的图象、性质及应用；（2）运用特例研究可先设a=1，b=1，c= 0，再归纳一般性；（3）通过描点法画函数y=x+的图象.学生独立完成绘制函数图象，并尝试说出函数y=x+的性质.

追问2：从哪几个方面来说出函数的性质？

归纳得出几个方面：（1）图象的分布及对称性；（2）极值或特殊点；（3）增减性.适时完善图1，学生得出函数y=x+的性质.

环节3：逻辑推理，得出性质.

阅读材料：用配方法求最值.

已知x，y为非负实数，

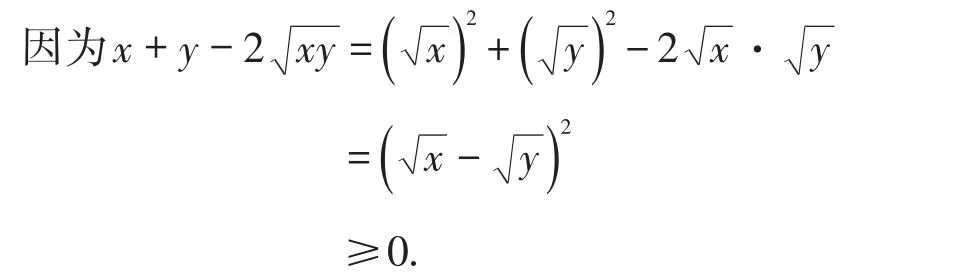
环节5：回归应用，解决问题.

问题4：结合探究的性质，解决下列问题.

对于问题1可设计如下问题串.

（1）这种小轿车使用多少年报废最合算（即使用多少年的年平均费用最少）？最少年平均费用为多少？

（2）求当x为多少时，该汽车平均每千米的运输成本最低？最低是多少？

（3）当学校学生人数为多少时，该校每天生均投入最低？最低费用是多少？

三、整体设计教学，用数学发展学生数学素养

1.类比思想——建立知识系统之间关联的纽带

数学知识系统之间往往是关联的，数学材料的逻辑组织化，不仅仅停留在不同的局部内容的逻辑组织上，还需要通过逻辑构建，建立不同的局部知识系统之间的关联，把已经建立的知识系统及其学习经验应用于新的内容的学习中，类比是建立类似的知识系统之间的关联的纽带.

当前教学中仍存在的几个问题，如教师教学就事论事，对学科课程整体理解不够，导致学生以知识获取为主，对学科核心思想思考不够；教师对课时教学改进多，对单元整体性设计不够，导致学生获取知识再现为主，关注迁移解决新问题不够.《义务教育课程标准（2011年版）》在“教学建议”中也指出：数学活动经验的积累是提高学生核心素养的重要标志.

本节课中，通过回顾整理一次函数、二次函数、反比例函数的研究历程，发现研究函数过程的共性，发现研究函数性质的共性，进而类比得出研究函数的思路与方法，通过类比旧知识的活动经验，得出研究新函数的思路与方法，整个过程，运用类比思想，学生完全自主构建，教师做引导者和合作者.

2.“抽象、推理和模型”是数学的核心素养

数学的核心素养，必须体现数学学科的本质，体现数学学科本质的无疑是数学的基本思想——抽象、推理和模型，这三种基本思想涵盖了数学的产生与发展.另外，数学的三大特征——高度的抽象性、逻辑的严谨性和广泛的应用性，三种基本数学思想与数学的三大特征高度对应.因而三大基本数学思想在数学发展历程中起着关键的核心作用，在教学中应时刻关注这三大核心数学素养的发展.

在本节课的教学中，通过实际问题抽象出新函数的共同特征，从而对其下定义，形成概念，发展学生的抽象思维能力；在研究函数性质的过程中，不仅通过观察归纳得出函数的性质，发展学生的几何直观能力，特别是在个别性质的得出中，仍然需要通过逻辑推理，发展学生的推理能力，而这种数学推理承载着其他学科没有的素养；通过对实际问题中函数类型的抽象，建立起新的函数模型，进而研究新函数的性质并应用于实际，解决实际问题中的最值问题，体现了函数的模型思想.

3.构建知识网络，整体设计教学

在整体教学、系统逻辑构建的教学思想下，先引导学生立足整体内容提出问题，规划研究的思路和方法，制定研究计划，然后，完成研究内容.在这种整体逻辑构建的教学设计中，是先有整体视野，聚焦数学观念和思想方法，再根据需要对各种子问题进行研究，可以给学生宏观的数学视野，在见森林的基础上再见树木，这符合大脑信息加工的从整体到部分、从粗略到精细、从定性到定量的规律.

从教学过程来看，整体把握知识之间的内在联系，构建知识网络，不仅能深化对每个部分的理解和应用，而且能从中提炼出数学思想，这样的学习方式，不仅有助于掌握知识、技能和方法，提升学习效率，而且加深了数学中通性、通法的认识，提升学生学习和研究数学的水平，提升数学思维的能力.同时，也是发展学生核心素养的必要举措.

［1］中华人民共和国教育部制定.义务教育数学课程标准（2011年版）［M］.北京：北京师范大学出版社，2012.

［2］教育部基础教育课程教材专家工作委员会.《义务教育数学课程标准（2011年版）》解读［M］.北京：北京师范大学出版社，2012.

［3］吴增生.用数学发展思维：基于脑、适于脑、发展脑的数学教学策略［M］.南昌：江西教育出版社，2016.

［4］王亮亮.中考数学改革对初中数学教学的反拨作用［J］.数学通报，2016（5）：10-14.

［5］陈林香.顺应认知整体架构：人教版“平方根”教学的改进尝试［J］.中学数学教学参考（中旬），2016（9）：18-21.

2017—03—15

王万丰（1979—），男，中学一级教师，主要从事初中数学教材及教学研究.