万变不离其宗
——有关含字母的一元一次不等式（组）的综合应用的变式探究

2017-06-20 09:43北京师范大学附属中学

卫星电视与宽带多媒体 2017年8期

北京师范大学附属中学杨维

因为解一元一次方程和解一元一次不等式的步骤非常类似，在学完解一元一次方程以后学生再学习解一元一次不等式会很快入手。而解二元一次方程组和一元一次不等式组却存在较大差异，主要差在最后解（解集）的寻找过程中，二元一次方程组只需要用大括号连接求出的两个未知数的值，而不等式组的解集学生凭空却不太容易写出来，需要通过画数轴找出不等式组的解集。这也说明在解不等式尤其是不等式组中画数轴很重要，而当不等式（组）中含字母时，画数轴更加重要，既要会画数轴，还要会用数轴来确定不等式（组）中字母的范围，可谓真正做到数形结合。本文结合自己做的一节研究课——有关含字母的一元一次不等式（组）的综合应用，在这节课中进行的变式探究，与同行交流。

一、引入

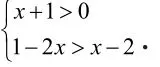
我以大家熟悉的比较常规的一元一次不等式组引入，让大家重温解一元一次不等式组的步骤：分别解两个一元一次不等式，在数轴上表示出解集，结合数轴确定最后不等式组的解集。有的学生可能也可以不画数轴直接得出最后的正确答案。

二、变式

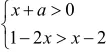
将不等式组（1）中的不等式中的常数1换作字母a，当然题目由解不等式组变成在不等式组有解的情况下求a的取值范围。如果题1中画数轴还不那么突出和重要的话，变式1中数轴是解题的重要工具，是不画不行了。初步凸显了数轴在解含字母的不等式组中的重要性。

解法：

第一步：像题1一样分别解出不等式组中的两个不等式的解集，第二个不等式的解集是确定的：x〈1，第一个不等式的解集不确定：x〉-a；

第二步：画数轴，首先画x〈1对应的解集，结合题意不等式组有解，说明两个解集有公共部分，确定-a的大致位置，在1的左侧；

第三步：通过试验，让-a和1相等确定界点可否取到，从而确定-a的具体范围，进一步得到a的取值范围。

三、提升

2. 已知关于x的不等式2x-b〈0的正整数解恰是1, 2, 3, 则b的取值范围是 _______.

这是一个含字母的一元一次不等式，给了正整数解，要确定字母b的取值范围。在变式1的基础上，稍微有点提升，好多学生可能只会想到b有下限，实则还需要确定字母b的上限。应该说有点难度。但是画了数轴后，学生就会豁然开朗了。

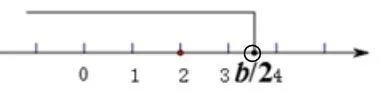
如上图，先画出数轴标出1，2，3，完成解题第一步；根据题意，解集中恰好仅包含1，2，3这三个正整数解，确定在3右侧，好多学生在这会丢掉b的上限，因为题目中有个“恰”字，说明只能到3，而不能包含4，这样进一步确定在4左侧，也就是说在3和4之间，完成解题的第二步；第三步，确定是否包含临界点（3和4），可以通过带进去试的方法，最后确定的具体范围，从而求出b的范围。

四、综合

此题在第2题的基础上又有了提升，不等式变为不等式组，字母个数由一个变为两个，当然条件由正整数解恰为1，2，3变为整数解只有1,2, 3。题目形式上有了变化，看似变难了。但如果掌握了前面画数轴的办法，本质上又没有变。

不等式②中b的范围的确定和刚才题2完全一样，不等式①中a的范围的求法和②中b的范围的求法完全一样，区别在于在界点的确定上。所以有了解第2题的基础，解第3题就轻而易举了。

五、变式

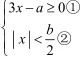
此题在题3的基础上，又有了变化。将题3中的不等式②变成了绝对值不等式，看似变得更难。但结合绝对值的几何意义，还是通过数轴画出图形后，本质上基本没有变。解法和刚才一样。

解法：第一步：由不等式②得到，由不等式①得到

第二步：画数轴，同样先在数轴上标出已经确定的1，2，3，然后让在数轴上动起来，但要注意与是关于原点对称的，这样就容易确定在3和4之间，对应的-一定会在-4和-3之间，所以下限必须由来控制，也就是说，在0和1之间，不等式组的解集是

数轴如下图所示：

第三步：确定是否包含界点，从而最后确定a,b的范围。

在变式2的基础上条件有了变化，如果掌握了如何通过画数轴来确定待定字母在数轴上的位置，这道题也就手到擒来了。

在变式2的基础上，我们知道在2和3之间，此时-一定会在-3和-2之间，也就是说原不等式组的解集一定是而不再是换言之，此时应该在-的左侧。其实在画数轴的时候也很容易发现-2，-1和1, 2是关于原点对称的，也是关于原点对称的，如果上限由确定，那么下限一定由-来控制。

数轴如下图所示：

结合数轴可以更直观地看出变式2和变式3之间的关系，也可以直接看出不等式组中解集之间的关系。

综合所述，有关含字母的一元一次不等式（组）的综合应用的题目虽千变万化，不胜枚数，但解这类题有通法：

1. 求不等式(组)的解集；

2. 根据题意,把不等式(组)的解集表示在数轴上；

3. 利用数轴,确定有关字母的取值范围；

4. 确定是否包含边界点；

5. 确定结论。