一元方程定理
广西建工集团第四建筑工程有限责任公司南宁分公司 蒙 醒
早在3600年前,古埃及人写在草纸上的数学问题中,就涉及到了方程。公元825年左右,中亚细亚的数学家阿尔·花拉子密曾写过一本名叫《对消与还原》的书,重点讨论方程的解法。在本文构造的方程中,用传统的方法求解比较麻烦,用作者提出的定理求解则较为简捷。
一、一元方程求根法1
1.求方程的解
解:
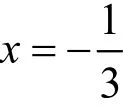
经检验是方程的解
2.求方程的解
解:
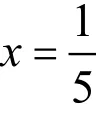
经检验是方程的解
经过观察,在中,用y,a,b,c,d代替方程中的已知数,得到,又的解分别为和,则有的解为。
已知a,c为常数且不全为0;b,d为常数且不全为0,ad≠bc,y是常数。
求证:的解为
证明
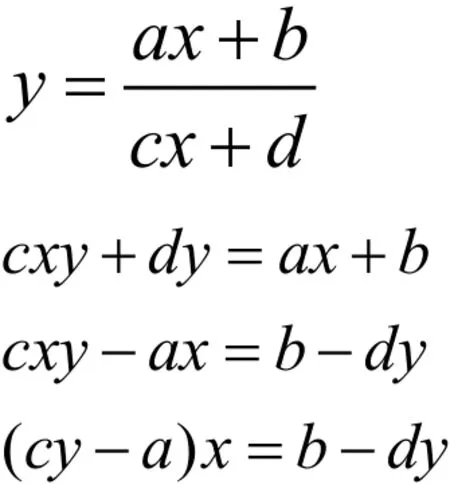
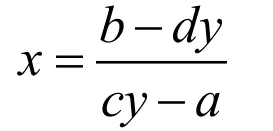
∴得证
得到
方法1
的解为
都 是ax,b,cx,d的特例,缺少的一项或两项,缺少的项中a,b,c,d,为0,所以缺少的项为0,为了计算简便,在本文中忽略不计。
用方法1求两个特例的解。
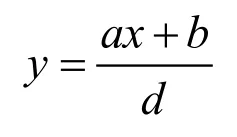
方法1
的解为
证明
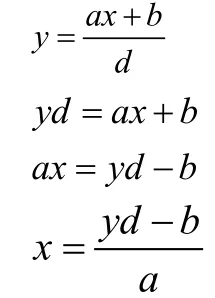
在中,当d=1时,可以写成
方法1
的解为
证明
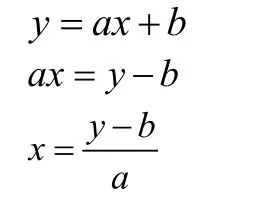
因为与方法1求出的解与证明得出的结果一致
所以方法1在解及y=ax+b中适用
其它特例可参照上文。
二、一元方程求根法2
a,c为常数且不全为0;b,d为常数且不全为0。adbc≠qh代替的数是除0以外的常数。y和 qi代替的数为常数。(q是h,i的序号。 qhqi分别代替一个数,p是q最大的数)
在的基础上乘以一个数或除以一个数、加上一个数或减去一个数混合起来可得到
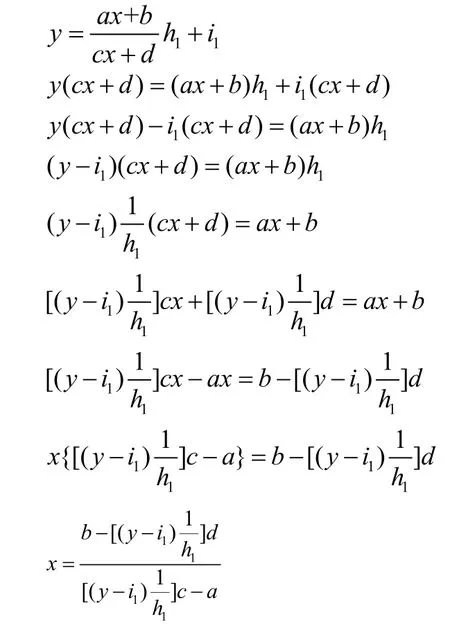
在的基础上乘以一个数或除以一个数、加上一个数或减去一个数混合起来可得到
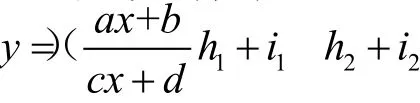
易得
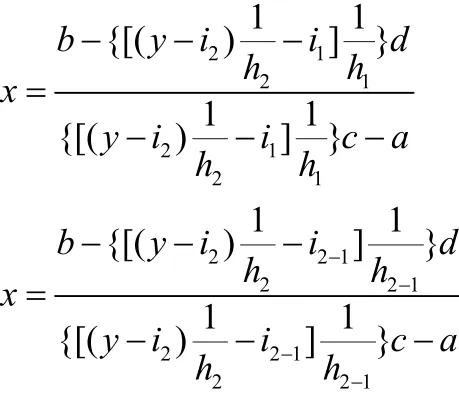
在的基础上乘以一个数或除以一个数、加上一个数或减去一个数混合起来可得到
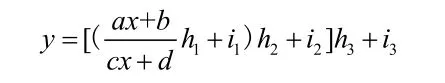
易得
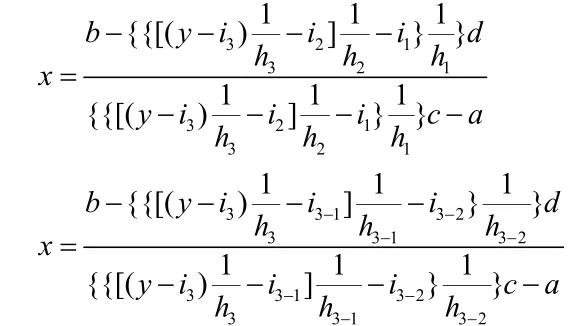
在的基础上乘以一个数或除以一个数、加上一个数或减去一个数混合起来可得到
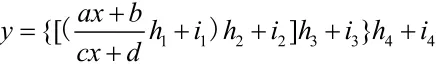
易得
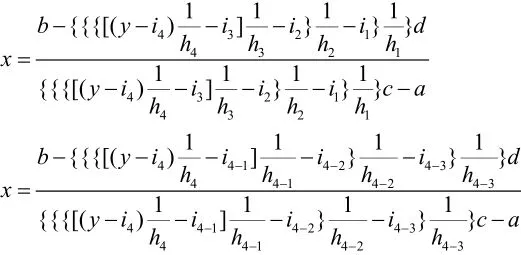
由上述可以看出以上是
的解为的结论
所以当hq,iq中最大的数q=4时,得到
推论 方法2
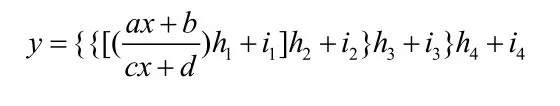
的解为
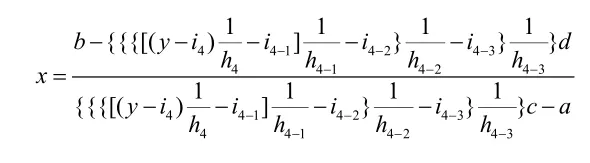
我将上述方程中的一组 iq,hq称为一组常数项,当最大的数q即p=2,3,4时,x的解中 iq, hq从左边第二组起最大的数q即p依次递减1,直至相减后iq,hq的序号q都等于1
特例可参照上文。
三、一元方程定理
在的基础上乘以一个数或除以一个数、加上一个数或减去一个数混合起来再无限循环得到
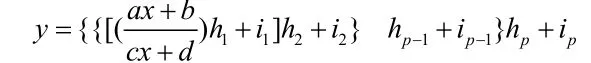
定理a,c为常数且不全为0;b,d为常数且不全为0。ad≠bc.hq代替的数是除0以外的常数,y和 iq代替的数为常数。p≥4。(q是h,i的序号。hq, iq分别代替一个数。p是q最大的数。)
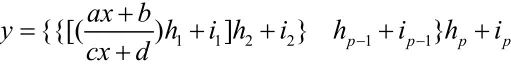
的解为
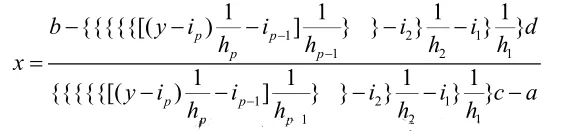
注 需检验的最后进行检验即可。
证明
当P=4时
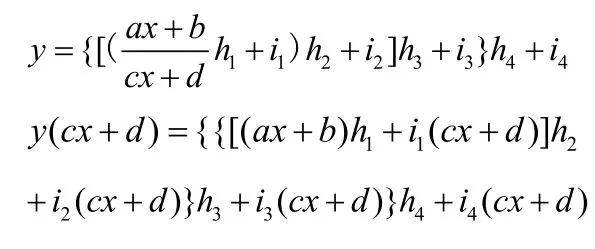
易得
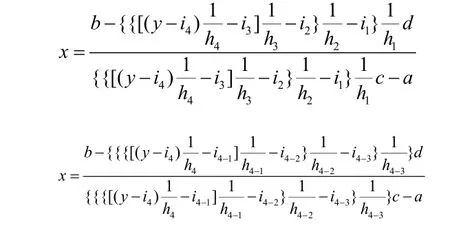
假设p=k(k≥4)时方程成立,即
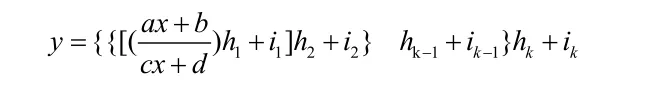
的解为
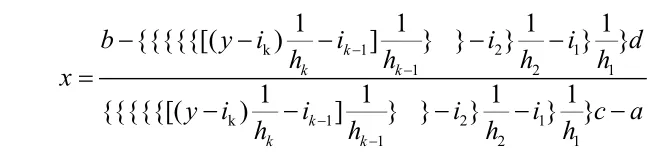
那么当p=k+1时,
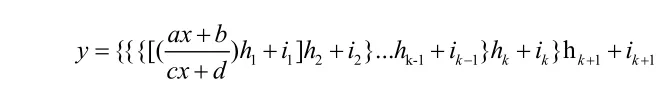
易得
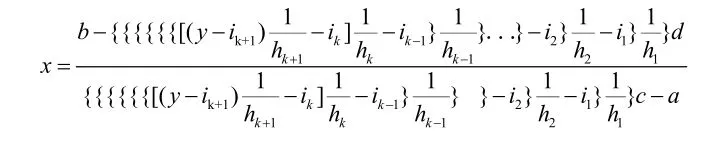
∴当p=k+1时方程成立
∴当p≥4时,定理成立

