一种基于FFT的快速高精度的频偏估计算法

蔡 青，陈海腾，徐 勇

（南京熊猫汉达科技有限公司，南京 210014）

一种基于FFT的快速高精度的频偏估计算法

蔡 青，陈海腾，徐 勇

（南京熊猫汉达科技有限公司，南京 210014）

在卫星通信系统中，低速率信号的传输和接收端的低信噪比会导致很大的频率偏移。针对这一问题，本文提出了一种基于快速傅里叶变换（FFT）的三谱线内插算法。

快速傅里叶变换FFT；频率估计；Quinn算法；Rife算法；克拉美-罗限

1 引言

由于卫星通信设备需要适应多种复杂度不同的通信环境，因此针对处于噪声污染环境中的接收端设备而言，快速获得高精度的频率参数估计便显得尤为重要。在卫星通信过程中，为了修正移动载体和卫星之间的相对运动而产生的多普勒频移，卫星通信设备通常采用载波同步技术对该频差予以补偿。基于锁相环跟踪的传统载波同步算法因收敛速率慢，捕获时间长，并且频偏估计精度容易受到信噪比的影响，其性能受到一定的限制[1]。近年来，基于FFT的载波频率估计插值算法，因其速度快、精度高、计算量小等优点，在深海探测、雷达、振动工程等领域也得到广泛的应用。

国内外学者对频域估计算法的研究提出了很多方法。例如：最大似然估计（Maximum Likelihood Estimation，ML）算法，当用ML算法对高斯白噪声估计载波信号频率，估计误差可以达到CRLB。因此，ML算法是一种最优估计，但其缺陷是信号搜索需非常大的计算量和时间；另一种算法则是将信号幅度谱的两根最大谱线进行插值估计频率的方法（Rife算法），其缺陷是当接近量化频点时估计误差相当大，而改进后的Rife算法仍然需要庞大的计算量；第三种是Quinn算法，即利用信号FFT主瓣内幅度次大谱线与最大谱线的FFT系数复数值之比的实部进行插值，其缺点是低信噪比条件下，当信号频率靠近DFT的量化频率时，估计误差较大。

上述算法都有各自优缺点，不能同时在获得高稳定性、高精度的同时兼具较低计算量，在实际应用场景中，通常需要快速的获得更高的精度。本文提出利用FFT的复数结果，将最大峰值频谱和相邻两侧一个量化频点的谱线进行插值算法，在仅比Rife和Quinn算法计算增量不多的情况下，获得更高的估计准确性和稳定性。

2 Triple_IN算法的原理

假设该检测信号为单频率的复正弦信号x(t)=A*exp[j(2πf0+θ) ]+z(t)，式中信号的振幅、频率和初始相位值分别为A、f0和θ。z(t)表示均值为零、方差为2σ2的高斯白噪声。若采样时长T=N⁄fs，频谱分辨率是∆f=1⁄T，其中fs是采样频率，N是待采样点数。采样序列为

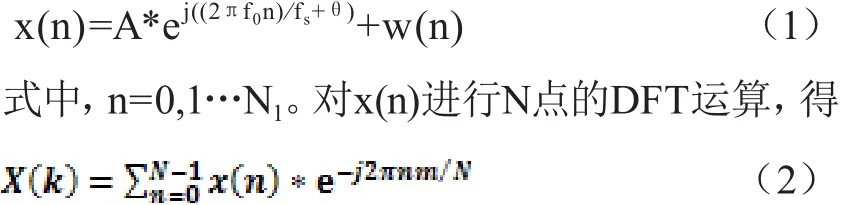
而δ为信号真实频率与频率粗估计值得差值相对∆f的倍数即估计误差精度，该值在[-0.5,0.5]的范围内。根据的最大幅度频谱的|X(k) |所对应频率索引m'，残余频偏δ，则估计位置m0=m'+δ，所以实际估值频率为

现利用幅度谱S(k)=|X(k) |进行多项式频率插值以提高估计频率的精度，设二次多项式S(k)=Ak2+Bk+C近似于幅度谱的值，则k0及相邻量化频点位置为(k0-1,S(k0-1))，(k0,S(k0))， (k0+1,S(k0+1))，即得

此处要求估计位置m'必须在[1,N⁄2]范围内，估计精度范围δ∈[-0.5,0.5]。该算法的均方根误差（RMSE）在-5dB信噪比条件下达到CRLB的渐近线（Asymototic CRLB，ACRB）的1.1812倍，具备非常高的准确性和稳定性。

3 算法的仿真和性能分析

为了准确和可靠的评估各载波频率估计算法的性能，以高斯白噪声下的估计范围内，不同条件下的MATLAB中进行算法建模，每次进行10万次的蒙特卡洛仿真。根据公式（1）的载波信号，输入信噪比SNR=A2/2σ2，设置参数：初始相位θ设为固定π⁄3，fs为5e3赫兹，N值为1024，且设定初始频率f0=((212+δ)*fs) ⁄N，δ为[-0.5,0.5]内步进为0.025的共41个离散频率值。当N》1时，频率无偏估计值的最低方差下限CRLB可以近似为ACRB为

本文根据频率估值归一化频率的R MSE与RMSE{ACRB}的对比来衡量综合算法估计值的精确性。

3.1 估计性能分析

Triple_IN算法的应用必须符合奈奎斯特采样定理，即2f0≤fs。假设采样频率fs=1⁄T，则频率估计范围即f0≤|fs⁄2|。如图1可知，在δ的变化范围内，SNR在{-8dB，-5dB，0dB，5dB}条件下反映本算法归一化频率估计性能的稳定性。

如图1所示，在残余频偏δ的变化范围内，估值性能趋于稳定，而伴随信噪比的陡降，当SNR=-8dB时，在0.45≤|δ|≤0.5时仍逼近ACRB的1.2898倍，说明其稳定性不受信噪比影响。在[-10dB, 10dB]范围内，|δ|取{0，0.05，0.15，0.25，0.35，0.45}条件下，进一步观察该算法可靠性。

如图2所示，随着信噪比的增大，估值频率的RMSE越趋于ACRB曲线，而随着信噪比的降低，|δ|越大越偏离ACRB。但即使在信噪比低于-5dB时，|δ|越大性能有较大的差异性，所以-5dB是该算法的门限。所以，在一定信噪比下，本算法性能在噪声干扰下敏感度低。

3.2 与经典算法的估计性能比较

首先，将Triple_IN算法跟经典Quinn、Rife算法在SNR{-8dB，5dB}条件下与ACRB进行估计性能比较。从图3与图4的仿真结果，可以发现在0≤|δ|≤0.25时，Rife算法性能差距大，而Triple_IN算法在此时却可以逼近ACRB，但在0.25≤|δ|≤0.5时逐渐偏离理论曲线；Quinn正好与Triple_IN算法相反，在偏离量化频点时精度越高。同时，相对经典算法可以看出本算法在信噪比变化下的曲线相对平稳，而其他经典算法曲线抖动变化大即相对可靠性较低。

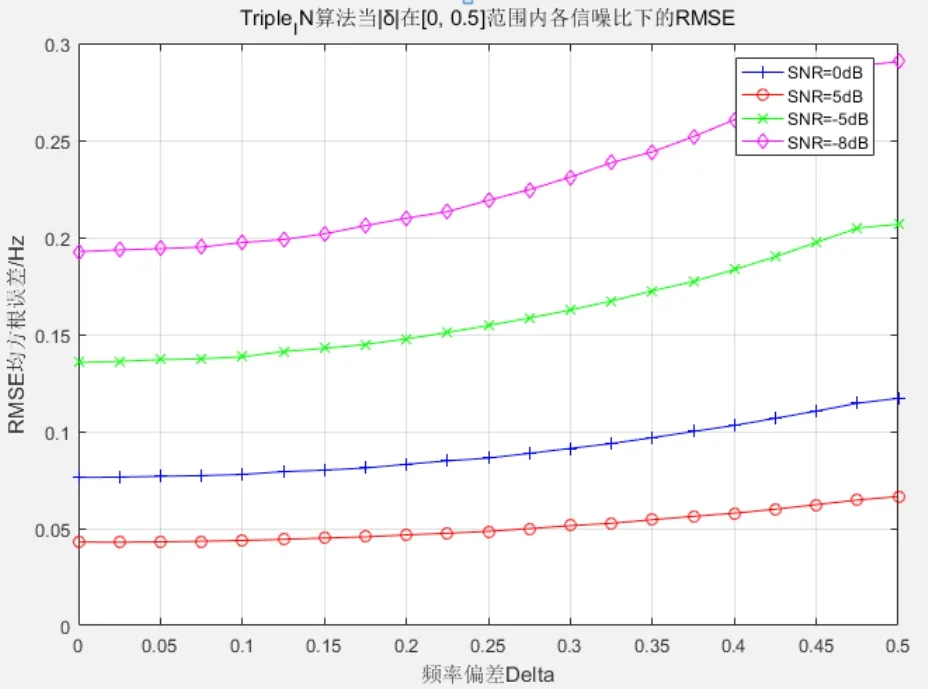
图1 Triple_IN算法|δ|在[0, 0.5]内各信噪比下的RMSE

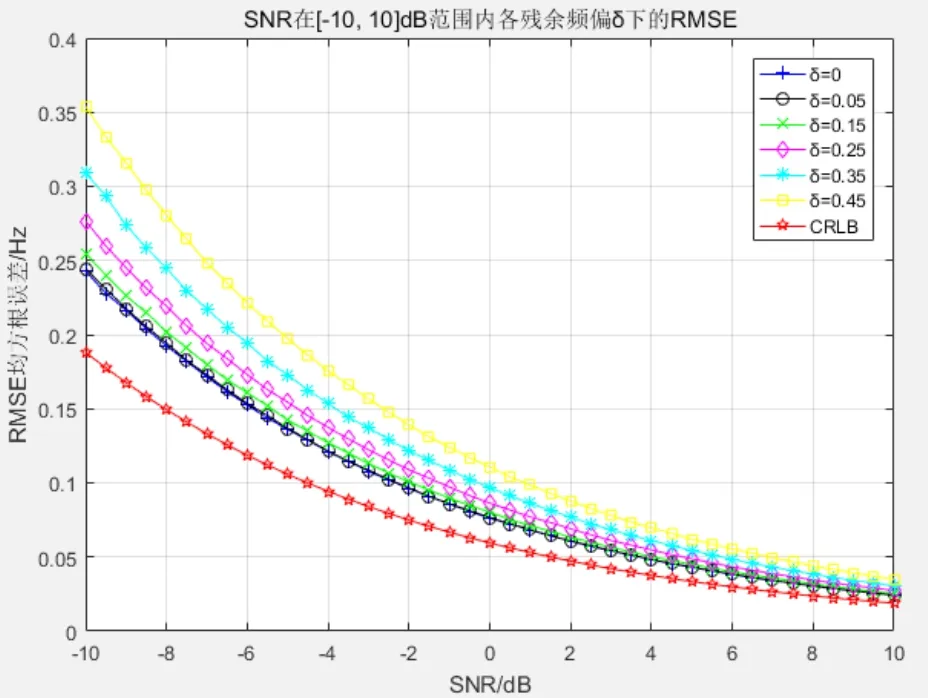
图2 SNR在一定范围内各残余频偏δ下的RMSE

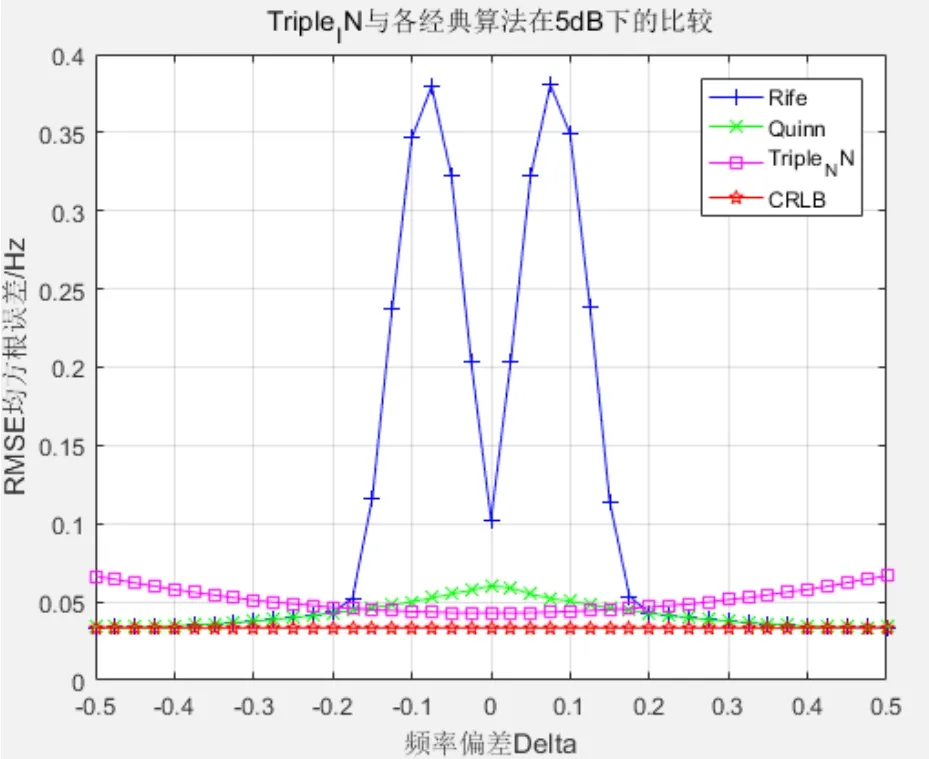
图3 Triple_IN与各经典算法在5dB下的RMSE比较

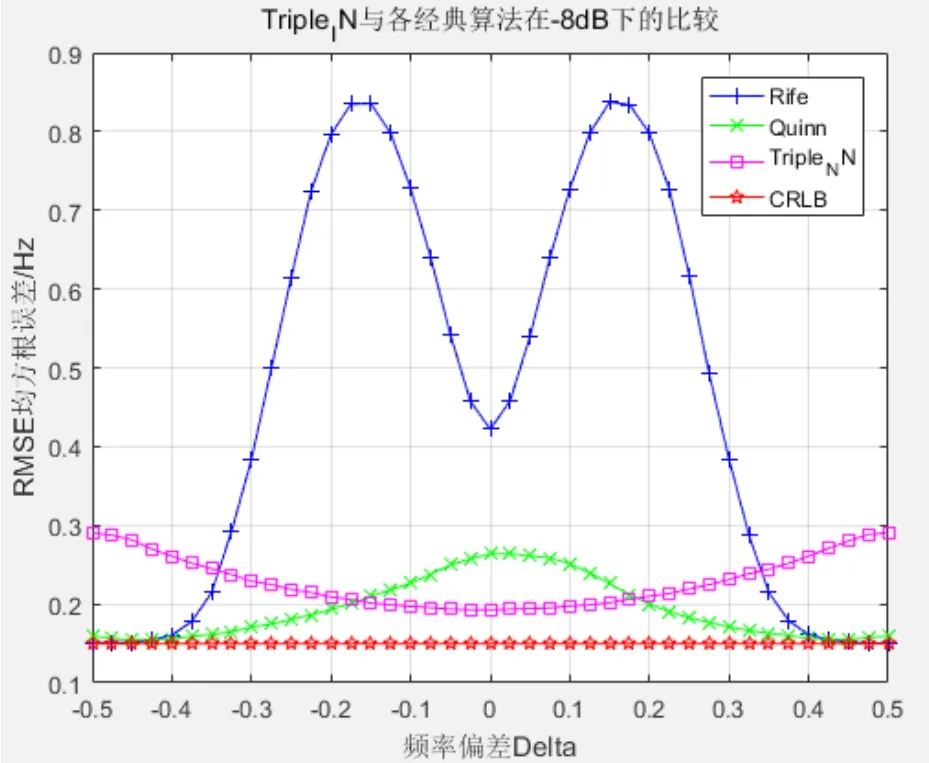
图4 Triple_IN与各经典算法在-8dB下的RMSE比较

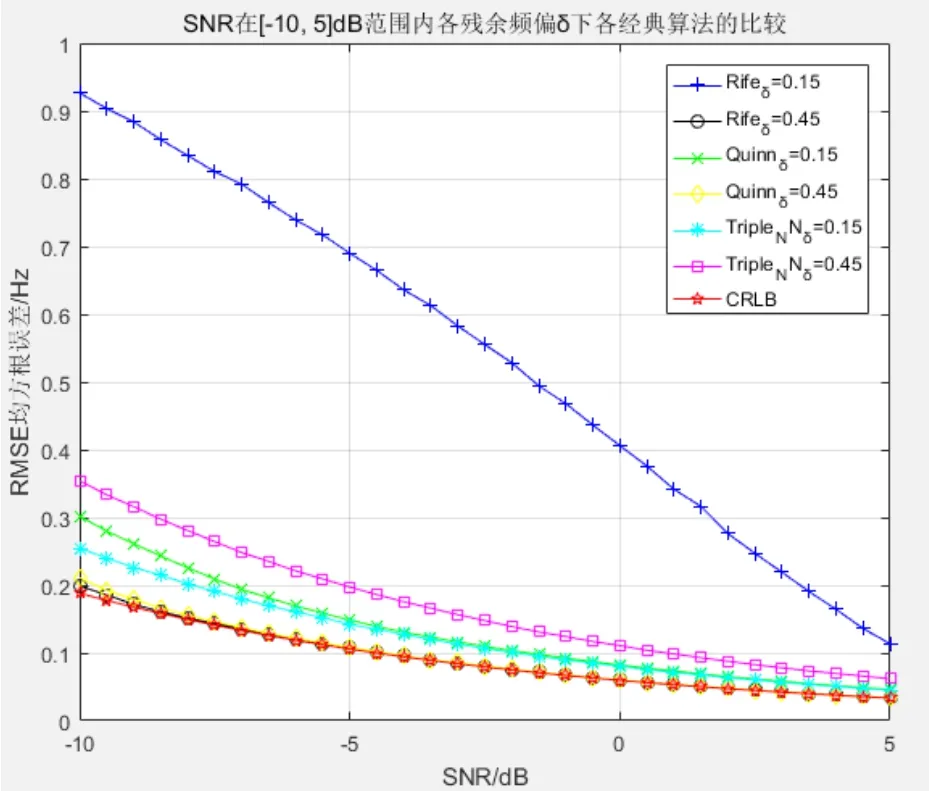
图5 SNR在[-10, 5]dB范围内残余频偏δ下各经典算法的比较

在|δ|=0.15和0.45的条件下进一步比较三者性能，仿真如图5所示。发现Rife算法对噪声最为敏感，Quinn算法接近量化频点时在噪声影响下曲线有明显变化，两者的性能在信噪比门限下都不如Triple_IN算法可靠性高。

4 计算量比较

如表1所示，Rife算法运算量小，但是算法本身的缺陷也较为明显。相比于Quinn算法，本算法少1次复数乘法运算，计算量小很多。虽然Quinn精度上略高于该算法，但在低信噪比的性能的稳定性和0≤|δ|≤0.25的估计准确性Triple_IN算法具有更高的表现。

5 结束语

本文通过研究经典频率估计插值算法的性能，提出了一种稳定度和精度较高、计算量较小的Triple_IN算法。频率的估计精度与信噪比及待观测时长有关，通过仿真结果分析，该算法在同等的低信噪比条件下，估计精度要远高于Rife算法，略低于Quinn算法。从估值效果即稳定性上该算法具有显著优势，其估值曲线不随|δ|和SNR值的变化而明显变化。运算量较Quinn算法节约一个复数乘法器，在FPGA工程实现过程中降低了复杂度，提高了计算精度。本算法已成功应用于实际研发项目且收效良好，故具备一定的推广应用价值。

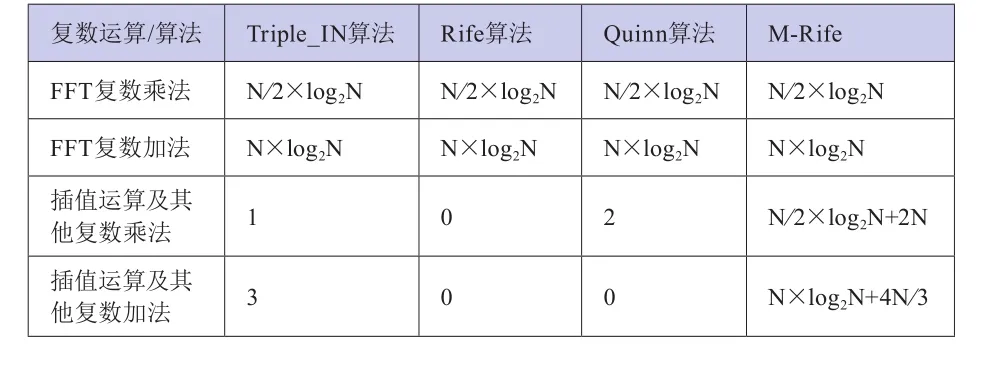
表1 各经典算法计算量大小的比较

[1] 谭晓衡，张毛．一种高精度的改进FFT频偏估计算法[J]．重庆理工大学学报（自然科学版），2010.7, 24(7): 72-75

[2] Rife D C and Boorstyn R R, Single tone parameter estimation from discrete-time obser-vations[J], IEEE Trans. Inf. Theory, 1974, 20(5): 591–598.

[3] Rife D C and Boorstyn R R, Multiple tone parameter estimation from discrete-time obser-vations[J], Bell Syst Tech J, 1976, 55(9): 1389–1410.

[4] Rife D C and Vincent G A. Use of the Discrete Fourier Transform in the measurement of Frequencies and Levels of tones[J]. Bell Syst Tech, 1978, 52(2):1285-1290.

[5] Quinn B G. Estimation of frequency, amplitude and phase from the DFT of a time series [J]. IEEE Trans. on SP. 1997, 45(3): 814-817.

[6] Quinn B G. Estimating frequency by interpolation using Fourier coefficients [J]. IEEE Trans-SP, 1994, 42(5): 1264-1268.

[7] 王旭东，刘渝，邓振淼．基于修正Rife算法的正弦波频率估计及FPGA实现[J]．系统工程与电子技术，2008. 30(4): 621-624

[8] 邓振淼，刘渝，王志忠．正弦波频率估计的修正Rife算法[J] ．数据采集与处理，2006, 21(4): 473–447

Ixia斩获Cloud China 2017云帆奖 “云计算优秀解决方案”

2016年5月12日，行业知名的网络测试、可视性和安全解决方案提供商Ixia宣布，在工业和信息化部主办的第五届中国国际云计算技术和应用展览会暨论坛（Cloud China 2017）中，凭借其业界领先的创新性产品 CloudLens™平台获得专家评审团与大众认可，斩获云帆奖年度“云计算优秀解决方案”。

云帆奖创立于2015年，由工业和信息化部国际经济技术合作中心设立，过去两年中，该奖项致力于表彰和推动中国云计算产业的创新发展与进步，为普及云计算建设应用起到了积极的引领作用。

当前，云计算技术发展迅猛，各企业对云计算的应用需求也与日俱增。 虽然云部署有诸多好处，但是访问和监测虚拟流量却充满挑战。 若无法对虚拟流量进行精细操作，将导致网络中出现盲点，影响应用性能或安全性。

Ixia 提供的可跨越所有云环境（公共云、私有云和混合云）的CloudLens™ 平台，通过采用情景感知和威胁情报结合的安全架构，以扩展虚拟探针和数据过滤来满足云客户期望的弹性需求，为用户带来前所未有的可视性。

Ixia中国区总经理张炜表示：“我们十分荣幸此次能够在Cloud China 2017云帆奖的评选中赢得年度‘云计算优秀解决方案’奖项， 这无疑是Ixia在中国市场展现技术实力的又一力证！”

An Faster and High Accurate Frequency Offset Estimator Based on FFT

Cai Qing, Chen Haiteng, Xu Yong
（Nanjing Panda Handa Technology Co., LTD., Nanjing, 210014）

A low rate of signal in the satellite communication system and a low signal to noise ratio (SNR) at the receiving side results in a normalized large frequency offset. To solve this problem, this paper proposed a interpolation algorithm of the Triple spectral lines based on Faster Fourier Transform by comparing the computational complexity.

Faster Fourier Transform; Frequency Estimation; Quinn Algorithm; Rife Algorithm; Cramer-Rao Lower Bound

10.3969/J.ISSN.1672-7274.2017.05.004

TN92

A文章编码：1672-7274（2017）05-0011-04

蔡 青，硕士，南京熊猫汉达科技有限公司高级工程师。

陈海腾，硕士，南京熊猫汉达科技有限公司工程师。

徐 勇，硕士，南京熊猫汉达科技有限公司工程师。