基于IDE-OSVR-ABAQUS的岩土力学参数反演方法

卢远富，包腾飞，李涧鸣，王 甜

(河海大学 a.水利水电学院; b.水资源高效利用与工程安全国家工程研究中心;c.水文水资源与水利工程科学国家重点实验室，南京 210098)

基于IDE-OSVR-ABAQUS的岩土力学参数反演方法

卢远富a,b,c，包腾飞a,b,c，李涧鸣a,b,c，王 甜a,b,c

(河海大学 a.水利水电学院; b.水资源高效利用与工程安全国家工程研究中心;c.水文水资源与水利工程科学国家重点实验室，南京 210098)

提出引入自适应因子的改进型差分进化算法(IDE)，并应用于优化在线支持回归机(OSVR)的核参数和惩罚参数，建立岩土体位移和岩土力学参数之间复杂非线性关系的动态最优IDE-OSVR模型，输入岩土体位移值直接输出岩土力学参数实现参数反演。通过均匀设计方法与ABAQUS正计算构建初始训练集，然后逐次反演并进行验算误差，将误差未达到预定阈值前的验算样本增添至训练集，使得IDE-OSVR模型不断在线学习，提高参数反演精度。将IDE-OSVR-ABAQUS反演方法应用于工程算例，并同几种典型方法对比。结果表明：该方法的岩土力学参数反演速度很快，反演精度很高，是一种合理的岩土力学参数反演方法。

改进型差分进化算法；在线支持回归机；ABAQUS ；参数反演；岩土体位移

1 研究背景

在实际岩土工程的数值模拟分析过程中，岩土力学参数值往往是影响岩土工程模拟分析结果的准确性、客观性以及实用性的重要因素。由于目前通过试验法获取岩土力学参数值存在周期较长、成本较高以及往往会与实际参数偏差较大的缺点，因此通过参数反演获取岩土力学参数一直都是岩土工程中的研究热点。

目前岩土参数反演主要分为直接参数反演和智能优化反演2种方法。直接参数反演一般首先构建正分析的计算解与实测值的误差目标函数，然后利用寻优算法与有限元等数值方法结合进行反演计算。由于单纯形法、复合形法和模式搜索法等为代表的传统直接优化反演方法存在易陷入局部最优和收敛性很差的缺点[1]，遗传算法[2](GA)、粒子群算法[3](PSO)及量子遗传算法[4](QGA)等全局寻优能力和收敛性很强的群智能算法被直接引入优化反演中，但仍然存在不同程度的依赖于反演初值的合理选取，且对于多参数反演有限元等正分析的调用次数大大增加甚至多达成百上千次,这很大程度上降低了反演的速度与实用性。近年来，岩土智能优化反演方法发展迅速，冯夏庭等[5]成功应用进化神经网络并结合遗传算法反演巷道力学参数；文辉辉等[6]利用BP神经网络反演藏珠洞隧道围岩力学参数并进而对隧洞作出实际稳定性评价和变形预测，但BP神经网络反演方法仍然存在着网络结构较难确定和处理小样本问题时易出现过拟合和不收敛的缺点。为此，不少学者在处理小样本问题时，性能良好的支持向量机(SVM)应用于岩土力学参数中，如赵洪波等[7]利用SVM正分析并结合PSO寻优对某地下隧洞的地应力进行反演并取得较好效果；杨云浩等[8]利用SVR正分析结合粒子群差分杂交算法(BBDE)应用于糯扎渡调压室的岩层弹塑性参数反演；漆祖芳等[9]利用SVR和粒子迁徙和变异的粒子群优化(MVPSO)算法成功反演某边坡岩体参数。以上的SVR反演方法均是基于特定训练集建立的岩土参数与岩土体位移非线性关系的静态最优SVR模型，该静态最优SVR模型的准确性对反演误差起着决定性的作用，但如何确定合理数量的训练样本目前仍无统一的方法和经验。此外SVR模型中核参数和惩罚参数对其预测精度和泛化能力有重要影响，但目前尚无统一的最优的优选方法。

本文首先提出引入自适应因子对基本差分进化算法(DE)进行改进，以进一步增强其全局寻优能力和收敛性并更好地避免早熟。最后将改进型差分进化算法(IDE)应用于优选对在线支持向量机(OSVR)有重要影响的核参数和惩罚参数。首先通过均匀设计构造较少数量的初始训练集，然后建立岩土体位移与岩土力学参数之间的复杂非线性关系动态IDE-OSVR模型，最后通过逐次反演和自动化验算误差产生“高质量”的新样本增添至训练集使得IDE-OSVR模型能够动态在线学习，更好地建立岩土体位移与岩土力学参数的精确非线性关系，以进一步提高反演的精度。通过将IDE-OSVR和ABAQUS有限元计算结合编写IDE-OSVR-ABAQUS反演程序并应用于算例中表明：IDE-OSVR-ABAQUS方法的反演效率很高，是一种合理的岩土力学参数反演方法。

2 改进的差分进化算法(IDE)

2.1 基本差分进化算法

基本差分进化算法(DE)于1995年由Storn等[10]提出，是一种全局寻优能力较强并且收敛速度较快的寻优算法，其基于实数编码的进化策略，因而操作简便，容易实现。 基本DE算法主要包括4个过程：①种群初始化;②变异操作;③交叉操作;④选择。DE算法的具体过程可以参考文献[11]。

对基本DE算法效果有重要影响的参数主要有：

(1) 种群总数N,N值要根据实际问题选定，一般取值范围为[20,50]，N值越大，种群多样性越强，搜寻到最优解的概率越大，但计算时间也随之越长。

(2) 变异因子F，F值主要对变异操作中产生新的个体有重要影响，取值区间为(0,2)。

(3) 交叉因子CR，CR值主要对交叉操作产生重要影响，取值区间为(0,1)。

2.2 改进的差分进化算法

由于变异因子F和交叉因子CR对DE算法的全局寻优能力和收敛性影响很大，为了更好地平衡DE算法全局寻优能力和收敛速度并避免早熟，本文设计一种自适应因子λ对基本DE算法中的变异因子F和交叉因子CR值的设置进行了改进，改进公式为：

(1)

(2)

(3)

式中：G为最大进化代数；g为当前进化代数。根据经验公式[12]，Fmax取0.9，Fmin取0.2。由此可得式(2)中变异因子F的变化范围为[0.2,0.9]。在种群进化前期F的值较大，这样可以增加种群的多样性使得IDE更容易找到全局最优点，在种群进化中后期，由于变异因子F的变小使得中后期的收敛速度得以加快，总体上使得良好的全局搜索能力在进化前期得以保持，而后期保持较好的收敛性。式(3)中CR为交叉因子，同理根据经验公式，CRmax取0.5，CRmin取0.1，由此可得式(3)中交叉因子CR的变化范围为[0.1,0.5]。种群进化前期时CR的值较大，使得在保证种群多样性的同时收敛性得到适当增强，种群进化中后期CR的值较小，可以避免早熟现象并与变异因子一起平衡算法性能。

3 在线支持回归机(OSVR)建模方法

支持回归机(SVR)是基于引入不敏感函数的支持向量机(SVM)中转化而来[13]，因此SVR继承了SVM在训练小样本集时具有很好的稳定性和泛化能力以及对维数不敏感的优点。OSVR与SVR的区别是OSVR对于样本训练学习不是一次性离线完成的，而是通过样本数据的逐一加入反复优化[14]，由此实现了动态学习。由于OSVR的训练样本集不断变化，因此选用训练速度很快的序列最小最优化算法[15-16](Sequential Minimal Optimization ,SMO)作为其训练算法。OSVR建模过程中惩罚参数和核函数的选取对OSVR的训练学习的稳定性以及推广能力有重要影响，本文中的OSVR建模的核函数选用性能良好且核函数参数很少的RBF径向基函数，即

(4)

则影响本文的OSVR的精度的主要参数为惩罚参数C和核参数σ。由于式(4)中核参数σ敏感性很高，利用式(5)进行变换。

(5)

利用改进的差分进化算法(IDE)对C和h进行寻优计算。适应度函数为C和h利用交叉验证(CV)条件下的均方差(MSE)，损失函数选用ε线性不敏感损失函数。

IDE-OSVR建模应用在岩土参数反演中，主要能产生并逐一添加新的训练样本，通过动态学习建立岩土体位移与岩土力学参数复杂非线性关系的最优IDE-OSVR模型，以此提高反演计算的精度。利用IDE-OSVR建模进行参数反演的主要步骤如下：

(1) 根据初始样本集进行预处理，并通过对训练样本集的学习训练建立IDE-OSVR模型。

(2) 输入实测点位移值至步骤(1)中的OSVR模型中得出待反演参数值。

(3) 对步骤(2)中的反演参数进行正计算，得出测点计算值并与实测值比较，计算误差，若误差大于预定阈值，则进入步骤(4)，若误差小于或等于预定阈值，则转向步骤(6)。

(4) 将步骤(3)中的验算的反演参数及其对应点的位移值作为一个新的样本点增添至训练样本集，并检查训练集样本数目是否大于预定最大值，若否则转至步骤(2)，若是则转向步骤(5)。

(5) 反演终止，并重新调整相关模型参数，并再次运行反演程序。

(6) 反演完成，输出待反演的参数组合。

图1 IDE-OSVR-ABAQUS参数反演流程Fig.1 Flowchart of parameter inversion based on improved differential evolutionalgorithm, online support vector regression and ABAQUS

4 IDE-OSVR-ABAQUS反演方法

在前述章节的基础上，利用IDE-OSVR方法进行参数反演的过程中，初始训练样本集构建和误差验算中均需要反复调用ABAQUS求解器进行有限元计算。IDE-OSVR-ABAQUS反演方法的流程见图1，本文利用MATLAB语言编程反演程序，故该方法实施中还涉及以下几个问题。

4.1MATLAB语言与ABAQUS的接口问题

接口问题即利用MATLAB反演主程序中调用ABAQUS求解器进行计算，该问题可以通过MATLAB语言的system命令具有同步调用的机制优势解决。

4.2 待反演的参数自动化修改以及有限元结果文件读取

根据逐次的参数反演值，利用MATLAB中的strrep命令修改命令流(inp)文件中的待反演参数值并提交ABAQUS正分析计算。利用MATLAB的fopen打开DAT结果文件，提取测点的位移计算值，并通过误差函数计算误差值。

4.3 利用IDE进行OSVR建模进行参数优选

利用IDE对OSVR的惩罚参数C和核函数参数h进行优选。进行优选步骤：①根据C和h的取值范围对种群初始化;②采用自适应变异因子F对种群进行变异操作产生新个体，之后利用自适应的交叉因子CR进行交叉操作；③采用IDE-OSVR拟合数据与训练集样本数据的均方差(MSE)作为适应度值函数，计算新个体的适应度值;④选择操作并判断是否满足终止条件并选择最优个体，即适应度函数值最小时对应的C和h的值；⑤输出训练集一定时的最优参数C和h的值，此时对应建立的IDE-OSVR模型即为反映岩土体位移与反演参数非线性关系的最优模型。

4.4 验算误差的函数设定及OSVR训练样本集的更新

由于IDE-OSVR-ABAQUS反演方法会逐一增加训练样本来实现在线学习，逐渐增添新样本的流程为：将之前反演参数代入ABAQUS命令流文件正算位移，并将正算位移与实测位移对比检验误差是否超过预定阈值，若误差超过预定阈值，则将此反演参数及其位移作为新样本增添至训练集。若误差不超过预定阈值，则此时参数组合值可作为真实的岩土力学参数值，也即视为满足工程控制精度且可用的参数值。若在线添加的新样本数目达到预设最大值Kmax，则通过调整初始反演参数组合或者增大在线添加样本数目再次进行反演。本文误差函数采用最大相对误差[17]来表征误差大小,即

(6)

5 工程算例

通过比利时BoomClay泥岩隧洞[18]开挖工程进行岩土力学参数反演来验证本文方法的合理性与有效性以及编写的MATLAB反演主程序的正确性。该隧洞截面为直径4.84m的圆形，其埋深为223m，初始地应力和孔隙水压力均为2.25MPa。本算例采用摩尔-库伦模型计算，并通过初始地应力平衡和生死单元来模拟该隧洞开挖。该工程的基本力学参数见表1，由对称性，仅取一半进行简化建模，其有限元计算模型如图2，对该模型进行弹塑性流固耦合分析，有限元网格类型设CPE4RP单元，共1 832个，节点1 906个，此外选取如下图3测点位置对应的有限元网格模型的9个节点作为变形观测点(图2(b)中9个测点号为图2(a)中有限元计算模型的节点编号)。

表1 基本力学参数

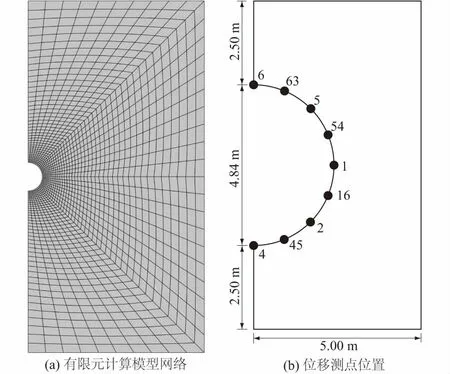
图2 有限元计算模型网络及位移测点位置Fig.2 Model for finite element calculation anddistribution of displacement measurement points

本算例反演3个力学参数：弹性模量，内摩擦角，黏聚力。首先将本算例中软岩弹性模量取800 MPa，内摩擦角18°，黏聚力取1.5 MPa进行计算，并取图2(b)中9个测点有限元计算位移值(如表2)作为反演所需的实测位移值，为模拟真实测值的情况，考虑到实际测量误差因素，一般选用测点测值较大的参数值(本文选位移值≥1 cm的值)进行参数反演。通过IDE-OSVR-ABAQUS反演程序得到的3个待反演参数，再将反演所得的参数代入ABAQUS正分析计算得到的相应测点位移值并同真实测点位移值对比分析，得出最终的反演参数值。

表2 各测点实测位移值

首先利用均匀设计表[19]设计30个反演参数组合，由于反演参数个数为3，根据均匀使用表的用法，选取第1列和第9列以及第10列并结合待反演参数的反演区间(见表3)构建初始反演参数组合(见表4)，并根据ABAQUS正分析计算这30个参数组合对应的位移值。

表3 待反演参数区间

由于3个待反演参数之间的数量级差距很大，为消除数量级以及量纲引起的信息变异，同时提高训练学习反演的速度，拟对表4进行数据预处理，本算例中将表4中每列数据以及经过ABAQUS计算之后相应测点的位移值进行归一化至区间[0.1,0.9]，即

(7)

考虑到不同测点位移值存表示位移方向正负之分，故式(7)中规定Xmax和Xmin分别对应为表4中30个待反演参数组合中位移值的绝对值最大值与最小值(由于每一个测点的X向和Y向变形趋势一致，故不会存在正负号混乱问题)。

利用IDE对OSVR参数进行优选以建立算例中测点位移值与反演参数的复杂非线性关系的最佳IDE-OSVR模型，由于考虑到OSVR的C和h两个参数寻优范围较大，本文对IDE种群总数设为40，最大进化代数设为100。利用根据IDE-OSVR-ABAQUS原理编写的MATLAB反演程序进行反演，得出结果见表5，经过ABAQUS验算反演结果的对应的测点位移计算值与实测位移值已经非常接近，其与测点实测位移值的最大相对误差在1%以内，可以认为反演出的岩土参数值为工程中可以应用的真实值。图3、图4分别为给定参数条件下与反演结果参数条件下的水平位移场与竖直位移场的等值线图，通过水平位移场与竖直位移场2组等值线图的对比可见反演结果与真实值很接近，另外通过与预先设置的真实值对比(表5)，也进一步说明以上计算的正确性。

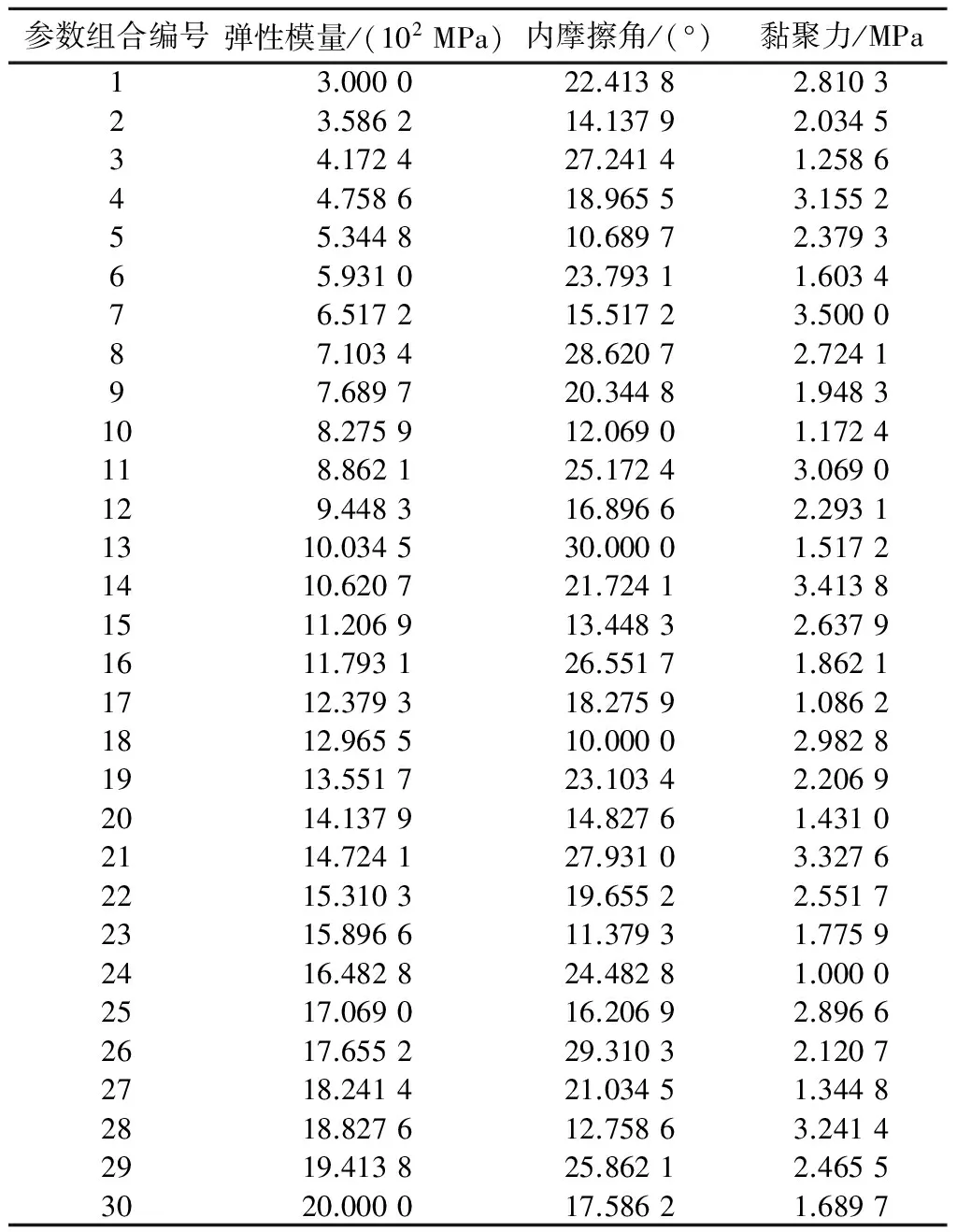
表4 反演参数均匀设计组合

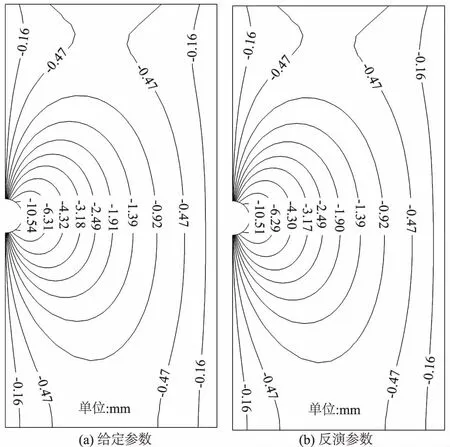
图3 给定参数和反演参数条件下水平位移场Ux Fig.3 Horizontal displacement field under the condition ofgiven parameters and inversion parameters

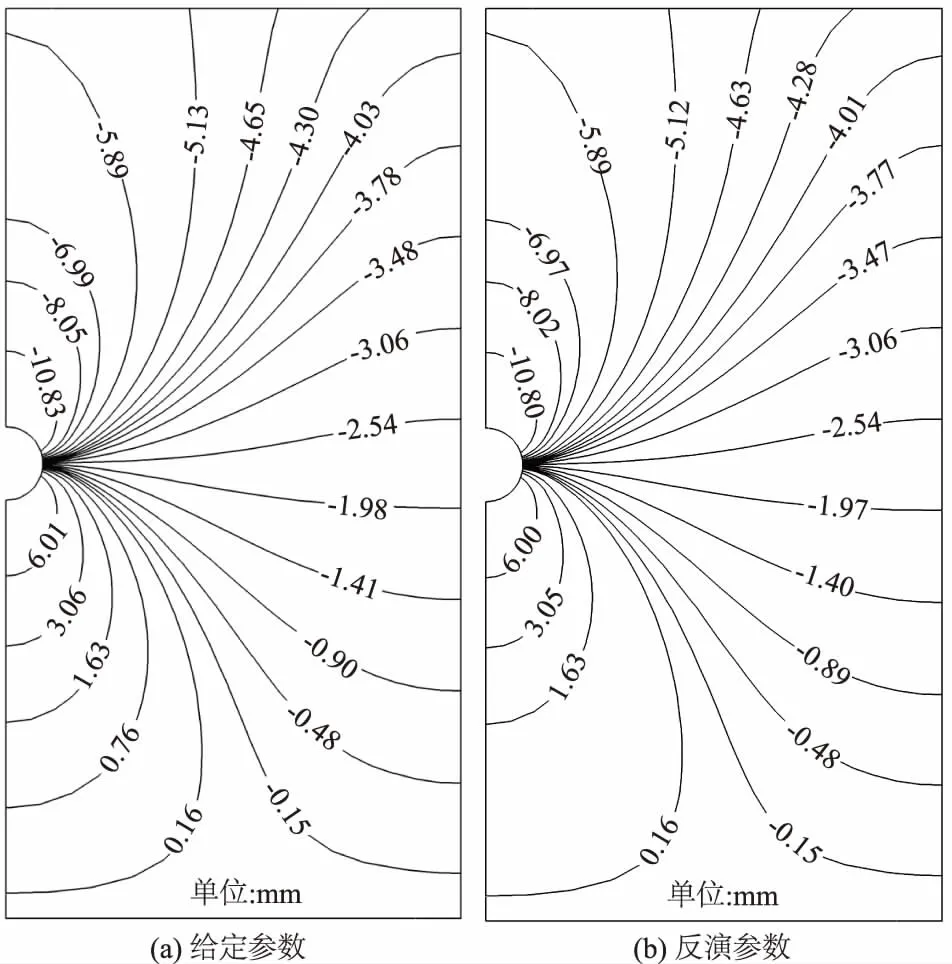
图4 给定参数和反演参数条件下竖直位移场Uy Fig.4 Vertical displacement fields under the condition ofgiven parameters and inversion parameters

将本文方法与遗传算法(GA)直接优化反演法[2]， BP神经网络反演法以及标准的SVR方法以及DE-OSVR方法的结果进行对比分析， 其结果对比表见表6。 通过将本文方法与GA直接优化反演法对比可以发现两者的反演参数精度比较相近， 但本文所用IDE-OSVR建模的方法调用ABAQUS求解器仅33次， 仅为GA直接优化反演方法调用求解器次数的56.8%， 节省了大量计算时间， 反演效率得以提高； 为更好进行对比分析， 本文中BP神经网络的训练样本也设置为SVR训练的30个初始样本集， 通过训练可以发现本文中的BP神经网络训练很难收敛且结果波动很大， 这与训练样本过少有很大关系，表6中显示结果为多次训练中最好结果。

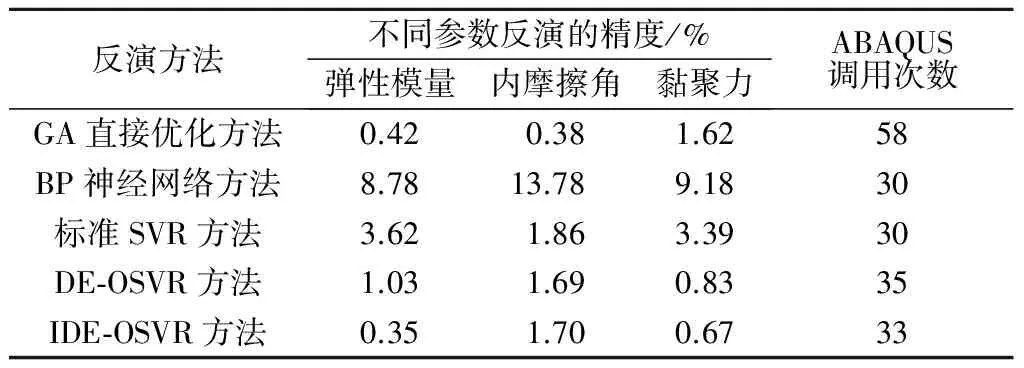
表6 典型参数反演方法结果对比

从BP神经网络与标准的SVR方法的反演结果对比可以看出，在ABAQUS进行正分析计算被调用次数(均为30)相同的情况下，标准SVR方法反演参数的相对误差均大大低于BP神经网络进行参数反演的相对误差，这表明标准SVR对于小样本有较好的学习和推广能力，将IDE-OSVR方法反演结果同标准SVR结果相比可以看出，在增加很少数量的学习样本集之后，反演的各参数精度均得到很大改善。通过分析可以发现这是由于通过30组的初步训练，虽然初始反演的参数值经过验算误差大于预定的阈值，但是反演参数值同真实值已经比较接近，可以将此类新样本称之为“高质量”的学习样本，通过“高质量”样本的逐渐添加，使得岩土体位移与反演参数之间复杂的非线性关系的动态最优IDE-OSVR模型精度更高，使得参数反演的精度也有所提高。将DE-OSVR方法与IDE-OSVR方法的结果进行对比可以看出，IDE-OSVR反演误差较DE-OSVR有一定的减小，且IDE-OSVR调用ABAQUS有限元计算的次数较DE-OSVR的次数少，由此表示改进之后的差异进化算法(IDE)对在线支持回归机(OSVR)的全局寻优能力有一定的增强，使得IDE-OSVR模型更好地反映了算例中测点位移与岩土体力学参数的复杂非线性关系，使得需要新增的“高质量”新样本的数目减少，反演计算效率和速度得以提高，这也进一步反映了本文改进差分进化算法优化OSVR模型参数的有效性。

6 结 论

(1) 引入自适应因子的改进型差分进化算法(IDE)的寻优能力较引入前进一步增强，且有良好的收敛性并更好地避免早熟现象，是一种可以适用于在线支持回归机(OSVR)参数寻优且性能良好的优化方法。

(2) 通过逐次反演产生的新的“高质量”样本来动态更新训练集，改进型差分算法的在线支持回归机(IDE-OSVR)能够充分利用通过动态更新的训练集的信息进行在线学习，更好地动态反映岩土体位移与反演参数之间的复杂非线性关系，进而实现快速动态反演且反演精度很高。

(3) 将IDE-OSVR-ABAQUS反演方法同标准的SVR反演方法相比，在增加较少数量的新样本的情况下，能进一步地提高参数反演的精度；其同BP神经网络反演方法相比对于小样本、过拟合以及收敛性等问题的解决具有很大优势；其同GA直接优化反演相比参数反演速度大大提高，且反演精度亦有一定的提高，因此IDE-OSVR-ABAQUS反演方法有较好的工程应用价值，且本方法也可以考虑进一步研究改进以推广到除岩土力学参数之外的混凝土弹性模量反演，渗流反演等其他反分析领域。

[1] 李 枫. 岩体力学参数的非线性随机反演优化方法的研究[J].长江科学院院报，2006，23(3)：51-54.

[2] 贾善坡. 基于遗传算法的岩土力学参数反演及其在ABAQUS中的实现[J].水文地质工程地质，2012，39(1)：31-35.

[3] 韩 峰，徐 磊，张太俊. 坝基岩体力学参数的PSO-ABAQUS 联合反演[J].河海大学学报，2013，41(4)：321-325.

[4] 曹明杰，曹 鑫，徐政治. 量子遗传算法在混凝土重力坝综合弹性模量反演中的应用[J].长江科学院院报，2016，33(4)：111-114.

[5] 冯夏庭，张治强，杨成祥，等. 位移反分析的进化神经网络方法研究[J].岩石力学与工程学报，1999，18(5)：497-502.

[6] 文辉辉，尹健民，秦志光，等. BP神经网络在隧道围岩力学参数反演中的应用[J].长江科学院院报，2013，30(2)：47-51，56.

[7] 赵洪波. 基于微粒群优化的智能位移反分析研究用[J].岩土工程学报，2006，28(11)：2035-2308.

[8] 杨云浩，徐卫亚，聂卫平. 基于ε-SVR与PSO-DE的岩层弹塑性参数反演及应用[J].中国矿业大学学报，2009，40(1)：95-102.

[9] 漆祖芳，姜清辉，周创兵，等. 基于ε-SVR和MVPSO算法的边坡位移反分析方法及其应用[J].岩石力学与工程学报，2013，32(6)：1185-1196.

[10]STORN R, PRICE K. Differential Evolution-A Simple and Efficient Heuristic for Global Optimization over Continuous Spaces[J]. Journal of Global Optimization, 1997, 11(4):341-359.

[11]刘 琛，林 盈，胡晓敏.差分演化算法各种更新策略的对比分析[J].计算机科学与探索，2013，7(11):983-993.

[12]许小健，黄小平，钱德玲.自适应加速差分进化算法[J].复杂系统与复杂性科学，2008，5(1):87-92.

[13]卢远富，包腾飞，李涧鸣，等. 基于改进型混合蛙跳算法的支持回归机大坝变形预测模型[J].三峡大学学报(自然科学版)，2015，37(5):14-18.

[14]王定成，姜 斌.支持向量机控制与在线学习方法研究进展[J].系统仿真学报，2007，19(6):1177-1512.

[15]王定成.支持向量机建模预测与控制[M].北京：气象出版社，2009.

[16]PLATT J. Using Analytic QP and Sparseness to Speed Training of Support Vector Machines[C]∥Neural Information Processing Systems Foundation. Proceedings of Advances in Neural Information Processing Systems. November 29-December 4,1999:557-563.

[17]向 文，张强勇，张建国.坝区岩体蠕变参数解析——智能反演方法及其工程应用 [J].岩土力学，2015，36(5):1505-1512.

[18]贾善坡. Boom Clay泥岩渗流应力损伤耦合流变模型、参数反演与工程应用[D].武汉：中国科学院武汉岩土力学研究所，2009.

[19]方开泰.均匀设计与均匀设计表[M].北京：科学出版社，1994.

(编辑：赵卫兵)

Inversion of Geotechnical Mechanical Parameters Based onImproved Differential Evolution Algorithm, Online Support Vector Regression and ABAQUS

LU Yuan-fu1,2,3, BAO Teng-fei1,2,3, LI Jian-ming1,2,3, WANG Tian1,2,3

(1.College of Water Conservancy and Hydropower, Hohai University, Nanjing 210098, China; 2.National Engineering Research Center of Water Resources Efficient Utilization and Engineering Safety, Hohai University, Nanjing 210098, China; 3.State Key Laboratory of Hydrology-Water Resources and Hydraulic Engineering, Hohai University, Nanjing 210098, China)

An improved differential evolution algorithm (IDE) is proposed by introducing adaptive factor and is applied to optimizing the kernel parameter and penalty parameter of online support vector regression (OSVR). A dynamic optimal IDE-OSVR model which reflects the complex nonlinear relationship between rock and soil mass displacements and geotechnical parameters is established. The inversion of parameters can be accomplished by inputting the soil mass displacements in the IDE-OSVR model. The initial training set is designed with uniform design method and ABAQUS calculation, then the errors of successive inversed parameters are checked, and the checked sample will be added to training set if the error is greater than the predetermined threshold. Through the continuous online learning process, the precision of parameters inversion by IDE-OSVR model can be enhanced. The inversion method based on IDE-OSVR-ABAQUS is applied to an engineering example and the result is compared with those of typical methods. The comparison result shows that the IDE-OSVR-ABAQUS inversion method is very fast with high accuracy, hence is a reasonable method for the inversion of geotechnical mechanics parameters.

IDE; OSVR; ABAQUS; parameters inversion;soil mass displacement

2016-03-21；

2016-04-21

卢远富(1991-)，男，湖北麻城人，硕士研究生，研究方向为水工建筑物安全监控，(电话)15295514300(电子信箱)yuanfulu@163.com。

包腾飞(1974-)，男，湖北黄冈人，教授，博士生导师，研究方向为水工建筑物安全监控、评估及反馈，(电话)025-83786706(电子信箱)baotf@hhu.edu.cn。

10.11988/ckyyb.20160259

2017,34(6):81-87

TU45

A

1001-5485(2017)06-0081-07