一阶逻辑推理系统中有关量词推理规则的研究

王文龙，张博锋(.喀什大学计算机科学与技术学院，中国 喀什 844000;.上海大学计算机工程与科学学院，中国 上海 0004)

一阶逻辑推理系统中有关量词推理规则的研究

王文龙1，张博锋2
(1.喀什大学计算机科学与技术学院，中国 喀什 844000;2.上海大学计算机工程与科学学院，中国 上海 200041)

通过对两种一阶逻辑自然推理系统中有关量词的推理规则及其成立条件的比较分析，给出形式简单、直观的有关量词的推理规则和合理、严谨的成立条件，从而保证在使用这些规则时，既保留了直观性，又消除了不严格性，并能准确把握成立条件.

一阶逻辑；全称量词；存在量词；推理规则；成立条件

文献[1～12]描述了一阶逻辑自然推理系统中有关量词的推理规则，即全称量词引入规则、全称量词消去规则、存在量词引入规则、存在量词消去规则，在自然推理系统中具有重要作用.但由于使用这些推理规则时必须要满足一定条件，而这些条件不容易准确把握.另一方面，关于量词的推理规则，不同的自然推理系统会有不同的表示形式，使用这些规则的要求也有所不同.基于以上两方面因素，在使用量词的推理规则时，极易产生问题.因此，本文对两种一阶逻辑自然推理系统中有关量词的推理规则及其成立条件进行比较分析，并根据分析，阐述在使用这些推理规则过程中应采取的表示形式及成立条件，从而保证在使用这些规则时，既保留规则的直观性，又消除规则的不严格性，并能准确把握成立条件.

1 全称量词消去规则分析

1.1 不同表示形式

(1)在文献[1]中的形式

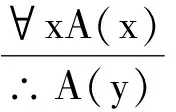
(1)

两式成立的条件是：

a.在第一式中，取代x的y应为任意的不在A(x)中约束出现的个体变项；

b.在第二式中，c为任意个体常项；

c.用y或c去取代A(x)中的自由出现的x时，一定要在x自由出现的一切地方进行取代.

(2)在文献[2]中的形式

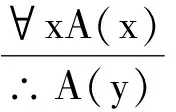
(2)

其中x,y是个体变项符号，c是个体常项符号，且在A中x不在∀y和∃y的辖域内自由出现.

1.2 实例比较与分析

式(1)与式(2)形式一致，但成立条件描述不同.

对式(1),令A(x)=∃yF(x,y)，F(x,y)表示x>y，则∀xA(x)=∀x∃yF(x,y).在个体域实数集中，解释为：对于任意的实数x都存在实数y，使得x>y，此命题为真.而由式(1)第一式有∀x∃yF(x,y)⟹∃yF(y,y)，可解释为：存在实数y使得y>y，此命题为假.由此在推理中出现了由真推理假的情况，推理错误.错误原因主要是使用式(1)时，用来替代x的y在A(x)=∃yF(x,y)中约束出现，因此为保证正确使用该推理规则，需满足条件(a)，即替代x的y应为任意的不在A(x)中约束出现的个体变项.从另一个角度看，错误的原因主要是在A(x)=∃yF(x,y)中，x在∃y的辖域中自由出现，即x在指导变元y的辖域内自由出现，因此为保证正确使用该推理规则，需满足在A中x不在∃y和∀y的辖域中自由出现的条件.

式(2)推理规则形式化描述为：∀xA(x)→A(y)为永真.证明如下：

∀xA(x)→A(y)⟺∀xA(x)→A(x)(代替规则)，此等值式成立要求A(y)中不含x的出现，即在A中x不在∀y和∃y的辖域中自由出现；而对于∀xA(x)→A(x)，若∀xA(x)为真，则A(x)必为真，∀xA(x)→A(x)为真；若∀xA(x)为假，则∀xA(x)→A(x)为真.因此∀xA(x)→A(x)⟹1即∀xA(x)→A(y)为永真，成立条件是在A中x不在∀y和∃y的辖域中自由出现.

不难发现，式(1)和式(2)形式相同，成立条件是同一问题的不同描述.式(1)的条件直观但更偏重于语义理解，式(2)的条件较严谨，是等值演算所要求的，与具体的解释无关.

2 全称量词引入规则分析

2.1 不同表示形式

(1)在文献[1]中的形式

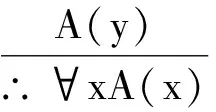
(3)

该式成立的条件是：

a.无论A(y)中自由出现的个体变项y取何值，A(y)应该均为真；

b.取代自由出现的y的x，也不能在A(y)中约束出现.

(2)在文献[2]中的形式

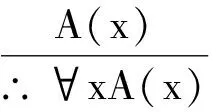
(4)

其中x是个体变项符号，且不在前提的任何公式中自由出现.

2.2 实例比较与分析

式(3)和式(4)形式略有不同，成立条件的描述也不同.

对式(3),令A(y)表示y是偶数，在个体域整数集中，解释为：整数y是偶数，此解释依据y的取值可为真亦可为假.而由式(3)有A(y)⟹∀xA(x)，∀xA(x)可解释为：所有整数都是偶数，此命题为假.由此在推理中出现了由真推理假的情况，推理错误.错误原因是使用式(2)时，对于y取不同的值，A(y)可真可假，因此为保证正确使用该推理规则，需满足条件(a)，即无论A(y)中自由出现的个体变项y取何值，A(y)应该均为真.

令A(y)=∃xF(x,y)，F(x,y)表示x>y，在个体域实数集中，A(y)解释为：对于实数y都存在实数x，使得x>y，此命题为真.而且对于任意的实数y，此命题均为真，满足条件(a).而由式(3)有，A(y)⟹∀xA(x),∀xA(x)=∀x∃xF(x,x)，可解释为：对于任意的实数x，存在实数x使得x>x，此命题为假.由此在推理中出现了由真推理假的情况，推理错误.原因主要是使用式(3)时，用来替代y的x在A(y)=∃xF(x,y)中约束出现，因此为保证正确使用该推理规则，需满足条件(b)，即取代自由出现的y的x，也不能在A(y)中约束出现.从另一个角度看，错误的原因是当y的值取x时，不能保证A(x)=∃xF(x,x)为真，因此，为保证正确使用该推理规则，需满足条件(a).

使用式(4)有如下推理证明：前提：P(x)→Q(x),P(x).结论：∀xQ(x).

证明：①P(x)→Q(x) ②P(x) ③Q(x) ④∀xQ(x)(式(4)).

给出此推理的一个解释，在个体域整数集中，P(x)表示x是偶数，Q(x)表示x被2整除.则P(x)→Q(x)为真，P(x)真值不确定，∀xQ(x)为假，因此此推理错误.原因是在③推理④的过程中，使用式(4)时，x在前提中自由出现.因此为保证正确使用该推理规则，需满足x不在前提的任何公式中自由出现的条件.

对比式(3)和式(4)，可对式(3)做如下演算：A(y)⟺A(x)(代替规则)，此等值式成立要求A(y)中不含x的出现，此时，式(3)可改为A(y)⟺A(x)⟹∀xA(x)，即为式(4)，两式在满足A(y)中不含x的出现的条件时是相同的.不难看出，式(4)使用时所需条件不完备，而且可以由式(3)推导出，因此，完全可以用式(3)替代式(4).

3 存在量词消去规则分析

3.1 不同表示形式

(1)在文献[1]中的形式

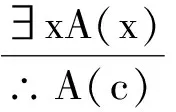
(5)

该式成立的条件是：

a.c是使A为真的特定的个体常项；

b.c不在A(x)中出现；

c.A(x)中除自由出现的x外，还有其他自由出现的个体变项，此规则不能使用.

(2)在文献[2]中的形式

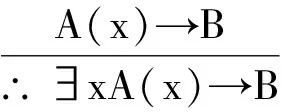
(6)

其中x是个体变项符号, 且不在前提的任何公式和B中自由出现.

3.2 实例比较与分析

式(5)和式(6)形式不同，成立条件的描述也不同.

令A(x)=F(x,5)，表示x>5，在个体域整数集中，∃xA(x)解释为：存在整数x>5，此命题为真.而由式(5)有∃xA(x)⟹A(c)，若替代x的c取大于5的整数，则A(c)=F(c,5)为真，推理正确；若替代x的c取小于5的整数，则A(c)=F(c,5)为假，由此在推理中出现了由真推理假的情况，推理错误，原因是替代x的c不能使A(c)=F(c,5)为真；若替代x的c取整数5，则A(c)=F(5,5)为假，由此在推理中出现了由真推理假的情况，推理错误，此时错误的原因是替代x的5在A(c)=F(c,5)已经出现.因此，为保证正确使用该推理规则，需满足条件(a)和(b)，即c是使A为真的特定的个体常项和c不在A(x)中出现.从另一角度看，两种错误的原因都是因为替代x的c不能保证A(c)=F(c,5)为真，因此，为保证正确使用该推理规则，需满足条件(a).

令A(x)=F(x,y)，F(x,y)表示x>y，在个体域实数集中，∃xA(x)=∃xF(x,y)解释为：存在实数x，使得x>y，此命题为真.而由式(5)有∃xA(x)⟹A(c)⟺F(c,y)，显而易见，F(c,y)为假，由此在推理中出现了由真推理假的情况，推理错误.原因是在A(x)=F(x,y)中，除了自由出现的x外还有自由出现的y，因此，为保证正确使用该推理规则，需满足条件(c)，即A(x)中除自由出现的x外，还有其他自由出现的个体变项，不能使用此规则.从另一角度看，错误的原因是因为替代x的c不能保证A(c)=F(c,y)为真，因此，为保证正确使用该推理规则，需满足条件(a).

对式(6)结论进行等值演算，∃xA(x)→B⟺∀x(A(x)→B)(量词辖域收缩与扩张等值式)，此式成立要求B中不含x的出现，则式(6)变为

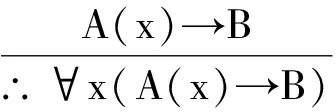
不难发现此式可由式(4)获得，需满足x不在前提的任何公式和B中自由出现的条件.另外，式(6)从形式上看，前提不含∃量词，结论含∃量词，与存在量词消去的含义不符.

对比式(5)和式(6)，不论从形式还是语义上看，式(5)更具有存在量词消去的含义，而成立条件(b)和(c)可以由条件(a)替代.

4 存在量词引入规则分析

4.1 不同表示形式

(1)在文献[1]中的形式

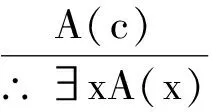
(7)

该式成立的条件是：

a.c是特定的个体常项；

b.取代c的x不能在A(c)中出现过.

(2)在文献[2]中的形式

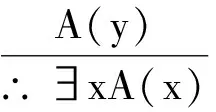
(8)

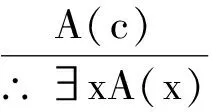
(9)

其中x,y是个体变项符号,c是个体常项符号, 且在A中y和c不在∀x和∃x辖域内自由出现.

4.2 实例比较与分析

式(7)和式(9)第一式形式相同，但成立条件的描述不同.而式(8)形式更加多样.

对式(7)，令A(c)=∃xF(x,c)，F(x,c)表示x>c，在个体域实数集中，A(c)解释为：存在实数x>c，此命题为真.而由式(7)有A(c)⟹∃xA(x)，∃xA(x)=∃x∃xF(x,x)，可解释为：存在实数x>x，此命题为假.由此在推理中出现了由真推理假的情况，推理错误.原因主要是使用式(7)时，用来替代c的x在A(c)=∃xF(x,c)中出现，因此为保证正确使用该推理规则，需满足条件(b)，即取代c的x，不能在A(c)中出现.从另一个角度看，错误的原因主要是在A(c)=∃xF(x,c)中，c在∃x的辖域中自由出现，即c在指导变元x的辖域内自由出现，因此为保证正确使用该推理规则，需满足在A中c不在∃x和∀x的辖域中自由出现的条件.

对式(8)第二式其结论进行等值演算，B→∃xA(x)⟺∃x(B→A(x))(量词辖域收缩与扩张等值式)，此式成立要求B中不含x的出现，则式(8)第二式变为：

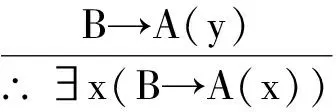
不难发现此式可由式(8)第一式推导获得，需满足B中不含x出现的条件.

再分析式(8)第一式，该推理规则形式化描述为：A(y)→∃xA(x)为永真.证明如下：A(y)→∃xA(x)⟺A(y)→∃yA(y)(换名规则)，此等值式成立要求A(x)中不含y的出现，即在A中y不在∀x和∃x的辖域中自由出现；而对于A(y)→∃yA(y)，若A(y)为真，则∃yA(y)必为真，A(y)→∃yA(y)为真；若A(y)为假，则A(y)→∃yA(y)为真.因此A(y)→∃yA(y)⟺1，即A(y)→∃xA(x)为永真，需满足在A中y不在∀x和∃x的辖域中自由出现的条件.另外对该式亦可作如下推理：A(y)⟹∀xA(x)⟹A(c)⟹∃xA(x)，推理中依次用到式(3)、式(1)第二式、式(8)(或式(9)第一式)，亦可有如下推理：A(y)⟹∀xA(x)⟹∃xA(x)，推理中依次用到式(3)和∀xA(x)⟹∃xA(x)(∀xA(x)→∃xA(x)⟺A(x)∨∃xA(x)⟺1).

最后分析式(9)第二式，对其结论进行等值演算，B→∃xA(x)⟺∃x(B→A(x))(量词辖域收缩与扩张等值式)，此式成立要求B中不含x的出现，则式(9)第二式变为

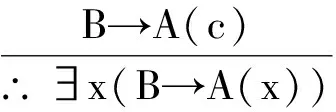
不难发现此式可由式(9)第一式获得，需满足B中不含x出现的条件.

从上分析可以看出，尽管式(8)、式(9)形式多样，但完全可以用式(7)或式(9)第一式替代.对比式(7)，式(9)第一式与其形式相同，成立条件与式(7)的条件(b)是同一问题的不同描述，即在A中c不在∀x和∃x的辖域中自由出现.

5 量词推理规则的标准形式

通过以上的分析，可以给出形式简单、直观的有关量词的推理规则，也可以给出合理、严谨的成立条件.

5.1 全称量词消去规则的标准形式

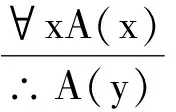
(10)

两式成立的条件是：其中x,y是个体变项符号，c是个体常项符号，且在A中x不在∀y和∃y的辖域内自由出现.

5.2 全称量词引入规则的标准形式

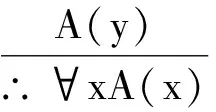
(11)

该式成立的条件是：无论A(y)中自由出现的个体变项y取何值，A(y)应该均为真.

5.3 存在量词消去规则的标准形式

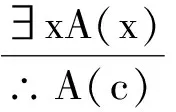
(12)

该式成立的条件是：c是使A为真的特定的个体常项.

5.4 存在量词引入规则的标准形式

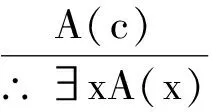
(13)

该式成立的条件是：在A中c不在∀x和∃x辖域内自由出现.

5.5 典型应用实例

例1 前提：

结论：∀x(G(x)→f(x)).

②∀x(F(x)∨H(x)), ①

③∀x(H(x)→F(x)), ②

④H(y)→F(y), 式(10)

⑤∀x(G(x)→H(x)),

⑥G(y)→H(y), 式(10)

⑦G(y)→F(y), ⑥④

⑧∀x(G(x)→F(x)). 式(11)

例2 前提：

∀x(P(x)→(Q(y)∧R(x))),∃xP(x),

结论：Q(y)∧∃x(P(x)∧R(x)).

证 ①∃xP(x),

②P(c), 式(12)

③∀x(P(x)→(Q(y)∧R(x))),

④(P(c)→(Q(y)∧R(c))), 式(10)

⑤Q(y)∧R(c), ②④

⑥Q(y),

⑦R(c),

⑧P(c)∧R(c), ②⑦

⑨∃x(P(x)∧R(x)), 式(13)

⑩Q(y)∧∃x(P(x)∧R(x)). ⑥⑨

[1] 耿素云，屈婉玲.离散数学(修订版)[M].北京：高等教育出版社，2004.

[2] 屈婉玲，耿素云，张立昂.离散数学[M].北京：高等教育出版社，2008.

[3] 耿素云，屈婉玲，王悍贫.离散数学教程[M].北京：北京大学出版社，2004.

[4] 傅 彦，顾小丰，王庆先,等.离散数学及其应用[M].北京：高等教育出版社，2007.

[5] 魏雪梅. 离散数学及其应用[M].北京：机械工业出版社，2008.

[6] 方世昌.离散数学(第三版)[M].西安：西安电子科技大学出版社，2009.

[7] 杨圣洪，张英杰，陈义明. 离散数学[M].北京：科学出版社，2011.

[8] 苑成存. 一种可行的量化逻辑自然演绎系统[J]. 洛阳大学学报，2002，17(3)：30-33.

[9] 孟令江. 一阶逻辑推理系统F下量词的性质及运算规律[J]. 河北大学学报(自然科学版)，2008，28(1)：18-21.

[10] 邱文. 一阶逻辑推理有效性的探析[J]. 海南大学学报(自然科学版)，2006，24(2):104-106.

[11] 何自强. 离散数学中与量词有关的推理规则[J]. 北京航空航天大学学报，2000，26(4)：432-434.

[12] 潘美芹，丁志军，王永丽. 谓词逻辑推理中证明方法的判定[J]. 山东科技大学学报(自然科学版)，2005，24(4)：84-86.

(编辑 HWJ)

重要启事

“优先数字出版”是以纸质版期刊录用稿件为出版内容，先于纸质期刊出版日期出版的数字期刊出版方式．我刊已于2012年起与中国学术期刊(光盘版)电子杂志社签订了优先数字出版协议．凡被我刊录用的稿件一经优先数字出版，读者即可在中国知网(CNKI)全文数据库进行检索和下载．凡向本刊投稿的作者，如无特别申明，均被视为作者授权本刊编辑部在纸质期刊出版前，可以在中国学术期刊(光盘版)电子杂志社主办的“中国知网”(www.cnki.net)上优先数字出版；也被视为作者同意并授权我刊与其他电子杂志社签订的协议，并许可其在全球范围内使用该文的信息网络传播权、数字化复制权、数字化汇编权、发行权及翻译权，并不再额外支付稿酬．

本刊编辑部

Study of Inference Rules for Quantifiers in First-order Logic Inference System

WANGWen-long1*,ZHANGBo-feng2
(1.College of Computer Science and Technology, Kashgar University, Kashgar 844000, China;2.School of Computer Engineering and Science, Shanghai University, Shanghai 200041, China)

Through the analysis of two inference rules for quantifiers and establishing conditions in first-order logic natural inference system, in this work, we establish intuitive inference rules for quantifiers with reasonable and strictly elaborated conditions. Not only these rules are intuitive and strict, but they also establish conditions that can accurately be grasped.

first order logic; universal quantifier; existential quantifier; inference rules; establish condition

2016-05-04

国家自然科学基金项目(61561027)；新疆高校科研计划重点项目(XJEDU2014I039)

10.7612/j.issn.1000-2537.2017.03.016

TP301 O141

A

1000-2537(2017)03-0089-06

*通讯作者,E-mail：wwl-yx@163.com