基于SMC的无刷直流电机的矢量控制

刘建林，罗德荣，韩 建，李良涛(1. 湖南机电职业技术学院，中国 长沙 410151；.湖南大学电气与信息工程学院，中国 长沙 41008)

基于SMC的无刷直流电机的矢量控制

刘建林1,2，罗德荣2，韩 建2，李良涛2
(1. 湖南机电职业技术学院，中国 长沙 410151；2.湖南大学电气与信息工程学院，中国 长沙 410082)

传统的无刷直流电机(Brushless DC Motor,BLDCM)的控制方式通常采用转速PI控制，转速电流PI控制等控制策略，这类控制方法简单，但同时也存在一些转速误差较大，转矩抖动明显等问题.为解决这些问题，采用矢量控制策略，并提出积分滑模算法(Sliding Mode Control,SMC)代替电流q轴分量PI调节算法.通过搭建该调速系统仿真模型及实验分析，与传统PI控制算法相比，该系统转速跟踪误差小，转矩抖动明显减小，系统动态响应快，鲁棒性强.

无刷直流电机；矢量控制；积分型滑模控制；比例积分微分控制

无刷直流电机是一种新型的由电机主体和驱动器组成的机电一体化产品.由于其良好的控制性能，较宽的调速范围，大的启动转矩以及高效率，运行平稳等优点广泛应用于汽车，工业自动化，航空航天等方面.传统的无刷直流电机一般采用PI控制，算法简单，易于控制，但缺点也很明显：噪声高，转矩脉动大，对电机控制效率不高.

近年来，包括矢量控制，直接转矩控制策略，以及模糊控制，神经网络控制，滑模控制算法在内的许多现代控制理论被逐渐应用到无刷直流电机的调速系统中.其中，滑模控制由于具有很强的鲁棒性以及对系统参数要求低等优点越来越受关注.文献[1]对永磁无刷直流电机的几种典型驱动电路拓扑结构，以及转矩脉动抑制，无位置传感器控制等进行介绍并对其发展趋势进行介绍.文献[2]在传统PID控制算法基础上设计了神经网络控制，这不仅提高了响应速度，而且提高了精度，但系统抖振问题并没有解决.文献[3]设计了永磁无刷直流电机的模糊PI控制，有效提高了响应速度和精度，却不能解决系统抖振问题.文献[4]设计了无刷直流电机的矢量控制，并搭建了Matlab仿真模型，对转速，转矩波形进行分析，发现响应速度和控制精度得到进一步提高，但是没能进行实验验证.文献[5]设计了积分滑膜变结构代替原来PID控制，使得响应速度进一步提高，并且增强系统鲁棒性.文献[6]在永磁同步电机矢量控制的基础上用积分滑膜结构代替PID控制，并设计了负载转矩观测器，能有效提高精度，加快系统响应速度，并且有效降低负载抖振问题.文献[7]设计了基于扩张状态观测器的BLDCM的滑模变结构控制，这有效抑制外界的干扰，对于系统抖振的抑制起到一定作用.文献[8]在传统直接转矩控制的基础上，设计了一种超空间矢量的DTC控制，该策略不需要检测转子位置信号，对原有系统进行极大简化.郭鸿浩等[9]设计了无刷直流电机的自适应滑模观测器，能对其反电动势进行实时估测，与之前的查表法相比更精确.史婷娜等[10]则设计了基于改进型滑模观测器的无刷直流电机的无位置传感器控制，使得系统响应速度加快，增强其鲁棒性.

为克服电机负载运行时转矩波动大，稳态控制精度不高和抖震，本文在矢量控制的基础上提出一种基于积分滑模设计的滑模控制算法，对电机的d—q轴电流调节采用PI控制算法，对电机速度调节采用滑模控制算法.通过仿真分析，这种控制算法可以更好抑制负载引起的转速波动，有效提高抗负载扰动性能.

1 无刷直流电机数学模型

现以两极三相无刷直流电机为例，直接利用电动机相变量建立数学模型.

先作以下假设：忽略空间谐波，定子三相绕组完全对称，空间互差120度，参数相同；忽略定子铁芯齿槽效应的影响；忽略功率器件导通和关断时间的影响，功率器件导通压降恒定，关断后等效电阻无穷大；忽略定子绕组电枢反应的影响，各绕组自感和互感恒定不变；电机气隙磁导均匀，忽略磁路饱和，不记磁滞损耗和涡流损耗.基于以上假设，无刷直流电机的由三相定子建立的数学模型如下：

其中ua，ub，uc分别为定子三相电压;ea，eb，ec分别为定子A，B，C三相绕组产生的梯形反电动势;ia，ib，ic分别为三相电流;R为三相绕组电阻;L为三相定子电感;M为三相绕组之间互感.

1.1BLDCM转矩方程

BLDCM运动方程为

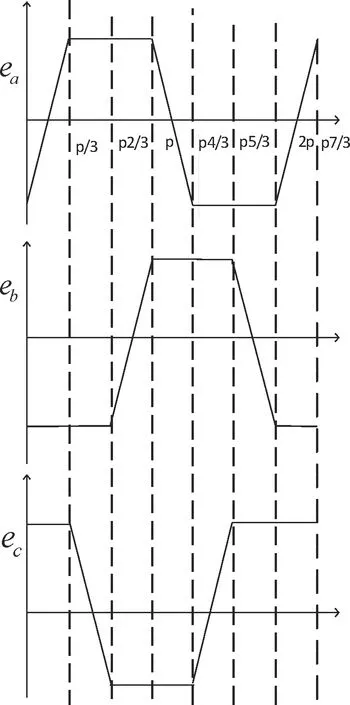
图1 三相反电动势波形 Fig.1 Three phase back EMF waveform

式中Te为无刷直流电机转矩；TL为负载转矩；w为电机机械角速度；B,J分别为电机的摩擦系数和转动惯量.

基于ABC三相静止坐标系的转矩方程为

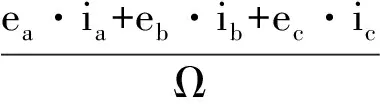
基于d-q坐标系的电磁转矩方程为

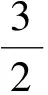
式中p为电机极对数；ed，eq分别为d-q坐标系下反电动势分量；id，iq分别为d-q坐标系下电流.取id=0，从而转矩方程为

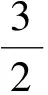
式中eq随转子位置变化而变化,从而如果提前确定转子位置,那么k(θ)便是一个定值，在某一段时间间隔内可以看做是Te与iq成线性变化，即：

Te=k(θ)·iq.

从上式可以看出，BLDCM在稳定状态下运行时，电机电磁转矩接近恒定，然而k(θ)随时间的变化而不断变化，所以iq将不再像永磁同步电机中的iq那样保持近似恒定，而是随着时间做周期性的变化.

1.2 反电动势eq与机械角速度w的关系

采用无刷直流电机为梯形波反电动势波形的BLDCM,从而可以得到三相反电动势波形.

在已知电机机械角速度w以及反电动势常数k的条件下，可由反电动势波形结合转子位置可以得到无刷直流电机每个时刻的反电动势与转速的关系.

表1 转子位置与反电动势的关系

2 积分滑模调速控制器的设计

2.1 积分型滑模面

滑模控制器的设计是依据电机实际转速w与给定转速w*的比较值u(t)进行调节，以达到误差最小化的目的.比较值为

u(t)=w*-w，

该BLDCM的状态变量可取：

式中w*为给定的期望转速；w为实际转速；u(t)为偏差量.

之前许多文献中滑模面的选取会包含速度误差与稳态误差，这一过程会带来高频噪声.在之前的基础上加入状态量的积分量，所取积分模面s为

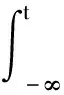
令s=0，则有u(t)′=-c·u(t)，该微分方程的解为

u(t)=c2·e-c·t.

该式表示速度误差以-c为指数趋近0.因而可以提前确定系数c来控制滑模运动的特性.在t=0时，u(0)=w*，令s=0，于是可以选取积分初始值：

上式表示系统从一开始就在滑模面上运动，于是系统便具有全局鲁棒性.

2.2BLDCM滑模结构控制率的设计

对积分滑模面切换函数s求导有：

为提高系统的动态品质，可采用如下指数趋近律

s′=-λ·sgn(s)-μ·s,

其中λ,μ均为正的常数.

从而可以得到

由于在实际的滑模变结构控制系统中存在时间延迟与空间滞后的问题，从而使得该系统存在高频抖振.本文中所用到的指数趋近律法能较好减小滑模抖振问题，因而合理设计趋近律便能解决该问题.在该系统中采用饱和函数sat(s,δ)代替符号函数sat(s)，能进一步解决抖振问题.饱和函数表达式如下：

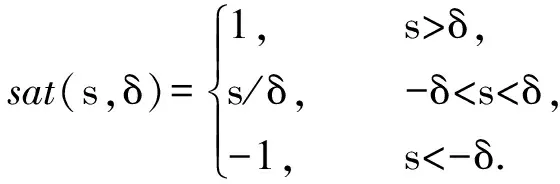
式中δ为滑模切换面的边界层厚度.

于是控制律便可表示为：

2.3 控制器的设计

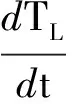
依据上式可以设计出积分滑模面控制器.

3 仿真与实验波形分析

为验证所设计控制器的合理性，通过Matlab/Simulink建立仿真模型，并以TMS320F28335为控制芯片搭建实物试验系统.调速系统采用id=0的矢量控制方案,并以积分滑模算法代替传统PI控制算法.实验所采用的BLDCM的参数见表2.

表2 无刷直流电机相关参数

3.1 BLDCM传统转速电流闭环控制

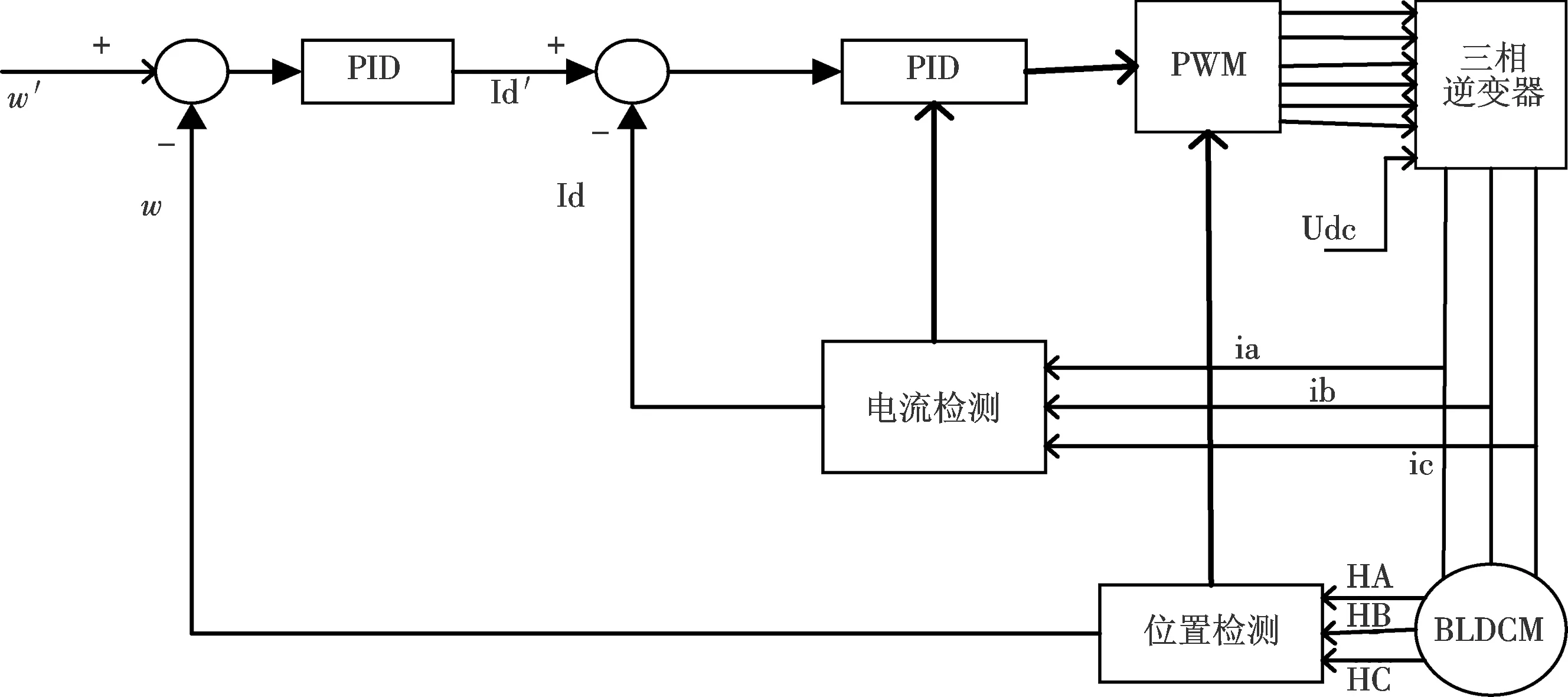
图2 传统BLDCM控制框图Fig.2 Traditional BLDCM control block diagra

图2所示为BLDCM的最常规的控制系统，采用转速及电流双闭环控制策略，控制算法为传统PID控制算法.给定转速500 rpm,负载转矩为0.8 N·m.仿真波形如图3～图6.

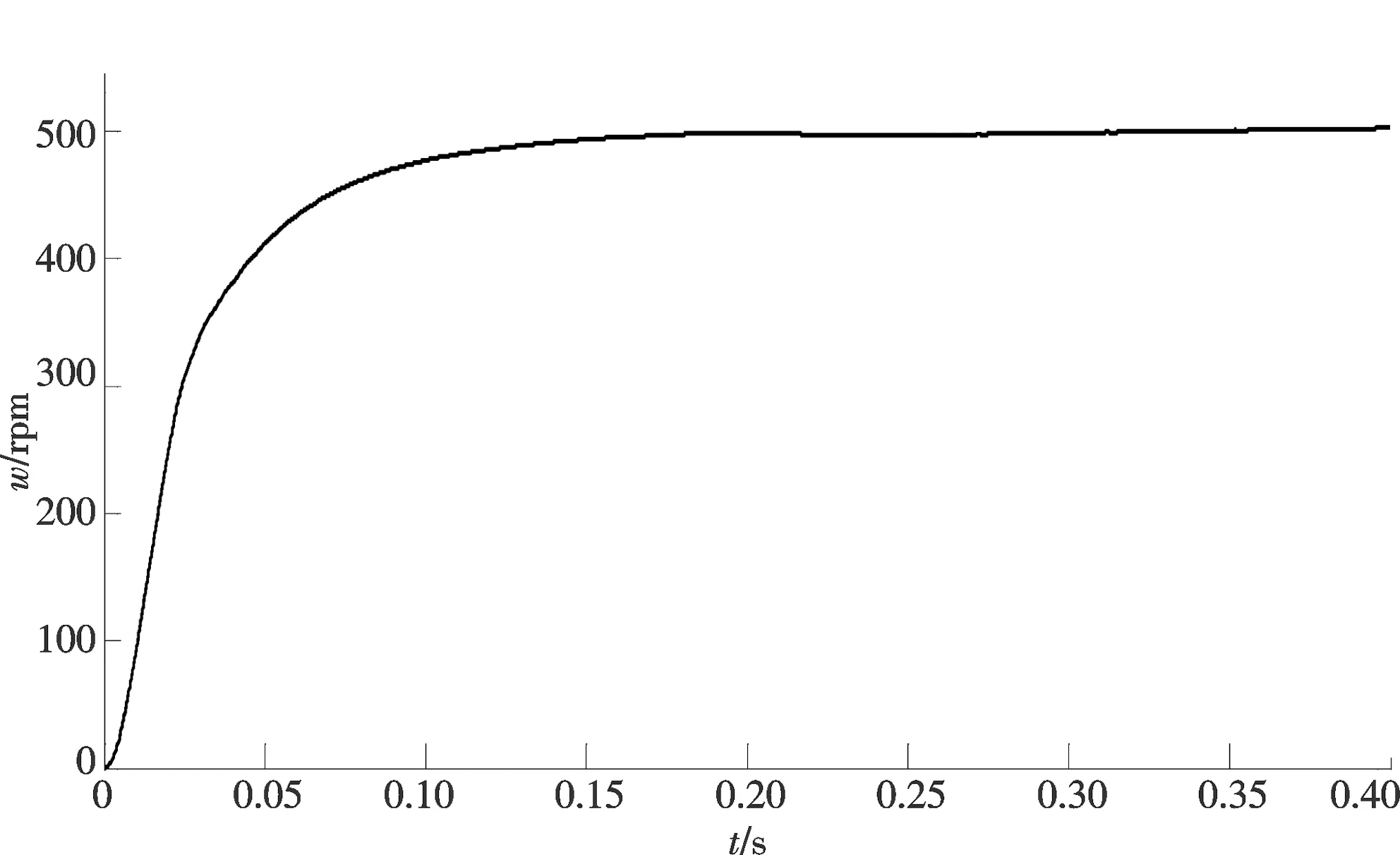
图3 常规控制方式启动波形Fig.3 Initial waveform under conventional control mode

图4 转矩突增转速变化波形Fig.4 Speed waveform changes under sudden increase of torque

图5 转矩突减转速波形变化Fig.5 Speed waveform changes under sudden decrease of torque

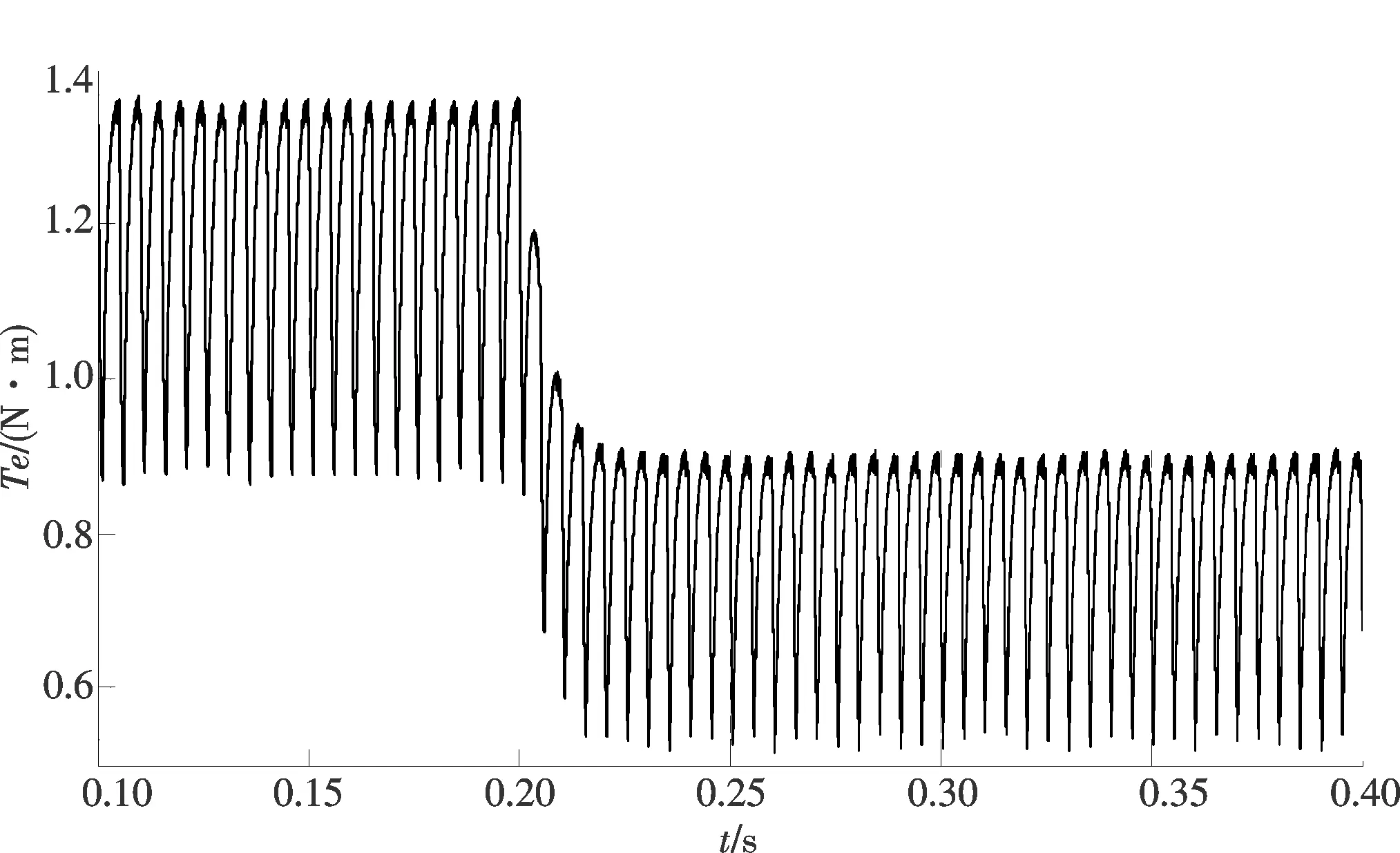
图6 转矩突减转矩波形变化Fig.6 Torque waveform changes under sudden decrease of torque

从图3～6仿真波形不难看出，在传统的BLDCM的PID转速电流闭环控制模式下，其转速及转矩抖动比较大，尤其是转矩抖动相当大，从转速波形也不难看出，系统跟踪响应速度缓慢.为此，本文提出如下BLDCM的矢量控制系统(图7).

3.2 BLDCM矢量控制

通过BLDCM的电磁转矩矢量方程可以得到如下矢量控制系统(图7)，并在原有控制系统中加入积分滑模结构.

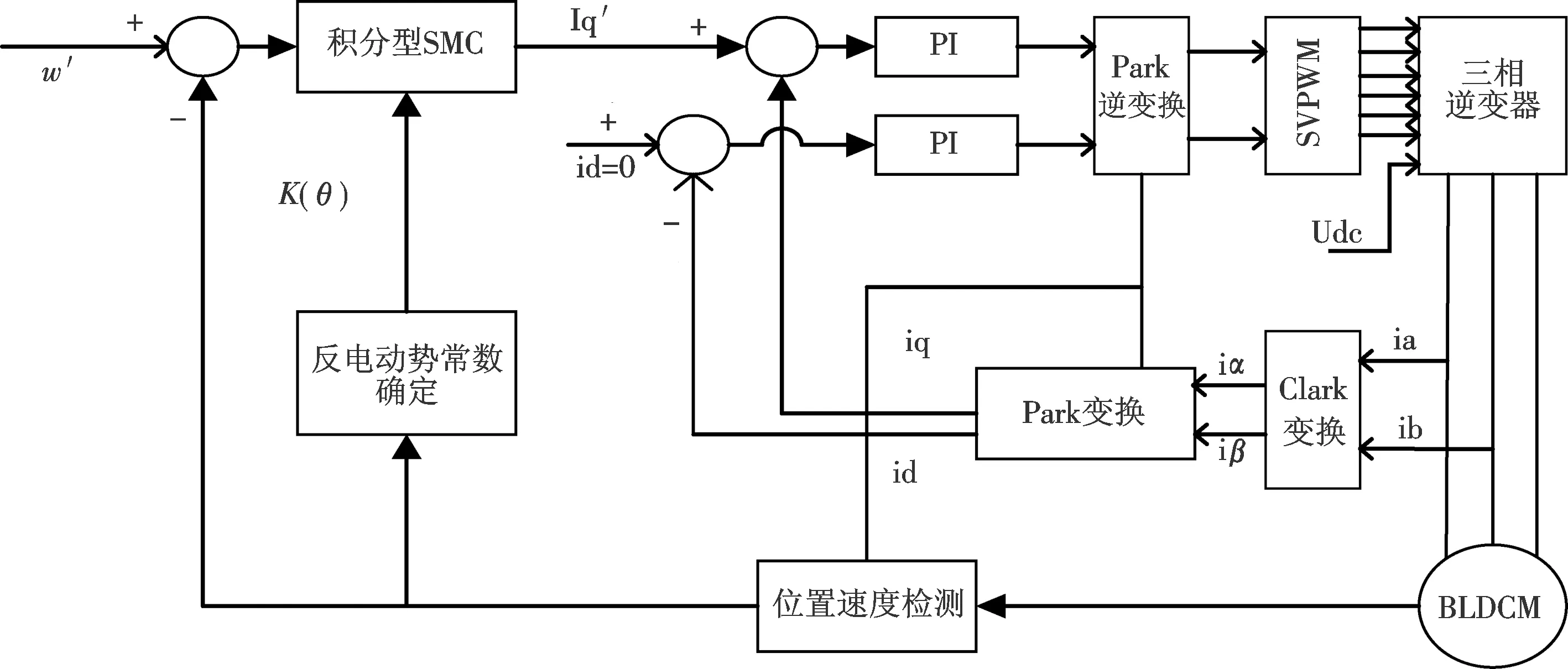
图7 BLDCM改进型矢量控制框图Fig.7 BLDCM modified vector control block diagram

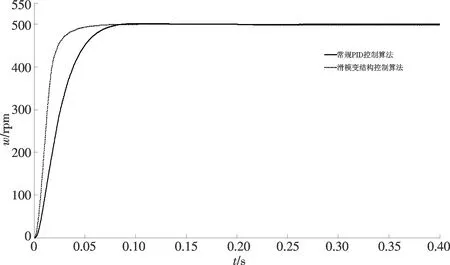
图8 启动转速波形Fig.8 Start speed waveform

图8为BLDCM在常规PI控制与积分型滑模控制条件下空载启动的波形图.从图中可以看出采用积分滑模变结构的条件下能更快到达额定转速，上升时间短，调节时间快.

图9和图10则是在负载突减的条件下转速与转矩在两种算法的条件下仿真所得的波形图.在负载转矩由1.2 N·m突减为0.8 N·m时，可以从图中看出，在SMC控制算法下，转速抖动比普通PI控制算法小，而且转速能很快稳定到额定转速(经过约75 ms恢复给定值)，能跟踪系统快速响应，调节时间快.从转矩的波形图中可以看出，SMC策略下的转矩变化更快(经过约20 ms恢复到给定值)，能快速跟踪给定信号，且误差波动更小.

图11和图12为负载突增时两种控制算法条件下的转速与转矩变化波形图.从图5中可以看出，在负载转矩由0.8 N·m突增为1.2 N·m时，SMC控制算法下的转速在0.3 s时已经稳定至额定转速，而普通PI响应速度则较慢；从图6中可以看出，在0.23 s时SMC控制算法下的转矩基本稳定为1.2 N·m，而普通PI算法下的转矩在0.28 s才稳定到1.2 N·m，且转矩抖动更小，无超调现象.说明SMC控制算法下的调速系统能快速跟踪响应，调节时间快，能有效抑制抖振.

图9 负载突减转速波形Fig.9 Speed waveform under load sudden decrease

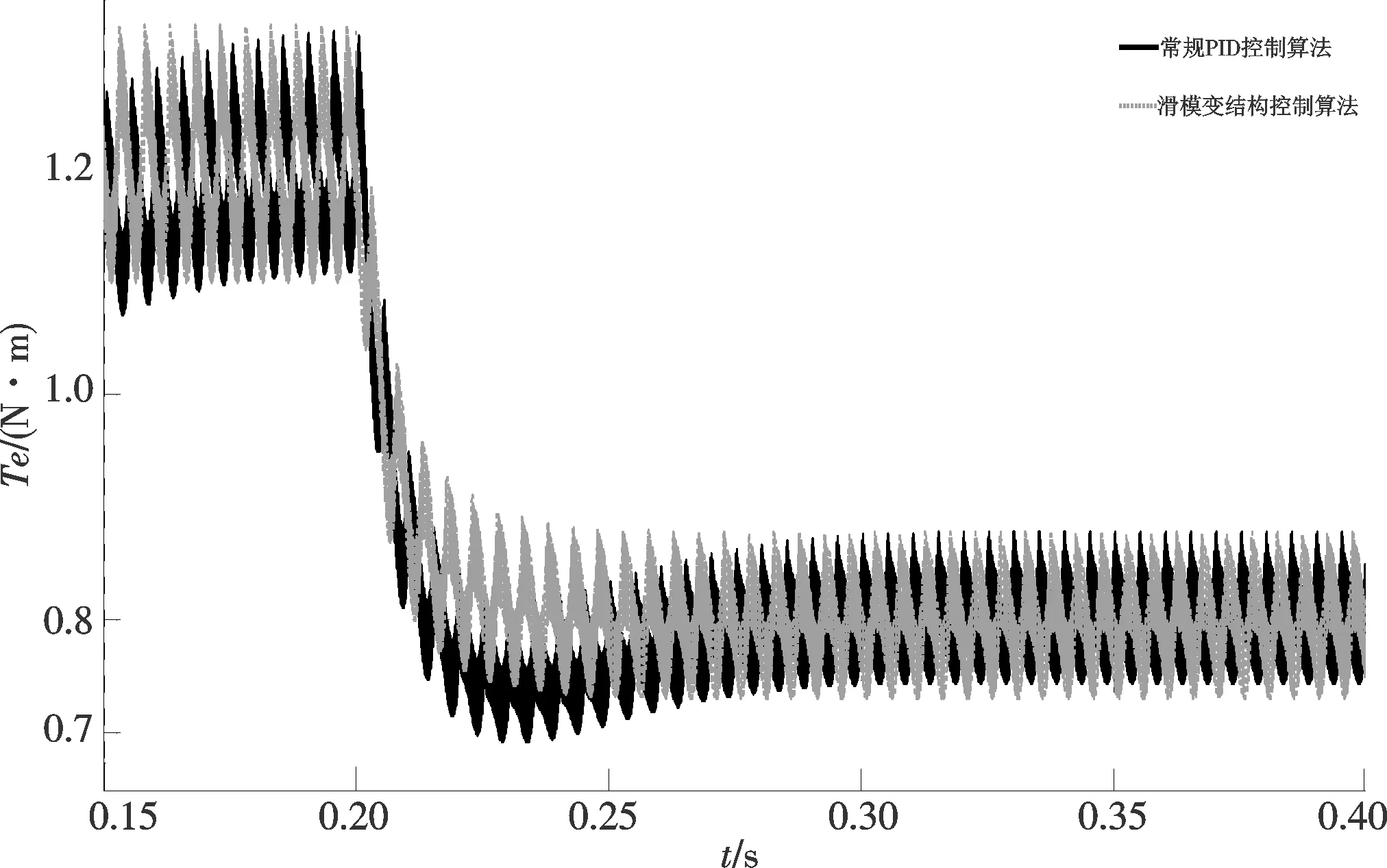
图10 负载突减转矩波形Fig.10 Torque waveform under load sudden decrease

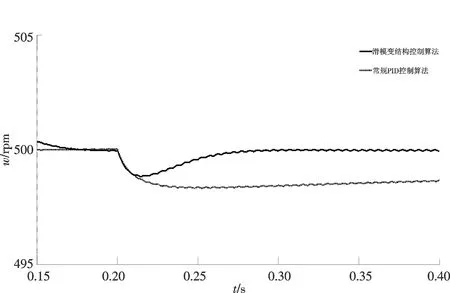
图11 负载突增转速波形Fig.11 Speed waveform under load sudden increase

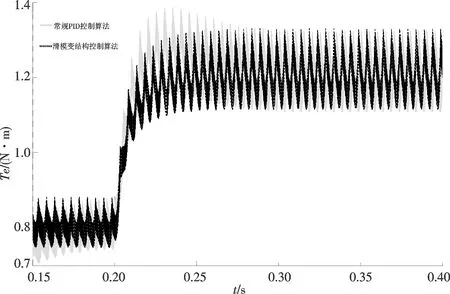
图12 负载突增转矩波形Fig.12 Torque waveform under load sudden increase

通过以上分析，可以看出该SMC算法下的控制系统对电机启动，负载突增及突减条件下能快速响应，鲁棒性好.

4 结语

为了实现无刷直流电机的较高精度控制，在以下方面做了改进，并通过实验与仿真，验证了改进方案的可行性.

通过采用传统转速控制方式与现有的矢量控制对比发现，BLDCM的矢量控制能在原来基础有效较小转矩抖动，对于电机系统稳定性的提升具有很大帮助.

采用id=0的矢量控制策略，通过对电机的转速与电流的闭环控制，能更快，更稳定调节电机的实时运行状态，具有运行平滑，启动迅速，效率高的效果.通过利用积分滑模变结构代替原有的PI控制器，能有效减小转矩抖动，增强系统稳定性，该控制器的引入使系统具有全局稳定性.

将积分滑模变结构引入无刷直流电机的矢量控制系统中，能有效提高系统稳定性.

[1] 夏长亮，方红伟.永磁无刷直流电机及其控制[J].电工技术学报,2012,27(3):25-34.

[2] 刘国海，金 鹏，魏海峰.无刷直流电机调速系统神经网络逆控制[J].电工技术学报,2010,25(8):25-30.

[3] 温嘉斌，麻宸伟.无刷直流电机模糊PI控制系统设计[J].电机与控制学报,2016,20(3):102-108.

[4] 张 鹏，贾洪平，王云财，等.模糊PI无刷直流电机矢量控制系统实现[J].机电工程,2016,33(2):202-206.

[5] 徐金龙，张向文，刘 政，等.基于积分滑模面的无刷直流电机滑模调速控制算法[J].微电机,2015,48(5):61-65.

[6] 李 政，胡广大，崔家瑞，等.永磁同步电机调速系统的积分滑模变结构控制[J].中国电机工程学报,2014,34(3)：431-437.

[7] 夏长亮，刘均华，俞 卫，等.基于扩张状态观测器的永磁无刷直流电机滑模变结构控制[J].中国电机工程学报,2006,26(20)：139-143.

[8] 高 瑾，胡育文，黄文新，等.超空间矢量下无刷直流电机的直接转矩控制[J].中国电机工程学报,2007,27(24):97-101.

[9] 郭鸿浩，周 波，左广杰，等.无刷直流电机反电动势自适应滑模观测[J].中国电机工程学报,2011,31(21)：142-149.

[10] 史婷娜，肖竹欣，肖有文，等.基于改进型滑模观测器的无刷直流电机无位置传感器控制[J].中国电机工程学报,2015，35(8)：2044-2051.

(编辑 CXM)

Vector Control of Brushless DC Motor Based on Sliding Mode Control

LIUJian-lin1,2*,LUODe-rong1,HANJian1,LILiang-tao2
(1.Hunan Mechanical and Electrical Polytechnic, Changsha 410151, China;2. College of Electrical and Information Engineering, Hunan University, Changsha 410082, China)

The control method of Brushless DC Motor (BLDCM) usually adopts the control strategy of speed PI control and speed current PI control. Such control method is simple, but there are some problems such as large error of rotational speed, obvious torque jitter and other issues. To tackle these problems, vector control strategy is used and an integral sliding-mode control algorithm(SMC) is proposed to replace the current PI control algorithm. Compared with the traditional PI control algorithm, this system has small speed error and small torque jitter. The dynamic response of the system is fast and the robustness is strong.

brushless DC motor; vector control; integral sliding mode control; proportional integral derivative(PID) control

10.7612/j.issn.1000-2537.2017.03.012

2017-03-22

国家自然科学基金资助项目 (61104088)；湖南省教育厅科技资助项目(16C0571)

TM301.2

A

1000-2537(2017)03-0064-08

*通讯作者,E-mail：tikolin@126.com