基于多目标模拟退火算法的微管网拓扑优化

李 鹏，刘 远，黄金勇

（华东交通大学机电与车辆工程学院，江西 南昌330013）

基于多目标模拟退火算法的微管网拓扑优化

李 鹏，刘 远，黄金勇

（华东交通大学机电与车辆工程学院，江西 南昌330013）

针对损伤自修复中微胶囊（或空心玻纤）载体在结构上相互独立、互不贯通等不足，研究基于多目标模拟退火算法（multiobject simulated annealing，MOSA），对微管网的拓扑结构进行优化，旨在设计一种具有低体积份数和高流动效率的，具有相互贯通结构特点的微管网载体。首先建立微管网数学模型；其次采用哈迪克罗斯迭代法设计了多目标优化函数，并结合非劣分层和MOSA算法对微管网的拓扑结构进行研究；最后与非劣分层遗传算法（non-dominated sort genetic algorithm II，NSGA-II）进行对比研究，验证了MOSA的优化性能。研究结果表明：微管网的体积份数和沿程水头损失呈负相关性；与NSGA-II相比，MOSA的收敛时长略长，但MOSA解集的支配度及分布均匀程度均优于NSGA-II。

微管网；多目标优化；模拟退火；非劣分层；哈迪克罗斯迭代

复合材料因质轻、耐磨及易加工等特点，已在航空航天、汽车、电子和建筑等领域得到了广泛应用。然而，作为一种由多种异质/异形组元材料复合而成的新材料，其力学性能分散性较大，致使材料在生产和服役中易产生各类损伤，尤其是微裂纹的产生和扩展将引起材料力学性能的劣化，导致构件过早失效。目前，复合材料的损伤修复问题已经成为结构失效与安全服役科学中的关键问题之一[1]。

上世纪80年代，美国军方首先提出了复合材料自修复的概念，其基本原理是将内置有修复剂的载体埋入材料内部，当材料受损产生裂纹时诱发载体破裂，释放修复剂，实现材料的自修复[2]。此后，美国伊利诺伊大学Carolyn Dry研究了基于空心玻纤载体的自修复体系[3]；White、Sottos和Moore等对基于微胶囊载体的自修复体系开展了大量研究，并论证了该方法的可行性[4-5]；Bond等对自修复载体的性能进行了研究[6]。在国内，哈尔滨工业大学的王荣国[7]和中山大学的章明秋[8-9]等先后也开展了基于微胶囊（或空心玻纤）载体的自修复研究；此外，本文作者也就空心玻纤载体与材料的兼容性等内容开展了研究[10]。

然而，目前自修复研究中普遍采用微胶囊和空心玻纤作为修复剂载体，由于载体彼此间互不贯通，限制了材料的损伤自修复效果（如，多次修复，修复剂更换等）。因此，研究旨在设计一种具有相互贯通结构特点的微管网载体，为保证载体与材料的兼容性和修复剂的流动效率，研究基于哈迪克罗斯迭代设计了多目标函数，并结合非劣分层和多目标模拟退火（multi-object simulated annealing，MOSA）算法，对微管网的拓扑结构进行了优化，获得了理想的结果。

1 微管网优化模型及目标函数

1.1 优化模型

研究以3×3正交微管网拓扑结构为对象，该管网由长度l为20 mm的24根管道构成9个闭环回路，各管道的内径取值为决策空间，管道编号如图1所示，其中复合材料的几何尺寸为100 mm×100 mm×4 mm，S/T分别表示修复剂入/出口[11]。

图1 正交微管网模型Fig.1 Orthogonal network model

1.2 多目标优化函数

作为损伤自修复载体，埋入材料内部的微管网要在不损坏材料初始性能的前提下，保证管道中的修复剂具有较小的沿程水头损失（即具有良好的流动效率）。因此，微管网的拓扑优化属于多目标优化问题，即

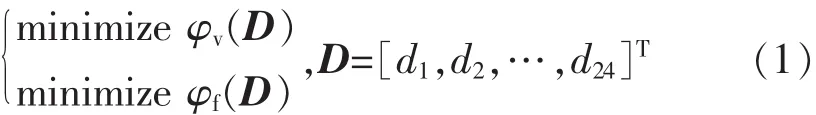
式中：φv为体积份数；φf为沿程水头损失；D为管道内径的解向量；dk为第k根管道的内径。

1）体积份数φv。微管网占复合材料的体积份数φv可表示为

式中：k为管道编号；l为管道长度；dk为第k根管道的内径；p为管道壁厚；V为复合材料体积。

2）沿程水头损失φf。修复剂流经管道的沿程水头损失表示了驱动修复剂流动所需能量的大小，为保证修复剂的流动效率，研究以全部管道的沿程水头损失之和作为目标函数：

式中：U为阻力因数；n和m为修复剂材料系数；Qk为第k根管道的流量，在忽略各环路之间相互影响的前提下，采用哈迪克罗斯（Hardy Cross）迭代方法获取各管道的流量Qk[12]。

1.3 非支配解

微管网拓扑优化的多目标函数 （即体积份数φv和沿程水头损失φf）属于非一致性优化目标，即随着体积份数下降，沿程水头损失将呈现上升趋势。因此，期望获得解空间的最优解是困难的，研究采用非劣分层方法，获取对多目标函数均有效的非支配解，即对于一个解集中任意解D1，该解集不存在解D2可同时满足① φf（D2）≤φf（D1），且 φv（D2）≤φv（D1）；② φf（D2）≤φf（D1）或 φv（D2）≤φv（D1），则该解集即为非支配解集，其中的解D1为非劣解。

图2 MOSA算法流程图Fig.2 The flow chart of MOSA

2 多目标模拟退火算法

多目标模拟退火源于对热力学中退火过程的模拟，是基于模拟退火 （simulated annealing，SA）算法，针对多目标优化的一种随机寻优算法。MOSA在搜索过程中结合逐渐趁于零且随时间变化的概率突跳，实现了全局寻优。MOSA算法包括初始解的生成、邻域解的构造和新解的产生等过程，如图2所示。

2.1 初始解集的生成

以 24根管道的内径构成解向量Di，j={dki，j}，j∈（1，2，…，800），k=1，2，…，24，其中i为迭代次数，j为当前解中解的编号，k为管道编号。研究中采用随机的方式产生规模为800的初始解集D0。

2.2 邻域解集的构造

2.3 新解集的产生及接受

新解集Di+1通过对邻域解中支配解与非支配解进行不同处理而获得，由以下两部分组成：

（2）第二部分。对于邻域解中非支配解根据式（4）计算其内能增量△E：

式中：T和T′分别为本次和上次迭代的温度值；λ为衰减因子。当内部循环次数达到链长L时，执行降温T=λT′。优化中，温度初值T0=240，衰减因子λ=0.99，链长L=10。

2.4 终止条件

优化迭代的终止条件主要由退火温度来控制，当温度达到精度要求时迭代终止。

图3 邻域解构造示意图Fig.3 Schematic diagram of constructing neighborhood

3 优化结果及分析

3.1 拓扑结构优化结果

通过MOSA算法对自修复微管网载体的拓扑结构进行优化，并获得了其迭代过程及最终非支配解，如图4和图5所示。

图4 MOSA迭代过程Fig.4 The iterative process of MOSA

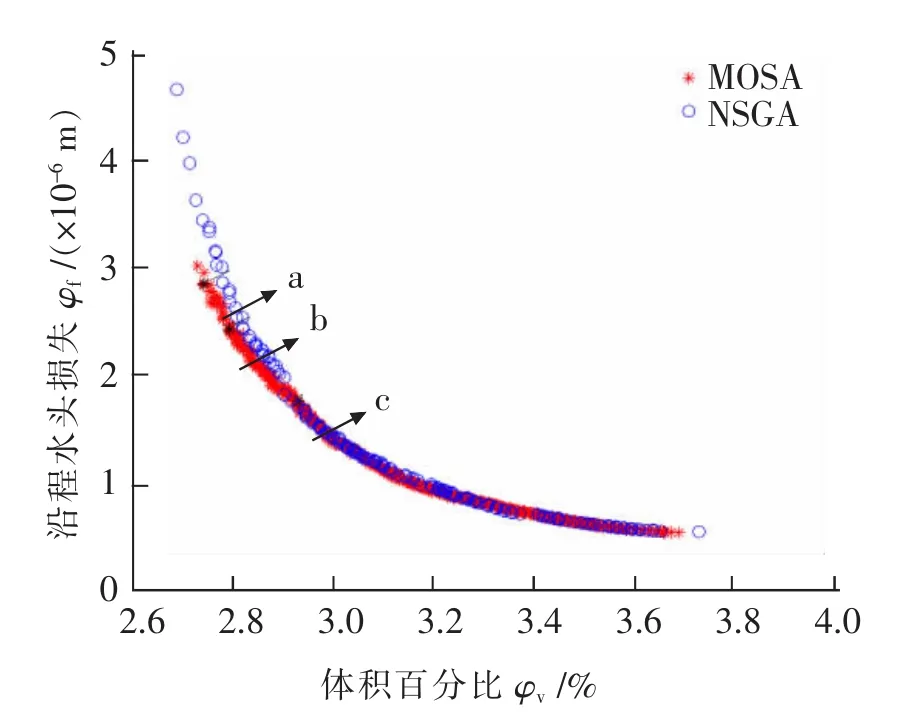
图5 MOSA和NSGA-II非支配解Fig.5 Non-dominated solution of MOSA and NSGA-II

图4中由下到上分别为MOSA第100，200，400，600，800，1 000次和1 233次迭代中的非支配解，结果表明：

1）最终收敛迭代次数为1 233；

2）随着迭代次数增加，非劣解个数由64增至190；

3）各次迭代所获得的非支配解，其体积份数与沿程水头损失均呈负相关性。

图5给出了第1 233次迭代的第一层190个非支配解，取非支配解（a），（b）和（c）进行分析，其对应的管网拓扑结构如图6所示。

图6（a），（b）和（c）分别对应于图5中（a），（b）和（c）处的非支配解，线条的粗细代表管径的大小，管道下方和左方为对应管道的直径，单位为mm。体积份数依次为2.73%，2.88%和3.25%的3个非支配解，其相应的沿程水头损失分别为2.810 6×10-6，1.601 0×10-6，7.769 0×10-6m。管网中内径较大的管道一般先从入口方向开始，并逐步向出口方向延伸，形成的大直径通道对管道中的流体起到一定的疏导作用，降低水头损失。

图6 拓扑结构优化结果Fig.6 Topology structure of optimization resuits

3.2 MOSA算法性能分析

为验证MOSA的优化性能，在相同条件下，将多目标退火算法与非劣分层遗传算法（non-dominated sorting genetic algorithm II，NSGA-II）进行了对比研究[13-14]，主要包括：① 两种算法之间非支配解的支配关系，即解的优劣；②非支配解分布的均匀程度；③ 非支配解的收敛性。

3.2.1 非支配解的支配关系

不同解集之间的支配关系是评价解集优劣的重要标准，首先采用两种算法分别获得了非支配解（如图6所示），其次，对两个解集进行非劣分层分析，并通过分析非支配解中，MOSA和NSGA-II解集所占的比例（PSA和PGA），实现两个解集整体的优劣程度的判断，对比结果表明，MOSA和NSGA-II的非支配解共有252个，其中MOSA解集190个均为非支配解，NSGA-II解集62个为非支配解，占比分别为：PSA=75.4%，PGA=24.6%，显然，采用MOSA算法获得的解集显著优于后者。

3.2.2 非支配解分布的均匀程度

非支配解分布的均匀程度表征了解集的多样性（即非劣解的选择空间）。采用平均距离对非劣解的均匀程度进行评价，计算公式如下：

式中：φl为第l个目标函数；n为非支配解的规模。平均距离越短，表明非劣解分布越均匀。结果表明：① 以φv进行评价，MOSA和NSGA-II的分布均匀程度为0.001 2和0.001 3，MOSA提高了8.3%；②以φf进行评价，MOSA和NSGA-II的分布均匀程度分别为3.102 7×10-9和 5.188 3×10-9，MOSA提高了65.3%。

3.2.3 非支配解的收敛性

图7中由下到上分别为NSGA-II第1 000，2 000，4 000，6 000，8 000，1 000次和12 000次迭代中获得的非支配解，图中X、Y轴分别为目标函数φv、φf，Z轴为迭代次数。由于MOSA存在着内部循环，其时间复杂高于NSGA-II，因此NSGA-II的迭代次数设置为12 000。非支配解个数均达到解集规模设定值800。MOSA和NSGAII的收敛时长分别为19 985 s和18 674 s，NSGA-II略优于MOSA。

图7 NSGA-II迭代过程Fig.7 The iterative process of NSGA-II

4 结束语

针对损伤自修复中微管网载体的拓扑结构优化问题，研究基于哈迪克罗斯迭代法，设计了优化目标函数，采用MOSA算法并结合非劣分层方法，研究了一种多目标微管网拓扑结构优化方法。

1）采用哈迪克罗斯迭代法，修正了微管网中各管道的流量，获得了表征微管网流动效率的沿程水头损失，并以其作为目标函数之一；

2）结合MOSA和非劣分层方法，对微管网的拓扑结构进行了优化，经1 233次迭代后，共获得190个非支配解，结果表明：体积份数与沿程水头损失呈现负相关，且管网中内径较大的管道主要沿入口方向，并逐步向出口方向延伸；

3）通过与NSGA-II的优化结果进行对比，结果表明：在NSGA-II的收敛时长略优于MOSA的情况下，MOSA的优化结果支配度75.4%优于NSGA-II的24.6%；以φv和φf进行解集分布均匀程度评价，MOSA分别提高了8.3%和65.3%。

[1]祁恒治，赵蕴慧，朱孔营，等.自修复聚合物材料的研究进展[J].化学进展，2011（12）：2560-2567.

[2]王晓岗，张星，李原芃，等.自修复功能防腐涂膜研究进展[J].功能材料，2012，43（19）：2584-2587.

[3]DRY C M.Self-repairing of composites[J].Proceeding of SPIE-the International Society for Optical Engineering，2003，5055：376-379.

[4]OLUGEBEFOLA S C，ARAGON A M，HANSEN C J，et al.Polymer microvascular network composites[J].Composite Materials，2010，44（22）：2587-2603.

[5]PATRICK J F，SOTTOS N R，WHITE S R.Microvascular based self-healing polymeric foam[J].Polymer，2012，53（19）：4231－4240.

[6]KNIPPRATH C，MC COMBE G P，TRASK R S，et al.Predicting self-healing strength recovery using a multi-objective genetic algorithm[J].Composites Science&Technology，2012，72（6）：752－759.

[7]李海燕，王荣国，刘文博，等.微胶囊自修复聚合物材料[J].宇航材料工艺，2010，40（1）：1-4.

[8]章明秋，容敏智.结构用自修复型高分子材料的制备[J].高分子学报，2012（11）：1183-1199.

[9]汪海平，容敏智，章明秋.微胶囊填充型自修复聚合物及其复合材料[J].化学进展，2010，22（12）：2397-2407.

[10]李鹏.智能复合结构损伤光修复与监测的相关技术研究[D].南京：南京航空航天大学，2009.

[11]王宪杰，张洵安.基于宏观性能的微观多孔材料拓扑优化[J].功能材料，2014，45（18）：18078－18082.

[12]丁祖荣，单雪雄，姜楫.流体力学[M].下册.北京：高等教学出版社，2003：14－19.

[13]曾毅，朱旭生，廖国勇.一种基于邻域空间的混合粒子群优化算法[J].华东交通大学学报，2013，30（3）：44-49.

[14]傅军栋，邹欢，康水华.PSO-SVM算法在智能建筑环境监控系统中的应用[J].华东交通大学学报，2016，33（1）：121-127.

Topology Optimization of Micro-vascular Network Based on Multi-objective Simulated Annealing Algorithms

Li Peng，Liu Yuan，Huang Jinyong
（School of Mechanotronics&Vehicle Engineering，East China Jiaotong University，Nanchang 330013，China）

In the self-healing research,the microcapsule（or the hollow glass giber）is served as the carrier of self-healing agent.However,this carrier has some deficiencies such as being independent and uncorrelated with each other.In this paper,a novel carrier of micro-vascular network based on multi-objective simulated annealing(MOSA)algorithms was studied and topology of micro-vascular network was optimized to design a carrier with low volume fraction,high flow efficiency and inter-connective structure.Firstly,the mathematical model was established.Secondly,the multi-objective optimization function was designed by iteration of Hardy Cross.And then the topology of micro-vascular by MOSA algorithms combined with non-dominated sorting was studied.Finally,the superiority of MOSA was verified compared with non-dominated sort genetic algorithm (NSGA-II)algorithms.The results show that volume fraction and flow efficiency of micro-vascular network are negatively correlated.The convergence time of NSGA-II is slightly better than NSGA-II,but the degree of dominant and uniformity of MOSA are significantly better than that of NSGA-II.

micro-vascular network；multi-objective optimization；simulated annealing；non-dominated sorting; iteration of Hardy Cross

TB381

A

1005-0523（2017）03-0125-06

（责任编辑 刘棉玲）

2016－12－16

国家自然科学基金项目（51365012）；研究生创新专项资金项目（YC2015-S237）

李鹏(1976—)，男，副教授，博士，研究方向为智能结构，优化算法。