模糊条件下配送中心选址评价方法研究
楼振凯,戴晓震
(温州商学院管理学院,浙江 温州 325035)
模糊条件下配送中心选址评价方法研究
楼振凯,戴晓震
(温州商学院管理学院,浙江 温州 325035)
在配送中心选址问题的背景下,从定性和定量两个角度出发分析对比已有的选址评价方法,指出其适用对象。在此基础上,结合指标对比关系的模糊性和指标数值的模糊性,对模糊条件下配送中心选址评价问题进行分类处理:模糊层次分析法确定指标对比关系模糊下的权重,并运用灰色综合评价确定评价对象的优劣性;离差最大化法求得指标数值模糊下的权重,利用改进理想解排序法(TOPSIS)对评价对象按理想程度进行排序。并结合算例说明不同情形下方法的有效性和适用性。
评价方法;模糊指标;确定权重;灰色关联度;离差最大化
作为供应商与客户的桥梁,配送中心在物流系统中起着重要的承接作用。而配送中心的选址问题则是配送中心规划与建设的关键一环,不仅决定了配送模式和配送距离,而且影响着整个系统的运作效率。关于配送中心选址的研究主要可以分为两大类:一类是以数学规划、智能算法为工具的节点寻找问题,通过建立选址模型求得理想节点;另一类是以评价模型为主的节点选择问题,运用层次分析法、熵权法、理想解法等对备选地址进行筛选排序。
关于节点寻找问题,早期的研究中常用的模型和方法有混合整数规划模型、鲍姆尔-沃尔夫法、逐次逼近模拟法等。后续的研究中,文献[1]提出了基于轴不等式族的分支割平面法,在解决无容量限制的选址问题中取得满意的效果;对于类似的问题,文献[2]改进了半拉格朗日松弛算法,通过对偶上升算法寻找原始-对偶问题最优解;文献[3]从图论的角度出发,构建了加权动态图的选址模型并通过实际案例分析了模型的合理性。然而,由于选址问题的实际约束大大多于理论约束,优化算法求得的理想解往往并不具有可行性,因此近几年学者大多从对备选节点评价、排序的角度深入研究。文献[4-9]分别从指标对比和指标数值的角度确定各指标的权重,并对指标数值进行标准化处理,从而得出每个备选节点的综合评价值;文献[10]考虑到熵权法片面地通过指标变化范围确定权重的缺点,采用三角模糊数改进并取得了良好效果;文献[11-13]分别从数据方差均值和欧氏距离的角度对灰色关联度进行改进,提出改进的灰色综合评价法解决选址问题。文献[14]将特征值法和TOPSIS结合,求得备选点的综合排序。
上述研究一定程度上解决了节点寻找和节点选择问题。然而,现有文献较少考虑到确定权重的时候指标重要性对比的模糊性以及指标数值本身的模糊性问题,而模糊性在现实问题中又普遍存在。本文在总结权重确定和备选点排序的评价方法的基础上,对两类模糊问题提出改进评价方法。对指标间对比关系模糊的问题,采用三角模糊数表示其决策矩阵,通过模糊层次分析确定权重,灰色综合评价求得备选节点的优劣排序;对指标数值模糊的问题,采用离差最大化法确定指标权重,改进TOPSIS法对备选节点进行排序。
1 指标分析和方法比较
评价指标的选取取决于对选址影响因素的分析。对影响因素分析如下:
1)客户信息分析。配送中心以提供给客户更好的配送服务作为目标,对客户信息进行分析是选址的首要任务,客户信息分析的主要指标是客户需求量以及客户地理位置。现实问题中,地理位置一般是确定的,而需求量往往是模糊性指标。
2)交通便利性分析。配送活动包括装车、运输的过程,交通便利性越强,那么道路的通行效率相对越高,越便于车辆调度。
3)土地成本分析。配送中心建设成本是企业所关心的主要问题,选址位置的不同,直接导致土地使用成本的差异。
4)政策支持度分析。配送中心的建设和发展也离不开政策的支持,故应该考虑区域产业发展的情况。当地区域对物流的支持力度越大,往往获得的优惠政策越多。
配送中心选址问题属于多属性决策问题,对多属性决策问题的评价方法进行总结和比较如表1所示。
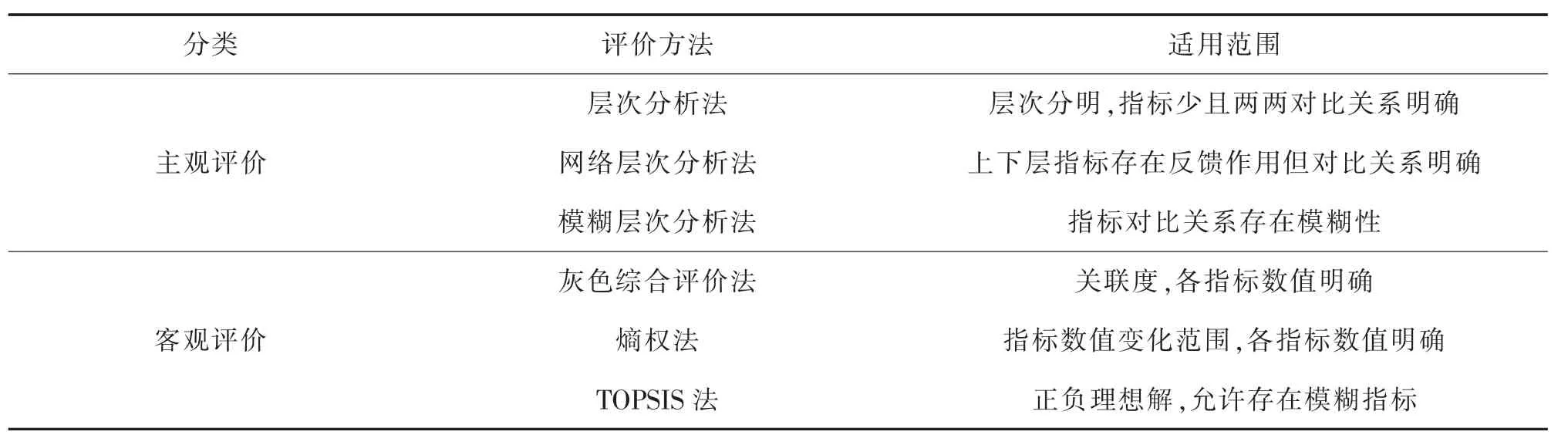
表1 评价方法比较Tab.1 Comparison of evaluation methods
在表1的方法中,各类层次分析、熵权法主要用于对指标权重的确定,灰色综合评价和TOPSIS则解决评价对象的优劣排序问题。
2 对比关系模糊性问题
指标两两对比关系模糊,但指标数值确定的问题,给出模糊层次分析法确定指标的权重,并对指标数值标准化处理,构造参考数列,求各评价指标的关联度并进行排序。
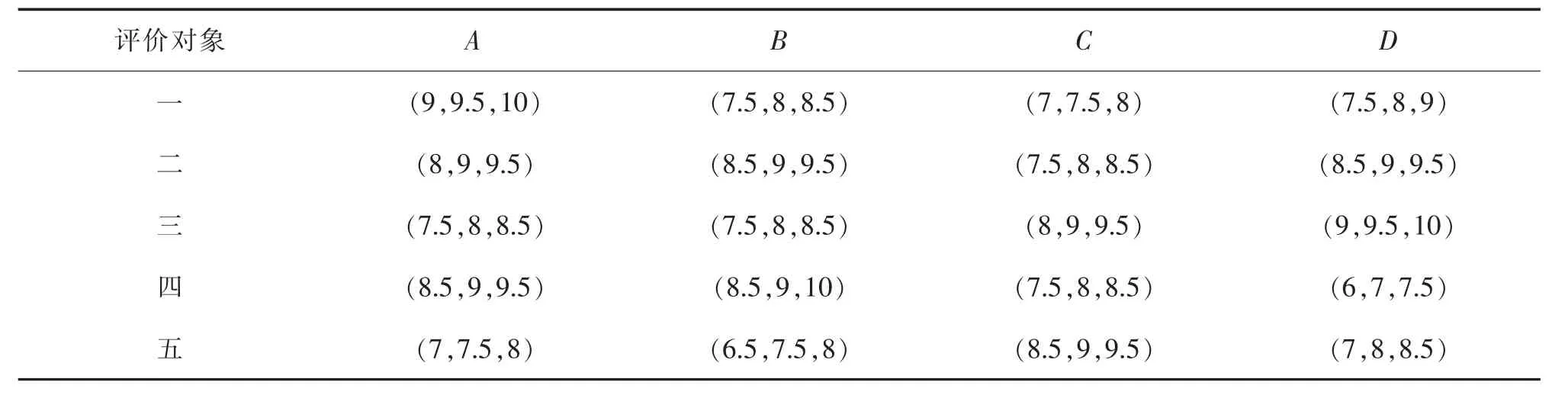
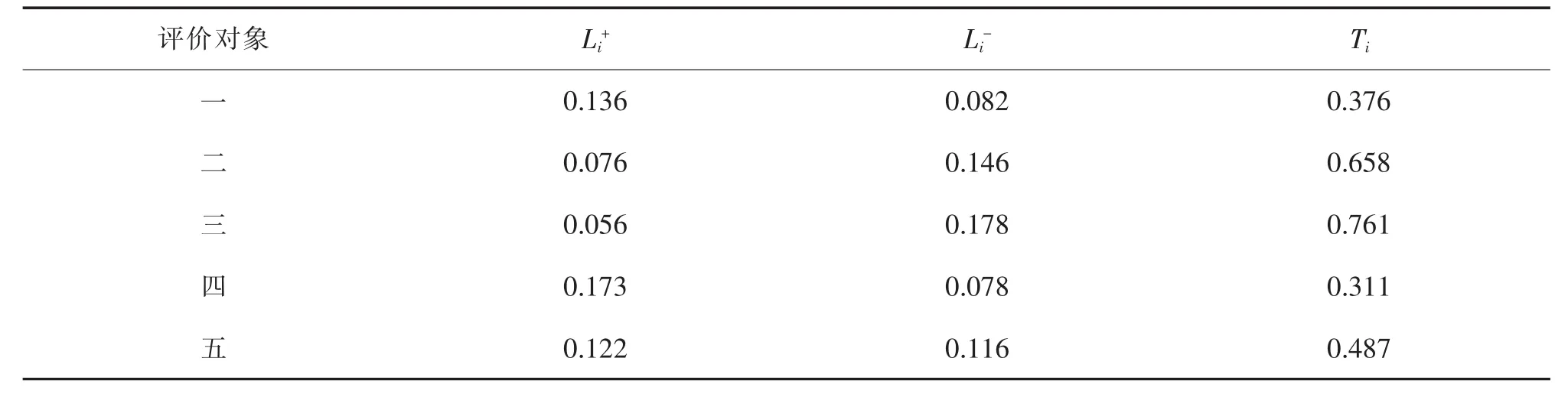
采用包括最低可能值、最可能值和最高可能值的三角模糊数作为专家评价的比较值。给出多个专家进行模糊打分情况下的模糊数整合规则。对于第i个评价对象在第j项指标上的测评值,n个专家模糊打分分别为X1=(a1,b1,c1),…,Xn=(an,bn,cn),其中ai 由介值定理可知,X仍然是一个三角模糊数。得到模糊决策矩阵A如下 式中:xmn表示整合的模糊值。计算指标i的模糊综合值pi,按以下公式 得到各指标的模糊权重,最后通过模糊隶属度函数去模糊化,并确定每个指标的权重P 将以上权重归一化,得到各指标的主观权重P=(p1,...,pn)。 灰色综合评价的第一步是对指标数值进行同趋化和标准化处理,后者也称无量纲化。对于效益型指标,将整列数值和其中最小值作比;对于成本型指标,取整列中最大值,和列中每个数值作比。灰色关联分析常用的标准化处理有初值化和均值化,考虑到计算关联度之前每个指标要乘上其权重,本文采用另一种同趋化和无量纲化同时处理的极差法,将指标数值规范在[0,1]之间。设评价指标数值矩阵Y=(yij)m×n,处理后的标准矩阵Z=(zij)m×n。 对于成本型指标 对于效益型指标 从加权标准化矩阵中选择每个指标的最优值,组成参考数列。对于参考数列z0和比较数列zi,计算各指标对应的差的绝对值,记为Δmin和Δmax,则各评价对象各指标的关联系数由以下公式确定 式中:ζ为分辨系数,根据序列的关联程度选择,一般取(0,0.5]。将每个评价对象各指标的关联系数集中为一个值,也称绝对关联度ri,一般采用求平均数的方法 与之类似,加权关联度Ri由以下公式确定 根据加权关联度大小完成评价对象的优劣排序。与理想目标的关联度越大,表示该评价对象的理想程度越高,在排序上也越优先。 很多时候指标数值无法确切给出,只能确定其范围、程度,这类问题归纳为指标数值模糊性问题,这类问题同样可以分成计算权重、评价对象排序两个步骤。对于权重的计算,同样可以通过层次分析法、模糊综合评价等求得,然而主观判断获得的比值有其难以克服的缺陷,本文结合模糊指标的特点,给出离差最大化法的权重客观求法。在方法原理上,熵权法从指标数值变化范围所反映的信息熵出发,确定各指标的权重;离差最大化法同样以指标偏差大小为依据,以拉格朗日函数求得权重。给出离差最大化法计算过程。在获得权重的情况下运用TOPSIS法计算评价对象到正负理想解的距离以及相对贴近度,并按贴近度的大小对评价对象进行优劣排序。 以三角模糊数表达指标数值,uij=(aij,bij,cij),则uij和ulj之间的欧式距离为 式中:qj为权重。运算遵循三角模糊数四则运算法则。离差最大化模型表达为 构造拉格朗日函数可求得 确定了指标权重,可以运用改进TOPSIS法对备选点排序。 步骤1:规范化决策矩阵。规范化的目的同样是为了同趋化、归一化,对正向指标和负向指标分开处理。对于三角模糊数,当指标属于正向指标时 当指标为负向指标时 式中:λmaxj为每个指标的最大值;μminj为每个指标的最小值。 步骤2:确定加权规范化决策矩阵W 步骤3:确定正理想解I+和负理想解I-,其中模糊数的比较采用均值法 步骤4:计算第i个评价对象到正负理想解的欧式距离 步骤5:计算每个评价对象与理想目标的相对贴近度Ti 4.1 算例1 某地计划新建一个配送中心,现有五个备选地址可供选择,考虑的指标为土地成本、需求量、交通便利性和政策支持度等,这其中有准确数值、评分、百分比等,记为A,B,C,D。数据见下表。 表2 评价原始数据Tab.2 Original evaluation data 标准化数据之前,先确定各指标权重。利用三角模糊数来表达决策偏好。三位专家的打分表如下。 表3 模糊判断矩阵Tab.3 Fuzzy judgment matrix 各指标权重P=(0.22,0.29,0.11,0.38)。标准化矩阵如表4所示,其中零为参考项。 表4 标准化矩阵Tab.4 Standardized matrix 求得各备选点的加权关联度为(0.465,0.670,0.707,0.570,0.635)。可以看出,各备选地址的优劣顺序为三,二,五,四,一。 4.2 算例2 同样有5个备选地址,考虑的指标为土地成本、需求量、交通便利性和政策支持度。现实问题中,在投入运营之前无论哪个指标都无法给出确切数值,只能给出程度范围,存在语言值向数值转化的过程。因此用模糊性指标表达较符合实际,本文采用三角模糊数。基于偏好信息的专家打分如表5所示。 表5 模糊判断矩阵Tab.5 Fuzzy judgment matrix 离差最大化法求得权重Q=(0.25,0.23,0.19,0.33),标准化处理后的加权决策矩阵如表6所示。 表6 加权决策矩阵Tab.6 Weighted decision matrix 由式(17),式(18)可得正负理想解为 由式(19),式(20)以及正负理想解计算各备选地址到正负理想解的欧式距离及相对贴近度,数据见表7所示。 表7 相关距离及贴近度Tab.7 Correlation distance and closeness degree 由理想解法贴近度大小排序知,备选地址的优劣排序为三,二,五,一,四。 配送中心选址的优劣对企业物流系统运作成本、效率有着深远影响,而基于优化算法的节点寻找往往不能满足实际问题的诸多定性约束。对备选地址进行分析、比较和评估,从中选择最理想的地址作为配送中心的节点选择问题引起更多关注和研究。 选址评价问题中,往往存在模糊性因素。本文将模糊选址评价问题分为两类,即指标对比关系模糊性问题和指标数值模糊性问题,分别给出模糊层次分析法-灰色综合评价法和离差最大化法-TOPSIS法,对两类问题提供了可行的解决方法。算例分析表明,改进的评价方法具有可行性和适用性。文章的不足之处在于,没有对主观评价和客观评价的优劣程度给出评判准则,后续的研究还可以对主客观权重的平衡、指标数较多且相互关联的问题展开研究。 [1]安邦,程朋.基于分支割平面的一类无容量限制设施选址问题求解算法[J].运筹学学报,2015,19(4):1-13. [2]张慧珍,魏欣,马良.求解无容量设施选址问题的半拉格朗日松弛新方法[J].运筹学学报,2015,19(4):37-47. [3]刘欣.物流园区选址模型中的动态Voronoi图问题及评价[J].价值工程,2015(21):168-169. [4]王晓博,李一军.电子商务环境下物流配送中心选址模型与评价方法[J].系统管理学报,2006,15(3):199-204. [5]许德刚,肖人彬.基于智能优化的粮食物流中心选址评价体系[J].河南工业大学学报,2009,30(6):80-83. [6]刘谡汾,马斌.煤炭物流园区多目标动态选址[J].工业工程,2015,18(6):110-115. [7]孔令明,王云峰.基于可拓层次分析法的物流中心选址评价[J].技术经济与管理研究,2009(6):25-27. [8]田时中,赵鹏大.中部六省雾霾压力动态综合评价模型与实证[J].统计与信息论坛,2016,31(9):56-61. [9]王海滨,陈延君.物流配送中心选址的熵权法综合评价研究[J].哈尔滨商业大学学报,2010(4):61-64. [10]迟国泰,王钰娟,刘艳萍.基于三角模糊熵的经济评价模型及副省级城市的实证研究[J].运筹与管理,2010,19(5):107-117. [11]陈战波,黄小舟.物流配送中心选址的改进灰关联度评价方法[J].统计与决策,2015(3):52-55. [12]朱清香,曹秋芳,刘晶.基于改进灰色关联的商业网点最优选址研究[J].统计与决策,2016(8):51-53. [13]DYMOVA,PAVEL S,ANNA T.An approach to generalization of fuzzy TOPSIS method[J].Information Science,2013(238):149-162. [14]杨磊,黄晓燕.物流配送中心选址的设计及评价模型[J].统计与决策,2008(9):80-81. [15]赵万华.区域物流配送中心选址的评价方法研究[D].武汉:武汉大学,2011. [16]王森,魏旭颖.基于模糊模型的网络社会场系统的安全评估[J].华东交通大学学报,2016,33(5):132-138. Study on Evaluation Methods of Distribution Center Location under Fuzzy Condition Lou Zhenkai,Dai Xiaozhen Aiming at the distribution center location,this paper compared the existing location evaluation methods and discussed their applications from the two perspectives of qualitative and quantitative analysis.Combining the fuzziness of the indexes contrast relationship with the fuzziness of the indexes value,it classified and solved the evaluation problems of distribution center location under fuzzy conditions:fuzzy analytic hierarchy process was used to determine the weight of indexes for the fuzzy contrast relationship,and the grey comprehensive evaluation was applied to determine the superiority and inferiority of evaluated objects;the weights of fuzzy indexes was obtained by maximizing deviations,and improved TOPSIS method was adopted to rank the evaluated objects according to the ideal level.Finally,it illustrated the effectiveness and applicability of the evaluation methods under different circumstances through numerical examples. evaluation method;fuzzy index;weight decision;grey correlation degree;maximizing deviations F252 A 1005-0523(2017)03-0081-07 (责任编辑 姜红贵) 2016-12-01 楼振凯(1989—),助教,硕士,主要研究方向为物流管理。








3 指标数值模糊性问题



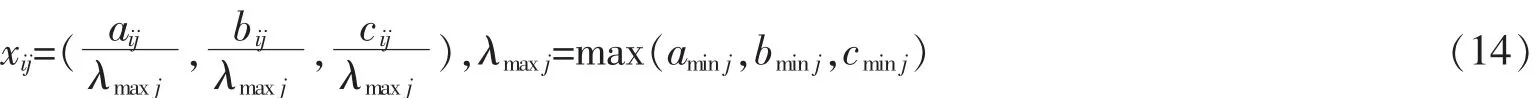
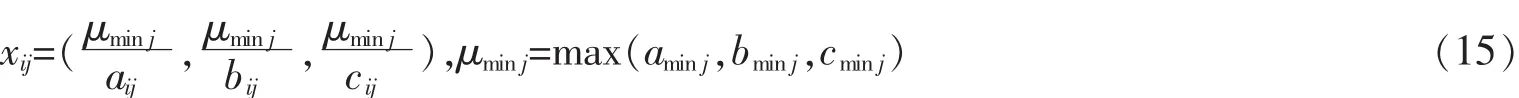




4 算例分析




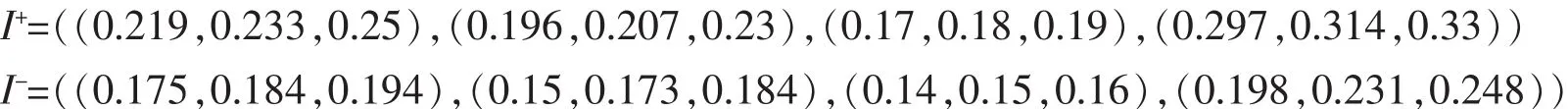
5 总结
(School of Management,Wenzhou Business College,Wenzhou 325035,China)

