基于一种新混合群算法(MOHO-SA)的结构主动控制多目标优化研究

潘兆东，谭平，周福霖,2

(1.湖南大学 土木工程学院，湖南 长沙 410082；2. 广州大学 工程抗震研究中心，广东 广州 510405)



基于一种新混合群算法(MOHO-SA)的结构主动控制多目标优化研究

基于粒子群(PSO)算法和差分进化(DE)算法提出了一种新的多目标混合群优化算法，对结构主动控制系统的作动器位置、数量与控制器参数进行同步优化.首先，分别采用PSO算法与DE算法进行对应种群的进化，使用庄家法则构造非支配解集，并引入边界点几何中心leader选择机制，同时利用模拟退火算法完成个体进化的二级局部搜索；以随机地震激励下反映结构振动控制效果和控制策略优劣的双指标作为优化目标函数.最后，针对ASCE 9层benchmark模型，采用本文提出的具有二级搜索功能的多目标混合群算法(MOHO-SA)对其主动控制系统进行优化设计，并分别与多目标差分进化算法(MODE)、多目标粒子群算法(MOPSO)、普通多目标混合群算法(MOHA)的优化结果进行对比分析，表明其Pareto解集具有更优的收敛曲线及分布性.

主动控制；混合群算法；二级搜索；多目标优化；庄家法则；几何中心leader

在土木工程结构主动控制研究领域中，作动器数量、位置及控制器参数的优化一直是研究热点之一.面对规模宏大、结构复杂、功能多样的超限工程结构，振动控制系统若采用传统的优化方法进行设计必然很难得到最优解.随机类搜索方法如模拟退火法(SA)、遗传算法(GA)及群算法为全局优化算法且可用于离散优化问题，因而被广泛地用于控制装置的位置优化研究[1-10].但以往的研究多是基于特定的外界激励、优化准则及单一优化目标进行优化设计，优化方法不具备普遍适用性，优化结果也往往只是次优解.文献[11]在限定作动器数量的前提下，利用多目标遗传算法对一6层平面框架进行了作动器位置与控制器的一体化设计，同时得到多组相对较优解.但文献[12]指出NSGA-II算法会存在收敛慢和局部搜索能力不足的问题，还有待结合具体问题的特点加以改进.

本文提出一种新的多目标混合群优化算法，同时采用粒子群(PSO)算法[13]与差分进化(DE)算法[14]进行对应种群的进化，使用庄家法则构造[15]非支配解集，并利用模拟退火算法[16]完成个体进化的二级局部搜索；文中结合土木工程结构控制特点(有较好的控制效果)及实现性(较低的控制能量)，建立边界点几何中心leader选择机制，在满足种群进化多样性要求的同时保证了收敛速度;在平稳随机地震激励下，以反映结构振动控制效果和控制策略优劣的双指标作为优化目标函数对控制系统的作动器位置、数量与控制器参数进行同步优化.最后，以ASCE 9层benchmark模型为例进行优化设计，结果表明，所提出的新混合群算法能有效地解决主动控制系统优化问题.

1 主动控制结构随机响应求解

在地震激励作用下，n层建筑的状态方程为：

(1)

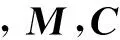
Yw=Cwzw

(2)

合并式(1)和式(2)，得到扩展的状态方程：

yT=CTzT+FTw0+DTuc

ym=CmzT+Fmw0+Dmuc

(3)

本文选用LQG控制器来设计最优反馈增益矩阵GT，结构控制力uc=GTzT.

(4)

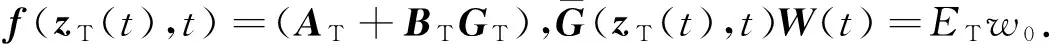
(5)

(6)

求解式(6)可得到受控结构的方差响应.

结构的状态响应根据Kalman滤波器估计获得：

(7)

式中：Le为卡尔曼滤波增益矩阵，ze为状态zT的估计值.

2 优化目标选择

考虑到控制策略的可实现性，本文以作动器允许出力均方值上限(σFallow)为多目标优化的约束条件，以结构减震效果(层间位移)和控制策略优劣(作动器出力、数量与位置)为优化目标定义如下指标：

(8)

3 混合群多目标优化算法

本文采用多目标混合群算法同时优化作动器位置、数量与控制器参数.该多目标优化问题可以表示为:

V-minJ(X)=(J1(X),J2(X))

(9)

式中:X表示决策变量(在这里表示作动器的位置、数量和控制器的设计参数)；V-min表示向量极小化，即向量J(X)中的各个子目标函数都尽可能的小.

3.1 基于庄家法则构造Pareto最优解

研究如何构造一个多目标优化问题的Pareto最优解集，实际上就是研究如何构造进化群体的非支配集，因而构造非支配集的效率将直接影响算法的运行效率.庄家法则是构造非支配集的常用方法之一，该方法具有速度快、效率高的特点，其本质上是一种非回溯的方法．使用这种方法，在每次构造新的非支配个体时不需要与已有的非支配个体进行比较，每一轮比较在构造集中选出一个个体出任庄家(一般为当前构造集的第一个个体)，由庄家依次与构造集中的其它个体进行比较，并将庄家所支配的个体淘汰出局；一轮比较后，若庄家个体不被任何其它个体所支配，则庄家个体即为非支配个体，否则庄家个体在该轮比较结束时也被淘汰出局.按照这种方法进行下一轮比较，直至构造集为空.

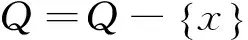
3.2 最优解边界点几何中心leader选择策略

作为多目标离散算法,多目标混合群算法会在迭代优化的过程中形成多个非支配解,这便出现了如何在种群个体更新或变异时进行leader选择的问题.结合土木工程结构控制特点(有较好的控制效果)及实现性(较低的控制能量)，并充分考虑保证群体进化的多样性，本文提出一种在进化过程中基于非支配解集边界点几何中心leader选择策略(如图1所示)，选取相对于假定非支配解集目标中心解(即非支配解集边界点确定的几何中心)距离最近的解为leader.当存在多个候选leader时从中随机选取一个作为当前leader.

图1 基于边界点几何中心的leader选择机制

3.3 混合群算法进化策略

进化策略是任何基于种群算法的关键环节，在进化过程中，种群中的个体通过不断的更新和选择，直到达到终止准则，本文采用两种进化策略：差分进化算法和粒子群算法.其中，关于作动器位置和数量的种群个体更新采用粒子群算法，而控制器参数的种群个体位置进化则采取差分进化算法.

标准粒子群粒子飞行速度与位置更新公式为[13]：

(10)

标准差分进化算法个体变异公式[14]为：

(11)

由于在一般的全局优化算法中，总希望前期有较高的全局搜索能力以找到合适的种子，而在后期有较高的开发能力，以加快收敛速度，因此，在粒子群算法的速度更新公式中引入优化过程动态变化(线性递减策略)的惯性权重[17]w；同时,对式(10)加入速度控制因子.

(12)

r=0.8×(1-0.5)k/kmax

式中：kmax为最大迭代次数.

同样，为了加快差分进化算法的收敛速度，借鉴当前种群中最好的个体信息，将式(11)修正为

(13)

3.4 模拟退火二级局部搜索

文献[11]研究表明，当控制效果降低到某一范围之内时，作动器的最优位置基本不变，此时，主动控制效果仅与控制增益有关．因此本文在优化过程中针对每一次个体变异、交叉后的位置(即控制器参数)进行一次局部随机搜索,通过全局和局部相结合的二级搜索，可以避免由于种群个体敏感度不同而引起的搜索振荡，从而优化Pareto解集的搜索.这里采用基于固体退火原理和概率理论的模拟退火算法[16]，其将优化问题类比为退火过程中能量的最低状态,也就是温度达到最低点时，概率分布中具有最大概率(概率1)的状态.本文所采用的模拟退火算法相关参数的计算公式如下：

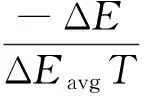
(14)

式(14)为修正的Boltzmann接受概率计算公式，ΔE表示优化目标差.

模拟降温方式：

(15)

式中：Ts和Tf分别为模拟退火过程的初始温度和终止温度；Ps和Pf为初始和终止温度可能接受较坏结果的概率；N为周期总数；Tn+1和Tn为下一时刻与当前时刻的模拟温度.

图2即为引入局部模拟退火搜索算法后的多目标混合群优化算法流程图.

4 混合群多目标优化算法

选取ASCE设计的9层钢结构Benchmark模型[18](图3)作为仿真算例.采用静力凝聚法对原有限元模型进行降阶后仅保留9个平动自由度.每一层作动器数量少于结构跨数的2/3，单个作动器最大允许控制力均方值为1 000kN，控制器权矩阵Q=10αI18×18，R=INa×Na.地震激励参数[19]：S0=3.23 cm2/s3，wg=17.95rad/s，ξg=0.64.多目标混合群优化算法参数见表1.

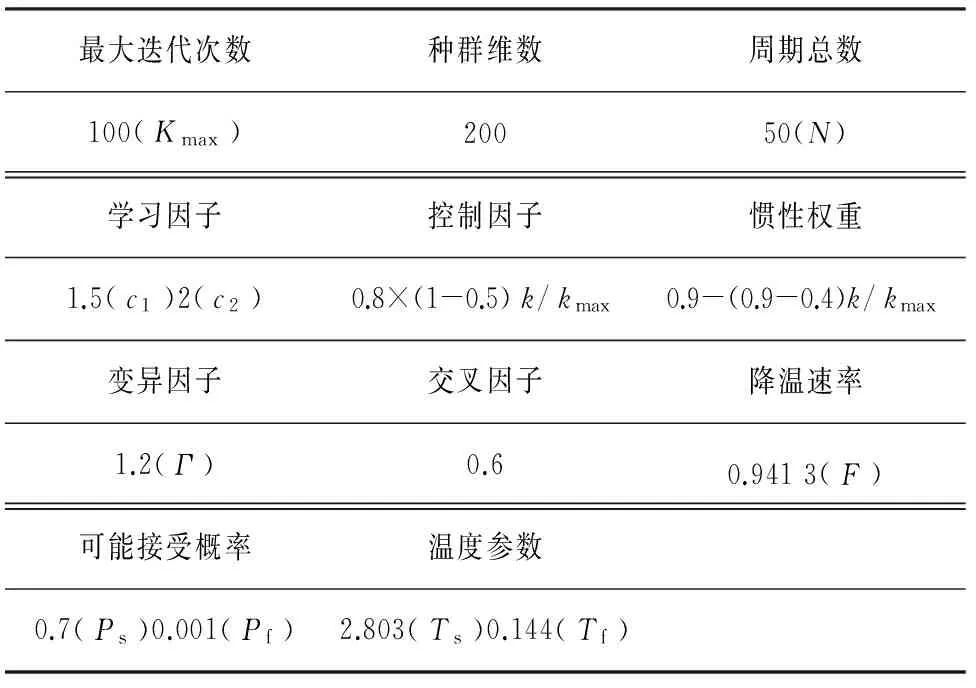
表1 MOHO-SA算法参数

图2 MOHO-SA优化流程图

图3 9层基准建筑物立面

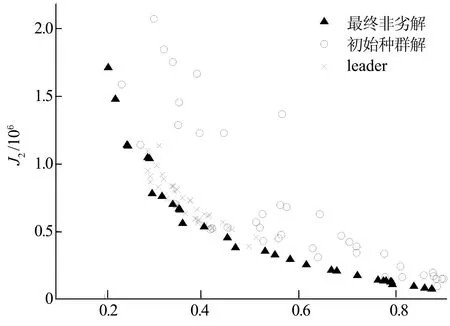
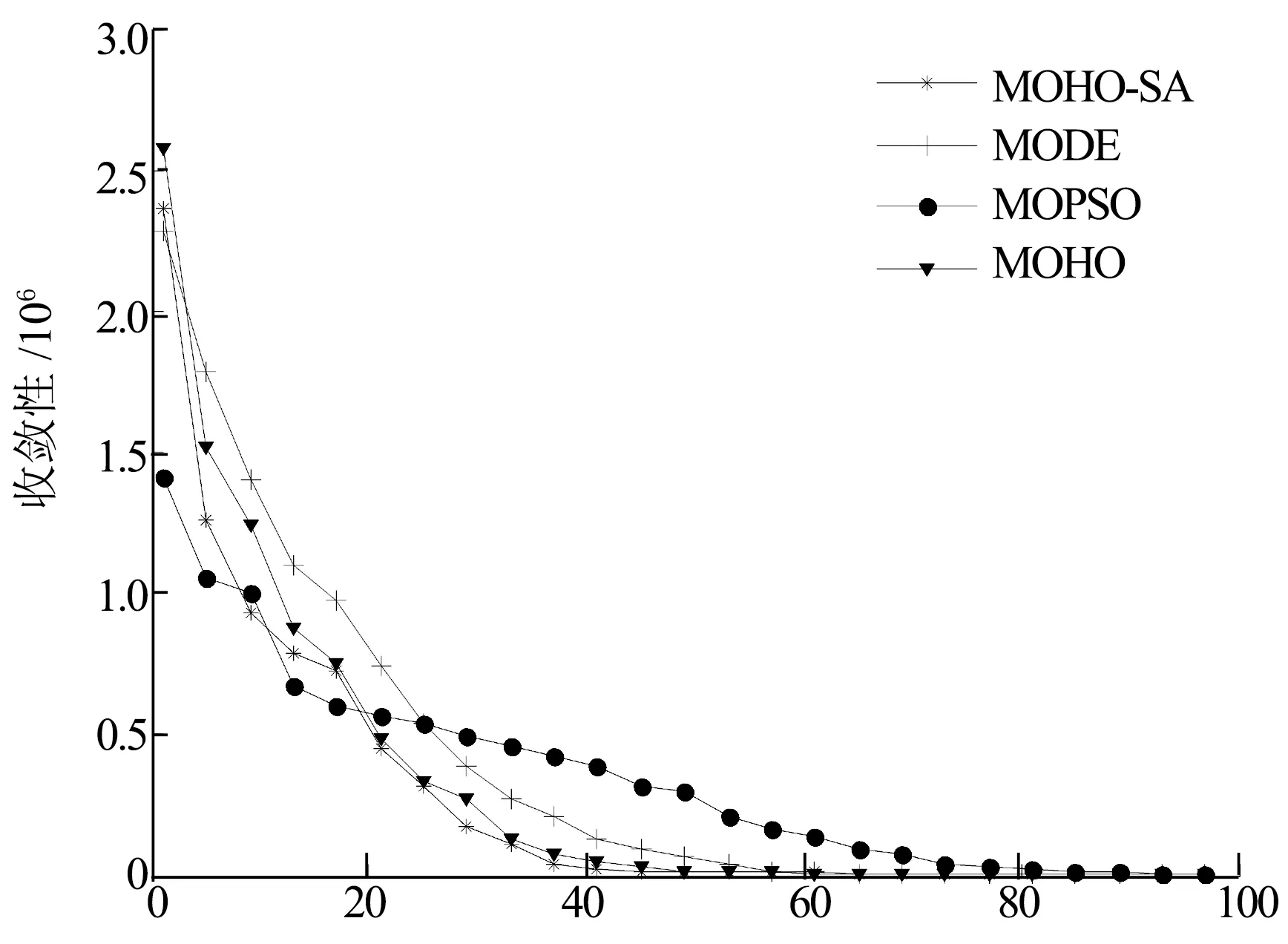
图4为利用MODE方法进行优化时获得的初始种群解、最终非劣解以及整个优化过程中选择的所有leader.可以看出，依据本文提出的边界点几何中心leader选择机制所确定的leader能很好地覆盖结构振动控制策略感兴趣的范围，不会产生过多的不可实现解(J1无限趋于小值)和无意义解(J1无限趋于1)，其在满足了种群进化多样性要求的同时也加快了收敛速度.图5给出了采用不同优化算法时的收敛曲线对比(为了便于比较，仅绘出保证曲线趋向的部分点)，图中横坐标为进化代数，纵坐标为代表收敛性的控制力方差值.可以看出，具有二级搜索功能的新混合群算法较早地进行了局部搜索，相较其他3种算法，具有更好的稳定性和收敛性.

为了说明混合群算法的优越性，在同一初始种群下，本文同时将一般多目标混合群算法(MOHO)、多目标粒子群算法(MOPSO)及多目标差分进化算法(MODE)应用于该模型控制系统的优化设计中，图6为以上3种多目标算法的最终非劣解集.由结果可知：MODE算法与MOPSO算法均会不同程度地遗失最优解，而基于双进化策略的MOHO算法最优解集则表现出很好的连续性和分布性；注意到，虽然MODE算法解集分布过于分散，但在等幅最大控制力均方差总和下(J2)，其部分解对应的(J1)较MOHO算法更小，这说明MOHO算法局部搜索能力仍然不够，因此，有必要引入二级搜索功能以加强其搜索能力.

J1

代数

J1

图7为引入局部模拟退火搜索算法后多目标混合群优化算法(MOHO-SA)获得的控制系统最终非劣解集曲线，为了便于比较，这里仅绘出最终最优解集维数的一半.将其与MOHO最终非劣解集曲线对比，不难发现，在相同优化目标J2下，MOHO-SA算法可以获得更好的控制效果(J1较小)，使控制策略进一步趋于优化.表2列出了从Pareto最优前沿曲线中选择的一些最优个体所对应的控制装置数量、位置和相应的控制器参数.可以发现，四组优化结果的作动器总数大致相同，作动器的位置也主要集中在结构中下层；其中，控制策略1可以更高效地发挥所有作动器的作用.

J1

各楼层布置作动器数量123456789J1J2/kNα13211200000.231497.6513.6823131100000.37601.6412.5733110111000.45384.5312.2443000121010.64223.2811.55

仿真分析结果充分验证了本文所提出的具有二级搜索功能的新混合群算法的正确性与优越性.究其原因，首先MOHO-SA算法在迭代过程中引入了边界点几何中心leader机制改善解集的分布性；其次进化过程中采用两种不同进化策略，并在MOHO算法基础上利用模拟退火算法加入局部二级搜索功能，从而改善了非劣解集最优前沿曲线的分布.

5 结 论

1)本文基于粒子群(PSO)算法和差分进化(DE)算法提出的多目标混合群算法能有效地解决主动控制系统作动器数量、位置及控制器参数的同步优化问题，验证了本文所提出边界点几何中心leader选择机制的实用性．

2)对于主动控制系统，一般混合群算法较单一进化策略的多目标优化算法而言，其最优解前沿线具有更好的连续性和分布性，保证了针对每一设计性能要求都有对应解，便于设计者选择．

3)具有二级搜索功能的新多目标混合群算法有效地改善了传统多目标优化算法局部搜索能力不强的缺陷，可以获得更加合理的控制策略.

[1] 刘福强,张令弥.作动器/传感器优化配置的研究进展[J].力学进展,2000,30(4):506-516.

LIU Fuqiang, ZHANG Lingmi. Advances in optimal placement of actuators and sensors[J]. Advances in Mechanics, 2000,30(4):506-516.(In Chinese)

[2] CHEN G S, BRUNO R J, SALAMA M. Optimal placement of active/passive members in truss structures using simulated annealing[J]. AIAA Journal, 1991,29(8):1327-1334.

[3] LIU X, BEGG D W, MATRAVERS D R. Optimal topology∕actuator placement design of structures using SA[J]. Journal of Aerospace Engineering, 1997,10(3):119-125.

[4] ABDULLAH M M, RICHARDSON A, HANIF J. Placement of sensors/actuators on civil structures using genetic algorithms[J]. Earthquake Engineering & Structural Dynamics, 2001, 30(8):1167-1184.

[5] LIU D K, YANG Y L, LI Q S. Optimum positioning of actuators in tall buildings using genetic algorithm[J]. Computers & Structures, 2003, 81(32):2823-2827.

[6] 郭惠勇, 蒋健, 张陵. 改进遗传算法在MRFD半主动控制系统优化配置中的应用[J]. 工程力学, 2004, 21(2):145-151.

GUO Huiyong, JIANG Jian, ZHANG Ling. Optimal placement of MRFD using improved genetic algorithms[J]. Engineering Mechanics, 2004, 21(2):145-151.(In Chinese)

[7] LI Q S, LIU D K, TANG J,etal. Combinatorial optimal design of number and positions of actuators in actively controlled structures using genetic algorithm[J]. Journal of Sound & Vibration, 2004, 270(4/5):611-624.

[8] TAN P, DYKE S J, RICHARDSON A,etal. Integrated device placement and control design in civil structures using genetic algorithms[J]. Journal of Structural Engineering, 2005, 131(10):1489-1496.

[9] 吴亮红,王耀南,袁小芳,等.多目标优化问题的差分进化算法研究[J].湖南大学学报:自然科学版,2009,36(2):53-57.

WU Lianghong, WANG Yaonan, YUAN Xiaofang,etal. Research on differential evolution algorithm for mops[J]. Journal of Hunan University: Natural Sciences, 2009,36(2):53-57.(In Chinese)

[10]黄伟, 徐建, 朱大勇,等. 基于粒子群算法的隔振体系参数优化研究[J]. 湖南大学学报:自然科学版, 2014, 41(11):58-66.

HUANG Wei, XU Jian, ZHU Dayong，etal. Parameters optimization on particle swarm of vibration isolation system based optimization (PSO) algorithm[J]. Journal of Hunan University: Natural Sciences, 2014,41(11):58-66.(In Chinese)

[11]谭平, 宁响亮, 卜国雄,等. 结构主动控制的一体化多目标优化研究[J]. 振动工程学报, 2009, 22(6):638-644.

TAN Ping, NING Xiangliang, BU Guoxiong,etal. Integrated design and mult-objective optimization method for active control system[J]. Journal of Vibration Engineering, 2009,22(6):638-644.(In Chinese)

[12]MERZ P, FREISLEBEN B. Fitness landscapes, memetic algorithms, and greedy operators for graph bipartitioning[J]. Evolutionary Computation, 2000,8(1):61-91.

[13]KENNEDY J, EBERHART R. Particle swarm optimization[C]//Proceedings of IEEE International Conference on Neural Networks. New York: IEEE, 1995:1942-1948.

[14]STORN R, PRICE K. Differential evolution: a simple and efficient adaptive scheme for global optimization over continuous spaces[J]. Journal of Global Optimization, 1995,23(4):341-359.

[15]郑金华.多目标进化算法及其应用[M].北京:科学出版社, 2007:81-82.

ZHENG Jinhua. Multi objective evolutionary algorithm and its application [M]. Beijing: Science Press, 2007:81-82. (In Chinese)

[16]KIRKPATRICK S, GELATT C D, VECCHI M P. Optimization by simulated annealing[J]. Science, 1983,220(4598):671-680.

[17]李丽，牛奔.粒子群优化算法[M].北京:冶金工业出版社, 2009:34-36.

LI Li, NIU Ben. Particle swarm optimization algorithm [M]. Beijing: Metallurgical Industry Press, 2009:34-36.(In Chinese)

[18]OHTORI Y, CHRISTENSON R E, SPENCER JR B F,etal. Benchmark control problems for seismically excited nonlinear buildings[J]. Journal of Engineering Mechanics, 2004,130(4): 366-385.

[19]薛素铎,王雪生,曹资.基于新抗震规范的地震动随机模型参数研究[J].土木工程学报,2003,36(5):5-10.

XUE Suduo, WANG Xuesheng, CAO Zi. Parameters study on seismic random model based on the new seismic code[J]. China Civil Engineering Journal, 2003,36(5):5-10.(In Chinese)

Multi-objective Optimization of Structural Active Control System Using a New Hybrid Swarm Algorithm

PAN Zhaodong1, TAN Ping2†, ZHOU Fulin1,2

(1. College of Civil Engineering, Hunan University, Changsha 410082, China;2. Earthquake Engineering Research & Test Center, Guangzhou University,Guangzhou 510405, China)

This paper proposes a new multi-objective hybrid swarm optimization method for active control system based on particle swarm algorithm and differential evolution algorithm, in which the parameters of controller, and the number of and allocation of actuator are synchronously optimized. The basic idea is as follows: The different algorithms are used to complete the evolution of corresponding population, the non-dominated solution set is achieved based on the dealer principle, and the leader selection based on boundary point geometry center is adopted. Meanwhile, the simulated annealing algorithm is used for the secondary local search, the two indexes reflecting the structural vibration control effect and performance of control strategy are used as the optimization objective function. Finally, a ASCE 9-story benchmark model is used as a numerical example to validate the effectiveness of the proposed method. Compared with the conventional MODE, MOPSO, and MOHA algorithm, the MOHO-SA algorithm has better convergence curve and distribution of the pareto solution sets.

active control；hybrid swarm algorithm; two level search; multi-objective optimization; dealer principle; geometric center leader selection

1674-2974(2017)05-0020-07

10．16339/j．cnki．hdxbzkb．2017．05．003

2016-03-06 基金项目：国家自然科学基金资助项目(97315301-07，51408142), National Natural Science Foundation of China(97315301-07，51408142); 国家重点基础研究发展规划(973计划)项目(2012BAJ07B02)，Major State Basic Research Devolopment Program of China(973 Program)(2012BAJ07B02)；教育部创新团队项目(IRT13057),Program for Innovative Research Team in University(IRT13057) 作者简介：潘兆东(1986-)，男，陕西渭南人，湖南大学博士研究生 †通讯联系人，E-mail:ptan@gzhu.edu.cn

潘兆东1，谭平2†，周福霖1,2

(1.湖南大学 土木工程学院，湖南 长沙 410082；2. 广州大学 工程抗震研究中心，广东 广州 510405)

TU375.3

A