拱形棚洞受落石冲击的模型试验研究

王 爽, 周晓军, 罗福君, 姜 波, 朱 勇

(1. 西南交通大学 交通隧道工程教育部重点实验室, 成都 610031; 2.中铁二院, 成都 610031)

拱形棚洞受落石冲击的模型试验研究

王 爽1, 周晓军1, 罗福君1, 姜 波2, 朱 勇2

(1. 西南交通大学 交通隧道工程教育部重点实验室, 成都 610031; 2.中铁二院, 成都 610031)

通过室内模型试验对拱形棚洞抵抗落石冲击的力学性能进行了研究。重点分析了棚洞的拱圈、立柱和其内部钢筋在不同落石冲击能量、不同缓冲垫层厚度、不同冲击位置下的动力响应；分析了不同冲击工况下落石冲击力、拱形棚洞位移的变化规律；研究了拱形棚洞受落石冲击的破坏形态及其薄弱区域；并给出了相关加强措施和轻质土缓冲垫层的适宜厚度建议值。

拱形棚洞；模型试验；落石冲击；轻质土；动力响应

落石[1]是山区常见的地质灾害，其对公路、铁路等造成的危害是潜在的，后果是巨大的。由于落石灾害发生的随机性较大，目前对落石的研究方向主要集中在落石防护[2-4]。棚洞作为防护危岩落石灾害的重要结构被广泛应用到山岭隧道、高陡边坡工程中[5-7]。传统的框架形棚洞其结构形式简单，施工方便，其安全性已经得到工程实际的验证。但是框架形棚洞的自重大、跨度小等缺点仍然不能忽视。

拱形棚洞[8](见图1)，由于其结构形式的改善和轻质土垫层自重小的优点，其自重要小于框架形棚洞；此外，拱形棚洞可以不设置横梁，也不存在大跨度梁的问题，其适用性较广。因此，拱形棚洞能够克服框架形棚洞的显著缺点。但是，拱形棚洞在落石冲击作用下的安全性和力学性能目前尚不明确。

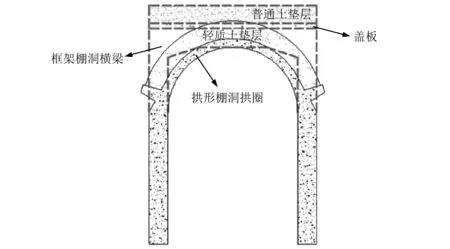
图1 框架和拱形棚洞的对比Fig.1 The comparison of frame and arch shed sheped tunnel

因此，本文通过模型试验以考察拱形棚洞的抵抗落石冲击的性能，进而为拱形棚洞的设计和工程应用提供依据。

1 模型试验简介

模型试验尺寸比例为1/10，模型尺寸，如图2所示。浇筑好的模型，如图3所示。本文通过改变落石的冲击能量考察拱形棚洞的动力响应规律。Muraishi等[9]的研究结果表明，1987—1997年，日本某铁路沿线落石冲击能量<1 000 kJ的事件达到了90%。基于此，本文根据相似定理，将落石冲击能量w限定在<1 000 J。并根据拱形棚洞的结构特点，考虑正向冲击和斜向冲击两种方式，如图2所示。

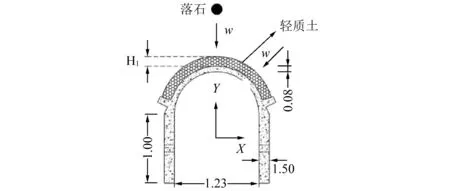
图2 拱形棚洞模型尺寸和正向斜向冲击示意图Fig.2 The dimension of arch shaped shed tunnel and schematic diagram of positive and oblique impacting

图3 拱形棚洞模型Fig.3 The model of arch sharped shed tunnel

为充分考察拱形棚洞在落石作用下的力学性能，模型试验中所开展的落石冲击实验工况包括：①落石正向冲击下，固定冲击能量为21.0 J，将轻质土垫层的厚度分别设置为10 cm、12 cm、14 cm、16 cm、18 cm；②落石斜向45°冲击下，固定冲击能量为21.0 J，将轻质土垫层的厚度分别设置为10 cm、12 cm、14 cm、16 cm、18 cm；③落石正向冲击下，固定轻质土垫层厚度为14 cm，将冲击能量定为21.0 J、37.8 J、54.8 J、71.0 J、92.4 J，5个等级；④将落石的冲击能量设定为169.1 J、213.4 J、454 J，进行破坏形态的试验。

棚洞上混凝土应变片的粘贴及其编号，如图4所示。

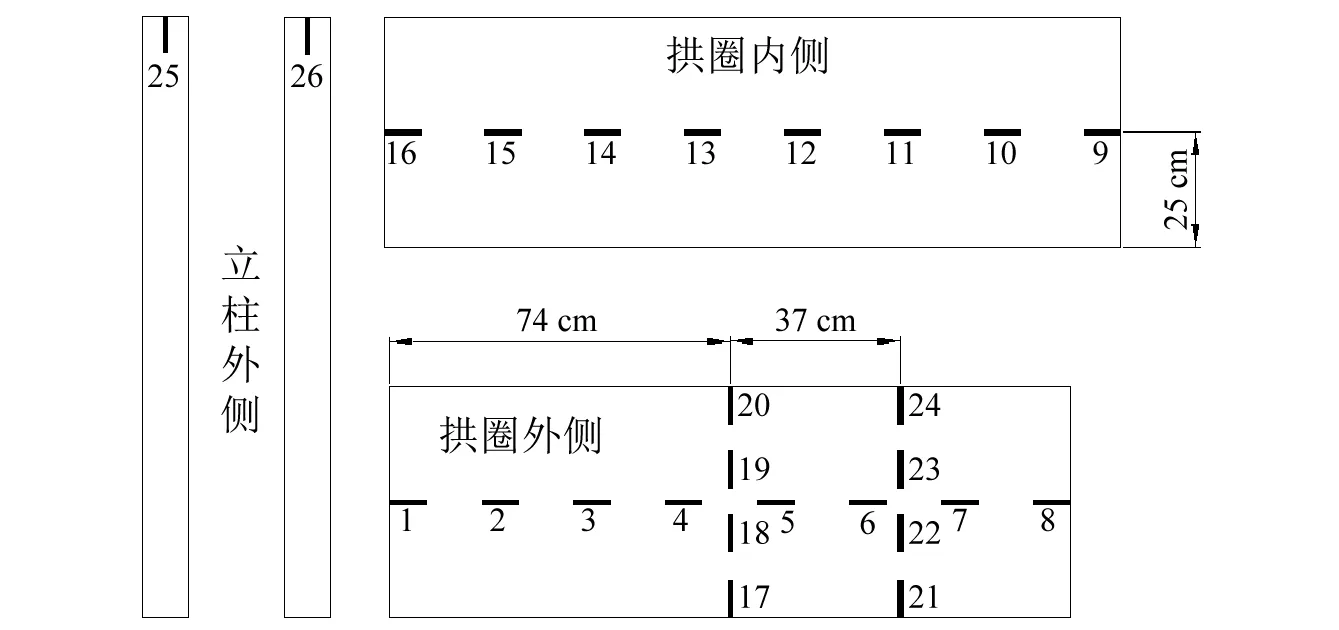
图4 应变片粘贴示意图Fig.4 The schematic diagram of gauge pasted

以下具体分析试验结果。

2 拱圈应变分析

2.1 拱圈环向应变分析

2.1.1 固定冲击能量

将落石的冲击能量固定在21.0 J，实际能量为210 kJ。将拱顶上部作为缓冲垫层的轻质土的厚度分别设为10 cm、12 cm、14 cm、16 cm、18 cm，监测到的拱圈典型应变时程曲线，如图5所示。

从图5可知，冲击瞬间应变时程曲线迅速波动，达到正负两个峰值，然后慢慢趋于稳定值，最后该应变时程曲线的稳定值和未冲击时的应变值相同，说明混凝土还处于弹性阶段，由此认为本试验中多次使用同一模型进行冲击试验是可信的。

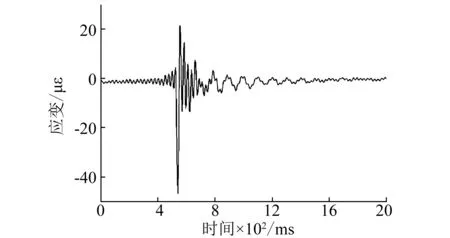
图5 典型的应变时程曲线Fig.5 The typical time-history curve of strain

将每个应变片在一次冲击过程中记录到的两个峰值中的绝对值较大者绘制，如图6所示。从图6可知，拱圈不同位置的应变情况。图6中正值表示受拉，负值表示受压。

从图6可知，5种厚度垫层下的拱圈应变变化图均相似，大致关于拱圈中线对称。拱圈顶部两侧应变为正值受拉，中间为负值受压。拱圈底部两侧应变为负值受压，中间两个应变片均为正值受拉。

从5个部位的应变片应变变化图可知，无论是拱圈顶部还是底部，左侧应变片监测到的应变值都较右侧大，这与试验过程中冲击位置并不在绝对中心有关。

从图6可知，拱圈5个部位的应变片应变值变化图还可以看出，随着缓冲垫层厚度的增加，各应变片的数值在减小；1号、2号应变片是受拉最突出的部位，图7列出了1号、2号应变片最大应变数值随垫层厚度的变化趋势图，可见其值是随着垫层厚度增加而减小的。

(a)10 cm厚垫层(b)12 cm厚垫层(c) 14 cm厚垫层

(d) 16 cm厚垫层 (e) 18 cm厚垫层图6 拱圈不同位置应变(με)Fig.6 The strain of arch(με)

图7 应变值随垫层厚度的变化Fig.7 The strain values under different cushion thickness

但总的来看，在该冲击能量作用、垫层厚度在10～18 cm之间变化的情况下，拱圈各部位的应变值都很小，最大值仅55 με，远远小于混凝土的极限拉应变2 000 με。

2.1.2 固定轻质土厚度

固定轻质土厚度为14 cm，将落石的冲击能量定为21.0 J、37.8 J、54.8 J、71.0 J、92.4 J的5个等级，考察在上述落石冲击能量作用下拱形棚洞的力学性能。

同样绘制拱圈的应变变化趋势，如图8所示。从图8可知，应变变化趋势与图6类似：两侧对称；左侧数值略大。

(a)21.0 J(b)37.8 J(c)54.8 J

(d)71.0 J (e)92.4 J图8 拱圈不同位置应变示意图(με)Fig.8 The strain of arch(με)

对比图8可知，随着落石冲击能量的增大，拱顶的应变变化曲线向下凹程度较为突出，拱圈底部的曲线也变得更加凸起。提取部分具有代表性的应变片，将其监测得到的应变值列于表1。

从表1可知，随着落石冲击能量的增加，总体上拱圈各部分应变的绝对值是逐渐增大的。但其最大值为85 με，仍远远小于混凝土的抗拉强度极限值2 000 με。

2.1.3 斜向冲击

同样将拱顶部位外层缓冲垫层的厚度值设为10 cm、12 cm、14 cm、16 cm、18 cm，落石的冲击能量固定为21.0 J，冲击位置则变为拱圈右侧45°处，在此工况下拱圈典型部位的应变变化趋势，如图9所示。

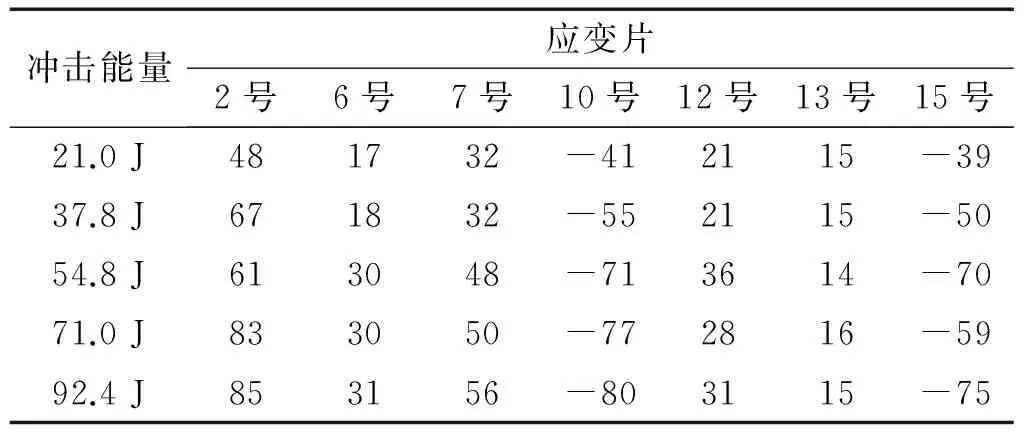
表1 部分应变片应变值随冲击能量的变化Tab.1 The strain values of part gauge change with impact energy με

从图9可知，在斜向冲击下，拱圈的应变变化趋势图的主要特点有：变化趋势曲线不对称；拱顶左侧和拱底右侧应变数值较大；随着垫层厚度的增加，各处的应变绝对值是整体上减小的。(试验数据由于采集原因发生错误。)

与正向冲击相比较，斜向冲击应变最大值发生在11号应变片处，在102～123 με之间变化，较正向冲击大；冲击点对侧的拱顶、拱底混凝土都受压，数值较正向冲击大。

总体而言，拱形棚洞遭受斜向冲击时较正向冲击不利，但其数值仍是同一数量级，二者最大的拉应变分别是123 με和55 με，都小于混凝土的极限拉应变2 000 με。

(a)10 cm厚垫层(b)12 cm厚垫层(c)14 cm厚垫层

(d)16 cm厚垫层 (e)18 cm厚垫层 (注：10 cm厚垫层下3号应变片数据由于采集原因发生较大误差，可信度较低。但为与其他工况下的试验数据相对应，图中仍保有监测到的数据)图9 拱圈不同位置应变示意图(με)Fig.9 The strain of arch(με)

2.2 拱圈纵向应变分析

在拱圈纵向正向冲击和斜向冲击点纵向分别布置了4个应变片，如图4所示。

在落石的正向冲击下，固定冲击能量，改变缓冲垫层的厚度，17号～20号应变片最大应变值见表2。从表2可知，17号和18号应变片应变值随垫层厚度变化不大，但19号应变片则变化幅值较大，在8～565 με，且规律不明显。经分析认为是每次冲击时，落石冲击点距离19号应变片最近，且每次冲击没有绝对完全冲击到同一点。但从19号应变片的应变值可以看出，最大值出现在垫层为10 cm的情况下，为565 με，其值仍小于混凝土的极限拉应变2 000 με。

对比拱圈环向应变值，显然纵向应变值较大，分析认为是拱圈纵向没有布置钢筋导致这一现象。

在正向冲击下，固定垫层厚度，变化冲击能量17号～20号应变片最大应变值，如表3所示。从表3中可知，18号、19号应变片的应变值都在安全范围内，且变化幅值不大。但17号应变片在54.8 J冲击下的数值为1 857。分析认为，造成17号、20号应变片的应变值较大，且出现塑性区的原因还是拱圈没有布置纵向钢筋。

表2 17号～20号应变片应变值Tab.2 The strain values of No.17～20 με

在斜向冲击下，固定冲击能量为21 J，改变垫层厚度，21号～24号应变片的应变值，见表4。从表4可知，21号、22号、24号应变片应变值变化不大，仅23号应变片变化幅度较大，且数值都较其他应变片大，经分析认为是落石冲击位置跟23号应变片最近。从23号应变片的应变值可知，最大值出现在垫层为10 cm的情况下，为651 με，小于混凝土的极限拉应变2 000 με。

表3 17号～20号应变片应变值Tab.3 The strain values of No.17～20 με

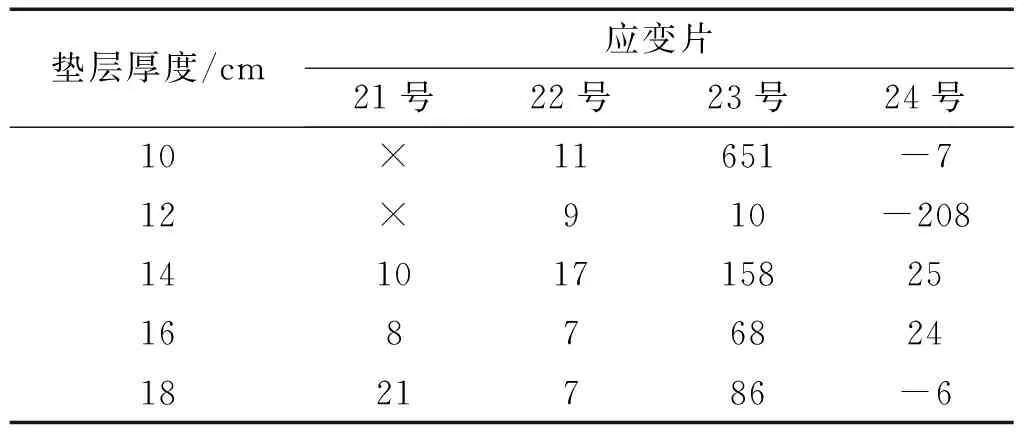
表4 21号～24号应变片应变值Tab.4 The strain values of No.21～24 με

总的来看，拱圈纵向应变明显较环向应变大；且最大值发生在纵向最边缘处。经分析认为，这两个特点都与拱圈没有配置纵向钢筋有关。

3 立柱和钢筋应变分析

3.1 立柱应变分析

两侧立柱外侧顶部分别粘贴有1个应变片，监测立柱应变情况，两个应变片编号是25号、26号。

在正向冲击下，固定冲击能量为21.0 J，改变垫层厚度，25号、26号应变片最大应变值见表5。从表5可知，随着垫层厚度的变化，应变片最大值全是正值受拉；数值随垫层厚度变化不大；确定的垫层厚度下，25号、26号应变片的应变值几乎相同，分析认为这是由于结构、受力对称；应变最大值仅为30 με。

表5 25号、26号应变片应变值Tab.5 The strain values of No.25～26 με

正向冲击下，固定垫层厚度，改变冲击能量，25号、26号应变片最大应变值，见表6。从表6可知，随着冲击能量的增大，两处混凝土总体上的应变值是增大的；同一冲击能量下，两处应变片的应变值相差很小；最大应变值为53 με。

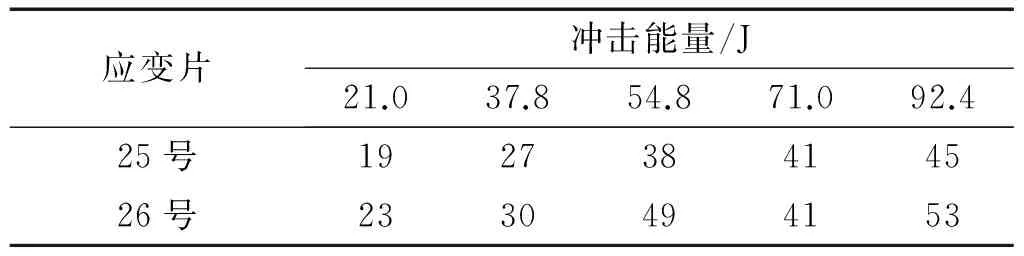
表6 25号、26号应变片应变值Tab.6 The strain values of No.25～26 με

斜向冲击下，固定冲击能量为21 J，改变垫层厚度，25号、26号应变片的应变值，见表7。从表7可知，随着垫层厚度的变化，两处混凝土的应变值变化很小；25号应变片应变值全为负值，26号应变片全为正值，经分析是因为25号应变片粘贴在冲击侧的立柱上受压，26号应变片则是对侧受拉；最大应变值为9 με。

表7 25号、26号应变片应变值Tab.7 The strain values of No.25～26 με

总体上看，固定冲击能量情况下，厚度对立柱影响较小；不同冲击能量情况下，立柱应变不断增加；斜向冲击下，一侧立柱受压，一侧受拉。

总的来说，与拱圈相比较，落石冲击对立柱影响较小；斜向冲击对立柱影响小于正向冲击。

3.2 钢筋应变分析

立柱和拱圈内钢筋也分别粘贴有应变片，监测钢筋的轴向应变。其中立柱顶部内侧是27号应变片，拱圈中部是28号应变片，拱圈斜向冲击点处是29号应变片。但由于28号应变片在模型浇筑过程中损坏，以下仅有27号、29号的数据。

正向冲击下，固定冲击能量为21 J，变化垫层厚度，27号、29号应变片最大应变值，见表8。从表8可知，随着垫层厚度的变化，两处钢筋的应变值变化较小；27号应变片受拉，29号应变片受压；最大值为20 με。

表8 27号、29号应变片应变值Tab.8 The strain values of No.27～29 με

在正向冲击下，固定垫层厚度，变化冲击能量，27号、29号应变片最大应变值，见表9。从表9可知，随着冲击能量的增大，两处混凝土总体上的应变值是增大的；27号应变片受拉，29号应变片受压；最大应变值为38 με。

表9 27号、29号应变片应变值Tab.9 The strain values of No.27～29 με

在斜向冲击下，固定冲击能量为21.0 J，改变垫层厚度，27号、29号应变片的应变值，见表10。从表10可知，随着垫层厚度的变化，27号应变片应变值变化不大，29号应变值有减小的趋势；27号应变片受压，29号应变片受拉，这点与前两组工况相反，经与“2.1”中的拱圈应变变化趋势图对比分析，认为原因是冲击点的变化导致11号应变片附近的混凝土受拉，导致靠近钢筋的29号应变片也受拉。同理，斜向冲击时，拱圈顶部混凝土受压，内部钢筋即27号应变片也受压；最大应变值为48 με。

表10 27号、29号应变片应变值Tab.10 The strain values of No.27～29 με

总体上看，在固定冲击能量的情况下，厚度对钢筋应变影响较小；不同冲击能量情况下，钢筋应变不断增加；斜向冲击下，冲击点位置对应的钢筋受拉，立柱顶部钢筋受压；但各项工况钢筋应变数值都很小。

总的来说，与拱圈相比较，落石冲击对钢筋影响较小；斜向冲击对钢筋影响大于正向冲击。

4 位移分析

在正向冲击下，固定冲击能量为21 J，变化垫层厚度，拱圈底部的竖向位移，见表11。从表11可知，随着垫层厚度的增大，拱顶位移总体上呈现减小的趋势；位移最大值为0.31 mm。

表11 拱顶竖向位移值Tab.11 The vertical displacement of vault

在斜向冲击下，固定冲击能量为21 J，变化垫层厚度，立柱顶部的水平向位移，见表12。从表12可知，随着垫层厚度的增大，拱顶位移总体上呈现减小的趋势；位移最大值为1.53 mm。

表12 立柱水平位移值Tab.12 The horizontal displacement of upright column

在正向冲击下，拱顶位移随着垫层厚度的增大而减小；斜向冲击下，立柱顶部水平位移随着垫层厚度的增加而减小；斜向冲击下，立柱的水平位移大于拱圈在正向冲击下的竖向位移。

拱圈和立柱的两处位移值的变化充分反映了不同厚度垫层的缓冲效果；拱形棚洞结构承受水平荷载的能力较弱，导致斜向冲击下，立柱的水平位移较大。

5 冲击力分析

通过记录到的加速度时程曲线，如图10所示。获取不同冲击工况下的最大加速度值，按照F=ma得到最大冲击力。具体分析如下：

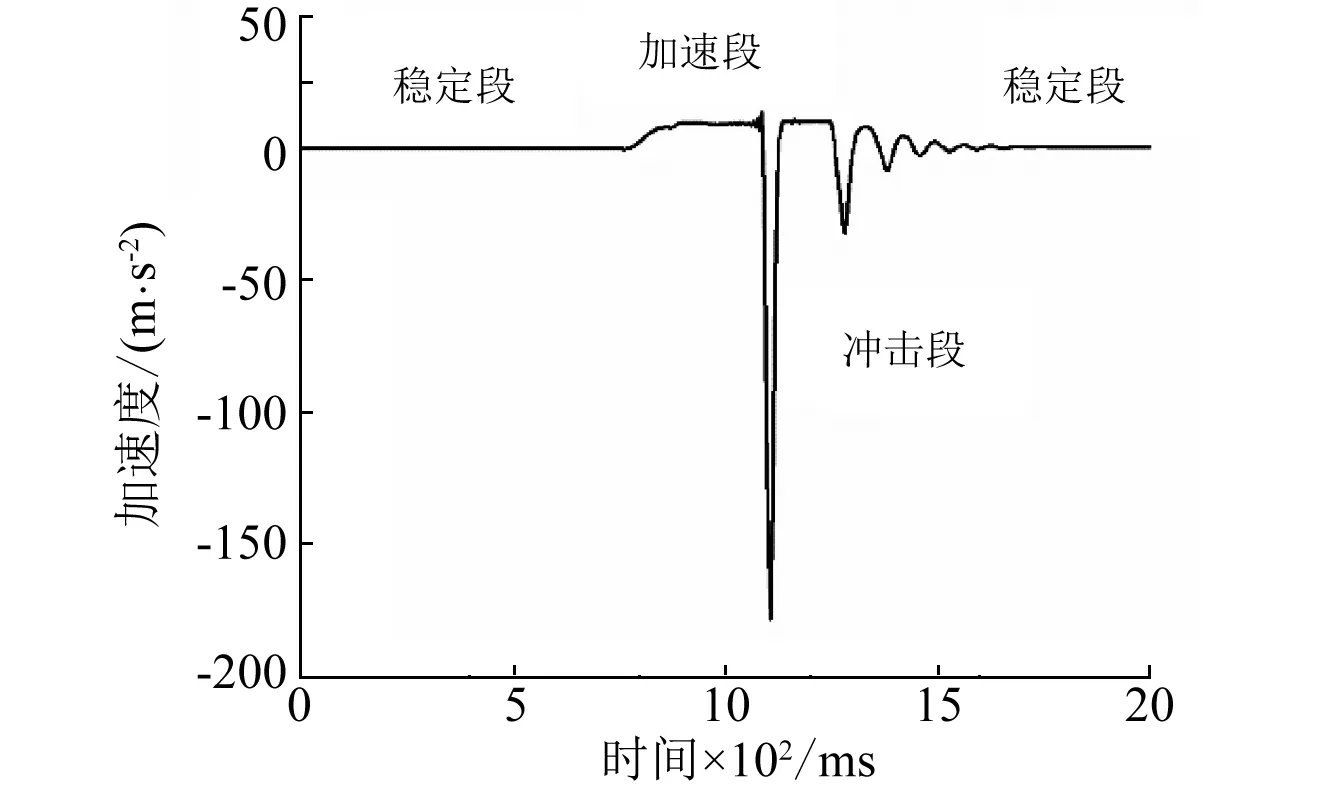
图10 典型的加速度曲线Fig.10 Typical time-history curve of acceleration

在正向冲击下，固定冲击能量为21.0 J，变化垫层厚度，冲击力，见表13。从表13可知，冲击力随着垫层厚度的变化很小；冲击力在1 248～1 766 N之间分布。

表13 不同厚度垫层下的冲击力Tab.13 The impact force under different thickness cushion

在正向冲击下，固定垫层厚度，变化冲击能量，冲击力，见表14。从表14可知，冲击力随着冲击能量的增大而增大；最大冲击力为2 316 N。

表14 不同冲击能量冲击下的冲击力Tab.14 The impact force under different impact energy

在斜向冲击下，固定冲击能量为21 J，改变垫层厚度，冲击力，见表15。从表15可知，冲击力随着垫层厚度的变化很小；冲击力分布在682～950 N。

表15 不同厚度垫层下的冲击力Tab.15 The impact force under different thickness cushion

相同冲击能量冲击下，冲击力变化很小；冲击力随着冲击能量的增大而增大；相同冲击能量冲击下，斜向冲击监测到的冲击力较正向冲击力小，经分析认为是由于落石并没有完全与垫层平面垂直相撞，如图11所示。导致加速度计监测到的最大加速度值较小。

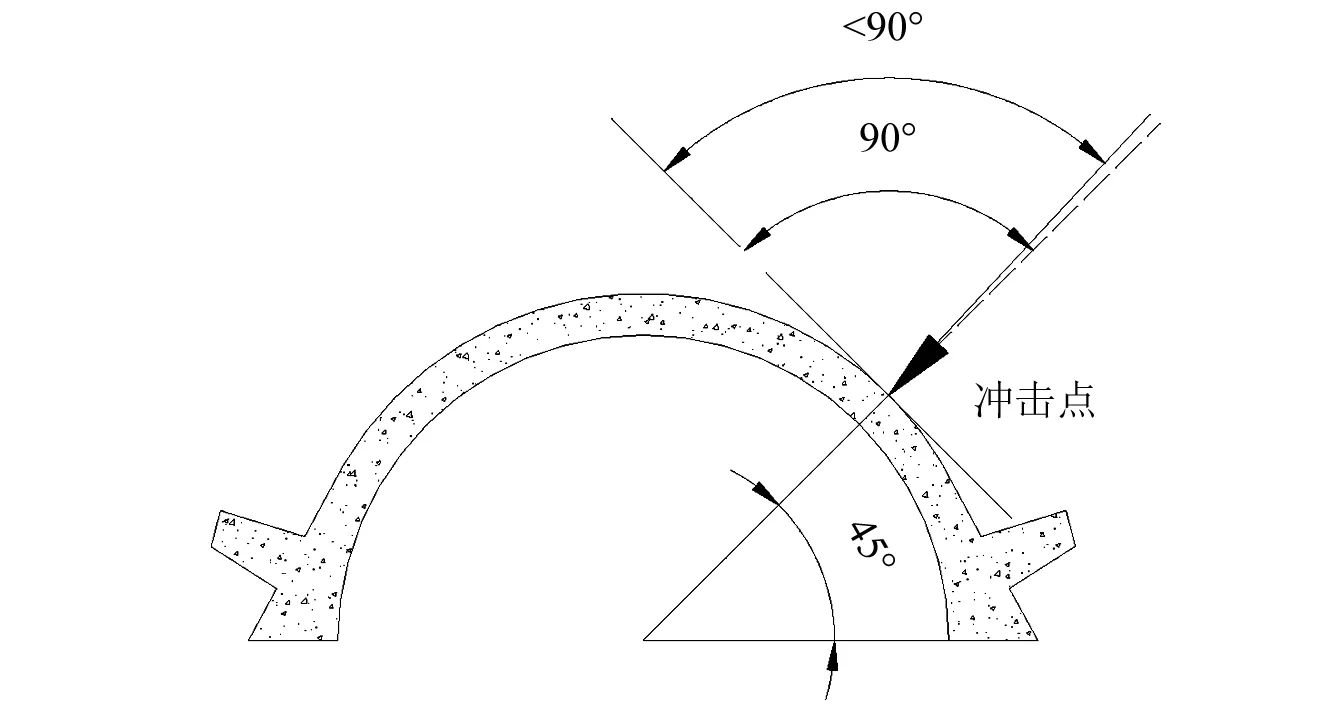
图11 斜向冲击位置不垂直示意图Fig.11 The schematic diagram of non-vertical of oblique impacting

6 破坏形态分析

在完成以上所有工况的冲击试验之后，将落石分别从2.56 m和3.26 m的高度放下，分别对应169.1 J和213.4 J的冲击能量，并撤除所有垫层，让落石直接砸向棚洞，考察拱形棚洞的破坏形态。

在该两级冲击能量的冲击下，拱形棚洞的拱圈出现了一些裂缝，之前承受斜向冲击一侧的挡墙已脱落，如图12所示。

图12 拱圈裂缝与损坏Fig.12 The crack and damage of arch ring

在前两次冲击能量冲击后，棚洞仍然保持整体性，具有抵抗落石冲击的能力，所以利用现场的混凝土试块继续冲击棚洞，冲击能量约为454 J。

冲击后棚洞的破坏形态，如图13所示。在该冲击能量下，拱圈发生了局部破坏；之前承受斜向冲击侧，拱圈外侧产生了纵向贯穿裂缝，对称侧则没有；另一侧未掉落的挡墙与立柱和拱圈连接处产生了裂缝。

图13 拱形棚洞破坏形态Fig.13 The damage mode of arch shaped shed tunnel

总结与分析：随着冲击能量的增大，棚洞产生的破坏越来越严重；由于没有钢筋，两侧挡墙承载能力较弱，容易脱落；拱圈约45°裂纹集中，受力较大；除拱圈和挡墙外，拱形棚洞其余部分未见明显裂缝和损伤区域。综合分析得到拱圈较为薄弱的区域，如图14所示。

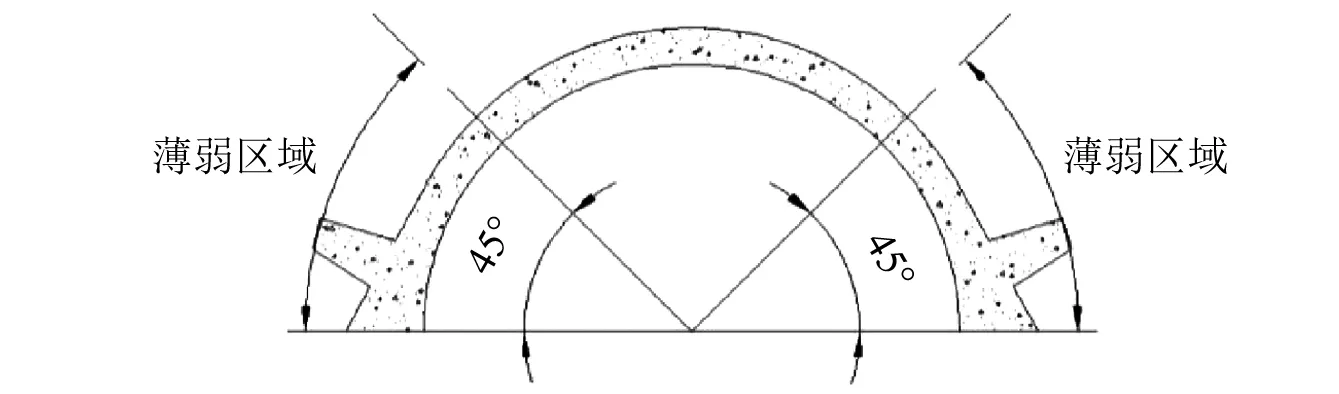
图14 拱圈薄弱区域Fig.14 The weak area of arch ring

7 结 论

通过对拱形棚洞在落石冲击作用下的力学性能的模型试验研究，主要得到以下结论：

(1)拱形棚洞承受落石冲击荷载的主要部分是拱圈；根据其在落石冲击作用下的破坏形态试验结果，拱圈较为薄弱的区域是45°内包含的区域，如图14所示；

(2)在不同能量的落石冲击下，拱顶外侧缓冲垫层厚度对拱圈和钢筋的受力有明显影响，但对立柱影响较小；

(3)在21.0～92.4 J冲击能量范围内，无论是正向冲击还是斜向冲击，棚洞各部分的混凝土应变值都远小于其极限应变值；

(4)在21.0～92.4 J冲击能量范围内，拱圈顶部混凝土纵向应变出现了相对于环向应变的较大值(<1 000 με)，分析认为是拱圈内没有纵向钢筋所致。

(5)对于实际工程中的拱形棚洞，其顶部外侧设置轻质土缓冲层时能够承受210～924 kJ能量落石的冲击荷载，且不产生损坏；

(6)本文拱形棚洞在承受92.4 J(即实际情况中924 kJ)的冲击能量时而不产生损伤，根据Muraishi的研究成果，可以得出此种棚洞结构能够承受绝大多数落石的冲击，可以使用于实际工程中。

通过对室内试验测试结果的分析，若将拱形棚洞应用于实际工程中，提出如下建议：①拱形棚洞的拱圈两侧的挡墙内应配置一定数量的受力钢筋；②拱圈应配有纵向受拉钢筋，两侧挡墙也应配制一定数量的受力钢筋。

[1] 何思明,沈均,罗渝，等.滚石坡面法向冲击动力响应特性研究[J].工程力学,2011,28(6):118-124.

HE Siming, SHEN Jun, LUO Yu, et al. Study on the characteristics of normal impact of post-earthquake rock-fall on slope [J]. Engineering Mechanics, 2011,28(6): 118-124.

[2] PIERSON L. Rockfall catchment area design guide[R]. Salem: Oregon Department of Transportation-research Group,2001.

[3] 陈江, 夏雄. 金温铁路危石治理中柔性防护技术应用研究[J]. 岩石力学与工程学报, 2006, 25(2): 312-317.

CHEN Jiang，XIA Xiong． Research on application of flexible protection technique Jinhua-Wenzhou railway rockfall treatment[J]．Chinese Journal of Rock Mechanics and Engineering，2006，25( 2) : 312-317.

[4] 孙波, 石少卿, 汪敏. 落石冲击被动防护系统能量衰减规律分析[J]. 中国地质灾害与防治学报, 2010, 21(4): 34-38.

SUN Bo,SHI Shaoqing,WANG Min. Analysis of the rhythm of energy attenuation when rockfalls impact on the passive protection[J].The Chinese Journal of Geological Hazard and Control,2010,21(4):34-38.

[5] 冉利刚,陈赤坤. 高速铁路棚洞设计[J]. 铁道工程学报,2008,25(6):61-66.

RAN Ligang,CHEN Chikun. The design of the hangar tunnel of high-speed railway[J]. Journal of Railway Engineering Society, 2008,25(6):61-66.

[6] 刘天翔,何思明,王东坡,等. S210线轻钢结构滚石防护棚洞动力响应与优化研究[J]. 灾害学,2015,30(1):69-74.

LIU Tianxiang， HE Siming， WANG Dongpo， et al. Dynamic response and optimization study about light steel rock-shed on the S210 road[J].Journal of Catastrophology,2015,30( 1) : 69-74.

[7] 李现宾. 成昆线危岩落石病害整治中的棚洞设计[J]. 现代隧道技术,2009(5):19-22.

LI Xianbin. Shelter-tunnel design for dealing with stone-falling disasters on Chengdu-Kunming railway[J]. Modern Tunnelling Technology,2009(5):19-22.

[8] 周晓军.用于桥隧连接的连接结构: ZL201420221974.8[P]. 2014-10-08.

[9] MURAISHI H, SAMIZO M, SUGIYAMA T. Development of a flexible low-energy rockfall protection fence[J]. Quarterly Report of RTRI, 2005. 46(3):161-166.

An experimental study on the performance of an arch shaped shed tunnel due to the impact of rockfall

WANG Shuang1, ZHOU Xiaojun1, LUO Fujun1, JIANG Bo2, ZHU Yong2

(1. Key Laboratory of Transportation Tunnel Engineering, Ministry of Education, Southwest Jiaotong University, Chengdu 610031, China;2. China Railway Eryuan Engineering Group Co.,Ltd., Chengdu 610031, China)

Model test was used to study the impact resistance of an arch shaped shed tunnel, which mainly analyzed the dynamic response rules of the arch, the upright column and the interior steel under diverse impact energy, cushion with diverse thickness, diverse impact locations. The rules of rockfall impact force and displacement of the arch shaped shed tunnel under diverse impacting condition were analyzed; Failure modes and weak area of the arch shaped shed tunnel were analyzed. The relative strengthening measures and appropriate thickness range of light soil cushion were given.

arch shed shaped tunnel; model test; rockfall impact; light soil; dynamic response

铁道部科技研究开发计划项目(2010G018-C-1-3)

2015-06-29 修改稿收到日期： 2016-04-29

王爽 男，硕士，1990年生

周晓军 男，教授， 1969年生

Email：zhouxjyu69@163.com

U25

A

10.13465/j.cnki.jvs.2017.12.035