基于马田系统的滚动轴承初始故障检测和状态监测

剡昌锋, 朱 涛, 吴黎晓, 贝 克, 郭剑锋

(1.兰州理工大学 机电工程学院，兰州 730050； 2.中核兰铀公司，兰州 730060)

基于马田系统的滚动轴承初始故障检测和状态监测

剡昌锋1, 朱 涛1, 吴黎晓1, 贝 克1, 郭剑锋2

(1.兰州理工大学 机电工程学院，兰州 730050； 2.中核兰铀公司，兰州 730060)

针对轴承寿命的四个阶段中振动信号特征参数的变化灵敏度不同，分析了特征参数对初始故障的敏感性和退化状态的相关性，提出了一种采用马田系统检测轴承初始故障和区分性能退化状态的方法。以对初始故障敏感和对退化状态相关的特征参数建立了马田系统的基准空间，并在马田系统中将两组特征参数融合为单一的特征参数马氏距离； MD1对滚动轴承初始故障的敏感性，检测轴承寿命在第一和第二阶段时出现初始故障的时间点； MD2随着滚动轴承性能退化状态而不断增大，依据其变化趋势判断轴承的退化状态；该方法避免了单一特征参数在不同运行环境中的不确定性和不稳定性，可以准确的检测出轴承的初始故障和判断轴承的退化状态。通过两组滚动轴承加速寿命试验，验证了该方法的有效性和准确性。

马田系统；滚动轴承；初始故障；状态监测；相关性；

旋转机械被广泛应用于电力、石油、化工、冶金、机械、航空航天等重要工程领域，滚动轴承作为旋转机械的关键部件，其性能退化或者失效将影响整机性能甚至导致设备非计划停机，造成经济损失甚至人员伤亡。据统计，约30%的旋转机械故障是由于滚动轴承的损伤所造成的[1]。由于滚动轴承寿命分散性比较大，传统的定时维修往往造成“维修不足”或者“维修过剩”，因此，滚动轴承初始故障的检测和性能退化状态的监测，对于保障设备长期安全、稳定运行和预知维修具有重要意义[2]。

近年来，许多学者在滚动轴承故障诊断方面做了大量的研究工作[3]，但是对轴承初始故障的识别和状态监测分析方面还需要进一步的研究。轴承从出现故障到失效还有一段时间，如果采用初始故障检测和状态监测，尽早发现轴承故障，在失效前合理安排维修时间，就可以避免非计划停机，减少维修成本，提高产品生产率。滚动轴承从出现故障到失效，建立一个合适的评价指标非常重要。由于单一的特征参数受抗干扰性差、敏感度低和包含信息少等缺点的制约，不能全面有效的评估轴承的性能退化状态，因此，多参数评估滚动轴承的性能退化状态得到了广泛的应用。Zhao等[4]采用主成分分析进行多参数融合，应用互信息监测轴承的健康状况。Shakya等[5]一方面应用马田系统对轴承的健康状况进行在线监测，通过切比雪夫不等式判断轴承的状态变化；另一方面应用正交化的马田系统(Mahalanobis Taguchi Systen, MTS)识别滚动轴承故障类型并提出了缺陷发生指数[6]。Yu[7]通过动态主成分分析提取特征参数，采用基于马氏距离(Mahalanobis Distance, MD)的隐马尔卡夫模型对轴承的性能退化状态进行在线监测。Wang等[8]应用基于EMD-SVD的马田系统，对轴承故障和退化状态进行监测。余发军等[9]应用改进型的K-SVD字典学习算法和峭度最大化原则的稀疏分解算法提取滚动轴承早期故障特征参数。Lim等[10]分别应用滚动轴承振动信号低频和高频特征参数对轴承状态的第二、第三阶段进行跟踪监测。Hu等[11]应用MTS-SOM系统对轴承初始故障和退化状态进行跟踪监测。Soylemezoglu等[12]应用马田系统对滚动轴承进行故障检测和寿命预测。Shen等[13]应用基于支持向量机的方法提取特征参数，该特征的发展趋势与轴承的故障发展趋势和运行时间相符合。Zhu等[14]采用基于SVDD的IRSVDD方法构建轴承的性能退化指标，克服了SVDD的缺点。Yan等[15]采用EMD和峭度相结合的方法，对轴承初始故障的时间进行估计。Kang等[16]通过二进制算法对轴承早期故障进行诊断和分类。Bhende等[17]采用声发射技术对滚动轴承早期故障进行检测和分类。目前多参数评估轴承退化状态主要集中于多参数融合技术、各阶段监测技术以及模型预测技术等方面。但是，多参数评估轴承退化状态中存在两个重要的问题：首先是要选择合适的特征参数，该参数对轴承的退化状态比较敏感并且其变化规律符合轴承的性能退化状态；其次，需要选择合适的方法，使得新的特征参数能够正确反映轴承的性能退化状态。

针对以上问题，本文提出了应用敏感性和相关性分析分别优化滚动轴承初始故障检测和状态监测时马田系统的基准空间，选择对初始故障敏感和退化状态相关的特征参数构建马田系统的基准空间，根据优化后马氏距离的变化趋势，判断轴承的初始故障和退化状态。马氏距离MD1在轴承出现故障时其幅值快速增大，随着故障的发展又回落到正常水平，根据其变化规律，检测轴承的初始故障。马氏距离MD2随着故障的发展而不断增大，当轴承状态发生改变时，其变化更加明显，根据其变化规律，判断轴承的退化状态。该方法确定的特征参数降低了马田系统原始基准空间的维度，其特征参数的变化趋势更加符合轴承初始故障和性能退化状态的特点，根据马氏距离的变化趋势可以准确的判断轴承的初始故障和退化状态。

1 马田系统基本原理

马氏距离MD是由印度统计学家Mahalanobis P C于1936年提出的，表示数据的协方差距离[18]。与欧式距离相比，马氏距离不受量纲的影响，两点之间的马氏距离与原始数据的测量单位无关；由标准化数据和中心化数据(即原始数据与均值之差)计算出两点之间的马氏距离。

马田系统MTS是田口玄一博士提出的一种研究多维系统的方法，该方法将马氏距离与田口方法进行了有效集成，被广泛应用于疾病诊断、数据分类、模式识别以及样本的诊断、预测分析[19]。

本文通过分析滚动轴承振动信号特征参数对初始故障的敏感性和退化状态的相关性优化马田系统的基准空间，根据优化后马氏距离的变化趋势检测轴承的初始故障和退化状况，主要包括以下步骤[20]：①基准空间的确定；②基准空间的有效性验证；③基准空间的优化；④计算样本空间的马氏距离。

1.1 基准空间的确定

为了区分滚动轴承存在故障时马氏距离的变化特征，在构建马田系统基准空间时采用滚动轴承无故障时样本的特征参数作为马田系统的基准空间，根据马氏距离的变化趋势，判断轴承的性能退化状态。

步骤1 构建基准空间特征参数

假定有m个特征参数，n个样本，则第i次采集数据的第j个特征参数可以表示为Xij，第i个样本的特征参数可以表示为Xi=(Xi1,Xi2, …,Xij,Xim)，则n个正常样本特征参数的基准空间可以表示为：

(1)

步骤2 基准空间标准化

(2)

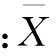
步骤3 计算标准化后基准空间的马氏距离

(3)

1.2 基准空间的有效性验证

为了验证基准空间的有效性，采集滚动轴承无故障阶段和故障阶段时的振动信号样本，利用基准空间的均值、方差、相关矩阵对两组样本的基准空间进行标准化并计算其马氏距离。如果故障样本的马氏距离明显大于正常样本的马氏距离，则证明所建立的基准空间是有效的；否则，需要重新选择特征参数定义基准空间。

1.3 基准空间优化

滚动轴承初始故障检测和状态监测过程中并非所有的特征参数都有助于提高计算精度，有些特征参数甚至存在干扰，因此，为了简化马氏距离的计算、缩短计算时间、提高诊断精度，需要对原始马田系统的基准空间进行特征优化，选择有效的特征参数构建马田系统的基准空间。在滚动轴承初始故障检测过程中，选择对初始故障比较敏感的特征参数构建马田系统基准空间；状态监测过程中选择与轴承退化状态相关的特征参数构建马田系统的基准空间。优化后的特征参数其变化趋势更加符合轴承初始故障和退化状态的特点，基准空间特征参数数目更少，计算更加简单、高效，结果更加可靠。

1.4 样本空间的马氏距离

(4)

(5)

2 滚动轴承初始故障和状态监测特征参数选择

2.1 特征参数

滚动轴承初始故障检测和状态监测能否成功，在很大程度上取决于特征参数的选择。滚动轴承振动信号分析中，常用的特征参数有时域特征、频域特征和时频特征。本文所选用的特征有时域特征：平均值、均方根、峰值、偏度、峭度、波峰因子、裕度因子、形状系数、脉冲系数；频域特征有：轴承内圈、外圈、滚动体、保持架的特征频率幅值。各个特征计算方法如下[21]：

(6)

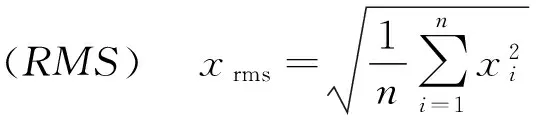
(7)

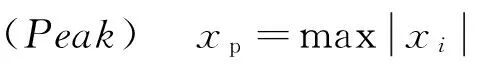
(8)

(9)

5)峭度(Kurtosis)

(10)

(11)

7)裕度因子(Clearance factor)

(12)

(13)

(14)

10)外圈特征频率幅值：xbpfo

11)内圈特征频率幅值：xbpfi

12)滚动体特征频率幅值：xbsf

13)保持架特征频率幅值：xftf

式中：xm为样本数据的均值，xstd为样本数据的标准差。xm计算公式如下：

(15)

滚动轴承特征频率根据轴承几何参数中的滚子数目z、滚动体直径d、节圆直径D、接触角α以及轴承转速n可以计算得到轴承的特征频率[22]。滚动轴承特征频率的幅值根据样本时域信号的快速傅里叶变换计算得到。

2.2 滚动轴承初始故障特征参数选择

2.2.1 初始故障特征参数敏感性分析

滚动轴承特征参数在初始故障时的敏感性主要指在初始故障期间特征参数达到峰值时的时间和幅值，也就是其特征参数达到峰值时的上升率，时间越短、幅值越大，其敏感性越高。为了准确描述各个特征参数在初始故障时的敏感性，采用滚动轴承第二阶段时特征参数的峰值yp和时间xp的比值作为衡量敏感性s大小的标准。为了比较每个样本特征参数敏感性的大小，消除幅值y在不同特征之间幅值差异的影响，计算敏感性s在不改变特征参数变化趋势的情况下，对每个特征参数进行归一化处理。

步骤1 特征参数归一化

假定有n个样本，则该样本的某一个特征参数可以表示为X=(x1,x2, …,xi, …,xn)，其归一化如下：

(16)

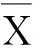
步骤2 敏感性计算

(17)

根据式(16)和式(17)可以对滚动轴承每一个特征参数进行归一化和敏感性计算。特征参数的归一化处理，避免了计算敏感性时不同特征参数幅值差异的影响，使每个特征参数的敏感性具有可比性。

2.2.2 初始故障特征参数选择

滚动轴承的初始故障能否准确检测，与初始故障特征参数选择有很大的关系。滚动轴承初始故障检测中选择对初始故障敏感性较高的特征参数作为马田系统的基准空间，根据马氏距离的变化趋势检测轴承的初始故障。

为了分析滚动轴承初始故障时的敏感性，本论文所用实验数据来源于IEEE PHM 2012，试验采用的PRONOSTIA

平台，如图1所示[23]。数据采集中，采样频率为25.6 kHz，每次采集数据的时间间隔为10 s，采样时间为0.1 s，每个样本包含2 560个数据点。实验的第1组数据共有1 416个样本，其样本的13个特征参数变化趋势，如图2～图14所示。该实验采集了滚动轴承加速寿命实验中轴承从完好到自然失效时全寿命周期的数据。

图1 PRONOSTIA试验平台Fig.1 Test rig of PRONOSTIA

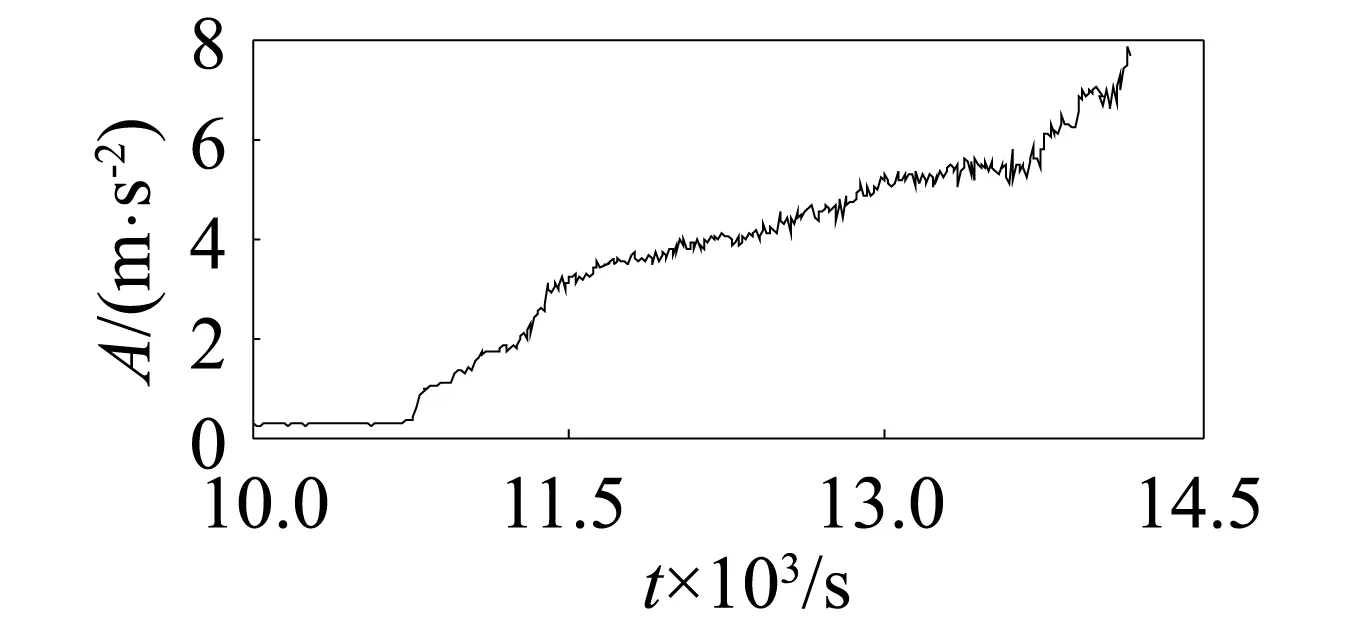
图2 平均值Fig.2 Average

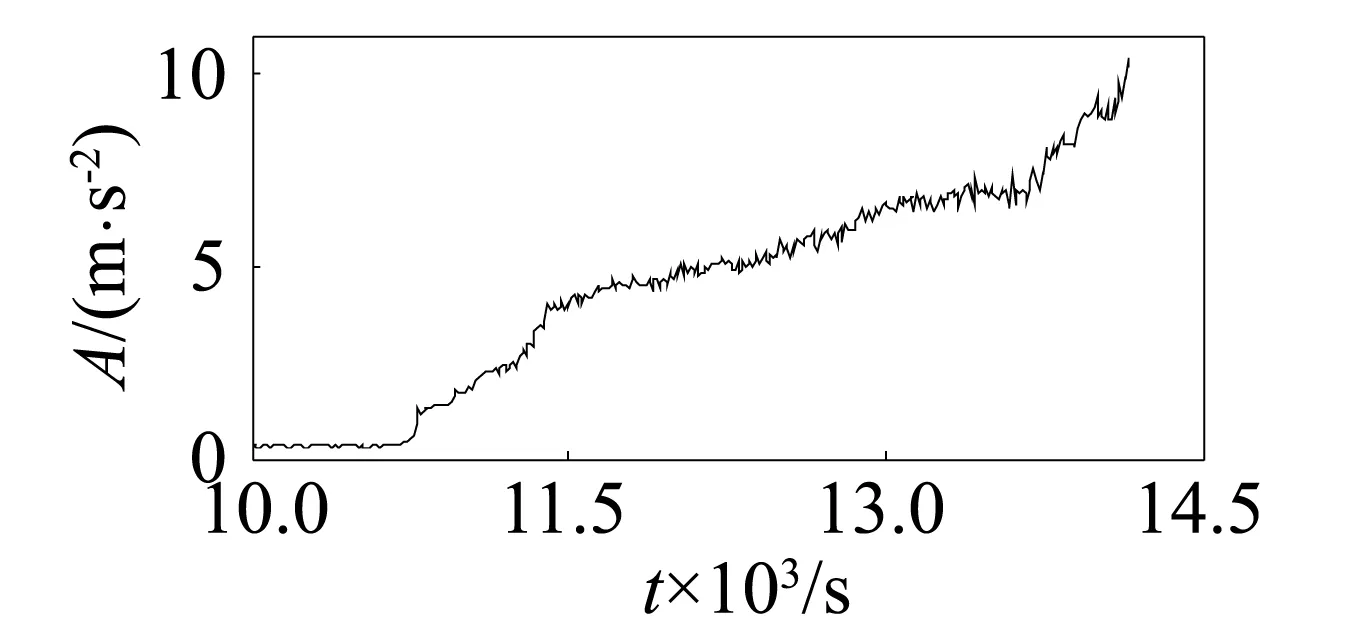
图3 均方根Fig.3 RMS

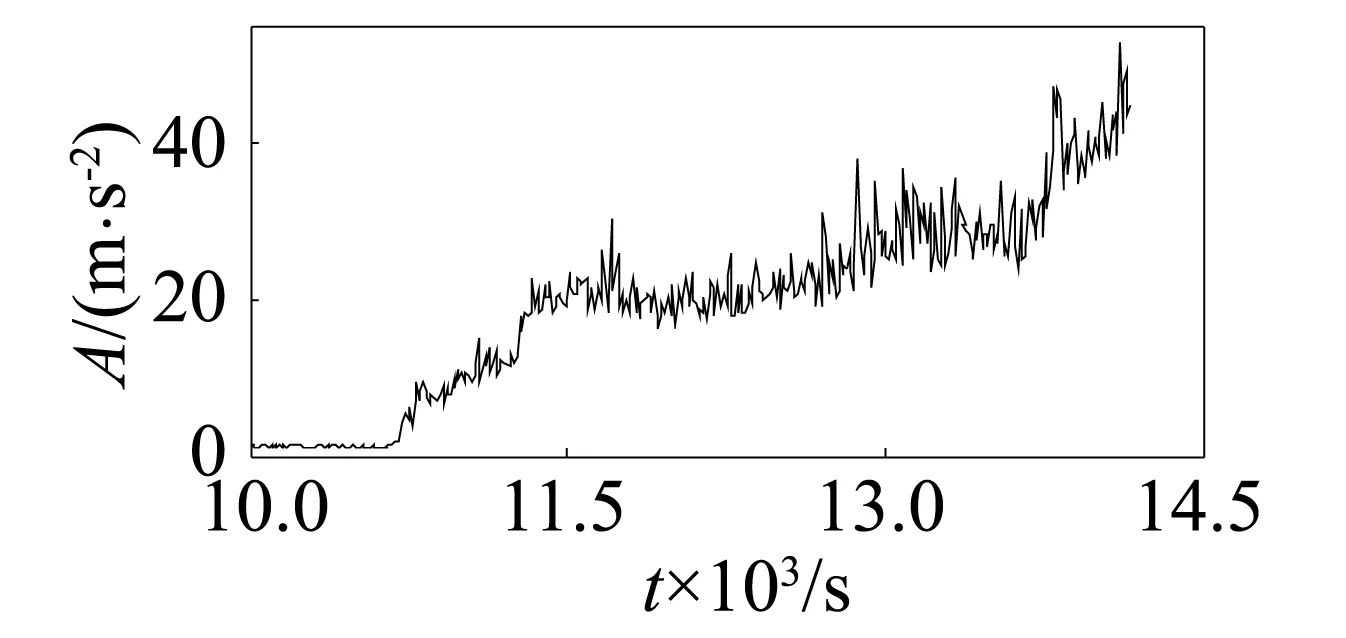
图4 峰值Fig.4 Peak

图5 偏度Fig.5 Skewness

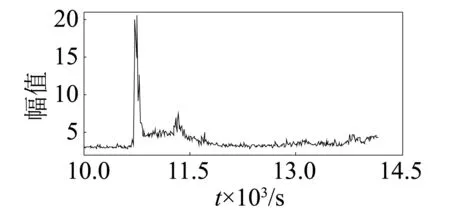
图6 峭度Fig.6 Kurtosis

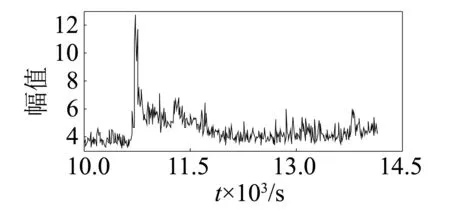
图7 波峰因子Fig.7 Crest factor

图8 裕度因子Fig.8 Clearance factor

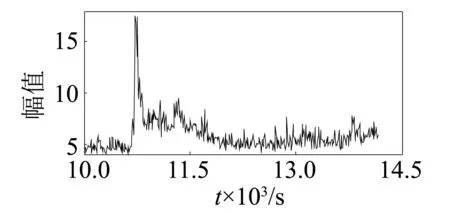
图10 脉冲系数Fig.10 Impulse factor

图11 外圈特征频率Fig.11 Feature frequency of outer race

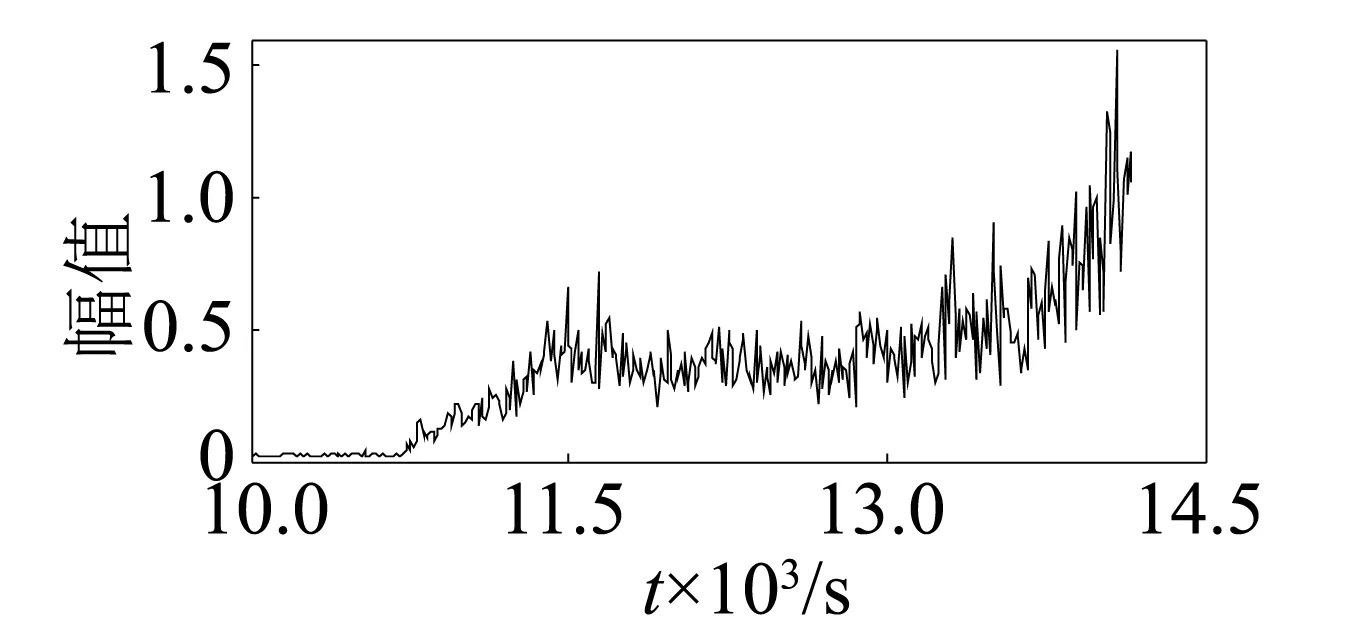
图12 内圈特征频率Fig.12 Feature frequency of inner race

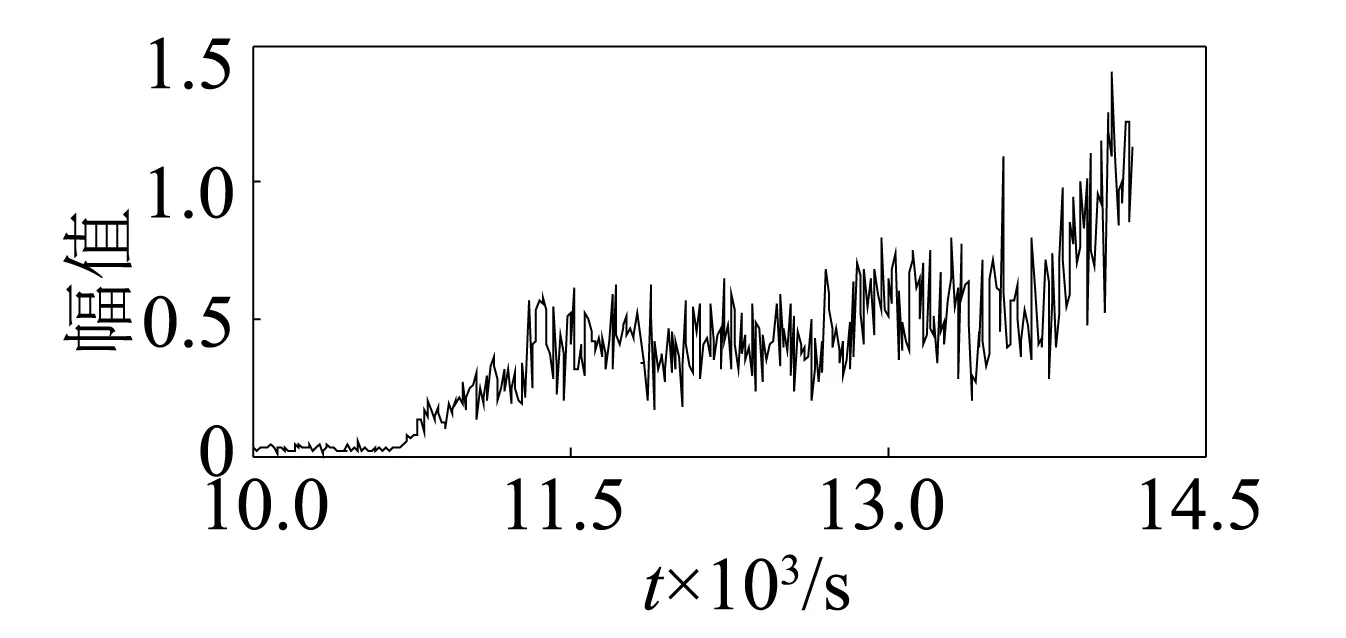
图13 滚动体特征频率Fig.13 Feature frequency of ball

图14 保持架特征频率Fig.14 Feature frequency of cage

应用式(16)和式(17)对以上13个特征参数以及IEEE PHM 2012中的其它3组实验数据进行早期故障敏感性分析，如表1所示。

通过第1组实验数据的敏感性可知，13个特征参数敏感性由高到低依次为：峭度、波峰因子、裕度因子、脉冲系数、形状系数、偏度、峰值、外圈特征频率、滚动体特征频率、保持架特征频率、平均值、均方根。根据第1组实验数据的敏感性及其变化趋势可以看出，敏感性较高的峭度、波峰因子、裕度因子、脉冲系数、形状系数前5个特征参数(图6～图10)在轴承出现初始故障时其幅值快速增大，变化非常明显，其它特征参数在初始故障期间变化比较平稳。

通过表1可知，其它3组实验中峭度、波峰因子、裕度因子、脉冲系数、形状系数5个特征参数的敏感性排列在前5名，其敏感性高且稳定性好。在滚动轴承初始故障检测过程中，如果增加特征参数，其马氏距离可能在初始故障时变化不明显；减少特征参数数目，其马氏距离可能在初始故障时幅值减小。因此，在滚动轴承初始故障预测过程中，使用峭度、波峰因子、裕度因子、形状系数、脉冲系数5个特征参数构建马田系统的基准空间，用于检测滚动轴承的初始故障是合理的。

表1 特征参数早期故障的敏感性Tab.1 Sensitivity of features in incipient fault

2.3 滚动轴承退化状态特征参数选择

2.3.1 相关性分析

相关性分析可以判断两个特征之间的相互联系或相互依赖关系。根据特征参数与轴承退化状态的相关性，选择与轴承退化状态相关性较大的特征参数作为检测轴承退化状态的特征参数构建马田系统的基准空间。相关性分析选择的特征参数更加符合轴承的退化状态，避免了其它特征参数的影响，对于准确判断轴承的退化状态有重要意义。

两个长度相同的向量A=(A1,A2,…,Am)和B=(B1,B2,…,Bm)之间的相关性可以通过如下公式计算：

(18)

2.3.2 特征参数选择

滚动轴承从开始到失效经历了四个阶段：滚动轴承无故障阶段、滚动轴承轻微故障阶段、滚动轴承严重故障阶段和滚动轴承失效阶段。滚动轴承退化状态评估中，构造一个合适的特征参数最为重要，该参数应该随着故障的发展而不断增大且变化规律符合轴承的退化状态，才能更好的利用其变化规律监测轴承的运行状态。

滚动轴承状态监测特征参数选择过程中，根据13个特征参数为基准空间的马氏距离MD(图15)和13个特征参数的变化趋势(图2～图14)可以看出，MD的变化趋势更加符合轴承的退化状态，其变化趋势与轴承的性能退化状态有很好的相关性。滚动轴承状态监测特征参数优化过程中，将马氏距离MD作为轴承退化状态的基准，分析13个特征参数与马氏距离MD的相关性，选择相关性较大的特征参数作为马田系统的基准空间，根据优化后马氏距离的变化趋势，判断轴承的退化状态。

为了验证特征参数在不同实验中特征参数与退化状态的相关性，使用IEEEPHM2012中6组试验数据，分析13个特征参数与其马氏距离的相关性，其结果如表2所示。

图15 马氏距离MDFig.15 Mahalanobis distance MD

通过表2可知：平均值、均方根、峰值和滚动轴承4个特征频率幅值的7个特征参数与其马氏距离的相关性高且稳定性好。经过相关性分析降低了马田系统基准空间的维度，分析得出的7个特征参数比原始13个特征参数数量更少，其特征参数的变化趋势更加符合轴承的退化状态。因此，在滚动轴承状态监测过程中，使用平均值、均方根、峰值和滚动轴承4个特征频率幅值的7个特征参数构建马田系统的基准空间，用于检测滚动轴承初始故障是合理的。

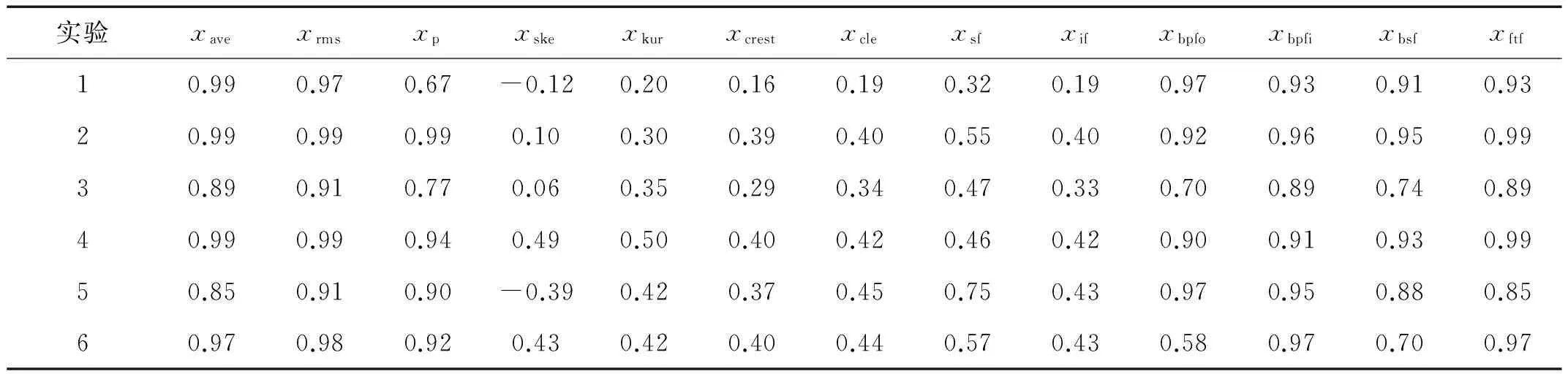
表2 特征参数与马氏距离的相关性Tab.2 Correlation of feature and MDs

3 实验验证和讨论

3.1 案例1

3.1.1 滚动轴承初始故障检测

为了验证峭度、波峰因子、裕度因子、形状系数、脉冲系数5个特征参数作为马田系统基准空间时检测初始故障的准确性。分别采用实验中全部13个特征参数和峭度、波峰因子、裕度因子、形状系数、脉冲系数5个特征参数作为马田系统的基准空间，其两组特征参数的马氏距离MD和MD1的变化趋势，如图16所示。

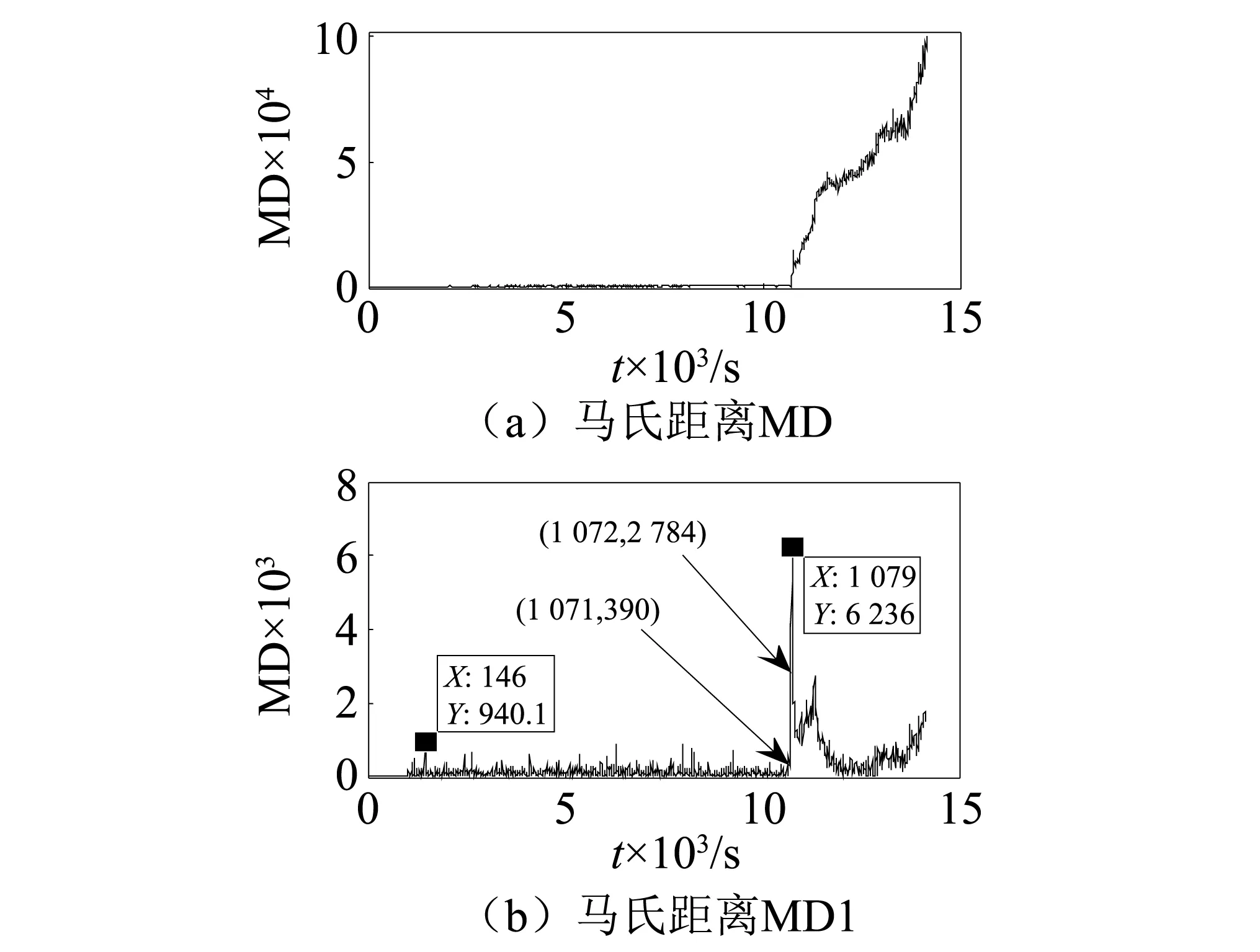
图16 两种马氏距离的比较Fig.16 Comparison of two MDs

通过图16中马氏距离MD和MD1变化趋势可知，马氏距离MD1在1 072处幅值明显增大，达到2 784，高于前期最大值940.1，并且在1 079处达到最大值6 236，在1 084处减小到1 074。根据马氏距离的变化趋势可以判断，轴承在该时段出现了早期故障，其马氏距离在故障初始阶段达到了最大值，其变化趋势比马氏距离MD的变化趋势更加明显，用于检测轴承的初始故障更加有效。因此，用敏感性分析确定的特征参数比原始特征参数数目更少，降低了马田系统基准空间的维度，优化后特征参数的马氏距离其识别初始故障的能力更强。

3.1.2 滚动轴承状态监测

为了进一步验证平均值、均方根、峰值和滚动轴承内圈特征频率、外圈特征频率、滚动体特征频率、保持架特征频率7个特征参数作为马田系统基准空间时监测轴承状态的准确性，分别采用实验中全部13个特征参数和相关性优化后的7个特征参数作为马田系统的基准空间，其两组特征参数的马氏距离MD和MD2的变化趋势，如图17所示。为了进一步观察马氏距离在状态改变时的变化趋势，将轴承第二阶段到第三阶段时的变化趋势局部放大，如图17所示。滚动轴承状态改变时，其各点幅值及状态改变量，如表3所示。

表3 第3阶段的状态改变量Tab.3 Condition changes of stage 3

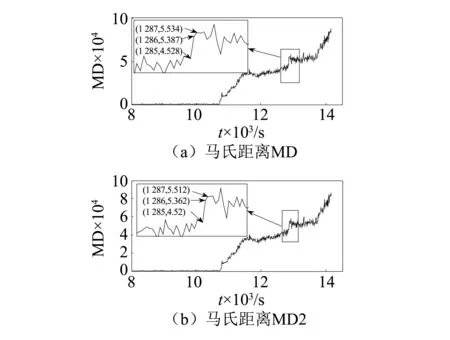
图17 马氏距离MD和MD2的比较Fig.17 Comparison of MD and MD2

通过图17可知，马氏距离MD和MD2的变化趋势比较接近，并且其相关性为99.9%。在状态改变时，用1287样本的幅值和1285样本幅值的差值定义为状态改变量，在状态改变时MD的改变量为1.006，MD1的改变量为0.992，MD的改变量比MD2的改变量多0.014，占MD改变量的1.4%。

根据相关性分析优化的特征参数和状态改变量可以看出，优化后的7个特征参数比原始13个特征参数减少了6个，特征空间维度降低了46%，而优化后马氏距离的状态改变量与原始马氏距离的改变量只差1.4%，并且其马氏距离变化趋势非常相似，优化后的特征参数构建的马田系统完全可以代替原始特征参数构建的马田系统。

通过应用相关性分析优化后的7个特征参数构建马田系统基准空间，其马氏距离MD2的变化趋势能准确的判断轴承的退化状态，其寿命的四个阶段比较明显，其各个阶段变化趋势，如图18所示。

图18 马氏距离MD2Fig.18 Mahalanobis distance MD2

根据MD2的变化趋势和轴承四个阶段的特点，滚动轴承的四个阶段分别为：第1阶段1～1 071；第2阶段1 072～1 374；第3阶段：1 375～1 285；第4阶段：1 286～1 416。

3.2 案例2

为了验证该方法在其它轴承以及其它环境中的有效性，本文采用了Intelligent Maintenance Systems提供的数据IMS Bearing Data，该实验所使用试验平台，如图19所示[24]。试验用的测试轴承为Rexnord ZA-2115 双列球轴承。试验中，数据采样频率为20 kHz，轴承转速为2 000 r/min，每次采样间隔为10 min，采样时间为1 s，每个样本含有20 480个数据点，试验样本为1 991个。

图19 轴承测试台Fig.19 Bearing test rig

根据滚动轴承初始故障检测和状态监测时的特征参数，分别应用IMS Bearing Data，将滚动轴承初始故障敏感性较高的峭度、波峰因子、裕度因子、形状系数、脉冲系数5个特征参数和滚动轴承退化状态相关的平均值、均方根、峰值和滚动轴承4个特征频率幅值的7个特征参数分别作为马田系统的基准空间进行滚动轴承初始故障检测和状态监测，结果如图20所示。从图20(a)可知，由峭度、波峰因子、裕度因子、形状系数、脉冲系数构成马田系统基准空间的马氏距离MD1在1667个样本中出现了早期故障，其变化趋势在初始故障阶段比较明显，可以检测轴承的初始故障。从图20(b)可知，由平均值、均方根、峰值和滚动轴承4个特征频率幅值的7个特征参数构成马田系统基准空间的马氏距离中，可以明显的看出滚动轴承寿命发展的四个阶段，各阶段变化比较明显，适合用于监测轴承的退化状态。

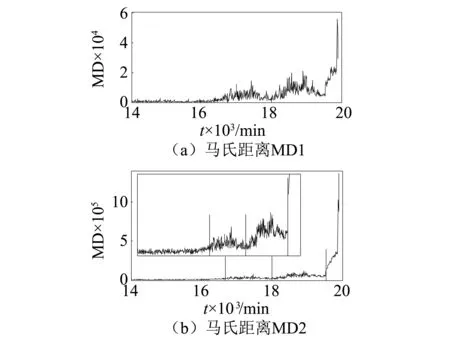
图20 两种马氏距离的性能退化比较 Fig. 20 Performance degradation comparison of two MDs

综上所述，本文提出的基于马田系统的初始故障检测和状态监测的方法可以准确有效的判断出轴承的初始故障和退化状态。运用敏感性分析和相关性分析优化马田系统基准空间的特征参数，优化后的特征参数其变化趋势更加符合轴承的初始故障和退化状态的特点，根据马氏距离的变化趋势可以准确判断出轴承的初始故障和轴承寿命的四个阶段。

马田系统在滚动轴承状态监测过程中，由于故障具有复杂性和多变性，部分轴承故障畸形发展和演化，其特征参数变化不规则，状态监测过程中马田系统还有一定的不足，需要进一步的研究，克服这些缺点。

4 结 论

基于马田系统的滚动轴承早期故障检测和状态监测中，通过特征参数早期故障敏感性分析和退化状态的相关性分析，得出了轴承早期故障敏感的特征参数和退化状态相关的特征参数，去除了其它特征参数的影响。运用马田系统将两组特征参数融合为单一的特征参数：马氏距离，根据马氏距离的变化趋势，判断轴承的初始故障和退化状态。通过两个实验，验证了该方法在早期故障检测和状态监测中的有效性和准确性。

[1] LEE J, WU F J, ZHAO W Y, et al. Prognostics and health management design for rotary machinery systems—Reviews, methodology and applications [J]. Mechanical Systems and Signal Processing, 2014, 42(1/2): 314-334.

[2] 佟佩声. 滚动轴承变工况条件下静电监测特征提取及故障程度识别方法研究[D]. 南京：南京航空航天大学，2014.

[3] PATIL M S. MATHEW J, RAJENDRAKUMAR P K. Bearing signature analysis as a medium for fault detection a review[J]. Journal of Tribology, 2007，130(1)： 14001-14007.

[4] ZHAO X M, ZUO M J, PATEL T. EMD, ranking mutual information and PCA based condition monitoring [C]∥ Proceedings of the ASME 2010 International Design Engineering Technical Conferences & Computers and Information in Engineering Conference. Montreal, Canada, 2010 .

[5] SHAKYA P, MAKARAND S K, DARPE A K. A novel methodology for online detection of bearing health status for naturally progressing defect [J]. Journal of Sound and Vibration, 2014, 333(21): 5614-5629.

[6] SHAKYA P, MAKARAND S K, DARPE A K. Bearing diagnosis based on Mahalanobis-Taguchi-Gram-Schmidt method[J]. Journal of Sound and Vibration, 2015, 337: 342-362.

[7] YU Jianbo. Health condition monitoring of machines based on hidden markov model and contribution analysis [J]. IEEE Transactions on Instrumentation and Measurement, 2012, 61(8): 2200-2211.

[8] WANG Zhipeng, LU Chen, WANG Zili, et al. Fault diagnosis and health assessment for bearings using the Mahalanobis-Taguchi system based on EMD-SVD [J]. Transactions of the Institute of Measurement and Control, 2013, 35(6): 798-807.

[9] 余发军，周凤星，严保康. 基于字典学习的轴承早期故障稀疏特征提取[J]. 振动与冲击，2016，35(6):181-186. YU Fajun, ZHOU Fengxing, YAN Baokang. Bearing initial feature extraction via sparse representation based on dictionary learning[J]. Journal of Vibration and Shock, 2016, 35(6):181-186.

[10] LIM R, KEONG C, MBA D. Bearing time-to-failure estimation using spectral analysis features [J]. Structural Health Monitoring, 2014, 13(2): 219-230.

[11] HU Jinqiu, ZHANG Laibin, LIANG Wei. Dynamic degradation observer for bearing fault by MTS-SOM system[J]. Mechanical Systems and Signal Processing, 2013, 36 (2): 385-400.

[12] SOYLEMEZOGLU，JAGANNATHAN S，SAYGIN C. Mahalnobis Taguchi System (MTS) as a prognostic tool for rolling element bearing failures[J]. Journal of Manufacturing Science & Engineering, 2010, 132(5):635-645.

[13] SHEN Zhongjie, HE Zhengjia, CHEN Xuefeng, et al. A monotonic degradation assessment index of rolling bearings using fuzzy support vector data description and running time [J]. Sensors, 2012, 12(8): 10109-10135.

[14] ZHU Xiaoran, ZHANG Youyun, ZHU Yongsheng. Bearing performance degradation assessment based on the rough support vector data description [J]. Mechanical Systems and Signal Processing, 2013, 34 (1/2): 203-217.

[15] YAN Changfeng, YOU Li, KONG Yuanyuan, et al. A hybrid method to estimate initial faulty time of rolling bearing [J]. International Conference on Control System and Automation, 2013, 8(9): 474-480.

[16] KANG M, KIM J, KIM J M. Reliable fault diagnosis for incipient low-speed bearings using fault feature analysis based on a binary bat algorithm [J]. Information Sciences, 2015, 294: 423-438.

[17] BHENDE A R, AWARI G K, UNTAWALE S P. Comprehensive bearing condition monitoring algorithm for incipient fault detection using acoustic emission [J]. Jurnal Tribologi, 2014(2): 1-30.

[18] WANG Zhipeng, WANG Zili, TAO Laifa, et al. Fault diagnosis for bearing based on Mahalanobis-Taguchi System [C]∥ 2012 Prognostics and System Health Management Conference. Denver, USA, 2012.

[19] ELHAM A. Mahalanobis Taguchi system: a review [J]. Emerald Insight, 2015, 32(3): 291-307.

[20] 任江涛，蔡远文，史建伟，等. 基于马田系统的设备健康监测技术研究[J]. 计算机测量与控制，2012，20(3): 634-641. REN Jiangtao, CAI Yuanwen, SHI Jianwei, et al. Research on equipment health monitoring using Mahalanobis-Taguchi system [J]. Computer Measurement and Control, 2012, 20(3): 634-641.

[21] 何正嘉，陈进，王太勇，等. 机械故障诊断理论及其应用[M]. 北京：高等教育出版社，2010.

[22] BRIAN P G, KEN S. Rolling element bearing analysis[J]. Materials Evaluation, 2011, 70(1): 78-85.

[23] NECTOUX P, GOURIVEAU R, MEDJAHER K, et al. PRONOSTIA: An experimental platform for bearings accelerated life test [C]∥ IEEE International Conference on Prognostics and Health Management. Denver, USA, 2012.

[24] LEE J, QIU H, YU G, et al. Rexnord technical services: bearing data set [EB/OL].http:∥ti.arc.nasa.gov/tech/dash/pcoe/prognostic-data-repository/, 2007.

Incipient fault detection and condition monitoring of rolling bearings by using the Mahalanobis-Taguchi System

YAN Changfeng1, ZHU Tao1, WU Lixiao1, AHMED Y Y1, GUO Jianfeng2

(1.School of Mechanical and Electrical Engineering, Lanzhou University of Technology, Lanzhou 730050, China;2. Lanzhou Uranium Enrichment Company of China Nuclear Industry Corporation，Lanzhou 730060，China)

Because the sensitivity of feature parameters of vibration signal are different with the four-stage of bearing life, the sensitivity to incipient fault and the correlation of degradation condition were analyzed in this work. A new method of incipient fault detection and performance degradation was presented by the Mahalanobis-Taguchi System (MTS). The feature parameters which were sensitive to incipient fault and related performance degradation condition were treated as a reference space for the Mahalanobis-Taguchi System (MTS). Two groups of feature parameters were fused with single feature parameters in MTS of Mahalanobis distance. Since MD1 is more sensitive to incipient fault of bearings, it was used to detect the time of incipient fault during the first and second stages of bearing life. According to MD2 increasing with performance degradation, the degradation state of bearings was estimated by variation tendency. By using this method, the uncertainty and instability of single feature parameters could be avoided in different running condition. The incipient fault was also detected accurately and degradation condition of bearings life was distinguished. The validity and accuracy of this method were verified by the service life of rolling bearing in an accelerated life test.

Mahalanobis-Taguchi System (MTS); rolling bearing; incipient fault; condition monitoring; correlation

国家自然科学基金项目(51165018)

2015-12-14 修改稿收到日期： 2016-05-09

剡昌锋 男，博士，研究员，1974年生

TH133

A

10.13465/j.cnki.jvs.2017.12.026