磁流变液润滑浮环轴承及其在转子振动控制中的应用

王小虎， 陆 雯， 李鸿光， 孟 光

(上海交通大学 机械系统振动与噪声国家重点实验室，上海 200240)

磁流变液润滑浮环轴承及其在转子振动控制中的应用

王小虎， 陆 雯， 李鸿光， 孟 光

(上海交通大学 机械系统振动与噪声国家重点实验室，上海 200240)

利用自制磁流变液及其可控简单、成本低等优点，提出了一种使用磁流变液润滑的可控浮环轴承。采用Herschel-Bulkley模型对包含剪切稀化效应的磁流变液剪切特性进行了建模；通过自制的磁流变仪测试系统测试并识别了所制磁流变液的模型参数；利用识别的参数分析了磁流变液润滑浮环轴承的动态特性及可控性；分析了采用此种轴承的转子系统的抑振效果。结果表明，磁流变液润滑浮环轴承在外加磁场后有较好的振动抑制作用。同时，相较于磁流变液润滑普通滑动轴承，磁流变液润滑浮环轴承有更好的抑振效果，且减小了轴颈摩擦力矩，降低了摩擦功耗。

磁流变液；浮环轴承；转子系统；振动控制

磁流变液(Magnetorheological fluid)作为一种智能材料，因其较快的响应速度(ms级)及较强的性质(黏度)改变能力而被广泛应用于各种场合的振动控制中。近年来，在转子振动控制中，磁流变液主要应用于挤压油膜阻尼器。对于滚动轴承支撑的转子系统，采用磁流变液阻尼器并改变外加磁场强度，可以调节阻尼器阻尼，从而实现半主动控制[1-2]。对于采用滑动轴承的转子系统，研究更多集中于使用“智能轴承”，即让磁流变液充当润滑剂，通过磁场改变其性质，从而改变轴承性质。Hesselbach等[3]首先将磁流变液作为润滑剂用于静压轴承中，使其刚度和响应速度均比普通静压轴承获得了提升；Urreta等[4]分别测试了磁流变液和铁流体充当润滑剂时普通滑动轴承的可控性，发现在外加磁场后，磁流变液润滑轴承性能改变高于铁流体润滑轴承；Gertzos等[5]借助商用CFD软件，分析了磁流变液在润滑过程中的流变现象，其结果与更早的Tichy[6]采用简化模型得出的结果相吻合；Bompos等[7]研究了磁流变液在滑动轴承润滑中作用，发现其能显著改变轴承的刚度和阻尼特性。由于转子本身在进行旋转运动，因此对于转子系统的控制方法主要采用半主动控制，即调节转子的支撑刚度和阻尼，从而改变转子的临界转速、减小振幅等。上述各研究均采用此种方法。

对磁流变液的建模，特别在实际应用中，常采用现象学模型(Phenomenological model)。此类模型从磁流变液的剪切率-剪应力测试关系出发，通过较为简单的模型来描述磁流变液的性质，其中最常用的是Bingham模型。此模型认为，在达到屈服应力前，磁流变液行为近似刚体；而超过屈服应力后，磁流变液将呈现牛顿流体的性质，即黏度恒定。然而在实际测试中，磁流变液屈服后往往并不表现出牛顿流体的行为，而是会随着剪切率升高出现黏度降低，即所谓剪切稀化的现象[8]。对于磁流变液润滑轴承，由于润滑油膜极薄，在油膜转速较高时，强烈的剪切稀化效应将导致磁流变液性能下降从而降低可控性。此现象被Urreta等观察到，故该论文认为磁流变液润滑轴承只适用于低速场合。另一方面，在外加磁场后，由于铁粉的存在，磁流变液将对轴颈表面产生较大摩擦，从而导致能耗增高。上述两特性在磁流变液作为润滑剂时会产生不利影响，因此应当尽可能减轻。

为了克服上述不利影响同时保持磁流变液润滑轴承的可控性，本文提出了一种磁流变液润滑的浮环轴承，能在一定程度上减小剪切率、降低轴径摩擦力矩。同时，为了包含剪切稀化效应，研究采用了Herschel-Bulkley模型，分析了浮环轴承中磁流变液的润滑情况。最后，文章对此种轴承的转子系统进行了仿真，对比了磁流变润滑浮环轴承与一般轴承的振动抑制特性。

1 浮环轴承的非牛顿流体润滑

1.1 磁流变液润滑理论

为弥补前述Bingham模型对剪切稀化现象描述的缺失，本文采用Herschel-Bulkley(HB)模型引入剪切稀化效应，对磁流变液进行建模。HB模型中液体剪切率与剪应力有如下关系：

(1)

(2)

(3)

(4)

图1 润滑油膜几何结构及本地坐标系Fig. 1 Lubrication oil film and local coordinate system

1.2 浮环轴承结构及润滑

图2为浮环轴承的几何结构图。图2中Oj，Or和Ob分别是轴径、浮环及轴承几何中心；φ1, φ2,e1, e1是此三个几何中心的相对位置参数，它们共同决定了轴颈、浮环及轴承的相对姿态。图2(b)和图2(c)分别是内外油膜的放大图，其中s为浮环表面速度，t为轴颈表面速度，下标1对应由转动引起的速度，下标2、下标3分别对应轴心变位速度在垂直于偏心矢量和平行于偏心矢量上的两个分量，上标i,o标明变量属于内或外油膜。

图2 浮环轴承结构及位置关系Fig. 2 Geometry of a floating ring bearing

对于外油膜有

(5)

(6)

对于内油膜有

(7)

(8)

求解以上各式，可得到油膜压力分布；再积分可得到油膜力。浮环转速ωr可通过假定浮环受力平衡，即浮环内外表面摩擦力矩相等：

(9)

式中：L为轴承宽度。同时，内外油膜力Fi与Fo也相互平衡，即Fo=Fi+Gr，Gr为浮环重量。

2 磁流变液性质测量及参数识别

由于现有商用磁流变液多是为直线阻尼器设计，以硅油为基液，铁粉含量偏高(质量分数>70%)，不适合用作润滑剂。因此作者以32#透平油(ISOVG32)为基液，配制了质量分数30%的磁流变液，并设计了磁流变仪测试系统，识别得到了在不同励磁电流下自制磁流变液的HB模型参数。测试系统，如图3所示，主要部件包括剪切室、伺服电机系统、扭矩传感器、励磁线圈及信号采集系统等。系统核心为剪切室，其主要组成部分为可旋转的滚筒及剪切室壁。滚筒由伺服电机带动旋转，滚筒与剪切室壁之间有0.25mm间隙，其间充满待测磁流变液。滚筒旋转后，转矩通过磁流变液传递到剪切室壁，而剪切室壁连接扭矩传感器，通过控制电机转速以及采集扭矩传感器信号，利用剪切室几何尺寸可以换算出磁流变液的剪切率和剪应力。同时，剪切室外的励磁线圈，同时，通过控制剪切室外的励磁线圈中的励磁电流强度，可以获得不同强度的磁场。得到剪切率和剪应力后，通过非线性回归方法得到HB模型参数。

图3 磁流变仪及测试系统Fig. 3 Magnetorheometer and test system scheme

本研究中线圈采用4个磁极90°均匀分布，南北极间隔排列。为了获得剪切室中磁场强度，需对磁场进行测量。由于剪切室间隙只有0.25mm，无法放置探头，故将剪切室拆卸，只留剪切室壁，测试系统，如图4所示。剪切室壁由铝合金制造，滚筒和轴由奥氏体不锈钢制造，它们磁导率与空气基本相同，都可看作非导磁物质，故作者认为，在图4所示系统中测得的磁场强度与完整剪切室中的磁场分布相同。从图4可知，剪切室中油膜处周向磁场呈规律分布，且测试结果与仿真分析结果相符较好。由此定义油膜中等效磁场强度，即将油膜中周向磁场作平均处理，得到相应电流强度下的等效磁场强度H，如表1所示。

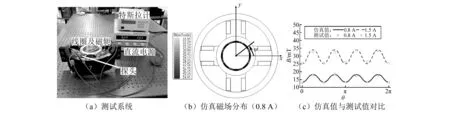
图4 线圈磁场测试系统及仿真-测试结果对比Fig. 4 Coil magnetic field test system and comparison of simulated and tested results表 1 识别的磁流变液HB模型参数Tab. 1 Identified HB model parameters

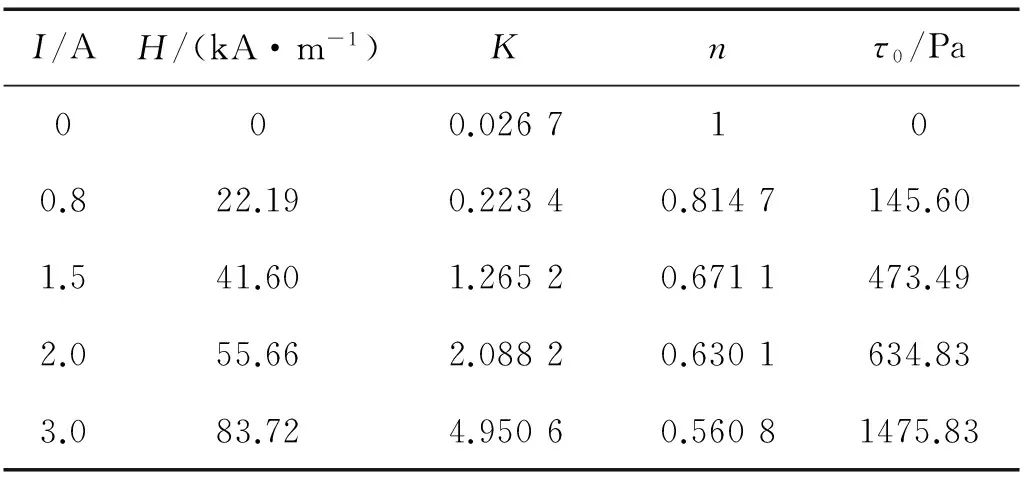
I/AH/(kA·m-1)Knτ0/Pa000.0267100.822.190.22340.8147145.601.541.601.26520.6711473.492.055.662.08820.6301634.833.083.724.95060.56081475.83

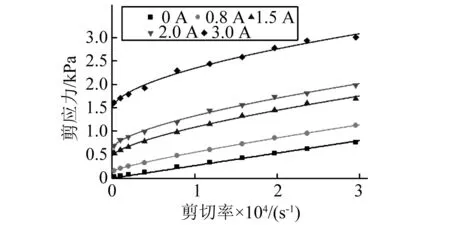
图5 磁流变液剪切率-剪应力关系Fig. 5 Shear rate-stress relationship of MRF

图6 磁流变液HB模型参数Fig. 6 Identified HB model parameters of MRF

3 磁流变液润滑浮环轴承特性

3.1 浮环转速及轴颈摩擦力矩

应用前述理论与识别后的HB模型，可以计算磁流变液润滑浮环轴承的特性。计算中使用的参数为：轴颈半径30mm，浮环厚度8mm，轴承长度60mm，内间隙0.1mm，外间隙0.2mm。首先对磁流变轴承中磁场进行仿真，如图7所示。可见，轴承内外油膜中磁场强度不同，且内油膜中磁场强度大大低于外油膜，根据图5测试结果，可以假设内油膜中磁流变液为牛顿流体。

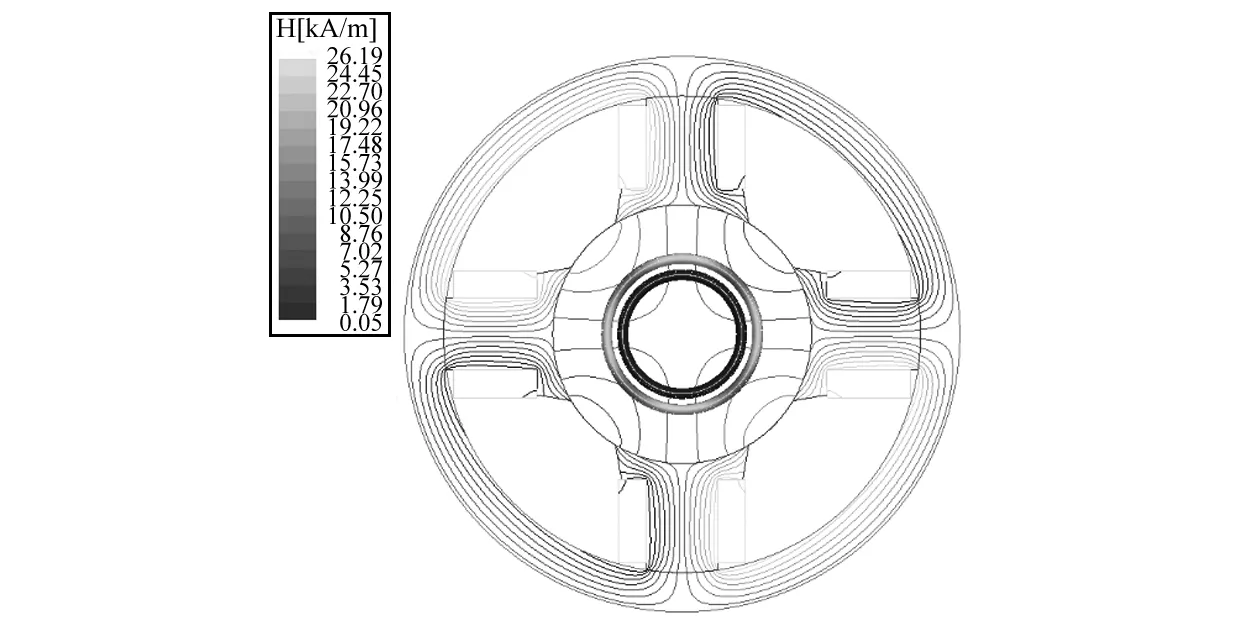
图7 浮环内外油膜中磁场对比(I=1.5 A)Fig. 7 Comparison of outer-inner oil film magnetic field (I=1.5 A)

内外磁场强度差别大使得外油膜对浮环摩擦力矩增大，其直接结果是浮环转速降低。图8绘制了浮环转速随外偏心变化的规律曲线。选择外偏心作为参考，是因为浮环转速低于轴转速，因此轴承承重主要由外油膜决定，而外偏心则可以刻画外油膜的承重能力。较低的浮环转速可以降低外油膜中的剪切率，部分地克服磁流变液的剪切稀化效应。同时，内油膜中由于磁场强度低，其对轴颈的摩擦力矩也较低。

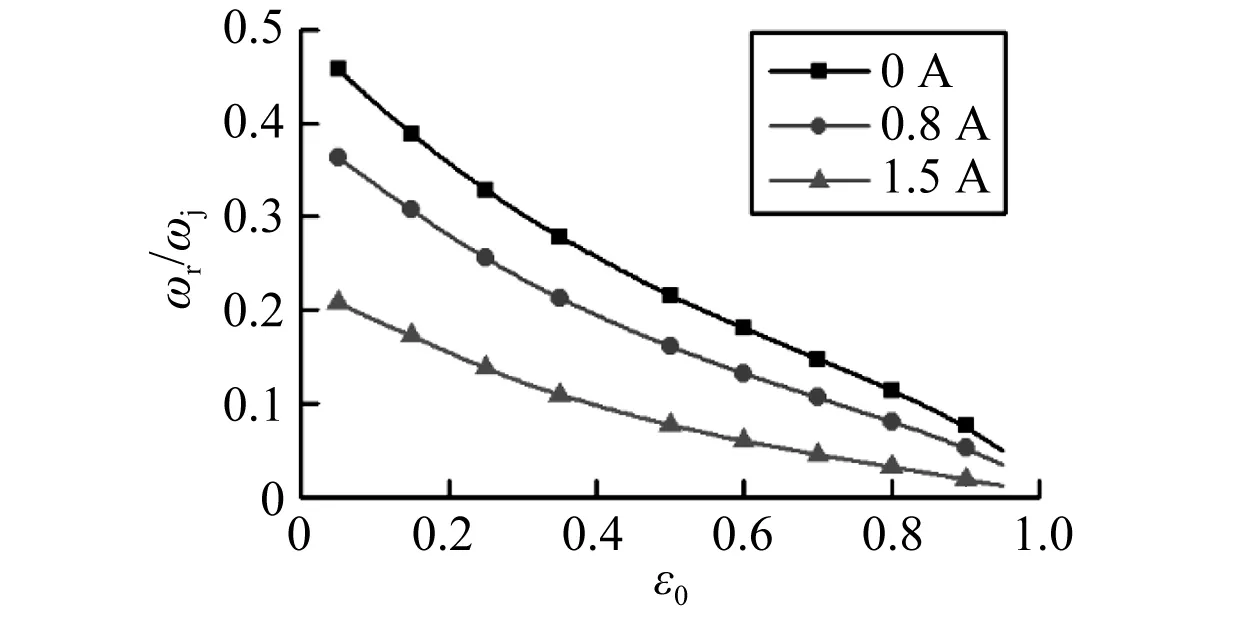
图8 浮环与轴转速比随外偏心变化曲线Fig. 8 Speed ratio of floating ring to journal versus outer eccentricity ratio

为了验证此效果，选取了三种不同的轴承作为对比。这三种轴承分别为：采用32号透平油的普通滑动轴承(B1)、采用磁流变液的普通滑动轴承(B2)以及采用磁流变液的浮环轴承(B3)，同时磁流变液均处于1.5A励磁电流磁场中。普通滑动轴承间隙为0.2mm，长度也为60mm。图9描绘了轴转速3 000r/min时采用这三种轴承不同时轴颈的摩擦力矩。可以看到，B2对轴颈施加了最大的摩擦力矩，而B3对轴颈的摩擦力矩最小，甚至小于用32号透平油润滑的B1。这是因为浮环轴承内油膜中磁场强度低，且轴颈对浮环的相对转速低于轴颈转速，使得这种情况下轴颈摩擦力矩较小，可改善采用磁流变液润滑而导致的温度及能耗升高等缺点。

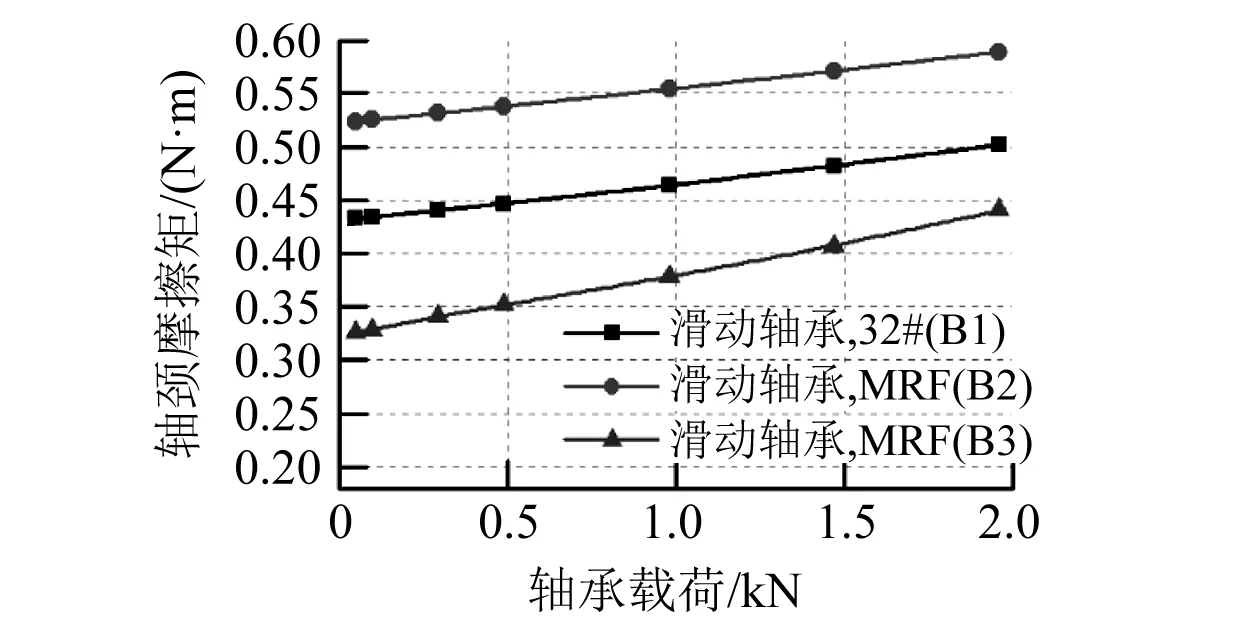
图9 三种轴承及润滑液下轴颈摩擦力矩Fig. 9 Journal friction torque of three types of bearings

3.2 刚度与阻尼特性

(10)

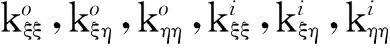
4 轴承-转子系统仿真分析

为验证磁流变液润滑轴承改变轴承阻尼的能力在抑制转子振动方面的效果，本文用有限元方法对图12所示转子系统进行振动分析。转子系统采用悬臂梁结构，轴长800mm，轴径80mm，悬臂端有一钢质质量盘(密度7 800kg/m3)，半径160mm，厚度15mm。浮环轴承位于距悬臂端160mm处，轴颈60mm，轴另一端用滚动轴承支撑。整个轴用10个Timoshenko梁单元建模，圆盘等效为等质量、 转动惯量及惯性矩的质量单元。由于滚动轴承刚度较高且不是本研究关注对象，故将其等效为铰接约束。浮环轴承内外油膜分别用刚度-阻尼单元建模，而浮环本身忽略其转动影响，等效为质量单元mr。因此模型共有13个节点，其中节点11的3个移动自由度被约束，节点13的所有自由度被约束；模型由16个单元，其中10个梁单元，2个质量单元，2个弹簧单元及2个阻尼单元。浮环轴承参数与前述相同，且此时承载164.93N。

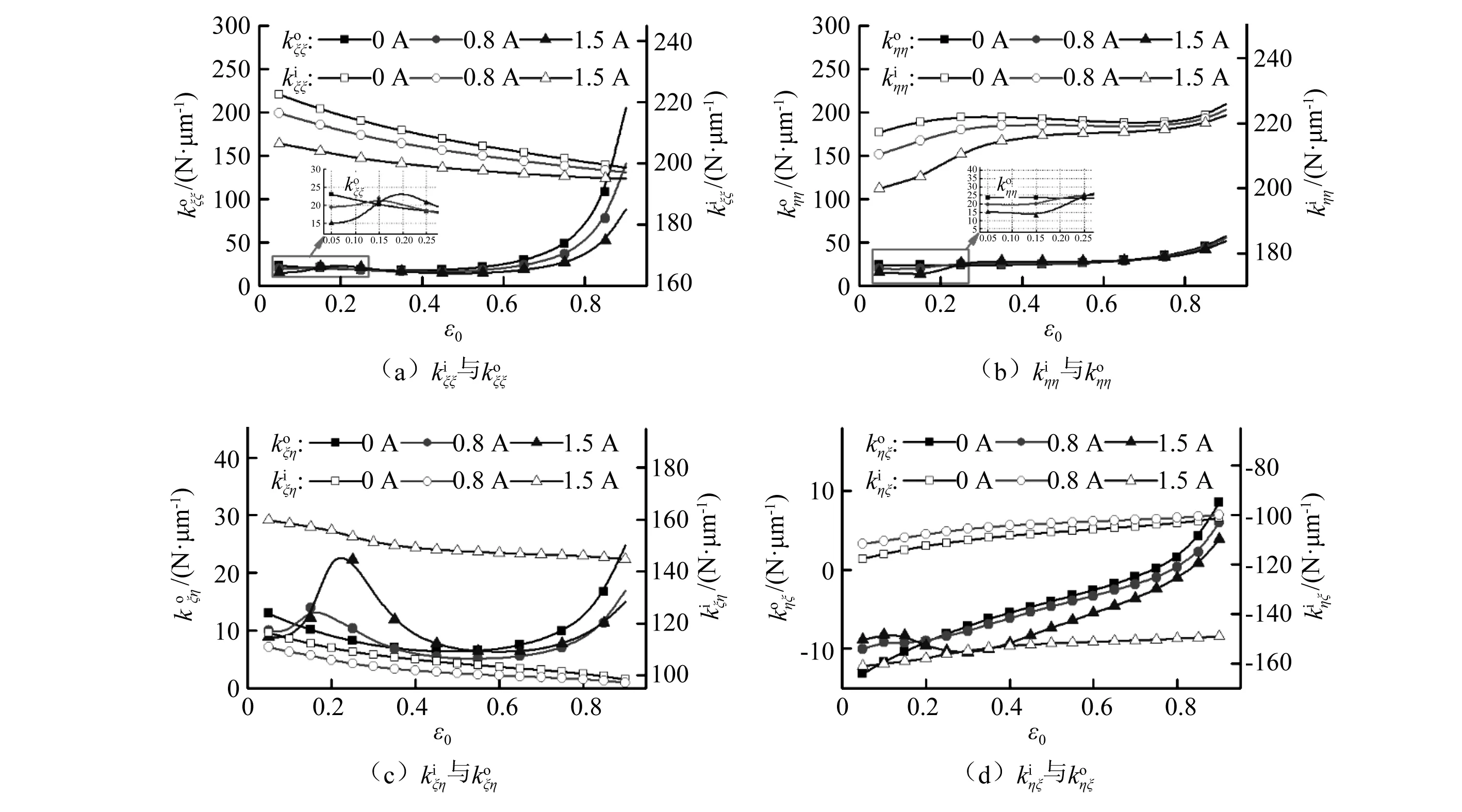
图10 磁流变液润滑浮环轴承内外油膜刚度系数随外偏心εo变化规律Fig. 10 Inner and outer stiffness coefficients of MRF lubricated FRB versus outer eccentricity ratio

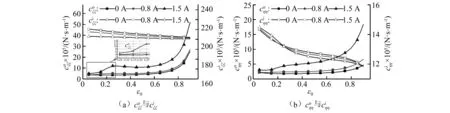
图11 磁流变液润滑浮环轴承内外油膜直接阻尼系数随外偏心εo变化规律Fig. 11 Inner and outer direct damping coefficients of MRF lubricated FRB versus outer eccentricity ratio

图12 转子系统几何模型及有限元模型Fig. 12 Geometry and finite element models of the rotor system

整个转子系统动力学方程的有限元格式可以写为：

([K]+[Ks]-[Me] Ω2)q=F

(11)式中：[M]为质量矩阵；Ω[Gb]与Ω[Gd]分别为梁和质量单元的回转矩阵，为反对称阵；[K]为梁单元刚度矩阵；[Ks]与[Cd]分别为表示油膜刚度阻尼的刚度矩阵与阻尼矩阵；[Me]为离心质量矩阵；Ω为轴转速；[Me] Ω2代表离心力引起的轴刚度软化效应；F为激励项；[C]为整体阻尼矩阵。此处通过结构阻尼的方式引入整体阻尼矩阵，即[C]=λ[K]，其中λ为结构阻尼比，取λ=0.02。

本研究主要分析转子为刚性转子时的动态行为，此时轴转速远低于轴临界转速。为考察转子的振动，假设圆盘处有0.02g·mm的偏心质量，将此偏心折算为简谐激励作为激励项F，用Newmark-Beta方法求解式(11)的瞬态解，可以计算出转子的轴心轨迹。图13为转子转速为3 000r/min时圆盘处的轴心轨迹。可见，当外加磁场后，转子振幅明显减小，且随着磁场强度的增加而进一步减小。同时，轴心轨迹程椭圆形，这是由于轴承刚度阻尼非对称导致的，此非对称性从图10、图11可知。

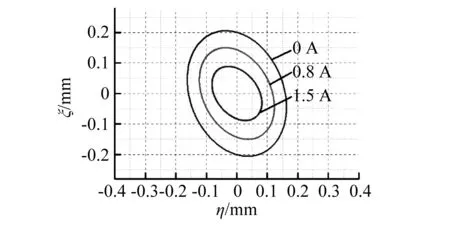
图13 转速3 000 r/min时圆盘轴心轨迹Fig. 13 Disk center orbits at 3 000 r/min

为说明用磁流变液润滑时浮环轴承相较于普通滑动轴承的优点，图14绘制了两种轴承在1.5A励磁电流磁场中轴端圆盘的轴心轨迹。从图14可知，此时用浮环轴承使得轴端的振动更小，而这是前述磁流变液剪切稀化效应导致的，因普通滑动轴承中剪切率较大。

图14 转速3 000 r/min时在1.5 A励磁电流下磁流变 液润滑浮环轴承和普通轴承圆盘轴心轨迹Fig. 14 Disk center orbits of MRF lubricated FRB and journal bearing at 3 000 r/min in magnetic field of I=1.5 A

5 结 论

磁流变液润滑浮环轴承外加磁场后，可以改变其

刚度阻尼特性，而其阻尼随磁场增强而升高。升高的阻尼特性可以降低轴的振动，起到抑制转子振动的作用。磁流变液的剪切稀化效应随磁场增强而增强，润滑油膜中因其剪切率较高，必须考虑剪切稀化效应。浮环轴承中的浮动环以低于轴转速转动，可以降低外油膜剪切率，有利于降低磁流变液剪切稀化作用的影响；同时内油膜因磁场强度低，对轴颈产生的摩擦力矩也较低，相较一般磁流变液轴承可以起到降低功耗的作用。

[1] 汪建晓, 孟光, 陈运西. 挤压式磁流变液阻尼器——转子系统的动力学特性与控制[J]. 机械工程学报, 2004, 40(3): 76-83.WANGJianxiao,MENGGuang,CHENYunxi.DynamicperformanceandcontrolofsqueezemodeMRfluiddamper—rotorsystem[J].ChineseJournalofMechanicalEngineering, 2004, 40(3): 76-83.

[2] 王修勇. 旋转剪切式磁流变液阻尼器设计及力学模型[J]. 振动与冲击, 2010, 29(10): 77-81. WANG Xiuyong. Design and mechanical model of a rotary-mode shear MR damper[J]. Journal of Vibration and Shock, 2010, 29(10), 77-81.

[3] HESSELBACH J, ABEL-KEILHACK C. Active hydrostatic bearing with magnetorheological fluid[J]. Journal of Applied Physics, 2003, 93(10): 8441-8443.

[4] URRETA H, LEICHT Y, SANCHEY A. Hydrodynamic bearing lubricated with magnetic fluids[J]. Journal of Intelligent Material Systems and Structures, 2010, 21: 1491-1499.

[5] GERTZOS K P, NIKOLAKOPOULOS P G, PAPADOPOULOS C A. CFD analysis of journal bearing hydrodynamic lubrication by Bingham lubricant[J]. Tribology International, 2008, 41(12): 1190-1204.

[6] TICHY J. Hydrodynamic lubrication theory for the Bingham plastic flow model[J]. Journal of Rheology, 1991, 35: 477- 496.

[7] BOMPOS D A, NIKOLAKOPOULOS P G. Rotordynamic analysis of a shaft using magnetorheological and nanomagnetorheological fluid journal bearings[J]. Tribology Transactions, 2016,59(1):108-118.

[8] BECNEL A C, HU W, WERELEY N M. Measurement of Magnetorheological fluid properties at shear rates of up to 25 000 s[J]. IEEE Transactions on Magnetics, 2012, 48(11): 3525-3528.

[9] WANG X, LI H, LI M. Dynamic characteristics of magnetorheological fluid lubricated journal bearing and its application to rotor vibration control[J]. Journal of Vibroengineering, 2015, 17(4): 1912-1927.

[10] SEE H. Field dependence of the response of a magnetorheological suspension under steady shear flow and squeezing flow[J]. Acta Rheologica, 2003, 42(1/2): 86-92.

A magnetorheological fluid lubricated floating ring bearingand its application to rotor vibration control

WANG Xiaohu, LU Wen, LI Hongguang, MENG Guang

(Key State Laboratory of Mechanical System and Vibration, Shanghai Jiao Tong University, Shanghai 200240, China)

A controllable floating ring bearing (FRB) lubricated with magnetorheological fluid (MRF) was proposed due to its controllability and low cost of the self-made MRF. The Herschel-Bulkley (HB) model was introduced to model the behavior of MRF under shear circumstances with the shear-thinning effect incorporated. A magnetorheometer was set up to measure the properties of the MRF and then the nonlinear regression method was adopted to identify the HB model parameters of the tested MRF. With these parameters, dynamic behaviors of the floating bearing along with its controllability of the rotor system was analyzed. Results demonstrate that the MRF lubricated FRB is capable of suppressing rotor vibration amplitudes. And compared to an MRF lubricated common journal bearing, the MRF lubricated FRB performances better in rotor vibration control, and bears a lower journal friction while maintaining the ability to alter dynamic characteristics.

magnetorheological fluid; floating ring bearing; rotor system; vibration control

国家自然科学基金(11427801；11372176)

2016-01-26 修改稿收到日期： 2016-05-09

王小虎 男，博士生，1986年生

李鸿光 男，博士，教授，1972年生

TH212；TH213.3

A

10.13465/j.cnki.jvs.2017.12.004