基于LMD频域近似熵频谱感知算法研究*

曾 旭，慕晓冬，王舒洋，赵 典

（火箭军工程大学，西安 710025）

基于LMD频域近似熵频谱感知算法研究*

曾 旭，慕晓冬，王舒洋，赵 典

（火箭军工程大学，西安 710025）

针对现有频域近似熵频谱感知技术在低信噪比条件下抗噪声性能和检测性能有待提升的问题，提出了一种基于LMD频域近似熵的频谱感知算法。①算法筛选出3个PF分量累加求和，使得算法提取局部调频包络特征信息得到最优，进一步排除噪声不确定度的影响。②算法对累加PF分量进行频域变换后求其近似熵，增强算法对频域信息的嗅探能力，提升算法检测性能。Monte Carlo仿真结果表明，在噪声不确定度为0 dB，采样点数为8 000的情况下，当信噪比大于-19 dB时，可以对2ASK信号达到100%的检测概率，与现有频域近似熵算法相比，检测性能约有17 dB的提升。

频域近似熵，频谱感知，噪声不确定度

0 引言

近年来，随着无线电技术的日益发展，无线电认知技术［1］在频谱资源的合理利用方面正起到越来越突出的作用，其核心技术是频谱感知。频谱感知能够对主用户信号的存在进行感知。而如何在低信噪比以及无主用户先验信息等条件下提升对主用户信号的检测性能，已经成为认知无线电信号处理领域的热点课题。

传统的频谱感知方法主要有匹配滤波器检测、能量感知法、循环平稳特征检测等［2-5］。匹配滤波器检测性能较优，但该方法复杂度较高，且需要主用户信号的先验信息。能量感知法复杂度低，实现较简单且不需先验信息，但其在低信噪比条件下的检测性能较低，受噪声不确定度影响较大。循环平稳特征检测性能优于匹配滤波器，但其计算量大，系统对信号的灵敏度不高。文献［6-8］运用基于香农熵的频谱感知算法，但是算法计算容易出现不收敛的现象，在低信噪比条件下对信号的检测性能不高。近似熵［9］（ApEn）和局部均值分解［10］（LMD）方法是一个理想的非线性指数，以其所需数据点较少、有较好的抗干扰能力且适用于非线性非平稳的随机信号、确定性信号或两种混合信号等特点被广泛运用于医学、生物学、机械设备故障诊断、语音信号端点检测等方面［11-13］。文献［14］将频域近似熵引入频谱感知中实现对调制信号感知，算法能实现对多种信号的感知，且无需先验信息复杂度小，但算法对噪声不确定性鲁棒性较差，且检测性能有待提升。受LMD近似熵对机械故障信号检测的启发，本文结合频域近似熵频谱感知优点对LMD筛选分量作频域变换后求近似熵值作为特征值进行频谱感知，在保留原有算法优势的同时，通过仿真实验与原有频域近似熵频谱感知算法检测性能进行对比，验证新算法抗噪声能力和检测性能。

1 算法描述

1.1 数学模型

频谱感知问题的数学模型，可通过假设检验确定［14］：

式中，x（n）表示接收信号，s（n）表示调制信号，w（n）表示高斯白噪声AWGN。在此设定：H0与H1不可同时出现，H0表示观测信号未检测出调制信号，H1表示检测出频段内出现调制信号。

频谱感知算法的目标就是能够以较高的正确率以及较低的误判决率来区别噪声信号以及低信噪比的调制信号。而调制信号的信息参数主要分布在时域、频域和相位域上，如果按照信息在不同域的相关性质，可对其分成3种情况，见图1。

图1 调制信号信息分布示意图

情况Ⅰ：只在某区域内进行信息感知，此时包括时域信息、频域信息以及相位域信息，3种区域内均含有不同的信息参数，如脉冲时间、脉冲宽度以及载波频率等。其中相较于时域上高斯白噪声对调制信号的影响，频域上调制信号的频谱规律性受干扰会相对小一些。数字调制信号的感知中，频域上的熵感知算法会较时域上的更灵敏一些。

情况Ⅱ：在每两个域的相关域内进行信息感知，其中时频相关域所含的信息最为丰富。

情况Ⅲ：在3个相关域内进行信息感知和参数提取。

1.2 LMD方法原理

LMD是一种对非线性非平稳信号自适应时频分析方法，它通过计算信号的局部极值点，通过循环迭代将原始信号分离为多个调频信号和包络信号PF分量，得到原始信号的时频分布图。

其算法过程如下：

①找出信号x（t）所有的局部极值点｛ni｝，确定x（t）的局部均值函数m11（t）和包络估计函数a11（t）：

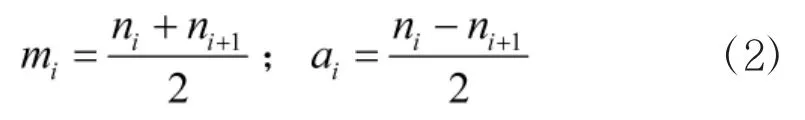
连接所有的点结合｛mi｝、｛ai｝，进行平滑处理，得到局部均值函数m11（t）和包络估计函数a11（t）。

②分离局部函数m11（t），得到一次处理函数h11（t）：

③解调一次处理函数h11（t）得到s11（t）：

将s11（t）作为x1（t），重复上述步骤，迭代至a1+n（t）约等于1，且，得到调频信号s1n（t）。

④确定LMD的第1个分量PF1（t）：

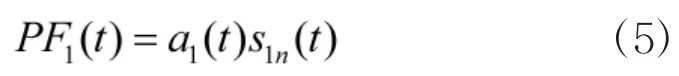
⑤确定LMD的所有分量PFi（t）：

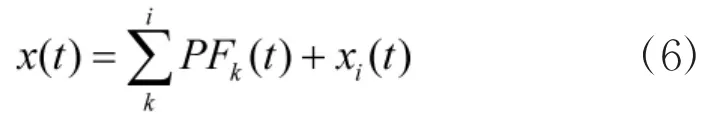
1.3 频域近似熵算法描述

随机信号进行LMD分解后的PF分量为依次从高频至低频序列，故用近似熵对PF分量进行量化，可实现以PF分量的复杂性作为目标的有用信息提取。

文献［14］中对信号频域近似熵算法计算过程如下：

①通过对离散信号序列进行傅里叶变换得到频谱分量：

②将变换的离散序列扩展为m维序列：

目前商船船间的数据链主要是依赖AIS技术，所提供的带宽仅为9.6 Kbit/s，另据目前研究进展报告，正在处于研发阶段的VDES理论带宽也仅为370.2 Kbit/s，这些难以为E-Navigation战略提供足够的技术支撑。而目前舰船识别数据链技术已经相对成熟，可为舰船间提供兆级以上带宽，作用距离可达到6 n mile以上，满足船间避碰操作对距离的要求，并可用于近距离船舶之间的信息交互。

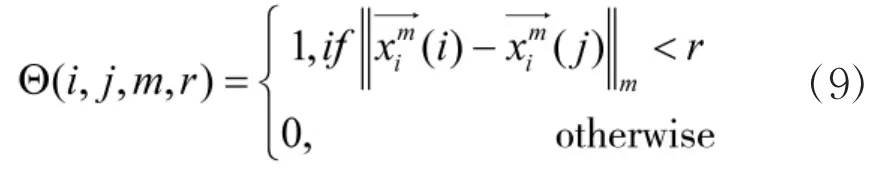
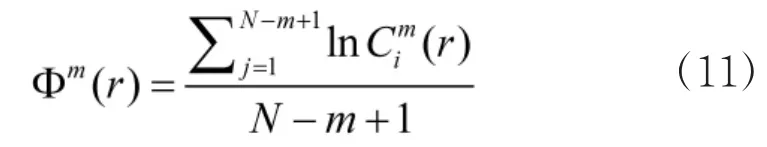
⑤定义频域近似熵计算过程为：

显然，通过对近似熵算法步骤的分析，可以得到频域近似熵值均与m，r，N的取值有关。Pincu建议其取值为m=2，r=0.1～0.2σ（σ是原始数据的标准偏差）。在文中，取参数m=2，r=0.15σ。

2 相关参数计算分析

2.1 LMD分量计算与选取

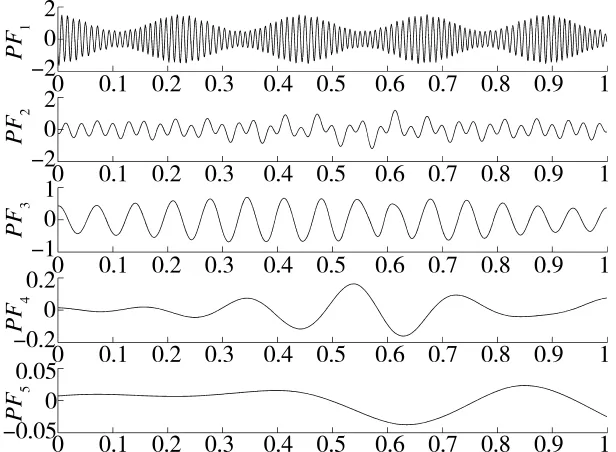
图2 调制信号LMD分解图

文献［13］指出，当LMD在机械故障诊断研究中运用时，PFi（t）分量存在虚假分量，而且选取分量过多，将会直接降低运算速度和检测效率。通过对LMD计算过程分析，由于将单调函数的出现作为运算的休止特征，显然每一个PFi（t）分量代表的源信号信息量在逐渐减少。文献［13］通过计算各PFi（t）分量互相关系数对数据进行相关性分析，运算得出前3个分量与对应原始信号的相关系数大于其余分量，前3个分量最能反映原始信号的特征。这与之前的分析相一致，故而在此选取前3个PFi（t）分量进行累加重构，得到一个新的，使分量在剔除干扰因素外，具备更为明显的信号高频信息，使提取的频域信息局部达到最优。同理，在其他条件不变的前提下，改变调制信号的信噪比，依次提取信号的PFj（t），作为近似熵计算的数据源。

2.2 LMD近似熵仿真计算分析

文献［12-13］中，将PFj（t）分量作为时间序列进行近似熵的计算用来对机械故障进行检测，结合信号频域近似熵算法，在本节中对不同信噪比条件下选取的PFj（t）通过式（2）进行傅里叶变换得到PFj（ω），并对LMD频域分量进行近似熵的计算，并在相同条件下按照文献［14］中所提方法直接计算离散信号频域近似熵，将两者作对比得到图3。

图3 不同信噪比条件下2ASK信号与噪声近似熵分布

图3给出的是当-30 dB≤SNR≤0 dB时，主用户信号的噪声、LMD和频域近似熵分布图。在信噪比的每个取值时，分别对200种不同的独立样本进行熵值计算，通过对这200个熵值取均值熵得到最终的结果。由图中可以看出，在-10 dB≤SNR≤0 dB范围内时，经过LMD提取的频域近似熵相较于直接计算的频域近似熵在数值差分明显，对调制信号更加敏感。因此，初步判断在低信噪比条件下，LMD近似熵相比于频域近似熵能更好地用于调制信号的感知。

3 性能仿真与分析

对于调制信号而言，通常研究的是信号的时域以及频域特性，本节通过对比不同噪声不确定度条件下LMD频域近似熵算法和现有的频域近似熵算法检测性能，以及不同信号样本长度下LMD近似熵和频域近似熵的接收机工作特性曲线 ROC（Receiver Operation Characteristic Curves）分布比较两者在频谱感知上的性能指标差异。

在实际的信号传输过程中信道中的噪声存在着不确定性，因此，通过研究不确定性噪声对检测器性能的影响，进一步判断LMD近似熵和频域近似熵在频谱感知上的性能差异。假设所估计的噪声不确定度模型为［15］，其中表示噪声功率的估计值，σ2为真实的噪声功率，α表示噪声不确定度（α＞1），将 α转化为 dB形式表示为β=101gα，选取2ASK信号作为仿真的实验主用户信号，图4所示为噪声不确定度为β=0 dB，0.5 dB，1 dB时2ASK信号LMD近似熵和频域近似熵的频谱感知算法性能对比图。其余条件不变，样本长度固定为N=8 000，虚警概率固定为PFA=0.1，确定不同噪声不确定度条件下算法的检测性能PD。

图4 不同噪声不确定度条件下两种方法检测性能对比图

分析图中数据可得：当信号样本长度以及虚警概率一定时，两种方法检测概率PD都随着信噪比的增加而变大，但显然LMD近似熵算法的检测性能都明显优于频域近似熵算法。例如，噪声不确定度为0 dB时，当信噪比SNR大于-5 dB时，频域近似熵方法的检测概率PD大于0.9。而相同条件下，LMD近似熵算法在信噪比SNR大于-22 dB时可达到同等的检测性能，约有17 dB的改进，说明本文算法实现有效频谱感知的信噪比门限低于频域近似熵检测方法，LMD频域近似熵对低信噪比信号更加敏感，这也将直接减少检测时间提升检测效率。同时，文献［6］对香农熵频谱感知检测性能也进行了研究，其在相同条件下检测概率PD大于0.9时，信噪比SNR必须大于-7 dB，显然文中LMD近似熵算法的检测性能有了大幅度提升。

在对式（7）～式（12）的分析中，看到算法信号样本长度也会对算法本身产生影响，因此，选择对样本长度不同，LMD近似熵和频域近似熵检测性能的变化进行研究，进一步判断两者在频谱感知上的性能差异。实验中，设定噪声不确定度为β=0 dB，信噪比SNR=-24 dB，并保持一定，分别比较样本长度N=9 600，8 000，6 400，4 800条件下的LMD近似熵感知算法与N=8 000频域近似熵算法的ROC曲线性能差异。

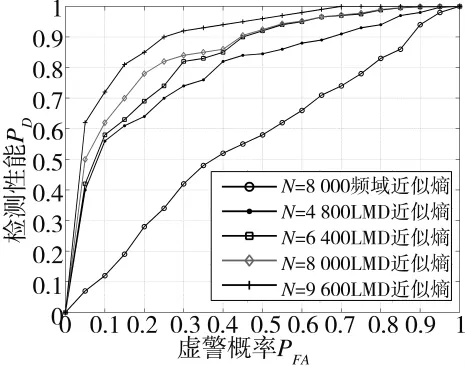
图5 不同样本长度下算法的ROC性能比较

由图5可见，相同信噪比条件下，样本长度越大，近似熵算法检测性能越好。而同条件下，基于LMD近似熵的感知算法检测性能远优于普通频域算法，这在一定程度上说明基于LMD频域近似熵的感知算法检测性能对信号长度的依赖性较低，算法具有更强的韧性，而且对调制序列信号的敏感性更高。

图6 本文算法下不同调制信号的检测性能分布图

图6反映的是不同调制方式对LMD近似熵感知算法的影响图示。仿真中调制信号样式分别为2ASK、BPSK、QPSK、2FSK，噪声不确定度设定为β=0 dB，虚警概率值PFA=0.1，其他参数与图4相同。由图6可得，在低信噪比条件下，不同调制方式信号在LMD近似熵感知算法检测性能上有所差异，其中2FSK性能最优，当信噪比大于-17 dB时，4种调制信号均能实现100%的检测概率，造成这种性能差异的原因在于近似熵值的分布不同。

4 结论

本文提出了一种基于LMD频域近似熵的频谱感知算法，通过计算信号在LMD频域上的近似熵值进行统计分析，可以实现低信噪比条件下的调制信号检测感知。仿真结果表明，本文所提算法在无信号先验信息、低信噪比条件下，能实现对主用户调制信号的有效感知，且其检测性能优于相同条件下的普通的频域近似熵感知算法和香农熵感知算法。

［1］陈雷，李永成，王英泓，等.认知无线电的频谱感知算法研究［J］.通信技术，2013，47（9）：38-41.

［2］López-Benítez M，CASADEVALL F.Improved energy detection spec-trum sensing for cognitive radio［J］.Communications，IET，2012，6（8）：785-796.

［3］江金龙，查代奉，梁宁利.脉冲噪声环境下的韧性匹配滤波检测方法［J］.计算机工程，2010，36（14）：256-258.

［4］朱景晖，吴智勇，盛国芳，等.基于循环平稳特征检测的认知无线电［J］.广播电视信息，2011，18（5）：68-70.

［5］ZHANG Y L，ZHANG Q Y，MELODIA T.A frequency-domain entropy-based detector for robust spectrum sensing in cognitive radio networks［J］.Communications Letters.IEEE，2010，14：533-535.

［6］朱永建.基于信息熵的频谱感知方法［J］.舰船电子工程，2012，32（10）：137-139.

［7］SABAT S L，SRINU S，RAVEENFDRANADH A，et al. Spectrum sensing based on entropy estimation using cyclostation Systems and Networks［C］//2012 Fourth International Conference on，Bangalore，2012：1-6.

［8］陈小军.基于熵测度理论的高效频谱利用关键技术研究［D］.西安：西安电子科技大学，2011.

［9］任建文，张猛.近似熵在谐振接地系统故障选线中的应用［J］.电测与仪表，2015，43（12）：18-22.

［10］张超，陈建军.基于LMD近似熵和支持向量机的轴承故障诊断［J］.机械科学与技术，2012，31（9）：1539-1542.

［11］YENTES J M，HUNT N，SCHMID K K，et al.The appropriate use of approximate entropy and sample entropy with short data sets.［J］.Annals of Biomedical Engineering，2013，41（2）：349-365.

［12］袁忠，黄频波，耿文霞.基于近似熵谱的碳纤维复合材料层压板拉伸损伤声发射分析［J］.宇航材料工艺，2014，44（4）：73-77.

［13］张淑清，孙国秀，李亮，等.基于LMD近似熵和FCM聚类的机械故障诊断研究［J］.仪器仪表学报，2013，34（3）：714-720.

［14］朱万经.无线电入侵检测分类系统关键技术研究［D］.成都：电子科技大学，2012.

［15］López-Benítez M，CASADEVALL F.Signal Uncertainty in SpectrumSensing for Cognitive Radio［J］.Communications，IEEE Transactions on，2013，61（4）：1231-1241.

LMD Frequency Domain Approximate Entropy-based Spectrum Sensing Algorithm

ZENG Xu，MU Xiao-dong，WANG Shu-yang，ZHAO Dian
（Rocket Force University of Engineering，Xi’an 710025，China）

The existing spectrum sensing methods process two shortcomings，such as poor antinoise performance and detection performance under the condition of low Signal-to-Noise Radio（SNR）simulation，a LMD frequency spectrum sensing algorithm of approximate entropy is proposed to overcome these problems.Firsty，The algorithm which selects three PF components added up to extract the optimal local Frequency and envelope feature information，can further eliminate the influence of the noise uncertainty.Secondly，The algorithm calculates the approximate entropy of the cumulative component after it is Fourier transformed to promote the algorithm’s sniffing in frequency domain information and improve the performance of detection.The Monte Carlo simulation results show that compared with time domain approximate entropy algorithm，the detection performance of 2ASK signal has been improved about 17 dB，under the noise power uncertainty of 0 db，sampling numbers of 8 000. At the same time，the detection probability can achieve of 100%when the SNR is higher than-19 dB.

frequency domain approximate entropy，spectrum sensing，noise uncertainty

TN914

A

1002-0640（2017）05-0047-05

2016-03-09

2016-05-18

国家“863”计划重点基金资助项目（2011701AA221）

曾 旭（1992- ），男，湖北随州人，硕士研究生。研究方向：信息与通信工程技术。