三角形“心”问题的向量解法

江苏省灌云高级中学(222200)

张永楼●

三角形“心”问题的向量解法

江苏省灌云高级中学(222200)

张永楼●

向量是代数与几何的一个完美结合.三角形的四个“心”即外心、内心、重心和垂心，是三角形问题中经常考查的一个知识点，也是较容易被混淆的.将三角形中的边与角的关系转化为向量运算,将会使问题变得更简单易解,本文将研究如何利用向量方法来解决三角形的“心”问题.

一、向量与三角形的“垂心”

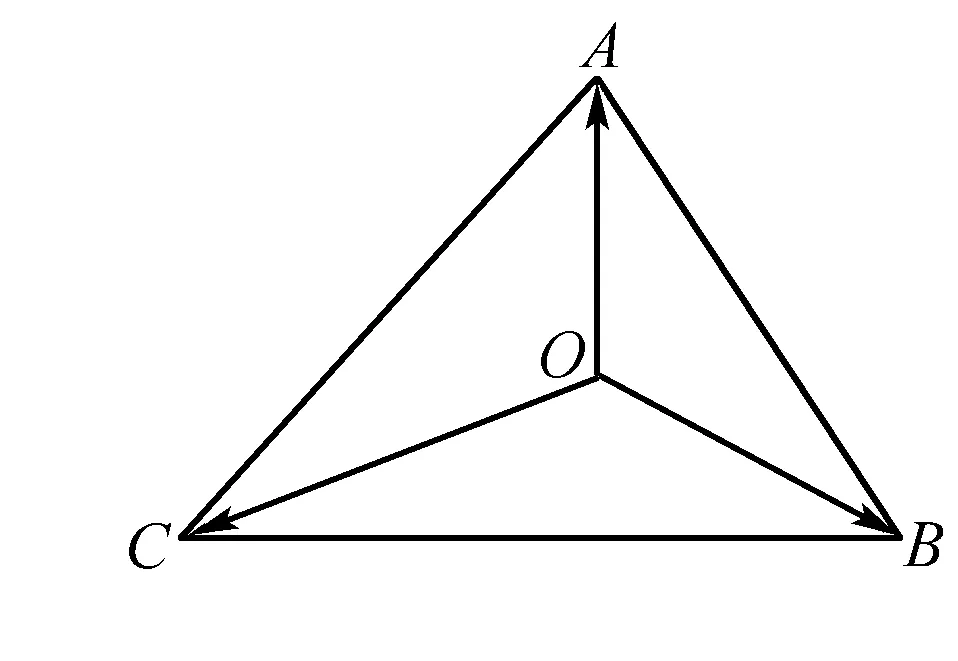
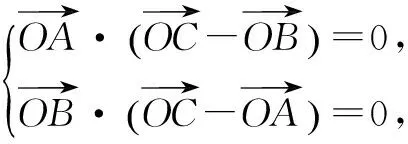
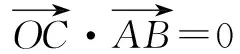
评注 在几何问题中,线线垂直可以转化为向量数量积等于零，反之，向量数量积等于零也可以转化为线线垂直.

二、向量与三角形的“外心”

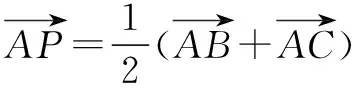
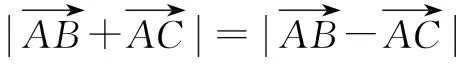
评注 向量平方等于向量模的平方，在解题中可以通过平方将向量的模转化为向量的运算来解答.

三、向量与三角形的“重心”

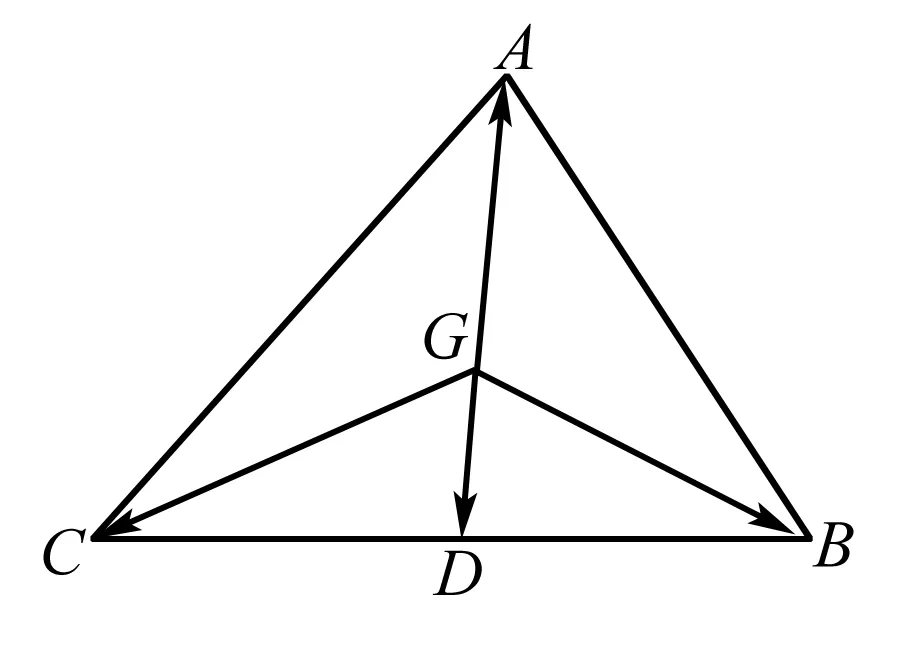
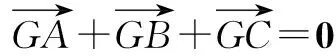
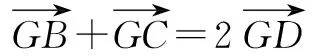
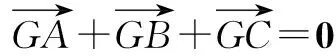
所以A,D,G三点共线，所以,点G在BC边的中线上.

同理,点G也在边AB,AC的中线上.

所以点G是△ABC的重心.

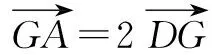
四、向量与三角形的“内心”

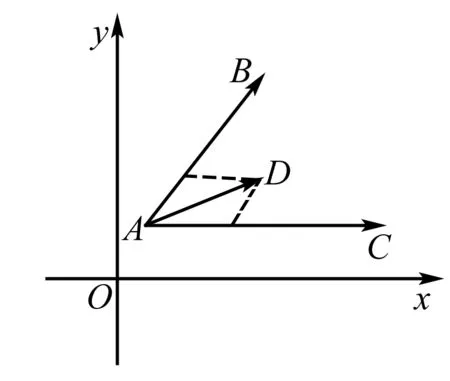
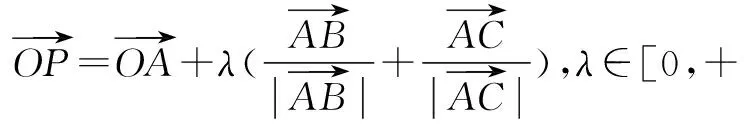
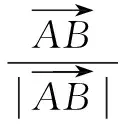
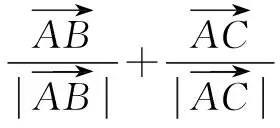
又因为λ∈[0,+),所以向量)与向量为共线向量,且方向相同.

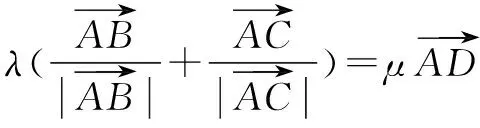
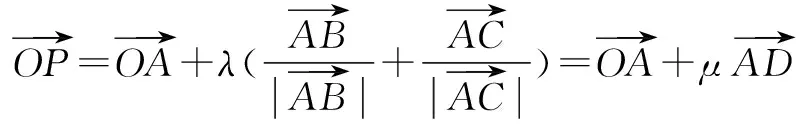
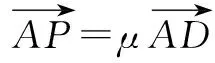
所以点P在AD上移动.即P点的轨迹一定通过△ABC的内心.

G632

B

1008-0333(2017)01-0038-01