析命题趋势 把复数之脉

云南省绥江县第一中学(657700)

余永波●

析命题趋势 把复数之脉

云南省绥江县第一中学(657700)

余永波●

纵观近几年高考试题容易发现,高考对复数的能力要求层次相对较低,主要以选择题、填空题的形式出现,考查复数的概念、四则运算、几何意义、复数相等以及与其他知识交汇,题目难度为容易题,但是考查的频率较高.

考点1:复数的有关概念

例1 设m∈R,m2+m-2+(m2-1)i是纯虚数,其中i是虚数单位,则m=____.

命题立意 本题考查纯虚数的概念.对于复数z=a+bi(a,b∈R),当b=0时,z是实数a；当b≠0时,z是虚数；当a=0且b≠0时,z是纯虚数bi.

例2 若复数z满足(3-4i)z=|4+3i|,则z的虚部为( ).

命题立意 本题考查复数的除法运算、模的运算以及虚部的概念.注意实部、虚部均包含其前面的正负号,特别是虚部为i前面的系数,而不包含虚数单位i.

A.-3 B.-1 C.1 D.3

考点2:复数相等的条件

例3 已知a,b∈R,i是虚数单位.若(a+i)(1+i)=bi,则a+bi=____.

解析 由(a+i)(1+i)=bi得a-1+(a+1)i=bi,即a-1=0,a+1=b,解得a=1,b=2,故a+bi=1+2i.

命题立意 本题考查复数的乘法运算以及复数相等的充要条件.a+bi=c+di⟺a=c且b=d,注意前提条件a，c，b，d∈R.

变式练习2 若i(x+yi)=3+4i,x,y∈R,则复数x+yi的模是( ).

A.2 B.3 C.4 D.5

考点3:复数的几何意义

命题立意 本题考查复数的四则运算以及复数的模的几何意义.

例5 若复数z满足iz=2+4i,则在复平面内,z对应的点的坐标是( ).

A.(2,4) B.(2,-4) C.(4,-2) D.(4,-2)

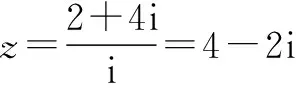
命题立意 本题考查复数的四则运算以及复数与复平面内对应点的几何意义.

变式练习3 设z=(2-i)2(i为虚数单位),则复数z的模为____.

变式练习4 i为虚数单位,设复数z1,z2在复平面内对应的点关于原点对称,若z1=2-3i,则z2=____.

考点4:共轭复数

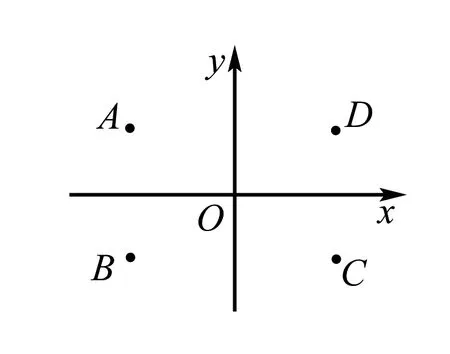
例6 如图,在复平面内,点A表示复数z,则图中表示z的共轭复数的点是 ( ).

A.AB.BC.CD.D

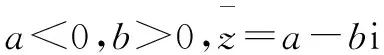
命题立意 本题考查复数与复平面内对应点的几何意义以及共轭复数的概念.

A.第一象限B.第二象限

C.第三象限D.第四象限

考点5:复数的四则运算

例7 设复数z满足(1-i)z=2i,则z=( ).

A.-1+iB.-1-iC.1+iD.1-i

命题立意 本题考查复数的四则运算,是复数考查的一大热点,其中以复数的除法最热. 复数的除法运算包含共轭复数、复数的乘法、实虚部整理的问题,因此受命题者青睐,同学们复习时一定要注意.熟记下列结论,可以快速解题,i2=-1,i4n=1,i4n+1=i(n∈N),(1+i)2=2i,(1-i)2=-2i等.

变式练习6 已知i是虚数单位,则(-1+i)(2-i)=( ).

A.-3+i B.-1+3i C.-3+3i D.-1+i

考点6:复数与其他知识综合

例8 已知集合M={1,2,zi},其中i为虚数单位,N={3,4},M∩N={4},则复数z=( ).

A.-2i B.2i C.-4i D.4i

命题立意 本题考查复数的简单运算、集合的基本运算以及元素与集合的关系,同时考查学生的转化化归能力.

答案:1.D；2.D；3.5；4.-2+3i；5.D；6.B

G632

B

1008-0333(2017)01-0025-01