参与方地位不平等条件下PPP项目超额收益分配研究

李 祎,王保乾

(河海大学商学院,江苏 南京 211100)

参与方地位不平等条件下PPP项目超额收益分配研究

李 祎,王保乾

(河海大学商学院,江苏 南京 211100)

PPP项目中政府部门通过最低收益担保为私人部门承担了大部分收益风险,因此公共部门在超额收益分配中占有强势地位。在考虑公私双方谈判地位不平等的基础上,构建PPP项目超额收益分配讨价还价模型,模拟真实的PPP超额收益谈判过程,为合理有效地分配PPP项目超额收益提供科学的决策依据,并通过模型结果分析得出影响PPP超额收益分配的关键因素。

PPP项目;超额收益分配;讨价还价;地位不对称

PPP项目的长期性、唯一性以及不完备契约性等特点使公私双方均面临着较常规项目更大的风险,同时PPP项目具有公共产品的性质,其定价以及收费机制难以完善,使其回报存在极大的不确定性[1]。巨大风险与收益不确定性严重影响投资者投资基础设施建设的积极性,因此在项目风险不能识别和控制的条件下,公共部门提供的最低收益担保将成为投资者介入基础设施的唯一的风险控制方法[2]。最低担保是指当投资者实际利润与担保量存在差值时,公共部门将对其进行相应补偿,因此它是投资者受益的直接保障[3]。最低收益担保针对的是PPP水利项目收益不佳时的情况,但是如果PPP项目建设运行良好,投资者极有可能会为获得垄断利润而提高项目的收费价格,进而损害公共利益[4]。因此,与最低收益担保相对应,公共部门还必须设置项目的收益上限,用以避免投资者通过自然垄断获得垄断利益。为了避免投资者为获得超额利润而侵害公共利益,当其收益高于公共部门设定的收益水平时,超额的收益部分应在公共部门和投资者之间进行分配[5]。超额收益的分配过程实则是公私双方的博弈过程,公共部门通过最低收益担保来降低投资者的收益风险,因此其在超额收益分配过程中处于“更高”的主动地位,因此其在超额收益的谈判过程中处于强势地位[5],但是若投资者不满于分配结果将会导致双方合作关系的破裂。因此,在PPP项目超额收益分配时如何在不忽视公私双方谈判地位不对称的条件下实现超额收益的最优分配,是一个亟待解决的问题。

1 文献综述

现阶段国内外对于PPP项目超额收益分配的研究主要集中在收益上限确定和超额收益分配两个方面。基于期权定价理论,Ashuri等[4]构建了根据最小收入保证(MRG)和收入上限(RCP)评估项目价值的数值模型,并通过对比得出考虑期权的项目净现值将会影响政府和私人资本的决策。Cheah等[6]以马来西亚—新加坡第二大桥项目为对象进行研究,并指出如果PPP超额收益发生时需降低收费标准、增加纳税,或者投资者将一部分超额收益交由政府。郭健等[7-8]基于实物期权理论,构建政府双边收入保证模型,运用期权定价模型确定出收入的上、下限。赵立力等[9]对PPP交通项目收入调节基金上下限设置的决策机制进行了研究,在此过程中对高速公路PPP交通项目的投资回报以及社会效益等因素进行了充分考虑。就目前而言,国内外学者对于PPP项目超额收益分配方面的研究相对较少,具有代表性的研究有:Kokkaew等[10]在对智利PPP交通项目的研究中将超额收入看作一种看涨期权,建立超额收益分配期权模型,并在假设政府和投资者商定平分超额收入的条件下进行求解。Vassallo[11]提出应当设置合理的投资回报率用以避免投资者获得超额收益,超出收益上限的收益部分应当按照一定的比例在公私之间分配,但是对于比例的确定方法却没有给出。郭健等[7]认为公共部门应该收纳所有超额收益,而这些超额收益可以用于车流量较低年份对投资者的补偿。

现阶段的PPP项目超额收益方面的研究大多数认为应将超额收益全部划分给政府部门,这种分配方式势必会导致私人部门的极度不满,引起合作双方的关系恶化;只有极少数学者提出应在公私双方之间进行合理分配,但是鲜有给出合理的分配比例和方法,且多基于双方地位对称的角度进行探讨,有悖于现实情况。因此,笔者从超额收益分配双方地位不平等的角度对PPP项目超额收益分配的实际谈判过程进行模拟，并在信息对称的条件下给出最优的超额收益分配比例,有效地避免双方合作破裂,提高双方合作效率。

2 模型构建

2.1 模型基本假设

假设一:公私部门均为以收益目标最大化的理性人,都期望避免谈判破裂;

假设二:对于PPP项目超额收益,公共部门占有的比例为θi(0<θi<1),而私人部门占有的比例为βi(βi=1-θi),即双方对θi展开讨价还价;

假设三:因为政府部门通过最低收益担保为私人部门承担一定的收益风险,所以它在超额收益的分配过程中占有主动地位,谈判中先出价。

2.2 模型参数的讨论

2.2.1 超额收益贴现率

超额收益贴现率σ(0<σ<1) 是本模型一个主要的参数,任何谈判均需要消耗一定的时间成本,这也就造成了公私双方在不同的时间阶段所获的超额收益有着不同的效用,谈判时间越长则双方获得超额收益的效用就会越小。私人部门与政府部门在谈判过程中均会承担一定的时间压力,无论是工期的延误,还是机械设备的保存,甚至是机会成本,对谈判者而言均是巨大的损失。如果PPP项目控制权谈判的周期较长,那么时间压力越大的参与者所获得的阶段收益折现到首期都是较低的。政府部门与私人投资者在实际的PPP项目所处的地位并不对称,政府部门是项目的发起者和最后拥有者,因此其无论是在谈判的信息资源的获取上还是谈判能力上都占据优势,即0<σG<σS<1。

2.2.2 地位的非对称性及程度

在超额收益分配的谈判过程中,政府部门在两方面占据优势:一方面,政府部门是PPP项目的发起者以及特许经营期之后的最终拥有者,其在PPP项目中扮演着“委托人”的角色,而项目私人投资者是项目的实施和管理者,其在PPP项目中扮演着“代理人”角色,因此政府部门在资源和信息的获取上占据更大的优势[12];另一方面，政府部门在PPP项目中通过最低收益担保在一定程度上降低了私人部门的投资风险[5],因而其在整个谈判过程之中具有主动地位。综上可知,公私双方在PPP超额收益分配过程中具有地位非对称性。超额收益分配过程中,具有强势地位的参与方会利用自身的强势地位强行占有额外的超额收益。在实际的PPP项目中,政府部门无疑占据超额收益谈判的主导地位,因此其势必利用自身地位优势占据额外的超额收益,本文用δi表示政府部门占有的额外超额收益比例,比例越高意味着公私双方所处地位非对称性就越强[12-13]。因为政府部门每一回合强占的超额收益比例不会大于私人部门所占有的比例,因此,0<δi<βi。

2.3 模型的建立

本文从公私双方都期望超额收益的角度,在考虑谈判双方地位不对称的基础上构建PPP项目超额收益分配的讨价还价模型。因此,讨价还价博弈模型如下:

第一回合:政府部门占有主动地位,率先提出自己占有θ1比例的超额收益,除此之外,其还会利用公私双方谈判地位的非对称性强占比例为δ1的超额收益,即私人部门实际获得超额收益比名义超额收益比例要少δ1,则此时政府部门G1与私人部门S1获得的超额收益比例分别为:

G1=θ1+δ1

(1)

S1=1-θ1-δ1

(2)

式中：G1与S1分别为在第一回合中公私双方获得的实际超额收益比例。假如投资者不满于第一回合的分配比例,则超额收益分配博弈将会进入下一轮。

第二回合:私人部门提出希望分配给政府部门比例为θ2超额收益,自己占有比例为1-θ2的超额收益,但是由于讨价还价过程中,合作双方均会存在损耗,无论是时间过程造成的工期拖延,机械设备折旧,还是机会成本的累积都会对双方造成不良影响,因此随着谈判进入第二轮,公私双方获得的真实超额收益效用也会相应发生损耗。同时,政府部门会利用自身的强势地位强占私人部门一定比例的超额收益,设比例为δ2,则公私双方在第二回合获得超额收益比例分别为

G2=σG(θ2+δ2)

(3)

S2=σS(1-θ2-δ2)

(4)

第三回合:政府部门提出自己占有的超额收益比例为θ3,与前两轮的情况相似,政府部门依旧会利用自身强势的地位占有比例为δ3的额外超收益,因此第三轮的谈判中,公私双方获得的超额收益比例为

(5)

(6)

如此往复,直至一方接受另一方的提议,谈判终止。

2.4 模型的求解

根据Shaked等[14]和Sutton[15]的结论:对于无限阶段的博弈,第一阶段与第三阶段是完全相等的。因此笔者用逆向归纳法求解三阶段的讨价还价博弈,先从第三阶段讨论双方的序列理性策略。

G2=G3

(7)

(8)

θ2=σG(θ3+δ3)-δ2

(9)

此时,私人部门获得的超额收益分配比例为

S2=σS(1-σG(θ3+δ3))

(10)

然后我走在了街上，就这样我要去看望我的这两个朋友，我在五岁的时候就认识了其中的一个，七岁的时候认识了另一个，他们两个人都比我大上四岁，三年前他们结婚的时候，我送给他们一条毛毯，在春天和秋天的时候，他们就是盖着我送的毛毯睡觉，所以他们在睡觉之前有时候会突然想起我来，他们会说：“快有一个月没有见到谁谁谁了……”

S2-S3=σS((σG-σS)(θ3+δ3)+(1-σS))

(11)

又因为1>σG>σS>0, 1>θ>0,1-θ>δ>0,则S2>S3,所以在第二轮的谈判过程中,公私双方均不希望将谈判拖入第三回合。

那么在第一回合中,政府部门同样会遇到相同的问题,因为政府部门如果提出占有θ1比例的超额收益,那么在第二回合中私人部门就会提出将收益比例定为θ2,则由公式(3)和(4)可知,公私双方在第二轮中获得超额收益比例分别为G2=σG(θ2+δ2)和S2=σS(1-θ2-δ2)。同第二轮谈判过程相似,如果政府部门在第一轮中的提议不能使私人部门获得的收益大于下一轮,那么谈判就会破裂,因此政府部门在第一回合提出的方案应当不仅使得自身收益最大化,而且还应当让私人部门接受,则政府部门的最优策略是:

S1=S2

(12)

将公式(2)和公式(10)带入公式(12)得:

θ1=1-σS-δ1+σSσG(θ3+δ3)

(13)

由Shaked[14]和Sutton[15]的结论可知,讨价还价的最小份额不随着谈判回合的变化而变动,因此有:

θ1=θ3=θ

θ=1-σS-δ1+σSσG(θ+δ3)

(14)

为了简便起见,本文进一步假设,δi=δ,则有:

θ=1-σS-δ+σSσG(θ+δ)

(15)

整理可得到公私部门在无限期讨价还价博弈模型中所占有的超额收益比例子博弈精炼纳什均衡为

(16)

(17)

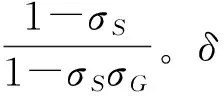
2.5 模型结果分析

3 结 论

政府部门在PPP项目中通过最低收益担保为私人部门承担了大部分风险,所以其在超额收益分配的谈判过程中占据主动地位;另一方面，由于政府部门处于PPP项目的发起者和最终拥有者的“委托人”角色,在获取资源与信息的能力上强于私人部门,基于此，笔者认为公私双方在超额收益分配过程地位具有非对称性。因此,在考虑公私双方地位不对称的基础上构建PPP项目超额收益分配的讨价还价模型,对超额收益分配过程进行更加真实的模拟,降低PPP项目超额收益分配过程的盲目与主观性,可为合理有效地分配超额收益提供科学的决策依据。与此同时,通过对模型结果的分析,笔者认为收益贴现率与地位不对称性程度是影响PPP项目超额收益分配结果的关键。此外,笔者认为政府部门实际占有的超额收益比例大于名义上应该占有的超额收益比例,因为其通过其地位非对称性占有了一部分私人部门的超额收益。私人部门只有掌握更多的项目资源与信息,且忽略谈判损耗,才有可能扭转在超额收益分配谈判过程的不利地位。

[ 1 ] 何涛,赵国杰. 基于随机合作博弈模型的PPP项目风险分担[J]. 系统工程, 2011(4): 88-92.

[ 2 ] 达霖·格里姆赛.PPP革命:公共服务中的政府和社会资本合作[M]. 北京: 中国人民大学出版社, 2016: 7-8.

[ 3 ] WIBOWO A, KOCHENDOERFER B. Selecting BOT/PPP infrastructure projects for government guarantee portfolio under conditions of budget and risk in the Indonesian context[J]. Journal of Construction Engineering & Management,2011, 137(7): 512-522.

[ 4 ] ASHURI B, KASHANI H, MOLENAAR K R, et al. Risk-neutral pricing approach for evaluating BOT highway projects with government minimum revenue guarantee options[J]. Journal of Construction Engineering & Management, 2013, 138(4): 545-557.

[ 5 ] WANG Y, LIU J. Evaluation of the excess revenue sharing ratio in PPP projects using principal-agent models[J]. International Journal of Project Management, 2015, 33(6): 1317-1324.

[ 6 ] CHEAH C Y J, LIU J. Valuing governmental support in infrastructure projects as real options using Monte Carlo simulation[J]. Construction Management & Economics,2006, 24(5): 545-554.

[ 7 ] 郭健. 公路基础设施PPP项目交通量风险分担策略研究[J]. 管理评论,2013, 25(7): 11-19.

[ 8 ] 郭健,尹洁林,林则夫. 期权视角下高速公路BOT项目风险分担策略研究[J]. 科技管理研究,2013, 33(13): 223-228.

[ 9 ] 赵立力,游琦. 高速公路BOT项目调节基金决策机制研究[J]. 管理工程学报, 2013, 27(3): 81-86.

[10] KOKKAEW N, CHIARA N. A modeling government revenue guarantees in privately built transportation projects: a risk-adjusted approach[J]. Transport, 2013, 28(2): 185-191.

[11] VASSALLO J M. Traffic risk mitigation in highway concession projects: the experience of Chile[J]. Journal of Transport Economics & Policy, 2006, 40(40): 359-381.

[12] 李林,刘志华,章昆昌. 参与方地位非对称条件下PPP项目风险分配的博弈模型[J]. 系统工程理论与实践, 2013, 33(8): 1940-1948.

[13] 马桑. PPP项目再谈判的博弈分析与模型构建[J]. 现代管理科学,2016(1): 40-42.

[14] SHAKED A, SUTTON J. Involuntary unemployment as a perfect equilibrium in a bargaining model[J]. Econometrica,1984, 52(6): 1351-1364.

[15] SUTTON J. Non-cooperative bargaining theory: an introduction[J]. Review of Economic Studies, 1986, 53(5): 709-724.

李祎(1992—),女,硕士研究生,从事区域经济和区域资源可持续发展研究。E-mail:allah_yiyi@163.com

王保乾(1964—),男,教授,博士,从事公共事业民营化研究。E-mail:307935855@qq.com

10.3880/j.issn.1003-9511.2017.03.004

F294

A

1003-9511(2017)03-0019-03

2017-01-17 编辑：陈玉国)