不确定型层次分析法在桥梁安全评估中的应用

赵 璐，程 龙

(河南理工大学 土木工程学院，河南 焦作 454000)

不确定型层次分析法在桥梁安全评估中的应用

赵 璐，程 龙

(河南理工大学 土木工程学院，河南 焦作 454000)

在桥梁安全评估中应用不确定层次分析法，建立层次分析模型，确立评估指标体系和计算权重。权重计算方法有4种，本文通过各种方法的比较，最终确定采用最优传递矩阵法。通过不确型层次分析法和最优传递矩阵法对斜拉桥进行安全评估，结果表明，此方法能够全面考虑影响桥梁安全性的多个主要因素，并且最优传递矩阵计算权重精度高，使桥梁评估结果更客观。

桥梁工程；安全性评估；不确定型层次分析法；最优传递矩阵

在桥梁安全性评估中，利用系统工程中的层次分析法将桥梁划分为层次分明的简单递阶层次模型，计算指标权重的基础数据来自区间数判断矩阵，现有多种计算方法，如区间数特征根法、区间数梯度特征向量法、区间数广义梯度特征向量法、区间数对数最小二乘法、区间数最小偏差法、区间数广义最小偏差法等。本文列举4种常用方法并比较其优缺点，在其中选取一种较合理的方法，对斜拉桥工程实例进行安全性评估。

1 不确定型层次分析法

层次分析法是将一个复杂问题作为1个系统，为方便处理，按影响较近或联系密切的因素划为一层，逐层划分，建立递阶层次模型。然后对各层因素(指标)进行两两重要程度比较赋值，由于认识事物的模糊性和不确定性，采用区间数代替确切数反映对事物认识的程度，构造区间数判断矩阵。 这就是不确定层次分析法的思想。其赋值比例标度如表1。2、4、6、8为Vi与Vj相比，重要程度处于相应两个数之间；Vi与Vj相比得判断Vij，则Vj与Vi相比得判断Vji=1/Vij。

表1 1～9标度尺

大型桥梁综合评估本身就是一个复杂的问题，通过AHP将影响桥梁状态的各因素条理化、层次化，建立递阶层次模型，然后通过加权综合的方法由底层指标得到上层指标的评估结果，逐级综合，最终得到整个桥梁的安全状态。桥梁安全评估步骤如下：

(1)建立桥梁评估的递阶层次模型。将对桥梁状态影响较近或联系密切的指标放为一层，建立多层次评估模型，指标体系即被确定。

(2)构造区间数判断矩阵，将本层各指标进行两两比较重要程度，采用表1进行赋值，如本层有n个指标，则形成的区间数判断矩阵形式如表2所示。

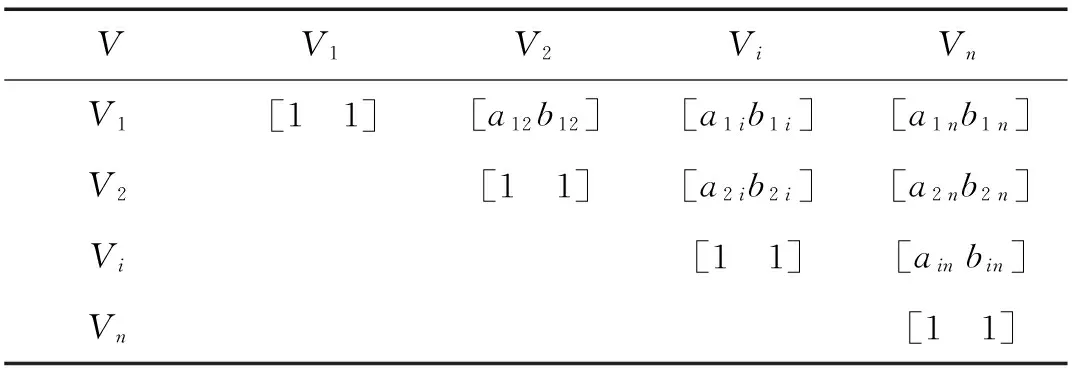
表2 区间数判断矩阵

(3)计算权重。由区间数判断矩阵计算各层指标相对权重。

(4)建立指标的隶属度函数。层次模型确立后，对桥梁整体和各指标划分等级标准。但各指标量纲不同，为统一量纲便于评估，对底层指标分别建立隶属度函数。本文采用梯形隶属度函数对各指标进行模糊化，形成模糊向量。

(5)模糊综合评估。将每层各指标计算所得模糊向量形成评估矩阵，与本层各指标权重相乘，即得到上层指标评估结果。逐层综合最终得到整个桥梁评估结果。其公式如下：

(1)

2 权重计算方法研究

2.1 4种方法间的比较

桥梁安全性评估中，权重计算方法较多，但权重计算基本数据信息均基于专家做出的判断矩阵，由此权重准确性除了受专家知识水平(专家水平)影响外，计算方法的合理性成为客观确定权重的主要因素。表3列出了4种常用方法的优缺点。最终本文拟采用最优传递矩阵法对斜拉桥进行安全性评估。

表3 4种指标权重计算方法的优缺点

2.2 最优传递矩阵法

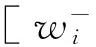
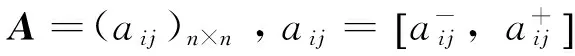
(3)将数字矩阵A=(aij)n×n采用B=lnA=(lnaij)n×n化为反对称矩阵，B为A的反对称矩阵[3]；

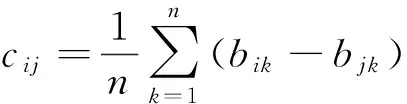
(5)将C化为一致性矩阵A*，A*=(ecij)n×n，最终按下式计算指标权重：

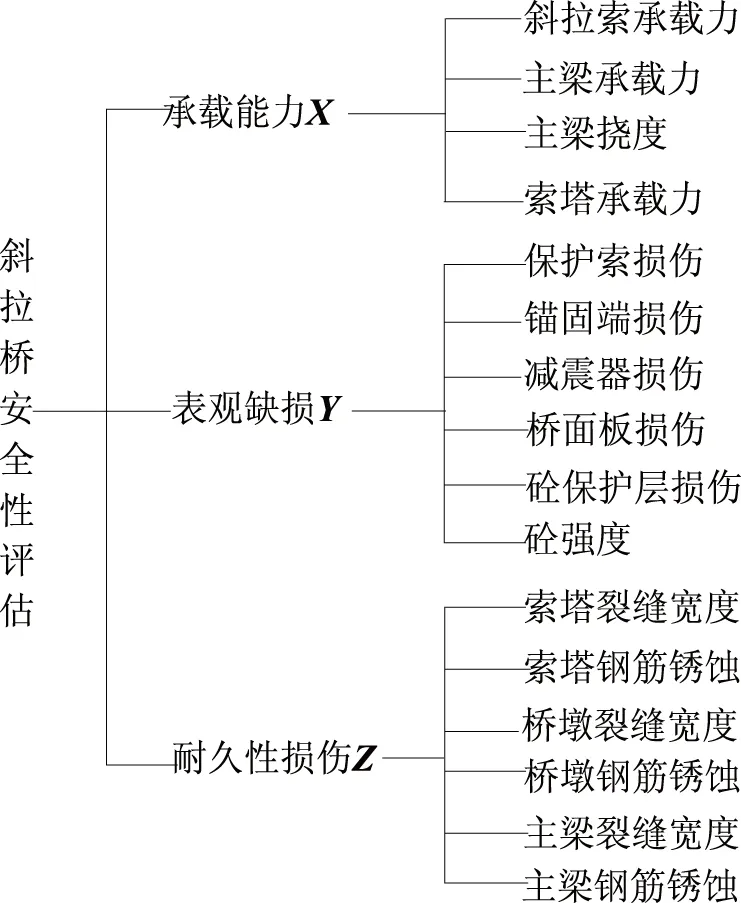
图1 斜拉桥递阶层次模型

(2)

3 工程实例分析

结构物的安全评估中，当指标体系确定以后，影响评估结果准确性的因素主要是权重的准确性。根据上述4种方法的优缺点对比，为提高桥梁安全评估准确性，采用最优传递矩阵法使桥梁评估更加合理可靠。

针对某预应力混凝土斜拉桥，递阶层次模型如图1所示。仅列专家对一级指标构造的判断矩阵如表4所示。

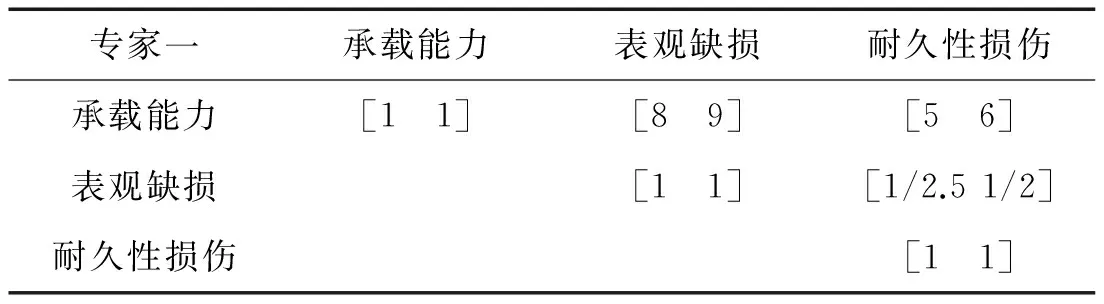
表4 两两判断矩阵调查表

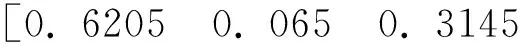
AX=[0.345 0.134 0.362 0.159]；

AY=[0.228 0.210 0.126 0.107 0.125 0.204]；

AZ=[0.167 0.167 0.166 0.166 0.167 0.167]。

本文将斜拉桥评估划为5级[7]，评语集为良好，较好，较差，坏，危险，计算出各因素隶属于评语集中各等级的程度，组成相应的评估矩阵分别为：

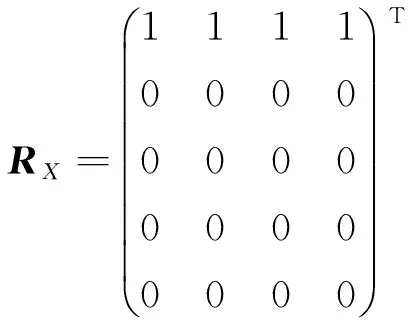
通过模糊变换，逐层递推到最高层得到斜拉桥安全评估结果为：

B=A×R=[0.936 8 0.063 2 0 0 0]。

最后得到整个斜拉桥总体评估结果为：根据隶属度临近法(0.936 8)，斜拉桥状态良好。

4 结 语

通过采用不确定型层次分析法对桥梁进行评估研究，并运用于斜拉桥的评估中，得出如下结论：

(1)将不确定型AHP运用于桥梁的评估中，能够较全面地考虑影响桥梁安全性和耐久性的主要因素，反映桥梁综合状态。通过建立完整合理的桥梁评估系统，可为桥梁维护管理提供理论依据，保证桥梁安全和延长桥梁使用寿命。

(2)通过对斜拉桥安全评估，运用不确定层次分析法建立斜拉桥梁的递阶层次模型和评估指标体系，确定指标权重并得到该桥梁的综合结果，证明此方法的科学性与实用性。

[1] 黄侨，任远，林阳子.大跨径桥梁综合评估中的不确定层次分析法[J].公路交通科技，2008,25(3)：79-83.

[2] 张彬，张佳.基于最优传递矩阵的层次分析法在桥梁震害评估中的应用[J].灾害学，2010,25(3)：32-36.

[3] 袁海庆，刘文龙，殷银章，等.不确定型层次分析法在桥梁综合评估中的应用研究[J].铁道运输与经济，2006,28(2)：82-85.

[4] 范剑锋，袁海庆，刘文龙，等.基于不确定型层次分析法的桥梁模糊综合评估[J].武汉理工大学学报，2005,27(4)：54-57.

[5] 范剑锋，袁海庆，钟珞.不确定层次分析下的桥梁评估最优指标权重确定[J].公路交通科技，2007,24(9)：65-68.

[6] 单德山,李乔，徐威.不确定层次分析法在砼桥梁性能评价中的应用[J].重庆交通学院学报(自然科学版)，2007,26(1)：19-22.

[7] 宗周红,朱三凡，夏樟华.大跨径连续刚构桥安全性评估的综合分析方法[J].铁道学报，2011,33(7)：110-117.

Application of Uncertain AHP on Bridge Evaluation based on Optimal Transfer Matrix

ZHAO Lu， CHENG Long

(Henan Polytechnic University, Jiaozuo 454000, China)

Analytic hierarchy model is set up in the process of uncertain AHP application to bridge engineering assessment. Evaluation index system and weight calculation are established. There are kinds of methods of weight calculation method. optimal transfer matrix method is used through the comparison of several methods. Safety assessment of cable-stayed bridge is done by the uncertain AHP and the optimal transfer matrix method. Results show that this method can fully consider the several main factors influencing the bridge safety and durability. calculating weight precision of optimal transfer matrix is so good that make the bridge evaluation results more objective.

bridge project；safety assessment；uncertain AHP；optimal transfer matrix

2017-02-20

赵璐(1990-)，男，河南安阳人，在读硕士研究生，主要从事地质灾害防治方面的研究.

10.3969/i.issn.1674-5403.2017.02.006

U447

A

1674-5403(2017)02-0020-04