一类理想化主动磁轴承不对中转子系统的动力学分析

杨 琼，黄萌佳

(兰州交通大学 数理学院，甘肃 兰州 730070)

一类理想化主动磁轴承不对中转子系统的动力学分析

杨 琼，黄萌佳

(兰州交通大学 数理学院，甘肃 兰州 730070)

研究了一个二自由度理想化主动磁轴承不对中转子系统的动力学模型，并分析了电磁力对转子线圈电流和位移的影响。通过线性正交轴刚度、阻尼系数及轴和定子之间的气隙，确定出主动磁轴承系统的参数。利用MATLAB软件进行数值模拟，分析了各参数对主动磁轴承不对中转子系统的动力学影响。

磁体；磁力；角误差 ；动力学常数

1 主动磁轴承不对中转子模型

主动磁轴承已经被广泛的应用到许多工业和研究领域。尤其对于旋转机械而言，其旋转零部件(主要是转子)的振动将直接影响到机器的效率、寿命和人身安全，据统计在所有旋转机械的故障中，大部分是由转子的不对中引起的，因此研究不对中的旋转机械是非常具有现实意义的。 一个有角度偏差的主动磁轴承不对中转子的理想化模型坐标图如图1所示。图1是以圆盘中心为坐标原点的。其中：α(t)+αi是不对中转子在(x,y)面上的角误差，β(t)是不对中转子在(x,z)面上的角误差。

图1 有角度偏差的主动磁轴承不对中转子的理想化模型坐标图

2 运动方程的建立

假设所有的磁体都是理想化的，即可以忽略磁漏、边缘的磁通量、各磁体之间的耦合效应.从文献[1]中可以得到电磁力Fj的表达式：

(1)

其中：μ0是导磁率，A是电磁体的横截面，N是绕磁线圈的数量，C0是定子和轴之间的气隙，I0是可以产生电磁场的偏置电流，Ij是j方向上的控制电流，δj是j方向上转子的位移，θ是重拨电磁的响应半角。

(2)

其中：i0是产生平衡转子重量控制电流的静态分量，kp和kd分别表示比例增益和微分增益，ij是控制电流的反馈分量，φj是电磁轴承的第一个磁极和第j个磁极所成的角，令电磁轴承的第一个磁极与x轴的夹角φ1，即φ1=0°。

不同磁极个数轴承的位移方程如下：

(3)

(4)

(5)

(6)

其中:Ω 是转子的角速度，L是转子的长度，L1是电机轴承的高度，L2是轴承和电机轴之间的距离，L3是轴承与轴承之间的距离，Ra是耦合半径，αi是角度偏差，R是圆盘半径。

(7)

将方程(3)、方程(4)、方程(5)、方程(6)分别代入式(2)、式(1)、式(7)中就可以得到水平方向和垂直方向的电磁力Fy和Fz。

2.1 主动磁轴承系统的非线性电磁力

(1)n=4即φ1=0°,φ2=90°时，

δ1=ycosφ1+zsinφ1,δ2=ycosφ2+zsinφ2,δ1′=y′cosφ1+z′sinφ1,

综合化简上述方程可得：

(8)

(9)

(2)n=6即φ1=0°,φ2=60°,φ3=90°时，

(10)

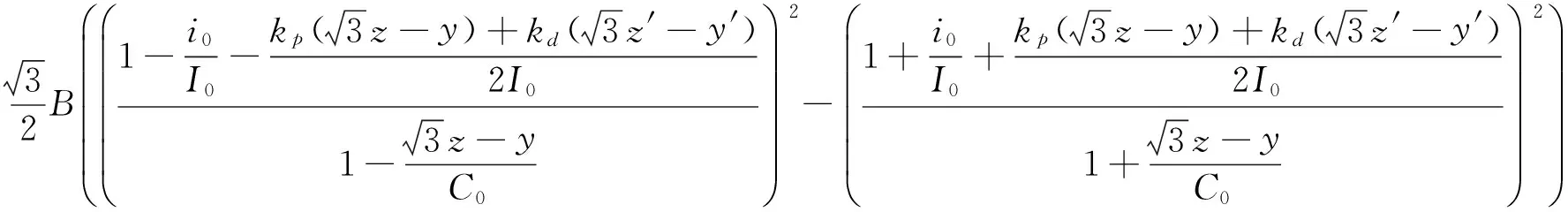
(11)

(3)同理，当n=8即φ1=0°,φ2=45°,φ3=90°,φ4=135°时， 可以计算出相应的Fy8和Fz8。

2.1.1 磁力的数值模拟

磁力随时间变化的响应图如图2所示。代表不同磁极在y方向和z方向的磁力。 通过对比可知，磁极个数越多磁力越大。 且y方向的磁力比z方向的磁力大。图(a)、(b)、(c)分别表示磁极个数为4、6、8时，y、z轴方向受到的磁力的大小。

图2 磁力随时间变化的响应图

2.2 主动磁轴承系统的动力学常数

在文献[3-4]中可以得到随位移和转速线性增加的刚度系数。在此不考虑阻尼系数的影响。刚度系数与位移有如下关系：

(12)

其中：(x0,y0)是静态平衡位置o0的坐标。

2.2.1 数值模拟

刚度随气隙变化的响应图如图3所示。 当气隙值较小时， 刚度的减小幅度变大，其中磁极个数越多， 气隙对刚度系数C0的影响越大。 图(a)、(b)分别为yz方向刚度随气隙的变化，当气隙增大，刚度系数大幅度下降。

图3 刚度-气隙变化响应图

2.3 不对中转子轴承系统

2.3.1 不对中转子方程建立

通过系统的动能：

(13)

(14)

为方便计算，令Cyy=Cyz=Czy=Czz=C，则系统的亏损能量为：

(15)

文献[3]依据拉格朗日公式、动能方程以及亏损方程可以得到不对中转子系统α(t)和β(t)的运动方程：

(16)

其中：M(t)是惯性矩阵，

(17)

m1=m(E2+R2cos2(Ωt))-I

(18)

m2=m3=mR2cos(Ωt)sin(Ωt)

(19)

m4=m(E2+R2sin2(Ωt))+I

(20)

C(t)是描述陀螺效应和阻尼效应的矩阵，

(21)

C1= -2mR2Ωcos(Ωt)sin(Ωt)+Cyy[(B2+D2)cos(αi)+2A2sin(αi)2-2Acos(αi)sin(αi)(B+D)]，

(22)

(23)

C3= -2mR2Ωsin(Ωt)2+B(Cyz+Czy)(Bcos(αi)-Asin(αi))+D(Cyz+Czy)(Dcos(αi)-Asin(αi)),

(24)

C4=mR2Ωsin(Ωt)cos(Ωt)+Czz(B2+D2),

(25)

(26)

K1=mREΩ2cos(Ωt)sin(αi)-mR2Ω2cos2(Ωt)cos(αi)+Kyy[A(B+D)(sin(αi)-

4cos(αi)sin(αi))+(B2+D2)(cos2(αi)-sin2(αi))+2A2(cos(αi)+sin2(αi)-cos2(αi))]，

(27)

(D2cos(αi)-ADsin(αi))]，

(28)

(D2cos(αi)-ADsin(αi))]+Cyz(BRΩsin(Ωt)sin(αi))+Cyz(DRΩsin(Ωt)sin(αi))，

(29)

K4=mREΩ2cos(Ωt)sin(αi)-mR2Ω2sin(Ωt)2-2Cyz[ARΩsin(Ωt)(1-cos(αi))]+

(30)

(31)

f1=mREΩ2cos(Ωt)(cos(αi)-1)-2R2Ω2cos(Ωt)2sin(αi)-Kyy[(B2+D2)sin(αi)cos(αi)+

A(B+D)(cos2(αi)-sin2(αi)-cos(αi)+2A2sin(αi)(1-cos(αi)))]-KyyRΩsin(Ωt)×

(1-cos(αi))(Bcos(αi)+Dcos(αi)-2Asin(αi))，

(32)

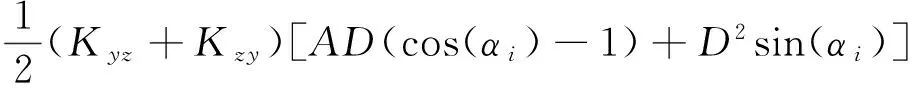
(33)

2.3.2 数值模拟

3 结 语

本文研究了不同参数对主动磁轴承不对中转子系统的影响。在轴承系统中，当转轴和定子之间的气隙增加时，系统的支护参数减小。并且当磁极个数不同时，角误差、气隙对第二个波峰的影响也不同。

图4 偏角-时间变化的响应图

[1] Zhang W,Yao M H,Zhan X P.Multi-pulse chaotic motions of a rotor-active magnetic bearing system with time-varying stiffness[J].Chaos Solitons Fractals,2006,27:175-86.

[2] Eissa M H,Hegazy U H,Amer Y A.Dynamic behavior of an AMB supported rotor subject to harmonic excitation[J].Appl Math Model,2008,32:1370-80.

[3] Bouaziz S,Attia H M, Maatar M,et al.Dynamic behaviour of hydrodynamic journal bearings in presence of rotor spatial angular misalignment[J].Mech Mach Theory,2009,44:1548-59.

[4] Bouaziz S,Attia H M,Maatar M,et al. Angular misalignment effect on hydrodynamic journal bearings dynamical behaviour[J].Int J Eng Simul,2007,8(1):3-10.

[5] Slim B,Najib B M,Mohamed M,et al.A theoretical model for analyzing the dynamic behavior of a misaligned rotor with active magnetic bearing[J].Mechatronics,2011,21:899-907.

[6] 黄文虎,武新华,焦映厚,等.非线性转子动力学研究综述[J].振动工程学报,2000,13(4):497-509.

[7] 李明.平行不对中转子系统的非线性动力学行为[J].机械强度,2005,27(5):580-585.

Idealized Dynamic Behavior Analysis of Misaligned Rotor with Active Magnetic Bearings

YANG Qiong, HUANG Mengjia

(Lanzhou Jiaotong University, Lanzhou 730070, China)

In the paper, a two-degrees of freedom ideal dynamic model of a misaligned rotor with active magnetic bearings was studied and the magnetic forces on the influence of the rotor, the basic current and the displacements of the rotor were also analyzed. Meanwhile, the dynamic parameters were modeled with linear direct cross axes stiffness, damping coefficients and the air gap between the stator and the shaft. Finally, the system of misaligned rotor parameters can be simulated with MATLAB to test the effects of misaligned rotor with active magnetic bearings.

magnetic; electromagnetic forces; misalignment defect; dynamic coefficients

2016-12-04

杨琼(1991-)，女，甘肃秦安人，在读硕士研究生，主要从事非线性动力学方面的研究.

10.3969/i.issn.1674-5403.2017.02.023

O322

A

1674-5403(2017)02-0088-06