归纳猜想型问题的解决方法

马国建

归纳猜想型问题的解决方法

马国建

英国物理学家牛顿说过:“没有大胆而放肆的猜想，就不可能有伟大的发现.”归纳猜想型问题在中考中越来越被命题者所注重.这类题要求根据题目中的图形或者数字分析归纳，直观地发现共同特征，或者发展变化的趋势，据此去预测估计它的规律或者其他相关结论，使带有猜想性质的推断尽可能与现实情况相吻合，必要时可以进行验证或者证明，依此体现出猜想的实际意义.

一、数字猜想型

通常给定一些数字、代数式、等式或者不等式，然后猜想其中蕴含的规律.一般解法是先写出数式的基本结构，然后通过横比（比较同一等式中不同部分的数量关系）或纵比（比较不同等式间相同位置的数量关系）找出各部分的特征，改写成要求的格式.

例1 按规律填数：

（1）-3、+6、-12、+24、 .

【分析】（1）经观察不难发现，后一个数是前一个数的-2倍，计算即可得解；

（2）经观察不难发现，分子是不断减小的连续的奇数，分母是3的指数次幂，且第奇数个是负数，第偶数个是正数，写出即可.

解：（1）∵-3、+6、-12、+24，

【点评】本题是对数字变化规律的考查，比较简单，题（2）要从分子、分母两个方面考虑数值的变化.

二、猜想数式规律：

例2 观察下列等式：

1+3=22，

1+3+5=32，

1+3+5+7=42，

1+3+5+7+9=52，

……

请将你发现的规律用仅含字母n（n为正整数）的等式表示出来：

【分析】经观察不难发现，从1开始的连续奇数的和等于奇数的个数的平方，根据此规律解答即可.故答案为：1+3+5+7+…+（2n-1）=n2.

【点评】本题是对数字变化规律的考查，观察出从1开始的连续奇数的和等于奇数的个数的平方是解题的关键.

三、图形排列规律型

根据一组相关图形的变化规律，从中总结通过图形的变化所反映的规律.其中，以图形为载体的数字规律最为常见.猜想这种规律，需要把图形中的有关数量关系列式表达出来，再对所列式进行对照，仿照猜想数式规律的方法得到最终结论.

例3 请用同样大小的正方形纸片按以下方式拼成大正方形.仔细观察寻找规律：

第1个图

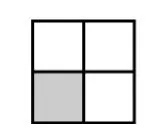
第2个图

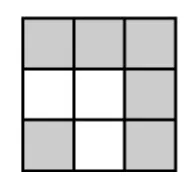
第3个图

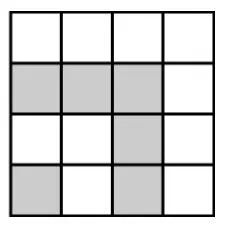
第4个图

第1个图形中有1个小正方形；

第2个图形比第1个图形多_____个小正方形；

第3个图形比第2个图形多_____个小正方形；

第4个图形比第3个图形多_____个小正方形.

（1）第10个图形比第9个图形多多少个小正方形？

（2）第100个图形比第99个图形多多少个小正方形？

（3）第n个图形比第（n-1）个图形多多少个小正方形？

（4）你还有什么发现？

【分析】根据已知图形得出第2个图形比第1个图形多4-1=3个小正方形，第3个图形比第2个图形多9-4=5个小正方形，第4个图形比第3个图形多16-9=7个小正方形，即可得出后面一个图形比前面一个图形多的小正方形个数是连续奇数，进而得出公式第n个图形比第（n-1）个图形多（2n-1）个小正方形.

解：（1）第10个图形比第9个图形多2× 10-1=19个小正方形；

（2）第100个图形比第99个图形多2× 100-1=199个小正方形；

（3）第n个图形比第（n-1）个图形多2n-1个小正方形；

（4）还可以看出后面一个图形正方形多的个数正好是前一个正方形一条边上的正方形个数的2倍加上1.

【点评】此题主要考查了图形的变化规律，利用已知图形得出相邻图形之间的个数变化规律是解题关键.

提炼 我可以发现第1个图形有1个小正方形.

由图形可以发现1+3+5+7+9+…+（2n-1）=______.（用含有n的代数式表示）

【解答】1+3+5+7+…+（2n-1）=n2.

四、坐标变化型

例4 如图，直线y=x+1分别与x轴、y轴相交于点A、B，以点A为圆心，AB长为半径画弧交x轴于点A1，再过点A1作x轴的垂线交直线于点B1，以点A为圆心，AB1长为半径画弧交x轴于点A2，……，按此做法进行下去，则点A8的坐标是（ ）.

A（.15，0） B（.16，0）

【分析】根据题意，利用勾股定理求出AA1，AA2，AA3的长，得到各点坐标，找到规律即可解答.

解：当x=0时，y=1，

当y=0时，x=-1，

可得A（-1，0），B（0，1），

AA1=AB=

同理，AA2=AB1=2，AA3=AB2=22，

A（3），

可得A（828-1，0），即A（815，0）.

【点评】本题考查了一次函数图像上点的坐标特征，熟练运用勾股定理是解题的关键.

（作者单位：江苏省常州市金坛区第五中学）