基于变形修正的反应位移法改进研究

宾 佳，景立平，李永强

（1. 湖南工业大学 土木工程学院，湖南 株洲 412007 ；2. 中国地震局工程力学研究所，黑龙江 哈尔滨 150080）

基于变形修正的反应位移法改进研究

宾 佳1，景立平2，李永强2

（1. 湖南工业大学 土木工程学院，湖南 株洲 412007 ；2. 中国地震局工程力学研究所，黑龙江 哈尔滨 150080）

对目前地下结构抗震分析中的土-结相互作用系数法和反应位移法进行了分析，结合二者的优点，提出了一种基于变形修正的改进反应位移法。改进反应位移法是在传统反应位移法的基础上，通过土-结相互作用系数法中的结构变形，对反应位移法中的结构变形进行修正，从而对结构内力进行调整，减小了传统反应位移法的误差。为验证改进方法的有效性，通过改变结构的截面尺寸、土体刚度和结构埋深，分别用传统反应位移法、改进反应位移法和动力时程分析方法进行对比计算。结果表明：改进反应位移法的计算结果要好于传统反应位移法；改进反应位移法只是整体地放大或缩小传统反应位移法的计算结果，并不能改变结构内力的分布形式；传统反应位移法仍存在较大的误差。

地下结构；抗震分析；反应位移法；土-结相互作用系数法

1 研究背景

自1995年日本阪神地震以来，国内外研究学者针对地下结构抗震分析开展了大量研究，并提出了多种地下结构抗震设计分析方法[1]。现有的地下结构抗震设计方法主要有3类：解析法[1]、拟静力方法[2-6]和动力时程方法[7-8]。其中，解析法的求解条件过于理想，与实际情况相差较大，该方法主要用于结构的初步设计；动力时程方法涉及人工边界的设置以及土体动力本构等问题，计算技术要求较高，难以在工程中广泛使用；而拟静力方法形式较为简单，物理意义明确，能够比较全面地考虑地下结构地震反应时的特点，是一种比较实用的计算方法。

已有拟静力抗震设计方法中，应用较多的有土-结相互作用系数法和反应位移法等。土-结相互作用系数法通过采用一个系数来考虑土体和结构相对刚度的不同。该方法通过解析解及数值解的形式给出了不同土-结相对刚度下自由场应变和结构应变之间的关系，通过该关系可由自由场应变求得结构应变。近年来，Wang J. N.[2]、J. Penzien[9]、J. H. Wood等[10]对土-结相互作用系数法做了大量研究，但由于该方法计算模型以及荷载施加方式等方面的不足，造成即使在结构变形与地震作用下结构的真实变形一致时，结构内力仍与真实内力相差较大，误差可达50%以上。反应位移法则是采用集中弹簧的形式来取代周围土体对结构的约束作用，而地震荷载的施加则是通过自由场的剪应力、相对位移和加速度换算而来的。近年来，立石章[3]、刘晶波等[11]、董正方等[12]、耿萍等[13]也分别从参数求解、理论推导以及方法适用性等方面，对反应位移法进行了大量的研究，取得了丰硕的成果，但是在弹簧系数取值、地震荷载施加等方面也存在较多问题。已有研究表明，反应位移法的误差可达30%。

本文在分析土-结相互作用系数法和反应位移法优缺点的基础上，综合两者的优点，提出了基于变形修正的反应位移法。并采用该改进反应位移法与传统反应位移法以及动力时程方法进行对比计算，以验证该改进方法的有效性。

2 土-结相互作用系数法

土-结相互作用系数法，是在自由场变形法的基础上，通过一个系数来考虑土体和结构相对刚度的不同。对于土-结相互作用系数，J. Penzien、T. Nishioka等、Wang J. N.等都提出了不同的计算方法，本文采用J. Penzien的计算方法[9]，如式（1）所示。

土-结相互作用系数法的计算模型如图1所示，其采用两铰支座对结构底部角点进行固定，地震荷载则是通过作用到结构顶点上的集中力F来施加。集中力F的大小取决于式（1）得到Δst的大小，从而可得到结构在地震作用下的内力。

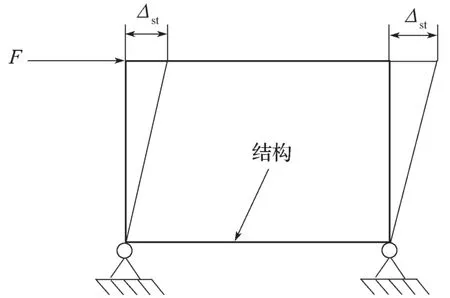
图1 土-结相互作用系数法计算模型Fig. 1 Calculation model of soil-structure interaction coef fi cient method

土-结相互作用系数法存在如下不足：

1）底部采用铰支座来固定结构，并不能很好地反应土体对结构的约束作用；

2）地震荷载只是采用简单的集中力的形式，并不能准确地反应实际地震作用下结构所受到的地震作用。

土-结相互作用系数法的优点为：该法能较为准确地通过土-结相互作用系数来由自由场的应变确定出结构的应变。

3 反应位移法

反应位移法最早由日本学者提出，现已应用到我国的地下结构抗震设计规范之中。反应位移法的计算模型如图2所示，它是以集中弹簧的形式来近似取代周围土体对结构的相互作用，结构采用梁单元模拟，通过土体等效弹簧与梁单元之间的连接来表现土与结构之间的相互作用。

同时，反应位移法中地震荷载的施加主要通过3个部分：土层变形、剪应力以及惯性力。

土层变形：通过在弹簧端部施加如式（2）所示的等效荷载来实现。

剪应力：顶面和底面剪应力，采用一维土层反应分析时对应位置的剪应力；而侧面剪应力，采用顶面和底面剪应力和的一半。

惯性力：采用结构对应自由土层位置处的加速度乘以结构的质量。

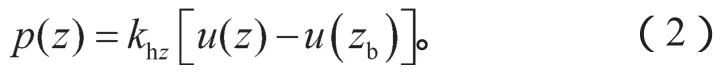
式中：p(z)表示深度z处因自由土层位移产生的力；u(z)表示深度z处自由土层地震反应位移；u(zb)表示结构底部深度zb处的自由土层地震反应位移；khz表示深度z处土体的水平向弹簧系数。

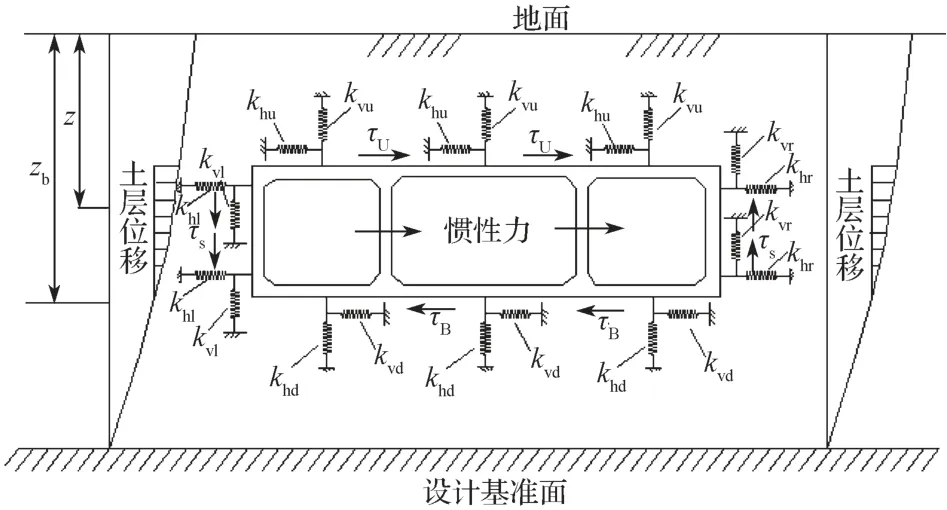
图2 反应位移法计算模型Fig. 2 Calculation model of response displacement method

反应位移法的不足：

1）采用集中弹簧的形式来取代土体，没有考虑各个弹簧之间的耦联作用，并且不管采用解析法、经验公式法还是静力有限元法都难以准确确定土体的弹簧系数；

2）结构的存在将对结构周围附近的土体产生影响，采用自由场的剪应力、加速度与结构实际所受的剪应力和加速度有差别；

3）由于集中弹簧的误差，将导致土层变形等效荷载（式（2））产生较大误差。

反应位移法的优点：

1）采用弹簧的形式来模拟土体对结构的相互作用，比土-结相互作用系数法模型更合理；

2）荷载的施加方式也较土-结相互作用系数法更合理。

4 方法改进

采用拟静力进行地下结构抗震计算时，关键是将地震作用下结构最大反应时的受力状态采用静力形式表达出来，具体如下：

1）约束条件的选取。即计算模型采用的约束条件能够取代周围土体对结构的约束作用。

2）荷载的施加方式。即计算模型所施加的荷载与真实地震作用下所受的荷载一致。

3）结果校核。显然，不论采用怎样的约束条件以及荷载施加方式，都会与真实的地震反应存在误差，所以以上两步并不能精确地达到要求，必须对计算结果进行校核。

由于地震作用下地下结构的内力主要是由变形控制的，因此，本文通过对结构变形的修正来确定结构内力。

对于前两步，本文采用反应位移法进行计算，即采用反应位移法的约束条件以及地震荷载施加方式，而对于第三步，则采用土-结相互作用系数法中所得的结构变形进行校核。具体求解步骤如下：

2）采用2中的土-结相互作用系数由自由场变形来获得结构的变形Δst；

5 算例验证

5.1 计算对象和基本参数

为了验证改进反应位移法的有效性，本文采用0.1gEl-Centro波作为输入地震波，如图3所示。通过改变结构的截面形式、土层刚度以及结构埋深来进行数值计算，计算工况如表1所示。选取的2个地下结构的截面尺寸如图4所示。

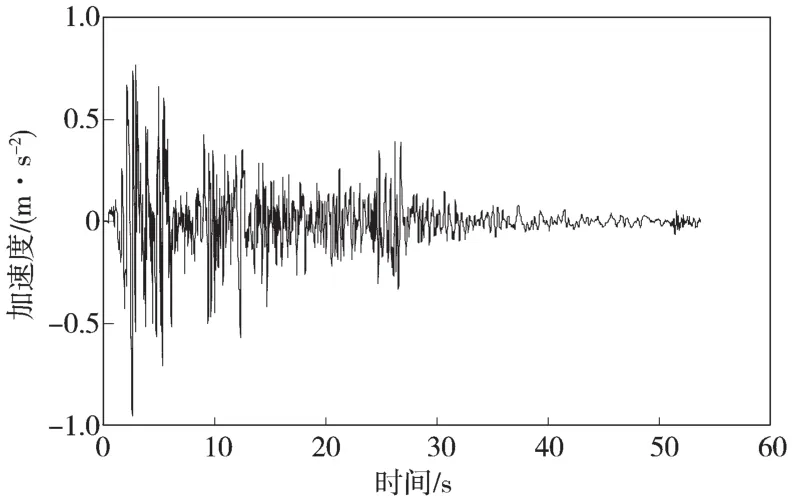
图3 El-Centro波加速度时程Fig. 3 Acceleration time history of El-Centro wave

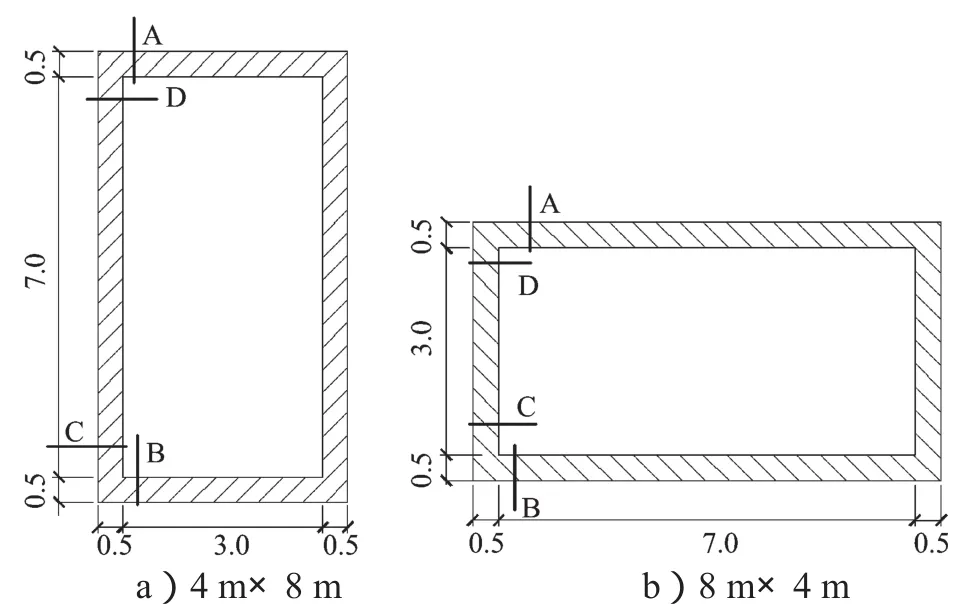
图4 地下结构断面示意图Fig. 4 A sketch map of the cross-section of theunderground structure

表1 计算工况Table 1 Calculation conditions

5.2 计算结果分析

5.2.1 不同截面尺寸

图5和图6分别给出了两种截面形状（如图4所示）的内力图。

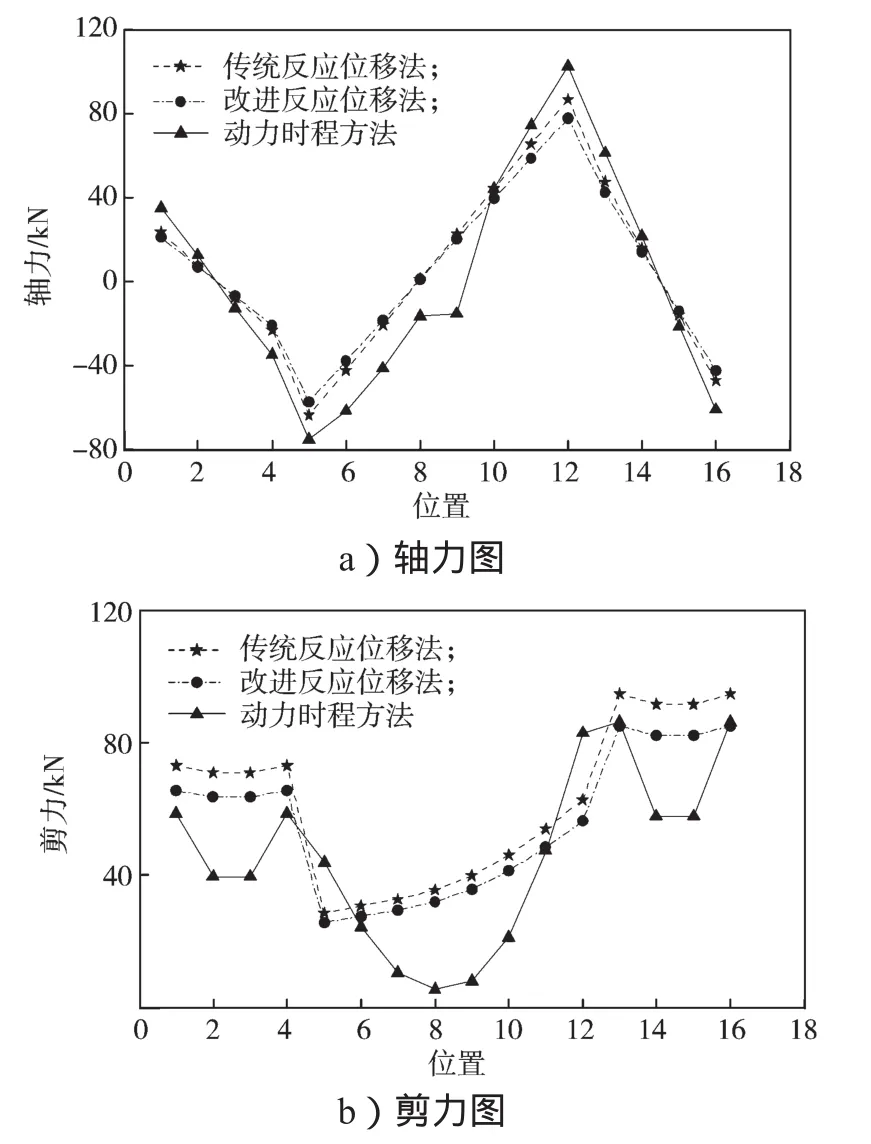
图5 工况1内力图Fig. 5 Internal force chart of case 1

图6 工况2内力图Fig. 6 Internal force chart of case 2

图5和6中，横轴的数字表示结构不同位置，数字含义为从结构左上角编号为1，顺时针绕结构一圈依次编号，共分为24个单元（本文算例中结构左右对称，左右侧墙的内力一样，所以图中只列出右侧墙的内力值），纵轴表示内力值。从图5和6可看出，改进反应位移法只是在传统反应位移法的基础上整体地放大或缩小结构内力，而结构整体的内力分布形式却不改变；在轴力的计算上，改进反应位移法与传统反应位移法相差不大，但在剪力和弯矩的计算上，改进反应位移法要更接近动力时程方法的计算结果。

5.2.2 不同土体刚度

由于篇幅有限，本文只列出关键截面（A、B、C、D）处的内力值，经不同方法计算所得不同土层刚度下的内力结果见表2。从表2所示不同土层刚度下各方法的计算结果可知：整体上来看，改进反应位移法与传统反应位移法的内力计算结果相差不大；当土体刚度较大时（工况5），改进反应位移法和传统反应位移法的内力计算结果与动力时程法的相差较大，特别是体现在轴力的计算上，最大误差可达50%；随着土层刚度的增大，地下结构所受的地震作用减小，所以通过增加土体的刚度，可有效地减小地下结构所受地震作用。

表2 不同土层刚度计算结果Table 2 Calculation results of different soil stiffness

5.2.3 不同结构埋深

不同结构埋深下，经不同方法计算所得的内力结果见表3。从表3所示埋深计算结果可以得知，整体上，改进反应位移法与传统反应位移法的内力计算结果相差不大，幅度在10%以内，但是改进反应位移法的内力计算结果更接近动力时程法的计算结果；当结构处于不同的埋深时，传统反应位移法和改进反应位移法都有较好的内力计算精度；随着埋深的增加，地下结构所受到的地震作用增大，即结构内力增大。

表3 不同埋深计算结果Table 3 Calculation results of different depths of the structure

6 结语

本文通过对土-结相互作用系数法和反应位移法的优缺点进行了分析，并在综合二者优点的基础上，提出了一种基于变形修正的反应位移法。并采用改进反应位移法、传统反应位移法以及动力时程方法，通过改变结构的截面尺寸、土体刚度和结构埋深进行结构受力对比计算，得到如下结论：

1）改进反应位移法整体的计算结果要好于传统反应位移法；

2）改进反应位移法仅整体放大或缩小传统反应位移法的计算结果，不能改变结构内力分布形式；

3）改进反应位移法和传统反应位移法都不适合计算土体刚度较大的工程场地，特别是对于轴力的计算，误差较大，可高达50%。

改进反应位移法通过对传统反应位移法所得到结构变形进行内力修正，理论上来说，这种修订是必要的。但由于反应位移法本身相比理想拟静力法还存在差距，造成结构内力分布仍与动力时程分析方法相差较大，传统反应位移法还有待进一步改进。

[1] HASHASH Y M A，HOOK J J，SCHMIDT B，et al. Seismic Design and Analysis of Underground Structures[J]. Tunnelling and Underground Space Technology，2001，16(4) ：247-293.

[2] WANG J N. Seismic Design of Tunnels：a Simple Stateof-the-Art Design Approach[M]. New York：Parsons Brinckerhoff Quade and Douglas Inc.，1993：53-133.

[3] 立石章. 応答変位法における地震荷重の作用方法 に 関 す る 研 究[EB/OL]. [2016-10-12]. http:// library.jsce.or.jp/ jsce/open/00037/441/441-0157.pdf# search=%27%E5%BF%9C%E7%AD%94%E5%A4% 89%E4%BD%8D%E6%B3%95%E3%81%AB%E3 %81%8A%E3%81%91%E3%82%8B%E5%9C%B0 %E9%9C%87%E8%8D%B7%E9%87%8D%E3%81 %AE%E4%BD%9C%E7%94%A8%E6%96%B9%E6 %B3%95%E3%81%AB%E9%96%A2%E3%81%99 %E3% 82%8B%E7%A0%94%E7%A9%B6%27. TATEISHI A. A Study on Loading Method of Seismic Deformation Method[EB/OL]. [2016-10-12]. http:// library. jsce.or.jp/jsce/open/00037/441/441-0157.pdf#se arch=%27%E5%BF%9C%E7%AD%94%E5%A4%89 %E4%BD%8D%E6%B3%95%E3%81%AB%E3% 81%8A%E3%81%91%E3%82%8B%E5%9C%B0%E9% 9C%87%E8%8D%B7%E9%87%8D%E3%81%AE% E4%BD%9C%E7%94% A8%E6%96%B9%E6%B3% 95%E3%81%AB%E9%96% A2%E3%81%99%E3%82% 8B%E7%A0%94%E7%A9% B6%27.

[4] TATEISHI A. A Study on Seismic Analysis Methods in the Cross Section of Underground Structures Using Static Finite Element Method[J]. Structural Engineering/ Earthquake Engineering，JSCE，2005，22(1) ：41-53.

[5] LIU Rushan，SHI Hongbin. An Improved Pseudo-Static Method for Seismic Resistant Design of Underground Structures[J]. Earthquake Engineering and Engineering Vibration，2006，5 (2) ：189-193.

[6] 刘晶波，王文晖，赵冬冬，等. 地下结构抗震分析的整体式反应位移法[J]. 岩石力学与工程学报，2013，32(8) ：1618-1624. LIU Jingbo，WANG Wenhui，ZHAO Dongdong，et al. Integral Response Deformation Method for Seismic Analysis of Underground Structure[J]. Chinese Journal of Rock Mechanics and Engineering，2013，32(8) ：1618-1624.

[7] 陈国兴，左 熹，庄海洋，等. 地铁车站结构大型振动台试验与数值模拟的比较研究[J]. 地震工程与工程振动，2008，28(1) ：157-164. CHEN Guoxing，ZUO Xi，ZHUANG Haiyang，et al. A Comparison Between Large-Size Shaking Table Test Results and Numerical Simulation of a Subway Station Structure[J]. Journal of Earthquake Engineering and Engineering Vibration，2008，28(1) ：157-164.

[8] 景立平，孟宪春，孙海峰，等. 三层地铁车站振动台试验的数值模拟[J]. 地震工程与工程振动，2012，32(1) ：98-105. JING Liping，MENG Xianchun，SUN Haifeng，et al. Numerical Simulation of Three-Story Subway Station Shaking Table Test[J]. Journal of Earthquake Engineering and Engineering Vibration，2012，32(1) ：98-105.

[9] PENZIEN J. Seismically Induced Racking of Tunnel Linings[J]. Earthquake Engineering and Structural Dynamics，2000，29(5) ：683-691.

[10] WOOD J H，LOWER H T. Earthquake Design of Rectangular Underground Structures[J]. Bulletin of the New Zealand Society for Earthquake Engineering，2007，40(1) ：1-6.

[11] 刘晶波，王文晖，张小波，等. 地下结构横断面地震反应分析的反应位移法研究[J].岩石力学与工程学报，2013，32(1) ：161-167. LIU Jingbo，WANG Wenhui，ZHANG Xiaobo，et al. Research on Response Deformation Method in Seismic Analysis of Underground Structure[J]. Chinese Journal of Rock Mechanics and Engineering，2013，32(1) ：161-167.

[12] 董正方，王君杰，王文彪，等. 基于土层位移差的地下结构抗震反应位移法分析[J]. 振动与冲击，2013，32(7) ：38-42，47. DONG Zhengfang，WANG Junjie，WANG Wenbiao，et al. Response Displacement Method for Seismic Analysis of Underground Structures Based on Soil Layers Displacement Difference[J]. Journal of Vibration and Shock，2013，32(7) ：38-42，47.

[13] 耿 萍，张 景，何 川，等. 隧道横断面反应位移法基本原理及其应用[J]. 岩石力学与工程学报，2013，32（增刊2） ：3478-3485. GENG Ping，ZHANG Jing，HE Chuan，et al. Basic Theory of Seismic Deformation Method in Cross Section of Tunnel and Its Application[J]. Chinese Journal of Rock Mechanics and Engineering，2013，32(S2) ：3478-3485.

（责任编辑：廖友媛）

Research on the Improvement of the Response Displacement Method Based on Deformation Modi fi cation

BIN Jia1，JING Liping2，LI Yongqiang2
（1. School of Civil Engineering，Hunan University of Technology，Zhuzhou Hunan 412007，China；2. Institute of Engineering Mechanics，China Earthquake Administration，Harbin 150080，China）

Based on an analysis made of the soil-structure interaction coefficient method and the response displacement method applied to the seismic analysis of underground structures, an improved response displacement method of deformation modi fi cation has thus been proposed, with the advantages of the former two methods integrated. The improved response displacement method, which is based on the traditional response of the displacement method, makes an modi fi cation of the structural deformation of the reaction displacement method by the deformation of the soilstructural interaction coef fi cient method, thus adjusting the internal force of the structure and reducing the error of the traditional response displacement method. In order to verify the effectiveness of the improved method, a comparative calculation has been made between the traditional response displacement, the improved response displacement method and the dynamic analysis method by altering the dimension of the structure, the stiffness of the soil and the depth of the structure. The results show that: the overall calculation results of the improved response displacement method are more favorable than the conventional response displacement method; the improved response displacement method can generally enlarge or reduce the result from the traditional response displacement method, but cannot change the distribution form of the internal force of structures; there still exists considerable errors in the traditional response displacement method.

underground structure；seismic analysis；response displacement method；soil-structure interaction coef fi cient

TU93；P315.9

A

1673-9833(2017)02-0038-06

10.3969/j.issn.1673-9833.2017.02.007

2016-11-16

国家自然科学基金资助项目（51438004），国家自然科学基金资助青年项目（51408566），中央级公益性研究所基本科研业务费专项基金资助项目（2014B03）

宾 佳（1988-），男，湖南株洲人，湖南工业大学讲师，博士，主要从事地下结构抗震方面的教学与研究，E-mail ：binjia1988@126.com