发掘对称关系,把握求解策略

安徽省池州一中(247000) 吴成强

发掘对称关系,把握求解策略

安徽省池州一中(247000) 吴成强

解题是中学数学学习最重要的思维活动,提高解题能力是广大中学生不断追求的目标.一道较难的题,如果能够顺利求解,无疑是一件很有成就感的事,而如果方法巧妙、新颖,则更给人带来一种美的享受,对思维有很大的启迪作用,特别是能激发学生对创新思维的渴望和追求.解题的方法很重要,所谓方法不对“累死牛”.数学中的解题方法很多,需要我们在解题中不断发掘,不断总结,不断比较,去劣取优.好的方法能迅速帮助学生找到解决问题的突破口,即形成好的解题思路,但这恰是不少学生的困惑所在.针对不同的问题,需要选择不同的方法,这就要求学生的数学功底很扎实.

“对称美”广泛存在于数学之中,数学中有许多问题都具有对称的规律,有些是显性的,有些是隐性的,在解决这类问题中,我们要有一双“慧眼”,善于发掘这种对称规律,并能巧用对称规律,使我们在解题中形成顿悟,产生灵感,找准突破口,并能曲径通幽,层层深入,巧妙求解.本文主要探究如何利用“对称美”探寻解题思路,起一个抛砖引玉的作用.

一、善于发掘对称规律,把握式子变形方向

有些式子的结构隐含着某种对称性,在式子的变形过程中,我们就是要善于发现和抓住这种对称的规律,始终把握平衡与和谐,使式子的变形向着目标逐步靠近,从而使问题得以顺利求解.

思路分析本题看似比较复杂,难以找到问题解决的突破口,但我们若始终以对称与和谐作为式子变形的方向,问题就会柳暗花明,豁然开朗.

证明

(式子有点对称,但还不完全对称,还需要朝着对称的目标继续努力.)

(式子向着对称的方向迈进了一步,但还不完全对称.)

(式子变形到此,应该具有很强的对称性,有一种平衡与和谐的感觉)

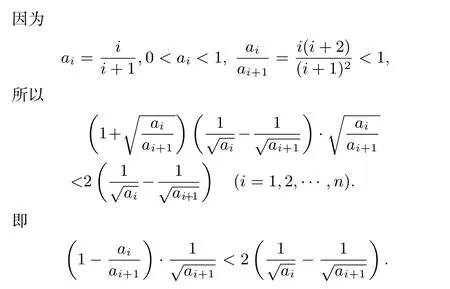
(这个式子符合裂项相消法的要求.)

所以

命题得证.

评注本题可以说是根据对称性探索解题思路和对式子变形的很好的范例.

例2已知f(x)=x2+2(a−2)x−4alnx,若对任意x1,x2∈(0,+∞)且x1＜x2都有求a的范围.

思路分析通过变形,将式子变成左右对称的结构,便于构造新的函数,转化为函数的单调性的问题.

解因为x1,x2∈(0,+∞),且x1＜x2,所以原不等式等价于f(x2)−f(x1)＞2a(x2−x1),即f(x2)−2ax2＞f(x1)−2ax1,(这个式子有一种对称与平衡的感觉.)

评注本题在式子的变形中考虑到能够变成结构对称的式子,从而把相同变量移到式子的一边,得出f(x2)−2ax2＞f(x1)−2ax1这种两边同结构的式子,从而易于构造一个新的函数.这种处理问题的办法也是比较常见的,在高考中也有多次考查.

例3已知x,y,z＞0,且

求证:以x,y,z为三边长可构成三角形.

思路分析许多学生拿到这个题目都感到无从下手,被这个比较复杂的分式“吓着了”.他们尝试着通分,但都因式子过于复杂而变形不下去,还有的想到利用余弦定理,但这显然不行,因为余弦定理在三角形中才能运用,而本题要证的就是能够构成三角形.我们要变形的目标是:x+y−z＞0,y+z−x＞0,z+x−y＞0,这就要一种直觉,要灵机一动,要善于分析捕捉式子的结构特征,要对添“0”法技巧的运用非常熟练.其实,这个式子具有轮换对称技巧,把右边的“1”移到左边,右边变为0,这种变形符合要证的目标,应该说比较合理,比较自然.因为左边有三个分式,只有一个“1”,如果增加两个“1”就对称和谐了,这时用添“0”法(0=1−1)就可轻松破解.

证明由已知可得:

即(x+y−z)(y+z−x)(z+x−y)＞0,易得x+y−z＞0,y+z−x＞0,z+x−y＞0,所以,以x,y,z为三边可构成三角形.

评注这个证明太巧妙了,把看似非常复杂毫无头绪的问题,通过添“0”法这么一个小小的变形就轻而易举的解决了,真的是很美、很妙!数学中非常讲究式子的变形,往往一个小小的变形,会给人带来意想不到的效果!

二、观察对称结构特征,选择合理化归途径

有些式子从形式上看就具有某种对称特征,解决这类问题就是要以对称性为考虑问题的线索,处处考虑对称、平衡,选择合理的化归途径,把不同的量化归到某一个或某几个固定的量上来,使问题求解变得目标明确,式子变形或化简变得简单.

例4已知O为△ABC内任一点,求证:

思路分析不少学生拿到这个题目后感到无从下手,特别是式子中将三角形面积与向量综合到一起,学生更是有一种“恐惧感”.其实,这个题目从结构形式上看具有很好的对称性,所以我们应该从对称的角度来分析,在式子的变形过程中考虑对称性,变形的最终结果也将具有对称性.作出图形(如图1).

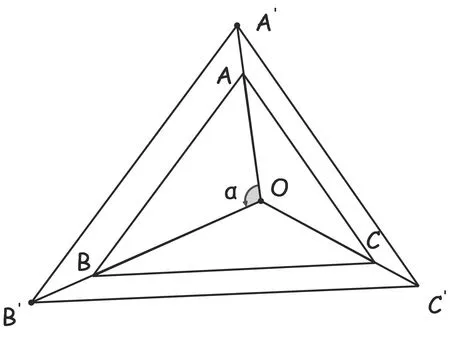
图1

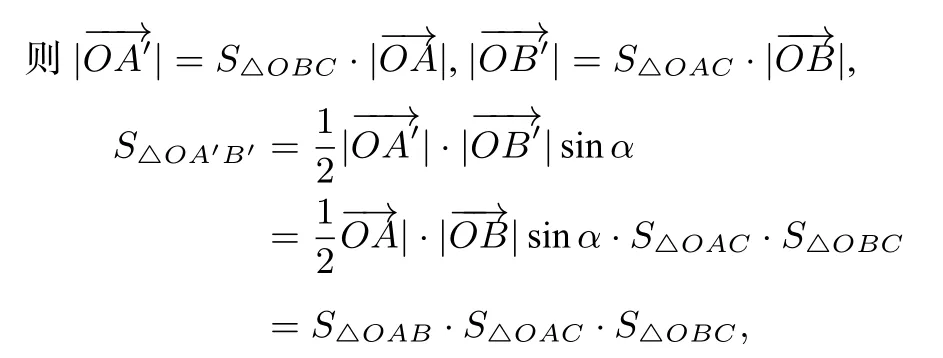
同理可得:

证法二考虑到平面向量的基本定理,平面上任一向量都可以用两个基向量作为基底唯一表示,这样,就可将其它向量统统转化为用这一组基底向量表示,从而减少向量的种类,便于消元.

图2

评注(1)本题中的两种证法都是建立在基本功比较扎实,有一定的解题经验的基础上的.解题要善于抓住对称性这一特征,找到解决问题的正确思路,从而使问题顺利求解.

(2)证法一是构造了一个新的三角形,并且得到了一个很好的结论:S△OA′C′=S△OB′C′=S△OA′B′=S△OAB·S△OAC·S△OBC,这个结论具有统一性.证法二则是将所有向量统一到两个基向量上来,减少变量,便于化简,思路简朴,让人感到情真意切,朴素大方.

(3)根据结构的对称性,可作如下的类比推理:若为三棱锥内任一点,则

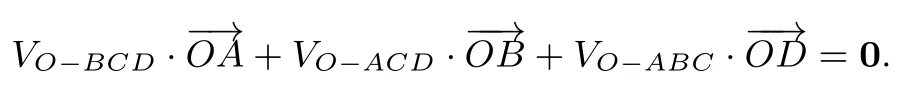
此题的证明可以完全类比上述的证明.

三、抓住图形的对称性,问题求解直观又简单

数学中有许多函数的图像或方程表示的曲线都具有对称性,如正态分布密度曲线就是轴对称图形,解析几何中的椭圆是中心对称图形.我们要善于利用这些图形的对称性,挖掘其中的隐含条件,巧妙地解决问题.

例5正方体ABCD−A1B1C1D1的各顶点及各棱中点共20个点中,任取两点连成直线,则这些直线中与平面A1BC1平行的直线有( )

A. 9条 B. 18条 C. 21条 D. 24条

图3

思路分析如图3,与平面A1BC1平行的直线应该与平面A1BC1内的某一条直线平行.自然先找与边BA1平行的直线,易找出与边BA1平行的直线有6条,根据对称性,同理可得与边BC1平行的直线有6条,与边A1C1平行的直线有6条,此时与边平行的直线共有18条.于是不少学生可能选择B答案.我们还应该作更深一点思考,除了上述18条直线外,还有没有其他直线呢?如果有,它究竟应该和平面A1BC1中哪条直线平行呢?根据图形的对称性,容易分析如果有,肯定与△A1BC1的中线平行.如图3,与中线BO平行的直线有EE1、FF1,同理与另外两条中线平行的直线也各有2条.故与中线平行的直线共有3×2=6条.因此共有18+6=24条,故选D.

评注立体几何有许多图形具有对称性,我们若能抓住对称性,往往能很快找到正确的解题方向.

例6已知△ABC的一个顶点A(4,−1),其内角B、C的平分线方程分别为y=x−1和x=1,求边BC所在直线方程.

思路分析本题应考虑角平分线的对称性质.A点关于∠B平分线的对称点A1在边BC上,A点关于∠C平分线的对称点A2也在边BC上,这样直线BC的方程就是直线A1A2的方程.

解易得A(4,−1)关于∠B的平分线y=x−1的对称点A1的坐标为(0,3),A(4,−1)关于∠C的平分线x=1的对称点A2的坐标为A2(−2,−1),A1A2的方程为2x−y+3=0,所以BC边所在直线方程为2x−y+3=0.

评注本题就是利用对称性,使问题解决变得较为简单,给人以美的享受和思维的启迪.但不少学生对角平分线隐含的对称的性质不太熟悉,自然就想不到利用对称性来求解,从而使问题求解变得非常麻烦.本题再一次展示了“对称美”在解题中的指引灯塔的作用.

四、利用对称性,对结论进行合理而大胆的预测

有些问题如果盲目求解,可能使式子的变形或运算变得相当复杂,甚至于得不到结果.所以遇到这类问题往往要先根据条件作出合理判断,再来对结论进行验证,可大大减少运算量.根据对称性作出预判,在解析几何中最为常见,应该成为解题的一条重要经验和法宝.

例7已知椭圆=1的上顶点A(0,2),下顶点B(0,−2),直线y=kx+4与椭圆交于M,N两点,直线AM与BN相交于Q点,求证:Q点在一条定直线上.

思路分析因为直线y=kx+4恒过定点(0,4),且直线可在y轴的两侧运动,如果Q点在一条定直线上,根据对称性易知,此定直线应该为平行于x轴的直线.

证明设M(x1,y1),N(x2,y2),则有

联立①②消去x得

所以3y−6=−y−2,y=1,即Q点在定直线y=1上.

评注本题就是根据对称性判断Q点在平行于x轴直线上,根据这一预判,想到Q点的纵坐标是一定值,而横坐标任意,从而由①,②两式消除x保留y,这一变形实在是太妙了!这就是合理猜想的结果,它明确了式子变形的方向,避免了运算的盲目性,大大减少计算量,确实令人鼓舞,拍手称好!本题如果没有根据这种“对称美”进行合理猜想,而是盲目运算,很难想象能算出正确结果.事实上,很多学生做这道题时有畏惧心理,他们不知道如何变形,再加上字母运算的复杂性,导致他们没有信心往下算,当然这道题也就不得求解了.圆锥曲线中的很多问题都有一定的内在规律,在解决问题时,要善于分析其内在规律,并进行合理猜想(如本题就是根据对称性进行合理猜想),使计算有一个正确的目标,更加趋向合理和简便.

五、利用对称性,对结论的正确性进行直觉判断

在解决有关问题时,由于我们只考虑部分条件,而忽视隐含在问题中的另一部分条件,思维不够深刻,导致所得结论不全面、不严谨、不合理.如果我们对“对称美”的应用有一定的经验积累,并且有很强的思想意识,那么我们在解决问题的时候就会自觉地运用对称美来判断和检验所得结论的合理性,做出正确的判断和修正.

评注不少同学往往只得出①、②两式中的某一个式子,从而得出的范围是题中给出的式子具有某种对称关系,因而得出的范围也应该具有对称关系,不对称答案肯定有问题.再者,因为−1≤cosα≤1,−1≤sinβ≤1所以cosα·sinβ的范围应该是[−1,1]的子集,而明显不符,所以我们在解题中要具备起码的直觉思维.

狄拉克说:“我们应当把数学美作为我们的指引灯塔,去建立有意义的理论—首先它们得具备数学美.”本文主要探究了“对称美”在解题中的引路作用.其实,“对称美”在概念、定理、公式、法则等多方面都有广泛的应用.可以说,“对称美”是我们解决数学中有关问题的指引“灯塔”,我们在问题解决中要善于挖掘数学中的“对称美”,欣赏数学中的“对称美”,应用数学中的“对称美”,使之成为我们解决问题的利器和法宝.

[1]杨列敏,刘国良.三角形五心向量形式的探究教学[J].中学数学教学参考(上),2016(7):44-45