两主两从博弈下的装备维修器材供应链协调研究
林 翔
(海军装备研究院,北京 100161)
【后勤保障与装备管理】
两主两从博弈下的装备维修器材供应链协调研究
林 翔
(海军装备研究院,北京 100161)
以相互竞争的两条装备维修器材供应链作为研究背景,提出了一种基于Stackelberg主从博弈的激励协调模型,并通过最优反应动态思想给出求解该模型的一般思路,结合粒子群优化算法对军事算例进行仿真,对比分析供应商合作与非合作下的计算结果,供应商非合作下奖金激励策略可以有效实现供应链协调,但供应商若能实现合作,将使供应商达到利益最优化,可忽略奖金激励的影响。
装备维修器材;Stackelberg主从博弈;供应链;最优反应动态;粒子群优化算法
在市场经济条件下,部队作为装备维修器材供应商的最终消费者,其偏好决定了供应商的收益。在供应器材品质相当的情况下,维修单位作为部队与供应商的中间环节,其服务水平是引导部队消费的重要环节。因此,供应商需要提供一定的激励机制提高维修单位的服务水平。
文献[1]给出了当前装备维修器材供应链的一个基本现状以及未来的发展趋势;文献[2]描述了在随机性需求、需求对服务水平敏感条件下,生产商如何通过激励机制使分销商保持较高库存的库存决策问题。文献[3]在假设一个供应商、一个分销商且市场需求确定的情况下,讨论了供应商能够提供几类契约以及对供应链相应的影响。文献[4]讨论了在两个供应商对两个分销商情况下,价格促销对市场需求变化的作用。不足的是,市场需求不仅与商品价格、品质有关,同时也与分销商服务水平相关。文献[5]研究了两个分销系统(每个分销系统具有一个作为主方的生产商和一个作为从方的分销商)发生相互竞争的问题。文献[6-8]提出了一种求解双矩阵对策多重纳什均衡解的粒子群优化算法,并通过仿真示例验证了其有效性。
在上述文献的基础上,结合当前装备维修器材供应实际,给出了两条装备维修器材供应链在Stackelberg博弈下的协调订货问题,并在此基础上建立优化模型,构建适应度函数,利用粒子群优化算法求解,并运用实际算例进行了仿真计算,对两主方合作与非合作的情况进行了对比分析,得出了一些可以解释现实中出现的经济状况的结论。
1 问题描述
对同一类武器装备,往往有多个维修单位对同一军事片区进行维修保障,同时,这些维修单位又分别有自己的装备维修器材供应商,供应商要想将自己的装备维修器材尽量多的供应给部队并从中获取收益,就需要所供应的维修单位尽量多的接手到相应的维修任务,消耗掉装备维修器材,从而有新的订单来为供应商获取利润。
同一军事片区内的部队,在遇到武器装备故障问题时,会综合考虑维修费用、维修品质和维修服务态度等因素决定维修单位,其中的维修服务态度是变数最大的,与维修单位对每个维修任务的重视程度有直接关系,包括说明故障问题、纠正使用方法、定期派人维修保养等。因此,供应商为了让维修单位提供尽可能让部队满意的维修服务态度,建立激励机制[9]鼓励维修单位改善服务态度,提高维修单位认可度,获得在承受范围内更多的维修任务。
2 建立激励协调模型
2.1 模型假设与分析
本文通过分析同一军事片区内的两条装备维修器材供应链分析上述问题,假设某舰艇支队的维修保障任务都可由这两个维修单位负责。供应商根据维修单位一个周期内所用的装备维修器材数量提供奖金,用σ表示单位数量的奖励,而维修单位则通过提高服务水平争取尽量多的维修任务,获取奖金。显然,服务水平的提高需要维修单位付出相当程度的努力,这里用η表示维修单位的努力程度。
面对同一军事片区内有限的维修任务,两个维修单位之间就会产生竞争关系,维修单位B1在确定自己的努力程度时,不仅要考虑供应商提供的奖金,还要考虑维修单位B2的努力程度。因为一方的努力程度明显高于另一方,就会出现大部分维修任务被一方占据的情况。若维修单位B2的努力程度越高,其维修任务自然会更多,此时供应商A1在制订激励策略时不仅要考虑维修单位B1,还需要把维修单位B2的努力程度考虑在内,并进一步考虑供应商A2的激励策略。同样地,维修单位B2和供应商A2也面临同样的策略问题。这两条装备维修器材供应链相互影响的示意图如图1。

图1 两装备维修器材供应链相互竞争示意图
显然维修单位Bi(i=1,2)的努力程度ηi(0≤ηi≤100%)需要付出相应的努力成本Ci,并且努力成本Ci是努力程度ηi的严格增函数,随着ηi的递增,Ci递增速度更快,即Ci′(ηi) > 0,C″i(ηi) > 0,该成本函数可以用公式表示[10]:
(1)
其中ci是一个定值。
维修单位一个周期内所获的维修任务可以通过这一个周期所使用的装备维修器材数量Γ来体现,在此假设部队选择维修单位时对服务水平相当敏感,维修费用影响不大,且维修单位的维修品质都很平均。可以得出,器材使用函数Γ与维修单位的努力程度密切相关,不仅与自己的努力程度有关,也与另一个维修单位的努力程度有关。当对手的努力程度不变时,自己的努力程度越大,就能争取到可能原本属于对手的维修任务,维修任务多了,装备维修器材使用数量自然也就越大,可以用下式表达其含义:
(2)
其中i,j∈{1,2}且i≠j,αi为自身努力程度对装备维修器材使用数量的产出系数,β为努力程度差值对装备维修器材使用数量的转移系数,即当ηi>ηj时,维修单位Bj的装备维修器材使用数量β(ηi-ηj)转移给维修单位Bi,当ηj>ηi时,情况刚好相反。
为简化模型,将维修单位使用的装备维修器材数量作为供应商可以得到收益的装备维修器材销售数量。并且不考虑各成本与收益之间的复杂关系,只关心奖金激励与努力程度对两条装备维修器材供应链中供应商和维修单位的影响。
可以得出供应商Ai的总收益为
(3)
维修单位Bi的总收益为
(4)
其中ai为供应商Ai的单位装备维修器材销售利润,bi为维修单位Bi使用单位装备维修器材的维修收益。
2.2 Stackelberg主从博弈问题
根据上述分析,这两条相互影响的装备维修器材供应链构成了两主两从的Stackelberg主从博弈问题,其中主方是供应商A1、A2,策略就是奖金激励策略;从方是维修单位B1、B2,用努力程度响应。用U和V分别表示主方和从方的策略集,奖金激励策略σ1、σ2表示主方A1、A2的策略,努力程度η1、η2表示从方B1、B2的策略,即σ1,σ2∈U,η1,η2∈V。
两个主方、两个从方作为独立的利益主体,都希望达到利益最大化,所以供应商Ai的策略函数为
(5)
维修单位Bi的响应函数为
(6)
式(5)(6)所得的决策对({σ1,η1},{σ2,η2})就是上述两主两从Stackelberg主从博弈问题的均衡解。
2.3 优化模型
显然,供应商作为纯粹的利益组织,其目的就是为了获取更高的利益,所提供的奖励不可能高于销售利润,即
(7)
为简化问题,假设两供应商相互合作,上述两主两从的Stackelberg主从博弈问题实际就变成了一主两从的Stackelberg问题。以两供应商总收益最大化为目标,通过两从方之间努力程度的相互制约来建立约束关系,可以得到一主两从的Stackelberg模型如下:
(8)
而对两主方完全非合作的两主两从Stackelberg主从博弈问题,需要分别以两供应商收益最大化为目标,建立多目标优化模型如下:
(9)
(10)
该模型是一个多目标非线性约束问题,本文利用进化博弈论的最优反应动态思想(Best response Dynamics)[11-12]与粒子群优化算法,对上述两主两从的Stackelberg主从博弈问题进行求解。
3 算法设计
通过文献[11-12],可以知道利用最优反应动态思想,可以很好地模拟有限理性人的行为,在竞争者进行策略迭代时逼近Stackelberg主从博弈的均衡解。在两主两从Stackelberg主从博弈问题中,两主方是通过两从方的竞争策略来进行相互博弈,主方与从方构成一个上下层关系,之间的博弈为Stackelberg博弈,而下层两个从方之间的博弈为Nash博弈。
求解两主两从Stackelberg主从博弈模型,实质上是对从方相同的两个一主两从模型进行求解,其求解过程如下:
步骤1 初始化上层(主方)策略σ;
步骤2 下层(两从方)根据各自目标函数最大化进行多目标优化问题求解,得到一个Nash均衡解,作为下层(两从方)的策略{η1,η2};
步骤3 利用粒子群优化算法,以上下两层即主从双方的策略代表粒子,进行一主一从下的Stackelberg主从博弈模型求解。
利用上述过程可以求出两主方合作下的均衡解,需要注意的是,供应商在由非合作转换成合作的过程中,应具备一个基本的触发条件,即保证供应商在非合作下的利益低于合作后的利益。因此,为维持合作的稳定性,需要制订一个合作方均能认可的利益分配方案,本文采用的是核和Shapley值的利益分配方案[13]。
假设Stackelberg博弈中的两从方是完全理性的,其决策是同时进行的,并假设主方是有限理性的,以保证主方提出策略后,从方能迅速给出依据主方策略的均衡解。下面给出采用进化博弈论中的最优反应动态思想求解两主两从Stackelberg问题的算法步骤:
步骤1 初始化供应商A1、A2给维修单位的单位数量奖金策略σ1、σ2。
步骤2 给出主方A1、A2之间的行动顺序,同时设定决策的最大迭代次数kmax,记k=0。对于主方行动顺序有先后的情况,转到步骤3,对于同时行动的情况,转到步骤4。
步骤3 利用一主两从Stackelberg问题的求解思路,在每轮决策中,主方Ai根据Aj的策略,考虑从方B1、B2的反应,做出新的策略来替换原策略,而主方Aj决策时,再根据主方Ai新策略下从方B1、B2的反应来制定其新策略,替代原策略,这样迭代次数才算完成一次,即k=k+1。
步骤4 利用一主两从Stackelberg问题的求解思路,在每轮决策中,主方Ai(i=1,2)决策时,根据另一主方的策略,考虑从方B1、B2的反应,制定新的策略。当主方A1、A2都决策完毕了,再用两个新策略来替换原策略,这样本轮决策完毕,迭代次数加1,即k=k+1。
步骤5 对于主方行动顺序有先后的情况,重复步骤3,而对于主方同时行动的情况,重复步骤4。直到两个主方该轮决策结果与上一轮的相同(或两者之间的范数小于给定值),则达到Stackelberg均衡,算法结束。或者是当迭代次数k=kmax时,算法终止。
4 军事算例仿真与分析
在某一军事片区中有两个维修品质和维修水平相当的维修单位B1、B2,他们各自都有自己的器材供应商,其中供应商A1负责维修单位B1,供应商A2负责维修单位B2,两维修单位处于独立非合作关系。两维修单位全面负责该军事片区中联轴节等这类装备维修器材的保障维修任务,因为联轴节等这类器材耗损率高,耗损速度快,报修周期短,故该军事片区中的部队用户对维修单位的维修服务水平较为敏感,该军事算例的基本参数设置如表1所示。

表1 有关参数
初始化主方的策略σ1=σ2=0,即两个供应商刚开始都不给维修单位提供奖金激励,在此初始条件下,利用最优动态反应思想与粒子群优化算法对两供应商合作与非合作下的Stackelberg主从博弈模型进行求解,其中取粒子群规模N=20,参数设定ωmax=0.9,ωmin=0.4,最大迭代次数kmax=50。仿真计算实现采用的操作系统为Windows XP,机器硬件CPU为Pentium Dual-Core 3.0 GHz,2 GB内存,用Matlab 7.1编程计算,计算时间不超出3 s。所得结果如表2所示。

表2 合作与非合作下求解结果对照
其中,在供应商非合作决策下,A1先决策A2后决策、A2先决策A1后决策以及二者同时决策3种情况求解得到的Stackelberg均衡解都是
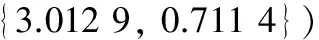
(11)
当A1、A2不同时决策时,求解到第2轮迭代后就已经接近Stackelberg均衡解,而A1、A2同时决策时,要到第3轮迭代结束才接近均衡解,这说明多个主方决策顺序是否相同与最后求得均衡解的速度有一定关系。
观察表2可以得出以下结论:
1) 在供应商合作的情况下,供应商不会提出奖金激励。
2) 在供应商非合作的情况下,供应商会提出奖金激励以提高维修单位努力程度。
3) 供应商非合作下,维修单位的收益要高于合作下的收益,表明维修单位可以在供应商非合作中渔利。
4) 供应商在合作下的总收益要高于非合作下的总收益,且当6 981≤t≤7 726时,各供应商合作后的收益均大于非合作下的收益,故供应商有发起合作的基本动机,并在t=7 354时达到Shapley值。但具体利益分配方案会受到合作行为、公平性要求以及其他非理性情感因素的影响,要综合考虑Shapley值进行谈判决定。
5) 供应商在非合作下提出奖金激励能使维修单位收益增加,似乎牺牲了自己的利益,因为在供应商合作下,即使不给维修单位提供奖金激励,供应商的利益也比非合作下的高。可惜的是σ1=σ2=0并不是Nash均衡,还需要两个主方的共同协作来达成。这也正好与当今市场下主导者时常提出奖金激励制度的现状相吻合,原因就在于市场中主导者进行合作时要达到Nash均衡非常困难。
5 结束语
本文以维修单位独立非合作为前提,分析了同一军事片区中同类武器装备的两条装备维修器材供应链相互竞争的关系,提出了两主两从Stackelberg主从博弈问题,并建立相应的多目标优化模型。最后,应用进化博弈论中的最优动态反应思想结合粒子群优化算法给出两主两从Stackelberg问题的求解步骤,利用军事算例进行仿真,对供应商合作与非合作下的结果进行分析,得出:在非合作下供应商实施奖金激励策略可以实现供应链协调,而在合作下奖金激励不再那么重要,关键在于如何实现供应商的合作共赢。
[1] 何海宁,舒正平.供应链环境下的装备维修器材保障[J].物流科技,2006,136(29):66-69.
[2] RICARDO E,STEPHEN G P.Manufacturer Incentives to Improve Retail Service Levels[J].European Journal of Operational Research,1998,104(11):437-450.
[3] CORBETT C J,TANG C S.Designing Supply Contracts:Contract Type and Information Asymmetry[M].Chapter 9 in the Quantitative Models for Supply Chain Management,Boston,Kluwer:1999.
[4] LAI R,VILLAS-BOAS J M.Price Promotions and Trade Deals with Multi Product Retailer[J].Management Science.1998,44(7):935-9491.
[5] 田厚平,郭亚军,刘长贤.分销系统中的多主多从Stackelberg主从对策问题研究[J].管理工程学报,2005,19(4):74-78.
[6] 张荣沂.一种新的集群优化方法—粒子群优化算法[J].黑龙江工程学院学报,2004,18(4):34-37.
[7] 瞿勇,张建军.多重纳什均衡解的粒子群优化算法[J].运筹与管理,2010,19(2):52-55.
[8] 马向阳,陈琦.以粒子群算法求解买卖双方存货主从对策[J].中国管理科学,2010,18:142-145.
[9] 罗定提,仲伟俊,张晓琪.分散式供应链中旁支付激励机制的研究[J].系统工程学报,2001,16(3):236-240.
[10]张维迎.博弈论与信息经济学[M].上海:三联出版社,1996:182-186,190-197,200-207.
[11]谢识予.经济博弈论[M].上海:复旦大学出版社,2002:268-273,244-245.
[12]盛昭瀚,蒋德鹏.演化经济学[M].上海:三联出版社,2002:13-17,281-285.
[13]LEOPOLD W U.Some Selected Topic in Experimental Economics[J].International Transactions in Operational Research,1997,4(3):165-174.
[14]林翔, 瞿勇. 基于主从博弈的装备维修器材供应链协调订货[J].兵工自动化,2015(12):59-63.
[15]高铁路,叶术青,高崎.基于价值的装备维修器材保障风险研究[J].四川兵工学报,2015(11):70-73.
(责任编辑 唐定国)
Study on Supply Chain Coordination of Equipment Repair Equipment with Two Leaders-Followers Game
LIN Xiang
(Naval Academy of Armament, Beijing 100161, China)
Take the competitive two supply chain of equipment repair equipment as the research background, a kind of incentive coordination model based on the Stackelberg game is proposed, and the general idea of solving the model is given by using the best response dynamics theory. Through the application of the particle swarm optimization algorithm (PSO), the simulated results of the military example on the suppliers cooperation and non cooperation are analyzed to show that the incentive strategy under the non cooperation can effectively achieve the coordination of the supply chain, but if the suppliers to get the cooperation, it will enable the suppliers to achieve the best interests of the optimization and the bonus incentive is no longer the key.
equipment repair equipment; Stackelberg game; supply chain; best response dynamics; PSO algorithm
2016-12-21;
2017-01-16 作者简介:林翔(1991—),男,硕士,助理工程师,主要从事军事建模与系统决策研究。
10.11809/scbgxb2017.05.032
format:LIN Xiang.Study on Supply Chain Coordination of Equipment Repair Equipment with Two Leaders-Followers Game[J].Journal of Ordnance Equipment Engineering,2017(5):140-143.
O225
A
2096-2304(2017)05-0140-04
本文引用格式:林翔.两主两从博弈下的装备维修器材供应链协调研究[J].兵器装备工程学报,2017(5):140-143.

