贷款定价的基本模型

张志强

一、贷款定价问题的理解

常有人认为，利率市场化就是银行随行就市确定贷款的利率。笔者认为，这样的理解并不完全正确。发放贷款不同于在市场上买卖一般的商品。在市场上出售一般的商品比较简单，所谓随行就市也就是参照别人的售价，自己也定个差不多的价格就可以了。但是，贷款发放的情况就不同了。银行在决定一笔贷款的利率时，不能仅仅依照市场上其他银行的定价，就据此定价。这是因为，一是其他银行的定价可能差异很大，没有统一标准；二是难以弄清楚其他银行定价差异的原因，因为贷款定价的重点也是难点是确定对贷款的风险补偿。

理论上讲，即便是同一家银行对同一家企业的贷款，第一笔和第二笔贷款的风险也是不一样的，这就意味着第一笔和第二笔贷款应该定不同的价格。实践中银行家也许可以意识到，一般情况下（如第一笔贷款利率合理），第二笔贷款应该比第一笔贷款利率高，因为企业的负债率会随着贷款的发放而增加，而企业的负债率是影响银行风险的重要因素。那么，究竟应该高多少呢？市场无法提供一个基本准确的数字答案，银行家的经验或主观判断也无法提供一个基本准确的数字答案。

贷款定价即贷款利率如何确定的问题，是一个典型的金融问题。银行贷款定价的目的是合理回避和补偿风险，同时又在竞争中不损失客户和机会，从而最大限度地获得经营收益。对于这样的问题，首先应该通过金融理论研究，得出利率取决于哪些重要或基本因素，与这些因素的定量关系是什么，即得出利率决定的理论模型；然后，探讨这种考虑基本因素的理论模型如何在实践中应用。本文下面就致力于探讨利率决定的理论模型，抛砖引玉，以期给读者以参考和启迪。

二、贷款的风险与贷款利率的构成

笔者认为，学术的专业体现在用最少的而不是最多的变量和数据以及最简洁而不是最复杂的方式解决问题。当然，作为定量科学，金融研究肯定需要数据，但不是靠数据解决问题；而是在有了理论模型的基础上（问题得到解决后），需要代入有关基础变量的数据得到结果（如贷款的利率）。究竟需要哪些基础变量数据，这些数据与结果之间是什么定量关系，这些问题都需要金融理论研究基于专业逻辑而不是靠统计数据来解决。

贷款定价是一个典型的金融问题，那么我们就按照金融的专业逻辑来探讨。根据上述分析，首先应该对银行贷款的风险进行深入的探讨。

银行发放贷款会面临风险。传统上认为银行贷款面临多种风险，主要包括通货膨胀风险、流动性风险、贷款期限风险以及违约风险。本文先不探讨这些风险的定义，而是先梳理有关的金融逻辑。以贷款定价问题为导向，首先值得考虑的是，一笔贷款发放前后，银行会关心和担心什么？或者，对于所发放的一笔贷款，银行应该或可以有哪些合理的要求？

笼统地说，银行的要求包括如期收回本金和利息，这也是银行关心和担心的事情。能否如期如数地收回本金和利息并不确定，这就是银行所冒的风险。可以理解，这些风险需要通过确定的利息（利率）得以补偿。银行收回本金要求的合理性不说自明。需要考虑的是，银行收回利息的要求在什么范围内是合理的呢？

首先，即便贷款没有风险，将钱贷给企业用，也理所应当收取利息。但就合理性而言，银行不冒风险，也就只能按无风险利率收取利息。这部分利息是对银行资金的纯时间补偿，也就是对银行资金失去流动性的补偿。需要说明的是，在未来贷款持续时间中有可能发生通货膨胀，这意味着货币会贬值，这显然不利于作为债权人的银行，为此银行应该要求无风险利率中包含有对预期通货膨胀的补偿。所以，贷款利率中应该有一部分是无风险利率，其中包含了对通货膨胀和流动性风险的补偿。

其次，现实中的贷款当然都是有风险的，这意味着在无风险利率的基础上，贷款利率中还应该包含风险的补偿。与无风险的贷款相比，普通银行贷款有什么风险呢？虽然现实中命名了多种风险，但其实只有一种风险，即不能如期收回本息的风险，也就是违约风险。那么，期限风险就不考虑了吗？期限风险意味着贷款期限越长，违约风险越大。所以，期限风险只是违约风险的一个因素而已。

综上所述，贷款利率应该由无风险利率和违约风险补偿率两部分组成。这就意味着要正确确定贷款利率，就要分别正确确定无风险利率和违约风险补偿率。无风险利率可根据同样期限的政府债券期望收益率确定，这在金融领域是已经解决的问题。所以，需要探讨解决的问题就是如何确定违约风险补偿率。

三、违约风险成本与贷款利率——ZZ利率模型

金融是研究资产价值的学科，根据资产的价值得出决策结论。金融的常规计算是根据未来收益计算资产的价值。与收益对应的是风险，收益可以带来价值的增加，风险则会带来价值的减少。所以，金融也需要计算风险的价值，实际是风险带来的负价值，或可称为风险成本。不仅如此，金融有时候还需要做价值的逆运算，即根据资产或风险的价值得出未来各期的应得收益或需要补偿的成本。

明白了金融科学上述的基本定量功能，也就可以理解，如果能计算出贷款违约风险的成本，就可以通过将其分解得到各年的应得利息，再除以本金即得各年的违约风险补偿率。当然，这个思路成功的关键是能否计算出贷款违约风险的成本。在金融领域，除了有钱不还的道德原因导致的违约，违约与破产几乎是等同的概念。也就是说获得贷款的企业之所以会违约，是因为企业确实因经营不善而资不抵债从而无力偿还贷款本息。所以，违约风险的成本也可称为破产风险的成本，或简称破产成本。

破产成本在金融领域是一个长盛不衰的研究热点。1958年Modigliani和Miller推导建立了关于资本结构的MM模型I1Modigliani, F. and M. H. Miller, 1958, “The cost of capital, corporation fi nance and the theory of investment”, American Economic Review 48, 261-297.，点燃了金融学者解决最优资本结构问题的热情。由于破产成本是攻克最优资本结构问题的一个关键点，50多年来，一直有学者对此进行研究。2009年，张志强更正了概念理解的错误，利用期权定价方法推导建立了破产成本模型2Zhiqiang Zhang, Determining the optimal capital structure based on revised def i nitions of tax shield and bankruptcy cost, Frontiers of Business Research in China, 2009, 3(1), 120-144.，解决了破产成本的计量问题，并进一步推导出最优资本结构模型。

所以，可以基于ZZ破产成本模型来推导贷款风险补偿率，该模型形式如下：

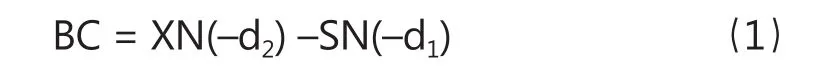
式（1）中，BC 代表破产成本；S代表公司目前价值；X代表企业债务的本金，同时遵循研究惯例，假设它等于债务的现值；N (–d2)和N (–d1)分别代表标准正态分布中变量值取–d2和–d1时的累积概率。其中，d1和d2可分别按式（2）、（3）求得。

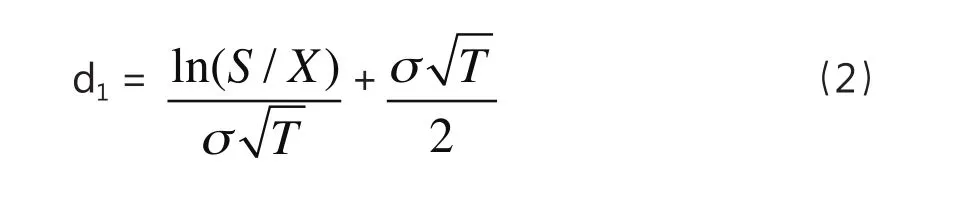
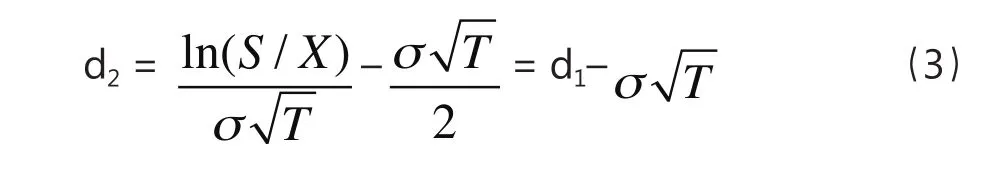
其中：T为企业债务的平均期限（年）；为公司价值的波动率，传统行业的经验值在20%-40%，高科技行业会更高些。

ZZ破产成本模型是针对企业负债融资研究破产成本的问题。贷款即是企业的债务，所以，可以（暂时）将企业债务与银行贷款等同理解。

可以理解，有风险贷款的价值 = 无风险贷款的价值－破产成本。

在不考虑风险即无风险的情况下，贷款的当前价值为X；用c表示贷款的年风险补偿率（不包含无风险利率），注意贷款到期时间为T，则有风险贷款的价值为Xe-cT。因此：

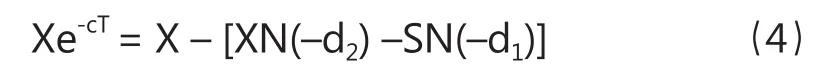
根据式（4）不难求得风险补偿率c。即：

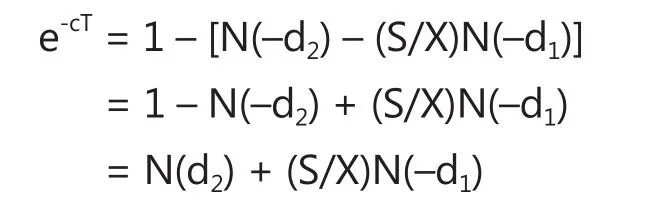
上式两边取自然对数，

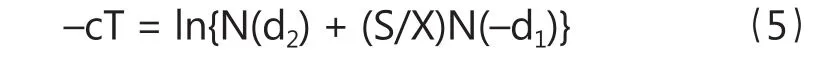
定义公司的债务比率L = X/S，则S/X=1/L，从而，

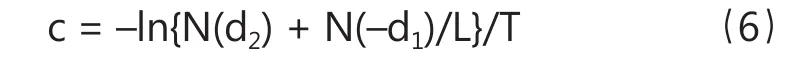
其中，对照式（2）和（3），

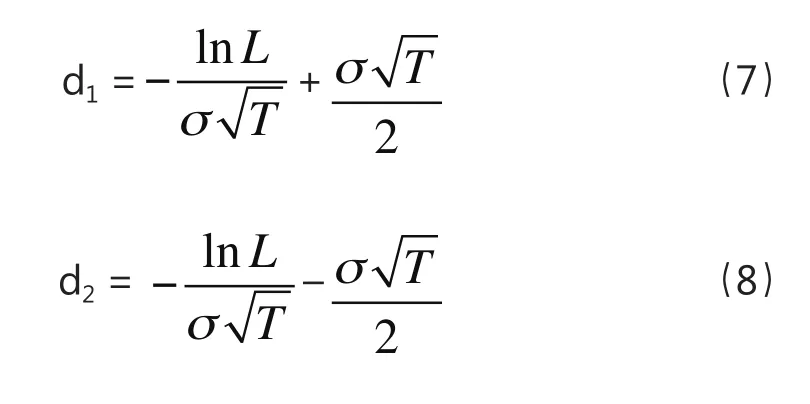
式（6）即是基于ZZ破产成本模型推导的贷款风险补偿率模型，区别于其他模型，可称之为ZZ贷款风险补偿率模型。在此基础上，不难写出贷款利率模型，即：

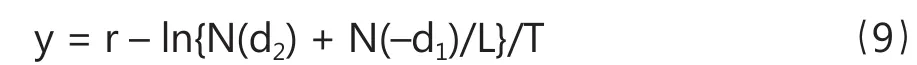
根据式（7）、（8）和（9），可以发现，贷款利率取决于无风险利率r、贷款期限T、公司价值波动率s以及公司贷款比率L四大因素。

我们可以通过典型数据测试一下这个利率模型的计算结果。例如，r = 4%，T = 5，= 26%。根据ZZ利率模型进行计算，当贷款作为公司负债占公司总价值的40%时，贷款利率精确到万分之一为4.44%。当贷款占公司总价值的50%、60%、70%、80%、90%时，贷款利率分别为4.93%、5.59%、6.38%、7.26%、8.21%。可见，随着公司贷款即负债比率的增加，违约风险逐渐增大，贷款利率也呈加速度地增加。

但是需要注意的是，上述计算未必正确。这样运用模型暗含了一个前提，即公司在获得该笔贷款前，债务比率为0%。但在现实中，公司往往是在有一定负债甚至有很高负债的情况下再申请贷款，也就是说，新贷款将使公司债务比率由原来的某个百分比增加到一个更高的百分比。比如，如果这笔贷款使企业的债务比率由原来的40%、50%、60%、70%、80%再增加10%，则贷款利率分别为6.89%、8.87%、11.10%、13.44%、15.78%。对照前面计算的5个百分比，显然，贷款利率大幅度提高了；而且贷款利率随负债率而加速度增加的程度也提高了。

由此可见，在模型正确的前提下，还需要对模型和现实的理解正确，对模型的应用正确，这样才会得到正确的计算结果。

四、ZZ模型与莫顿模型的相互印证

由于目前学术研究中“用数据说话”的盛行，许多学者通过某种方式得到金融模型后，往往习惯于用数据来“验证”，以表明自己模型的可靠。笔者认为，并非所有的模型都需要用数据来验证。这是因为，一是不同的“数据”之间会有矛盾，现实中的数据浩如烟海，究竟符合哪套数据的模型算是正确的呢？二是数据中既包含正确、也包含错误，既有阴错阳差，也有歪打正着。那么，什么模型需要靠数据来证明是正确的呢？不妨看一个模型，平均速度=距离/时间，这样的模型当然不需要数据验证，因为它有清晰严谨的逻辑支撑。相反，如果某套数据不符合这个模型，那一定说明数据（记录）有问题。这也就是说，严格符合逻辑的模型其实可以用来检验现实数据的合理性，而不是相反。

逻辑其实就是一种严格表达的道理。逻辑与数据的一个不同是，逻辑可以跨越时间和空间而保持有效。所以，在金融研究中，真正彻底的证明是两个符合逻辑的不同思路或方法得到同样的结论或模型。ZZ破产成本是基于严格逻辑推导出来的，从模型的形式到模型中包含的变量都是客观逻辑推导的结果，不受作者主观偏好的影响。同样，推导ZZ利率模型也是一个严格的逻辑过程，模型形式和变量都不是笔者主观选择的。在推理到最后一步之前，笔者也不知道利率模型的形式以及其中包含哪些变量。

在独立推导出ZZ利率模型之后，在搜索以往研究成果时，笔者发现，1974年，Merton同样运用严格的逻辑推导出了贷款风险补偿率模型3Merton, Robert C., On the Pricing of Corporate Debt: the Risk Structure of Interest Rates, Journal of Finance, 1974, 29: 449-470.，虽然思路和推理过程不同，但最后得到的模型形式和变量与ZZ贷款风险补偿率模型完全相同（只是各变量所用的符号不同）。Merton的贷款风险补偿率模型如下：

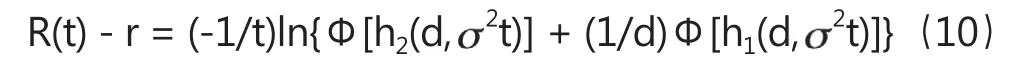
其中，R(t)为债券收益率，即银行贷款利率；r为无风险利率；t为债券（贷款）到期年限；ln{}为对数函数；Φ[]为标准正态分布的累积概率函数；h1(d,2t)和h2(d,2t)取值如下：

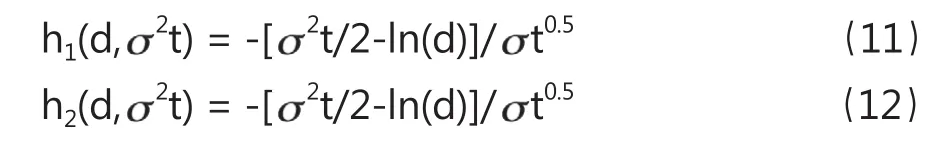
显然，按照Merton的利率模型，合理的利率取决于无风险利率r、贷款（贷款）年限t、公司风险即价值波动率以及公司负债率d，共4个变量。这与ZZ利率模型完全一致；同时，模型形式也是完全一致。相信读者自己可以辨认清楚。

当然，本文并不是重复Merton的研究，只是殊途同归，得到了与Merton一样的模型。先不说作为客观逻辑推理，不推导到最后其实不可能知道与Merton模型完全一致。但说Merton当年的推导，其过程要复杂难懂得多，可以说金融领域至今真正能看懂的人不在多数。事隔40年，本文经由不同的逻辑过程，基于ZZ破产成本模型，简单轻松推导出同样的模型。这有两个直接意义：其一，如上所述，它使Merton模型40年来第一次有了逻辑印证，从而可以坚定人们对Merton模型的信心；其二，金融领域有更多的人可以理解或看懂模型的推导过程，从而也才会更好地掌握和应用模型。从前面简单的计算演示中，读者已经看到，对模型掌握和应用的好与差，会导致计算结果大不相同。

五、有待进一步研究的问题

至此，本文拿出了一个贷款定价的基本模型。由于与Merton模型相互印证，从而模型的正确性得到了进一步的证实。限于篇幅，本文不做进一步的探讨，仅对有关问题做一些简单说明。

一个自然的思路是，既然已经建立模型，模型的正确性也得到某种证实，那顺理成章就应该探讨模型的应用了。但并不是任何正确的模型都值得探讨一下如何应用。比如，等同于常识的模型就不值得进一步探讨如何应用。因为直接按照常识决策就可以了，当然，Merton模型或ZZ利率模型显然不是常识。

那么，是不是正确的定量模型都值得探讨一下如何应用呢？也不是。举个例子，本文前面提到的Modigliani和Miller在1958发表的研究，后来被称为MM模型I，这是有关资本结构研究的第一个清晰的定量模型，同样也是经过严格逻辑推导建立的模型。模型的正确性也没有问题，后来Modigliani和Miller都因此获得诺贝尔经济学奖。但这个模型就不值得探讨如何应用。因为这个模型不是一个解决问题的模型，只是在解决问题的过程中的一个中间成果——当然是一个非常重要的成果。

所以，解决了相应决策问题的精确定量的模型才值得进行应用探讨。自然，接下来的问题就是：Merton模型或ZZ模型解决了贷款定价问题吗？

这看似是一个简单的问题，其实并不容易回答。究竟什么样的模型算是解决了问题，解决问题的标准是什么？在目前的金融领域，这种问题其实没有清晰的答案。当然，这个问题也没有难到无法回答的程度。我们有过很多次这方面的讨论，也得出了判断问题是否解决的标准。限于篇幅，这里不展开阐述了。根据我们的标准来判断，答案是肯定的，也就是说，Merton模型或ZZ模型解决了贷款定价问题；从而，可以在这个模型的基础上探讨模型在银行贷款实务中的应用了。