混洗蛙跳算法在农产品物流配送车辆路径上的应用

郑红剑++刘巧

摘要：针对当前农产品物流配送车辆路径问题中无法满足客户时间需求的问题，对混洗蛙跳算法进行改进，与带时间窗的车辆路径问题相结合进行分析研究，可以有效解决全局收敛和局部收敛问题。结果表明，G-SFLA算法是求解农产品物流配送车辆路径问题的较优方案。

关键词：混洗蛙跳算法；农产品物流；车辆路径问题

中图分类号：F274；C934 文献标识码：A 文章编号：0439-8114（2017）09-1755-04

DOI：10.14088/j.cnki.issn0439-8114.2017.09.039

Research of Agricultural Products Logistics Distribution Vehicle Routing Problem Based on Improved Algorithm of Shuffle Leap-frog

ZHENG Hong-jian，LIU Qiao

（Hubei Academy of Scientific and Technical Information，Wuhan 430074，China）

Abstract： According to current agricultural products logistics distribution vehicle routing problem， unable to meet needs of customers time， algorithm of shuffle leap frog combined with the vehicle routing problem with time Windows analysis was improved， which would solve the problem of global and local convergence， experiments showed that the G-SFLA algorithm for logistics distribution vehicle routing problem was an excellent plan.

Key words： shuffle leap frog algorithm；agricultural products logistics；vehicle routing problem

近年來，农产品电子商务发展迅速，已经在中国得到大力推广，农产品物流配送已经成为制约农产品电子商务发展的一个重要因素。中国农产品电子商务的发展竞争主要体现在农产品物流的配送方面，农产品车辆运输成本是物流企业首先考虑的问题。优化和改善物流配送过程，规划农产品物流配送的合理路径是提高物流企业利润和提升服务质量的关键。针对当前农产品物流配送车辆路径问题中无法满足客户时间需求的问题，本研究对混洗蛙跳算法进行改进，与带时间窗的车辆路径问题相结合进行分析研究，以期有效解决全局收敛和局部收敛的问题，为农产品物流配送发展提供参考[1]。

1 改进的多目标优化算法

1.1 混洗蛙跳算法原理

混洗蛙跳算法是一种基于启发式搜索的算法，2003年Eusuff、Lansay提出混洗蛙跳算法，通过启发函数进行搜索，最终找到最优解。该算法以模因算法为基础，结合粒子群优化算法而产生。

1989年Moscato提出模因算法（Memetic Algorithm，MA），Meme如同染色体上携带遗传信息的基因，只有被传播或重复的时候才可以称为Meme，该算法在处理局部问题时采用竞争与协作机制，解决其他算法无法解决的大型离散优化问题。

1995年Eberhart和Mennedy根据鸟群捕食的行为模拟简化的社会模型提出粒子群优化算法。其原理是在D维搜索空间以特定速度运动着的粒子群体里，每个粒子不断地搜索相关范围内其他粒子的相优值，并在此基础上进行位置变化。粒子的速度和位置公式如下：

V ■■=V ■■+c1ξ（P ■■-x ■■）+c2η（P ■■-x ■■） （1）

V ■■=V ■■+V ■■ （2）

其中，C1、C2为学习因子，具有学习和自我总结的能力，使粒子不断地向历史最优点逼近；ξ，η∈[0，1]，是区间内的一个均匀分布随机数，xi=（xi1，xi2，…，xiD）为第i个粒子位置，pi=（pi1，pi2，…，piD）为粒子经历过的历史最好点，pg=（pg1，pg2，…，pgD）为粒子经过的历史最好点。

1998年Shi和Eberhart在算法中引入惯性权重，改善了算法的收敛性能，将速度公式（1）改为：

V ■■=ωV ■■+c1ξ（P ■■-x ■■）+c2η（P ■■-x ■■） （3）

其中ω为惯性权重，其值的大小可以使粒子具有均衡的探索能力和开发能力。当ω=1时，就是标准的基本粒子群优化算法。

混洗蛙跳算法通过模拟自然界中大量青蛙集体觅食生成的一种群体协同搜索算法，利用个体及群体间信息的传递，将全局信息交换和局部搜索有效地结合。将空间中的青蛙划分为若干个子群体，各个子群体都有其自身的特性，子群中的每个青蛙也有个自特性并对其他个体产生影响，随着蛙群的进化也发生改变，当这些子种群进化到一定程度时，将这些子种群进行混合，实现信息的交流，直到满足终止条件[2]。该算法将局部深度搜索与全局交换搜索相结合，摆脱了陷入局部最优的现象。

1.2 算法流程

步骤1：种群初始化，求解空间中，种群F包含m（m=z×n）只青蛙。其中z表示整个种群划为分子种群的数量，n为每个子种群中包含的青蛙数量。维数为d，每个青蛙的位置表示一个候选解，第i只青蛙的位置F（i）的适应值用fi表示。

步骤2：种群中的所有青蛙根据个体适应值的大小按降序排序，生成组数X={F（i），fi；i=1，2，…，m}，当i=1时，表示该青蛙的位置最好。

步骤3：对整个种群按m=z×n分为z个组群Y1，Y2，…，Yz，即：

Yk={F（j），fj|（j）=F[k+z（j-1）]，fj=[k+z（j-1）]，j=1，2，3…，n}，将第1只青蛙分入Y1子群，第2只青蛙分入Y2，以此类推，第z只青蛙分入Yz，第z+1只青蛙分为Y1，直至所有青蛙都分配完为止。

步骤4：在每个子种群memeplex中，每个青蛙都受到其他青蛙的影响，不断地向目标接近。采用的进化流程如下：

1）初始化迭代次数dN=0，通过每次进化，青蛙个体之间的信息交流，对最坏位置青蛙的位置进行改善。

2）dN=dN+1。

3）对青蛙的位置进行移动，每次青蛙移动的距离不能超过可移动的最大距离。

4）对每次青蛙的新位置与原位置相比较，其优于原位置，用新位置上的青蛙代替原来的青蛙，否则用历史最好点的青蛙pg代替子种群中位置最好的青蛙pb，不断重复上述动作。

5）若上述操作不能产生新解，那么就随机产生一个新的位置代替该子种群中位置最差的青蛙pw。

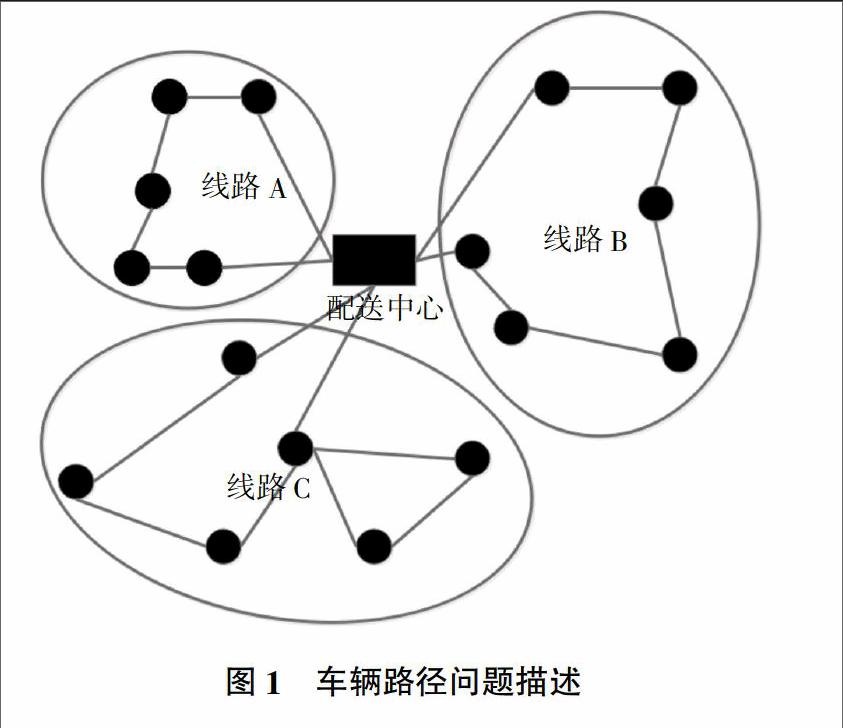
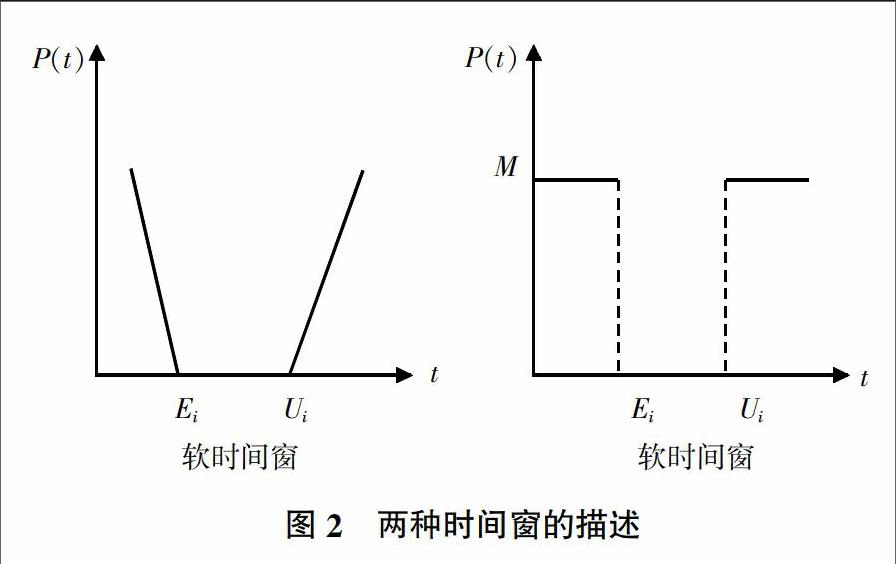
6）若dN

步骤5：青蛙经过memetic进化后，将其子种群进行混合，重新按适应值进行排序。

步骤6：满足结束条件，直接结束，否则跳至步骤3。

1.3 改进的混洗蛙跳算法

混洗蛙跳算法在全局搜索能力上比较强，但假如问题比较复杂时，则存在收敛速度慢和易陷入局部极值的问题，将遗传算法引入到混洗蛙跳算法中可以在保持原算法优点的基础上，具有跳出局部最优的能力，即遗传混洗蛙跳算法（Genetic-Shuffle Flog Leaping Algorithm，G-SFLA）。

G-SFLA与SFLA的不同点是对分组进化采取遗传算法的交叉和变异运算，这两个运算应用在流程的步骤4中。交叉运算指的是随机将性能最好的青蛙Pb与性能最差的青蛙Pw的相同位置设为交叉点，将这两个个体的交叉点右边交换，生成两个新解。若产生的新解位置优于Pw，则代替Pw。若产生的新解不优于Pw，则随机对Pw的若干位进行变异运算，从而产生新解代替原来的Pw。

G-SFLA中，对于分组也进行了一定的改进，对于SFLA的分组方法，最后一组的个体在整个群体中相对适应值比较差的个体，即使该组成员不断经过信息交流和学习，也无法得到一个较好的进化结果。由于分组的不均匀，使学习的局限性放大。新的分组方式是在原来分组的基础上，随机从其他组中抽出若干个体加入了该组中，此时组成员的个数变为n+z-1，小组的多样性得到了认同，发挥了遗传运算的优势。需要注意的是，当小组重新合并为一个种群时，种群中个体的数量增加了z×（z-1）个，重新对所有的个体进行排序，删除重复的个体。删除后的个体数量大于z，则取前z个个体进行下一轮的迭代，假如不足z个个体，随机产生个体，补足z个进行下一轮迭代。

2 车辆路径问题

2.1 车辆路径问题的描述

近年来，中国的物流行业发展迅速，但是农产品物流的配送模式相对比较落后，无形之中增加了运营的成本。对于物流企业来说，物流车辆的调度问题是最关键的，利用信息技术和数学知识对农产品车辆路径问题建立模型，通过模型分析农产品车辆的运输能力，可以为物流企业节约大量的成本。

农产品车辆路径问题是指对一系列的发货点和收货点规划合适的行车路线，在一定的约束条件（需求量、发货时间、发货量、车辆容量限制、时间限制及行驶距离限制等）下，让车辆有序地通过各个节点，达到使用车辆最少、行驶距离最短和花费最少的目标。车辆路径问题简称VRP，在1959年由Ramser 和Dantzig提出，隨着社会经济的不断发展，很快受到计算机学科和数学相关学科的重视[3]。VRP可以描述如图1所示。

以配送中心为中心，形成若干个客户群体，即多个配送路线，每个线段代表着运输的费用，在建立配送线路时，一般目标函数设计为以下两种：

1）客户满意度（客户对配送时间的要求）。

2）企业运营成本最小（车辆使用成本、运输成本、企业配送时间成本等）。

对于VRP的约束条件主要有车辆运行时间、配送中心的开放时间、车载容量、最大车辆数等。

2.2 带时间窗的车辆路径问题

随着物流行业的不断发展，客户对送货时间的满意度成为物流行业之间竞争的主要因素，将客户的时间窗这一限制与车辆路线优化相结合形成带时间窗的车辆路径问题（VRPTW）。VRPTW除了考虑企业的运营成本之外，还考虑到客户在等待物流车辆时所占用的时间。将带时间窗的车辆路径问题描述如下：一个配送中心、M辆一定载重的农产品运输车辆和N个客户节点[4]。其中已知条件为配送中心及客户节点的位置，运输车辆的载重量、每个客户的需求量及第i个客户允许等待服务的时间[Ei，Ui]，车辆路径问题的目标是设计出合理的行驶路线，使得客户等待的时间最短，达到最高的满意度。

对于时间窗的设置主要有三种，一种是硬时间窗，即要求配送车辆必须严格按照要求时间送达，早到则等待客户，迟到则客户拒收；第二种是软时间窗，在规定的时间窗内没有配送到达，无论是早到或迟到，都要受到处罚，该处罚不同于硬时间窗的等待与拒收，早到或迟到的时间越久，所受到的处罚越严重。描述两种时间窗如图2所示。

3 G-SFLA在农产品物流配送VRP中的应用

3.1 带时间窗的VRP数学模型

带时间窗的VRP的相关描述如下：一个配送中心用0表示，配送中心可以有M辆车与N个客户，一辆配送车辆的最大行驶距离为D，一辆车的载重为Q，设置配送中心的坐标位置为（X0，y0），第i个客户的坐标为（xi，yi），第i个客户接收配送物品的时间窗为[e，u]，需求量为qi，每个车辆到达第i个客户位置后的时间为ti，给客户服务的时间为si，从第i个客户到第j个客户所需的时间为tij，两个客户之间的距离为dij，当第m辆车为第i个客户服务后行驶至第j个客户为其服务为决策变量Xijm，Xijm只能为1或0。配送车辆只为每个客户服务一次，规划出合理的农产品配送车辆行驶路线，使得企业的运营成本最低，客户的满意度最高[5，6]。建立的数学模型如下：

MinA1=∑■■∑■■∑■■Xijm （4）

该公式为目标函数1，表示配送车辆行驶的距离最小。

MinA2=∑■■∑■■{max（ei-tim）+max（tim-ui）} （5）

该公式为目标函数2，表示配送车辆行驶的等待时间及迟到时间花费的最少，即车辆准时到达的次数最多。除了目标函数外，还有约束函数，主要是每个客户都必须得到服务且只能由一辆配送车辆提供，配送中心发出的车辆不能超过总车辆M。

3.2 G-SFLA求解模型的算法设计

根据G-SFLA算法的流程，算法的设计主要有编码、种群初始化、适应值排序、分配组群、进化（交叉和变异运算）等五个方面[7]。

1）编码。根据数学模型，将配送中心设置为0，N个客户从1至N进行表示，则最多有N条路线，N条路线与N个客户结点相结合，形成2N个自然数序列。每个客户和线路都只能执行一次，是算法的一个基本约束条件。

2）种群初始化。在求解空间中，种群F包含n个客户和n条线路。假设一辆配送车辆可以包含一个组群，则m辆车表示整个种群划分子种群的数量，每个客户的位置表示一个候选解，第i个客户的位置F（i）的适应值用fi表示。

3）适应值排序。对每个客户的适应值按大小进行排序，排序由目标函数和约束函数的评估结果来决定，先利用约束条件对其进行初步的筛选。

4）分配组群。与适应值相近的客户分配为一个组群，由一辆配送车辆来完成配送。初步分配的组群中客户的数量是相同的，即n/m。

5）进化。进化操作利用交叉和变异两种运算，使算法实现全局收敛和局部收敛。其中交叉运算指的是随机将计算出性能最好的客户适应值Pb与性能最差的客户Pw的相同位置设为交叉点，将这两个客户的交叉点进行右边交换，生成两个新解。若产生的新解位置优于Pw，则代替Pw。若产生的新解不优于Pw，则随机对Pw的若干位进行变异运算，从而产生新解代替原来的Pw。在不断的迭代过程中，不断地划分每辆配送车辆的行驶范围，即不断规划出新的行驶路线，最终达到最优。

4 小结

针对时间窗的车辆路径问题的算法分析，有效地解决了农产品运输车辆路径优化问题，可以为物流配送企业的决策者提供配送方案的最优解。但是，本研究的算法是建立在一种相对理想的状态，如给每个客户的服务时间是相同的，这在现实中是不可能的，另外随着客户量的不断增加，算法能否适应未来发展的需要，也是需要进一步研究。

参考文献：

[1] ZITZLER E，THIELE L.Multiobjective evolutionary algorithms：A comparative case study and the strength pareto approach[J].IEEE Transactions on Evolulionary Compution，1999，3（4）：257-271.

[2] DNATZIG G，RAMSER J. The truck dispatching porblem[J]. Management Science，1959（6）：80-91.

[3] 劉云忠，宣慧玉.车辆路径问题的模型及算法研究综述[J].管理工程学报，2005，9（1）：124-131.

[4] EUSUFF M，LANSEY K E. Optimization of water distribution network design using the shuffled frog leaping algorithm[J]. Water Resources Planning and Management，2003，129（3）：210-225.

[5] 染垚深，盛建伦.基于粒子群算法的混洗蛙跳算法[J].计算机与现代化，2009（11）：39-41.

[6] ZHEN Z Y，WANG D B，LIU Y Y. Improved shuffled frog leaping algorithm for continuous optimization problem[C].USA：IEEE Congress on Evolutionary Computation，2009.

[7] 尚荣华，焦李成，马文萍，等.用于约束多目标优化的免疫记忆克隆算法[J].电子学报，2009，37（6）：1289-1294.