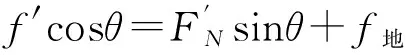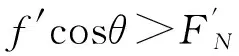例说斜面上的力学问题

成金德

(浙江省义乌市第二中学，浙江 义乌 322000)



例说斜面上的力学问题

成金德

(浙江省义乌市第二中学，浙江 义乌 322000)

斜面上的力学问题是力学中的一类典型问题,在考试中会经常看到它们的身影．本文探究此类问题的解题方法，以期对习题教学有一定参考作用.

斜面体；模型；牛顿运动定律

斜面上的力学问题是力学中的一类典型问题,在考试中会经常看到它们的身影．在物理教学中,学生遇到此类问题常常望而生畏、望而却步．如何解答此类问题,往往成为力学中的一个重要问题,本文就此进行一些探讨．

模型1.斜面上的滑块处于静止状态.

解题的关键是把握3个要点: (1) 滑块在斜面上静止时,滑块所受的支持力和摩擦力的合力与重力是一对平衡力．(2) 对斜面体所受地面的摩擦力一般取整体法研究．(3) 灵活应用平衡条件．

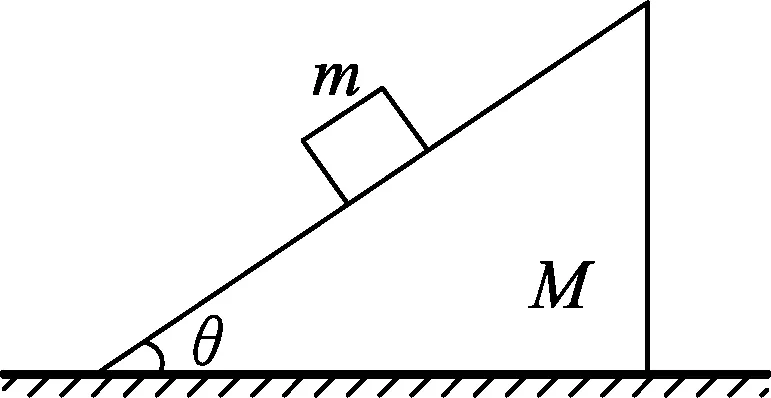
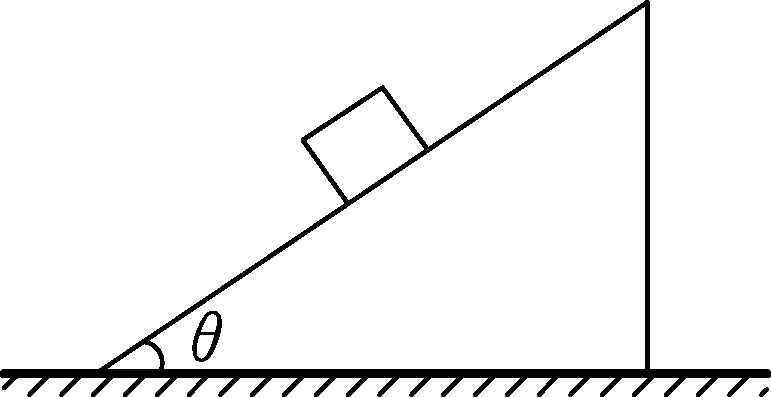
图1

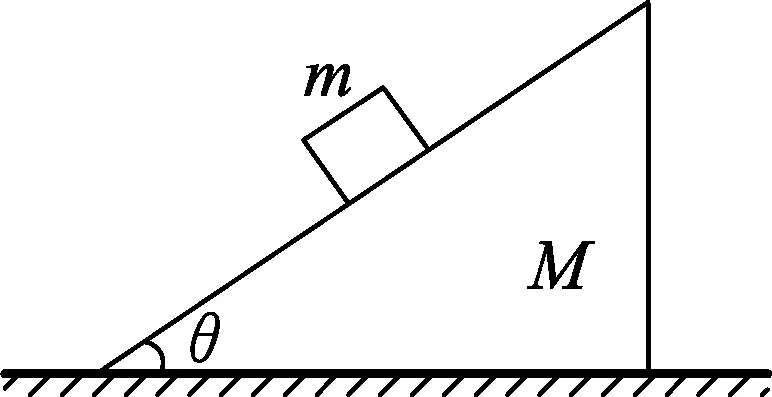
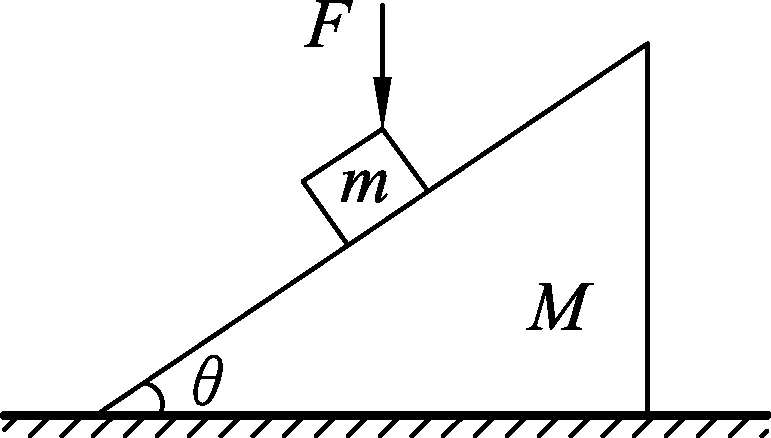
例1.质量为M的斜面体静止在水平地面上,斜面的倾角为θ,质量为m的滑块恰好静止在斜面体上,如图1所示．则

(A) 滑块所受的摩擦力大小为mgsinθ.

(B) 滑块对斜面的压力大小为mgcosθ.

(C) 斜面体所受地面的摩擦力大小为mgsinθ.

(D) 滑块所受合外力等于0.

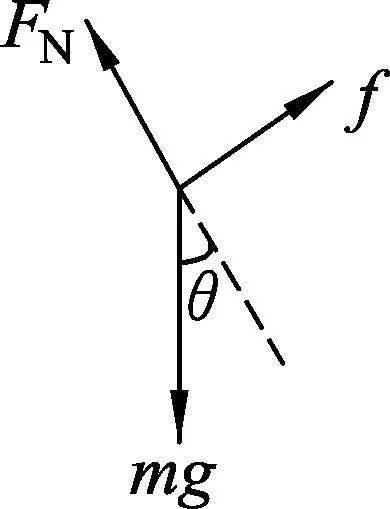
解析:滑块受重力mg、支持力FN和摩擦力f的作用．由平衡条件可求得滑块所受摩擦力的大小与重力沿斜面方向的分力的大小相等,即f=mgsinθ,则选项(A)正确;滑块对斜面体的压力大小与斜面体对滑块的支持力大小相等,而斜面体对滑块的支持力的大小等于重力沿垂直于斜面方向分力的大小,即FN=mgcosθ,可见选项(B)正确;由于滑块处于静止状态,因此,滑块所受的合力等于0,选项(D)正确;取斜面体和滑块这个整体为研究对象,整体除了受到重力和地面的支持力外,若地面对斜面体有摩擦力的作用,则整体不可能处于平衡状态,因此,选项(C)错误．

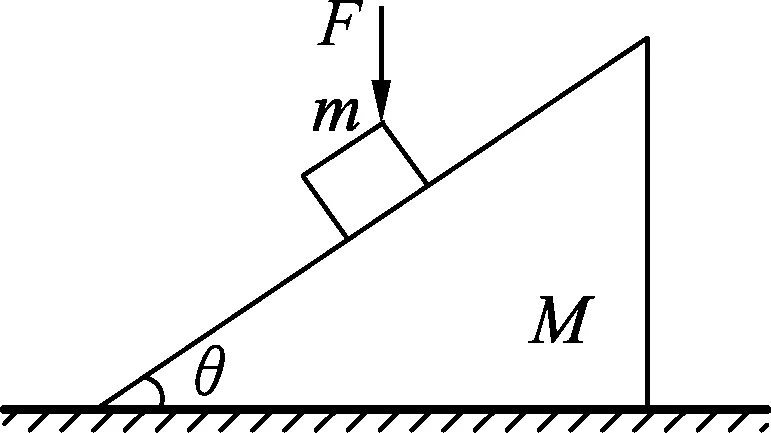
图2

变式1.一质量为m的滑块恰好静止在倾角为θ的斜面体上．现对滑块施加一个竖直向下的恒力F,如图2所示．则滑块

(A) 仍处于静止状态.

(B) 沿斜面加速下滑.

(C) 受到的摩擦力不变.

(D) 受到的合外力增大.

解析:滑块静止在斜面体上,沿斜面方向,滑块重力的分力与摩擦力大小相等,设想摩擦力是最大静摩擦力,即mgsinθ=μmgcosθ．当在滑块上加一竖直向下的力F时,可将F与重力合并,显然关系式mgsinθ+F=μ(mg+F)cosθ依然成立,说明滑块仍然处于静止状态．当加上F后,滑块受到的沿斜面向下的分力增大,则受到的摩擦力必增大,所以,只有选项(A)正确．

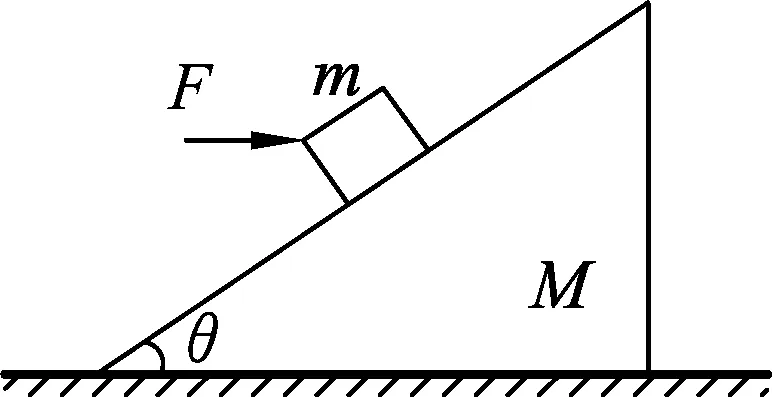
图3

变式2.如图3所示,质量为m的滑块在水平恒力F作用下静止在斜面体上,斜面体静止在水平桌面上,倾角为θ,质量为M．下列说法正确的是

(A) 滑块受到的摩擦力方向沿斜面向下.

(B) 滑块对斜面体的压力大小是mgcosθ.

(C) 桌面对斜面体的摩擦力大小是0.

(D) 桌面对斜面体的支持力大小是(m+M)g.

解析:由于F大小不确定,则滑块摩擦力可能沿斜面向上也可能沿斜面向下,选项(A)错误;滑块对斜面体的压力大小为Fsinθ+mgcosθ,因此选项(B)错误;以整体为研究对象,水平方向所受的合力应等于0,则桌面对斜面体的摩擦力大小等于F,即选项(C)错误;竖直方向上,桌面对斜面体的支持力大小等于(mg+Mg),可见选项(D)正确．

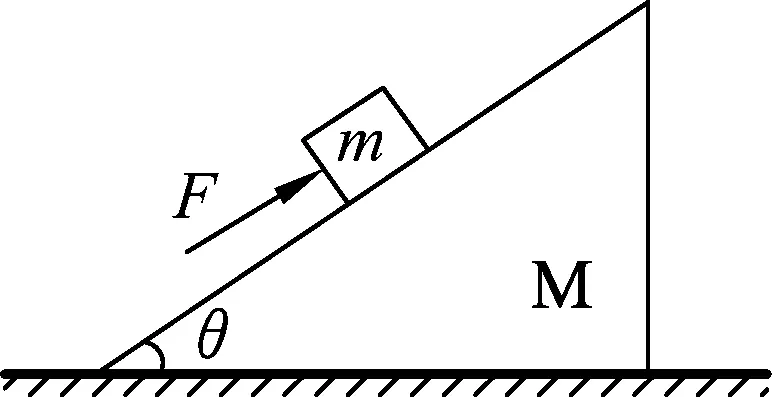
图4

变式3.如图4所示,位于斜面体上的滑块m在沿斜面向上的力F作用下,处于静止状态．则斜面体作用于滑块的静摩擦力的

(A) 方向可能沿斜面向上.

(B)方向可能沿斜面向下.

(C) 大小可能等于0.

(D) 大小可能等于F.

模型2.斜面上的滑块处于匀速状态.

与模型1相似,应抓住3点: (1) 滑块在斜面上匀速运动时,滑块所受的支持力和摩擦力的合力与重力是一对平衡力．(2) 对斜面体所受地面的摩擦力一般取整体法研究．(3) 灵活应用平衡条件．所不同的是受到的摩擦力是滑动摩擦力,应注意区分．

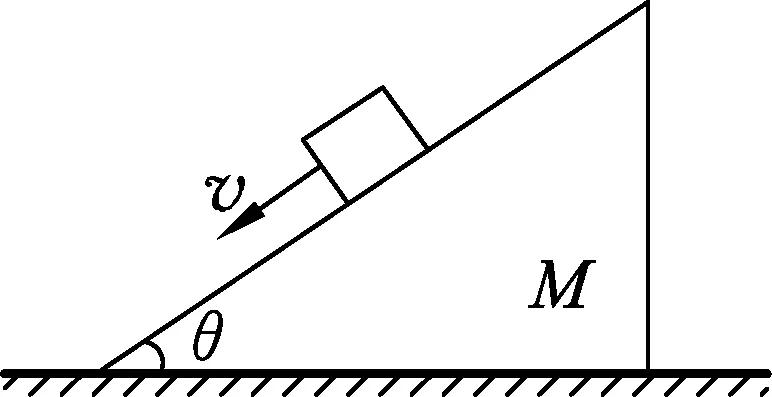
图5

例2.如图5所示,粗糙的水平地面上有一斜面体,斜面体上一滑块正在沿斜面以速度v匀速下滑,斜面体保持静止,则地面对斜面体的摩擦力

(A) 等于0.

(B) 不为0,方向向右.

(C) 不为0,方向向左.

(D) 不为0,速度较大时向左,速度较小时向右.

解析:当斜面体上的滑块匀速下滑时,滑块受重力、斜面体给的支持力和摩擦力的作用,其中斜面体给的支持力和摩擦力的合力与重力是一对平衡力,因此,滑块对斜面体的作用力方向竖直向下,斜面体对地面无相对运动趋势,则无静摩擦力的作用．另外,从整体上看,斜面体在水平方向也不可能受到静摩擦力的作用,否则,整体在水平方向不可能处于平衡状态,故选项(A)正确．

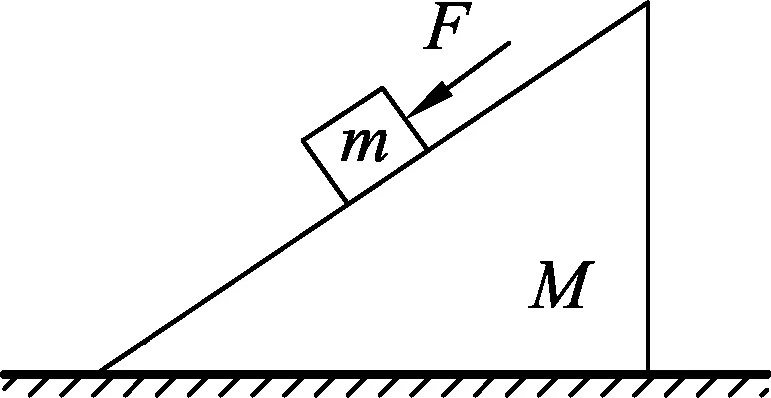
图6

变式1.如图6所示,质量为M的斜面体静止在粗糙的水平地面上,一质量为m的滑块恰能沿斜面匀速下滑．现施加一沿斜面向下的推力F作用于滑块,使滑块沿斜面匀加速下滑,此过程中,关于斜面与水平面间相互作用力的说法正确的是

(A) 有摩擦力作用,对水平面的压力等于(M+m)g.

(B) 有摩擦力作用,对水平面的压力大于(M+m)g.

(C) 无摩擦力作用,对水平面的压力等于(M+m)g.

(D) 无摩擦力作用,对水平面的压力大于(M+m)g.

解析:力F的作用对物体给斜面的压力和摩擦力没有影响,故斜面与水平面间无摩擦力作用,斜面对水平面的压力大小不变．故选项(C)正确．

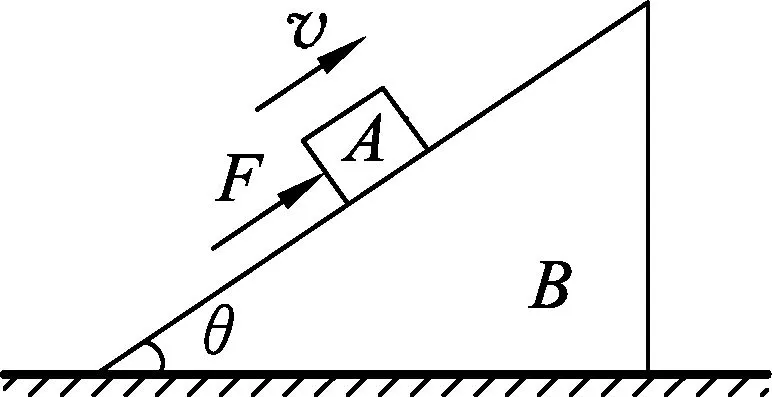
图7

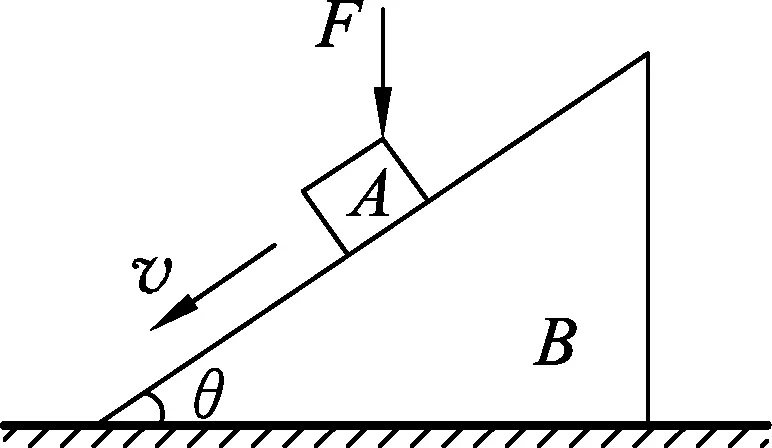
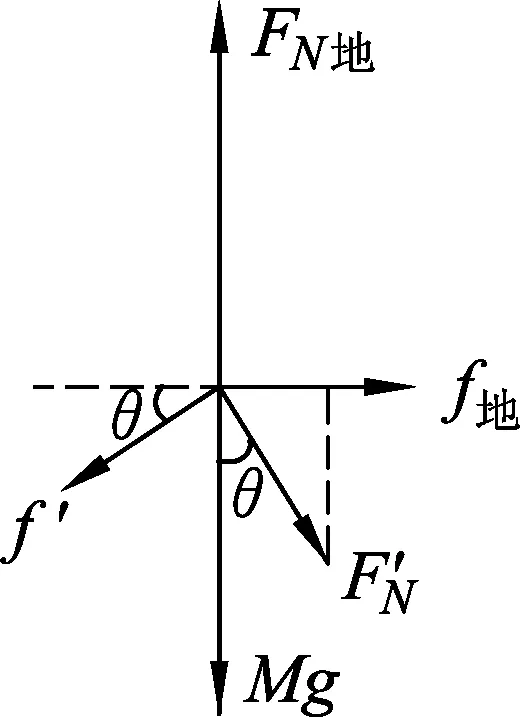
变式2.如图7所示,一质量为M的斜面体B放在水平面上,在斜面上放一质量为m的滑块A,用一沿斜面向上的力F作用于A上,使其沿斜面匀速上滑,在A上滑的过程中斜面体B相对地面始终静止,则关于地面对斜面体的摩擦力f及支持力FN的说法正确的是

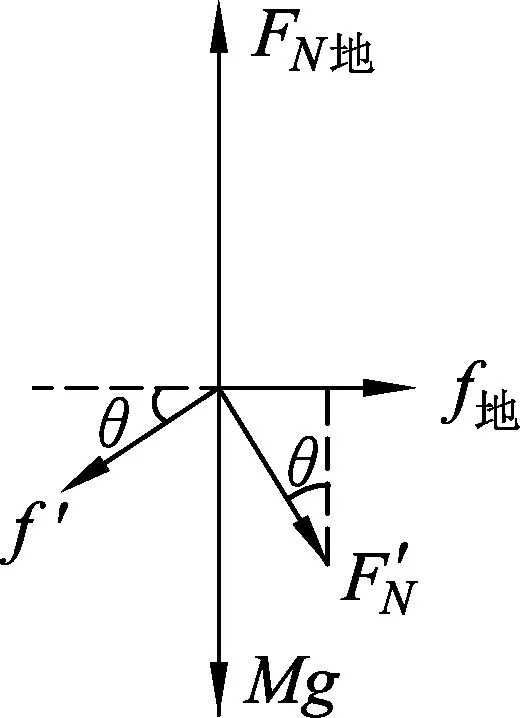
(A)f=0,FN=Mg+mg.

(B)f向左,FN=Mg+mg.

(C)f向右,FN

(D)f向左,FN

解析:由于F沿斜面体向上方向,则A对B的摩擦力方向为沿斜面体向上方向,A对B的压力和摩擦力的合力方向不再沿竖直向下方向,斜面体将受到地面的摩擦力作用．取整体为研究对象,由于F的作用,使得斜面体受到地面的摩擦力作用,摩擦力的方向水平向左．又由于F有一沿竖直方向的分力,则斜面体受到地面的支持力小于斜面体和滑块的重力,可见选项(D)正确．

图8

变式3.如图8所示,一质量为m的滑块恰能在一个质量为M的斜面体上沿斜面匀速下滑．现用一与斜面成α角的推力推此滑块,使滑块沿斜面加速下滑,则关于斜面受到地面的摩擦力f和支持力FN的说法正确的是

(A) 摩擦力f为0.

(B) 摩擦力f方向向左.

(C) 支持力FN=(M+m)g.

(D) 支持力FN>(M+m)g.

解析:将F分解为沿斜面体方向和竖直向下的两个分力的作用,而竖直方向和沿斜面体方向的力,不影响地面对斜面体的摩擦力,即斜面体不受地面的摩擦力作用,则选项(A)正确．但竖直方向的分力将影响地面对斜面体的支持力,即选项(D)正确．

变式4.如图9(a)所示,质量为M的斜面体B放在水平面上,在斜面体的斜面上放一个质量为m的滑块A,用一个竖直向下的力F作用于A上,滑块A刚好沿斜面匀速下滑．若改用一个斜向下的力F′作用在A时,滑块A加速下滑,如图9(b)所示,则在图9(b)中关于地面对斜面体的摩擦力f地及支持力FN地的结论正确的是

(A)f地=0,FN地>Mg.

(B)f地=0,FN地

(C)f地向右,FN地

(D)f地向左,FN地>Mg.

解析:设斜面的倾角为θ．在图9(a)中,滑块A受力情况如图9(c)所示．由平衡条件可得

(mg+F)sinθ=μ(mg+F)cosθ，

解得μ=tanθ.

(a)

(b)

(c)

(d)

在图9(b)中,斜面体B的受力情况如图9(d)所示．设地面对斜面体B的摩擦力方向为水平向右,由平衡条件在水平方向有

f地=fcosθ-FNsinθ，

又因为f=μFN，解得

f地=μFNcosθ-FNsinθ=tanθFNcosθ-FNsinθ=0．

在竖直方向有FN地>Mg．可见选项(A)正确．

模型3. 斜面上的滑块处于加速状态.

解题的关键应把握以下2点: (1) 对加速运动,应灵活运用牛顿第二定律建立方程．(2) 对斜面所受到地面的摩擦力和地面的支持力,一般应用整体法分析．

图10

例3.如图10所示,倾角为θ的斜面体,质量为M,静止放在粗糙的水平地面上．质量为m的滑块沿斜面由静止开始加速滑下．已知接触面均粗糙,动摩擦因数为μ,且在滑块加速下滑过程中斜面体始终保持静止,则

(A) 滑块对斜面体的压力为mgsinθ.

(B) 滑块沿斜面下滑的加速度为gsinθ.

(C) 斜面体对地面的压力大于(m+M)g.

(D) 斜面体受到地面的静摩擦力方向水平向左.

解析:斜面上的滑块对斜面的压力大小等于滑块的重力沿垂直于斜面方向的分力,即F=mgcosθ,选项(A)错误;对滑块应用牛顿第二定律得mgsinθ-μmgcosθ=ma,求得滑块的加速度为a=gsinθ-μgcosθ,可见,选项(B)错误;对整体在竖直方向应用牛顿第二定律得(m+M)g-FN=may,可见,选项(C)错误;对整体在水平方向应用牛顿第二定律得f=max,所以,斜面体受到静摩擦力方向水平向左,则选项(D)正确．

图11

变式1.质量为M=20kg的楔形斜面体静置在粗糙的水平面上,斜面体的倾角θ=30°．有一质量m=1.0kg的滑块由静止开始沿斜面下滑,当滑块滑行的距离x=2.8m时,滑块的速度v=2.8m/s,在这一过程中斜面体保持静止不动,重力加速度取g=10m/s2．求:

(1) 滑块下滑过程中,地面对斜面体的摩擦力的大小和方向．

(2) 滑块下滑过程中,地面对斜面体的支持力的大小．

解析:滑块滑行的加速度为v2=2ax,即

取整体为研究对象,在水平方向,只受到地面对斜面体的摩擦力作用,根据牛顿第二定律得

f=max,

即f=macos37°=1.12N,方向水平向左．

在竖直方向,整体受到重力和地面给的支持力,由牛顿第二定律得

(m+M)g-F=may,即F=(m+M)g-may=209.16N,方向竖直向上．

图12

变式2.如图12所示,放在固定斜面体上的滑块以加速度a沿斜面匀加速下滑,若在物块上再施加一个竖直向下的恒力F,则滑块

(A) 可能匀速下滑.

(B) 仍以加速度a匀加速下滑.

(C) 将以大于a的加速度匀加速下滑.

(D) 将以小于a的加速度匀加速下滑.

解析:当滑块沿斜面匀加速下滑时,设滑块与斜面间的动摩擦因数为μ,根据牛顿第二定律得

mgsinθ-μmgcosθ=ma.

当在滑块上施加一个竖直向下的恒力F时,将F和重力mg合并,根据牛顿第二定律得

(mg+F)sinθ-μ(mg+F)cosθ=ma1.

比较两式可知,a1>a,因此,选项(C)正确．

图13

变式3.如图13所示,质量为M的斜面体静止在粗糙的水平地面上,一质量为m的滑块沿斜面匀加速下滑,斜面体对地面压力为F1;在滑块上施加一沿斜面向下的推力F,在物块沿斜面下滑的过程中,斜面体对地面压力为F2.则

(A)F2>(M+m)g,F2>F1.

(B)F2>(M+m)g,F2=F1.

(C)F2<(M+m)g,F2>F1.

(D)F2<(M+m)g,F2=F1.

解析:当不加推力时,对滑块应用牛顿第二定律可得

mgsinθ-f=ma1.

(1)

将加速度沿水平和竖直方向分解,则竖直方向的加速度为

ay=a1sinθ.

(2)

对整体在竖直方向应用牛顿第二定律得

Mg+mg-F1=may.

(3)

联立以上(1)～(3)式得

F1=Mg+mg-may=Mg+mg-(mgsinθ-f)sinθ.

当加推力F后,对滑块m应用牛顿第二定律得

F+mgsinθ-f=ma2.

(4)

加速度的竖直分量为

ay2=a2sinθ.

(5)

对整体在竖直方向应用牛顿第二定律得

Mg+mg+Fsinθ-F2=may2.

(6)

联立以上(4)～(6)式得

F2=Mg+mg-(mgsinθ-f)sinθ.

比较后可知，F1=F2<(M+m)g．故选项(D)正确．

模型4.斜面上的物体受到几个力作用.

解答受到多个力的斜面问题,关键是抓住两点:(1) 灵活应用隔离法和整体法;(2) 灵活应用平衡条件和牛顿运动定律．

图14

例4.如图14所示,斜面体A静止放置在水平地面上,质量为m的滑块B在外力F1和F2的共同作用下沿斜面体表面向下运动．当F1方向水平向右,F2方向沿斜面体的表面向下时,斜面体受到地面的摩擦力方向向右．则下列说法中正确的是

(A) 若同时撤去F1和F2,在滑块B仍向下运动的过程中,滑块B的加速度方向一定沿斜面向上.

(B) 若只撤去F1,在滑块B仍向下运动的过程中,A所受地面摩擦力的方向可能向左.

(C) 若只撤去F2,在滑块B仍向下运动的过程中,A所受地面摩擦力的方向一定向右.

(D) 若只撤去F1,在滑块B仍向下运动的过程中,A所受地面摩擦力不变.

解析:取斜面体A为研究对象,受力情况如图15(a)所示,由题意知,斜面体受到地面的摩擦力方向向右,则B对A一定有滑动摩擦力,且方向沿斜面向下．设斜面倾角为θ,A、B间的动摩擦因数为μ．由平衡条件得

(a)

(b)

(1)

μcosθ>sinα.

(2)

若同时撤去F1和F2,在滑块B仍向下运动的过程中,B受力情况如图15(b)所示,则

f=μFN=μmgcosθ>mgsinθ.

可见,滑块B所受的合力方向沿斜面向上,则滑块B的加速度方向一定沿斜面向上,则选项(A)正确．

总之,解决斜面上的力学问题,关键是抓住斜面上的力学特征,灵活运用平衡条件和牛顿运动定律,巧妙选用隔离法和整体法．

1 成金德.突破解动力学问题思维障碍的方法[J]. 考试,2000(04)：43-45.

2 成金德.应用牛顿第二定律解题的类型和方法[J]. 中学生理科应试,2002(08)：21-23.

2016-12-07)