数学开放性问题探讨

刘仁道

[摘要]数学开放性问题是相对于传统的“条件完备，结论确定”的封闭性问题而言的，这类问题可能所提供的条件不完备，需要在求解过程中不断充实和增添假设，也可能是结论或结果多样化，解决开放性问题的思路和途径是因人而异，灵活多样的。

[关键词]开放性问题平行四边形判定定理

[中图分类号]G633.6

[文献标识码]A

[文章编号]1674-6058（2016）32-0061

在国培网络学习中，有一节课我印象特别深刻，那就是《平行四边形的判定》第二节课，那节课主要是在讲了平行四边形的判定定理1和判定定理2后，讲解判定定理3和判定定理4，教者通过复习回顾，引导学生从平行四边形的对角线、角应具备的特征对平行四边形的判定方法进行猜想、验证，从而发现新知，为此，教者设计了两个问题：（1）上节课中对平行四边形的判定定理1的研究是怎样引入的？它和性质有怎样的关系？（2）你认为还可以从哪些方面研究平行四边形的判定方法？怎样证明你的猜想？

在新知识巩固与应用阶段，教者精心设计了三个递进的材料组合式的开放性问题，下面就探讨一下这几个开放性问题。

[变式1]已知在平行四边形ABCD中，E，F是对角线BD上的两点，如果BE=DF，那么四边形AECF是平行四边形吗？

从上例的证明中可以知道，有不同的证明方法判断四边形AECF是平行四边形，这是一题多解的问题，目的是想让学生在解决问题的过程中，进一步熟悉平行四边形的5种判定方法以及每种方法所需的两个条件，并学会对各种不同的证明方法进行比较和评价，体会应用判定定理3证明本题的优越性，设计开放性问题，不但能帮助学生巩固知识与技能，而且能渗透优化思想，提高学生的解题能力。

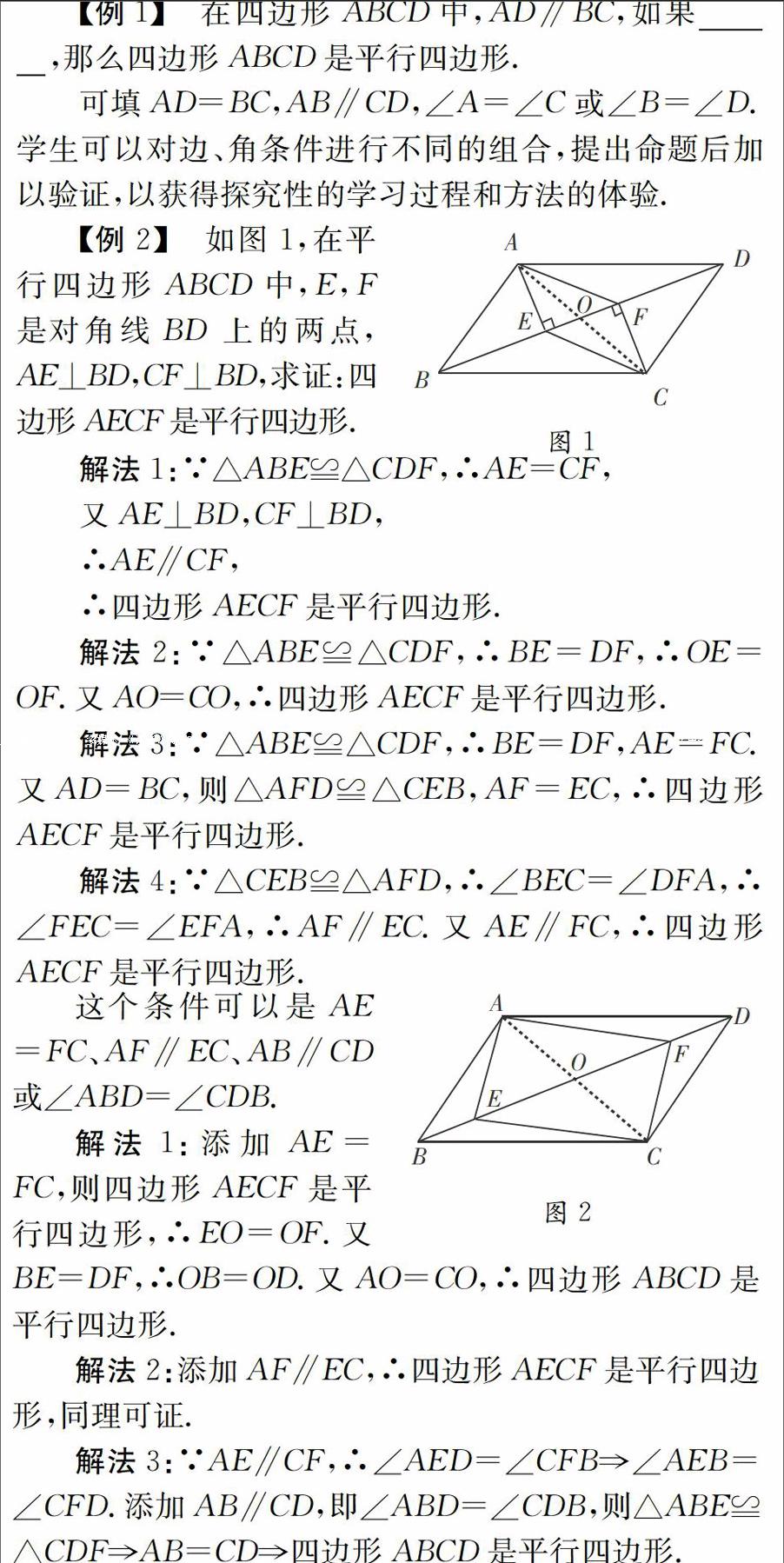
[变式2]如图2，已知在四边形ABCD中，E，F是对角线BD上的两点，如果BE=DF，AE∥CF，那么要使四边形ABCD是平行四边形，还需添加一个条件，这个条件可以是___。

设计开放性问题的目的是想让学生通过解决开放性问题，能进一步理解、巩固判定一个四边形是平行四边形所需的条件，同时发展学生的思维，培养学生的创新意识和能力，开放性问题可以激励学生主动参与，增强学生的学习自信心，有助于培养学生良好的思维品质。

设置开放性问题要注意以下几点：第一，设计的问题要能够引导学生从不同的角度对问题进行思考，形成不同的解题思路，甚至引起学生的争论；第二，在原题的基础上适当改变条件，引导学生从已知的开放性问题出发进行引申、推论，从而激发学生的探索兴趣；第三，合理地处理现有教科书中的问题，将封闭性问题改为开放性问题，改变设问方式，更换题设条件，互换条件结论，综合拓展类比等，相信教師不断向这个方向努力，教学水平定会得到不断提高。