基于假设检验的回归模型算法在脱靶量解算中的应用

姚尚杨博 胡长城 雷蕾 李斌

（甘肃酒泉十四支局565号，酒泉 735018）

基于假设检验的回归模型算法在脱靶量解算中的应用

姚尚†杨博 胡长城 雷蕾 李斌

（甘肃酒泉十四支局565号，酒泉 735018）

在脱靶量处理中，准确选取弹道的拟合函数是计算脱靶参数的关键.本文首先利用假设检验的回归模型算法，合理选取模型并确定函数阶次，提高函数逼近程度，减小了经验选模的函数拟合误差.其次，通过运用双弹道的数据融合算法解算脱靶量参数，消除了传统算法在弹道参数衔接点的跳跃现象，并通过理论仿真和实测数据验证了算法的有效性.

矩阵构造，假设检验，回归模型，脱靶量

引言

空中目标脱靶量数据处理方法主要有基于同帧画幅的传统标准法、弹道高速摄影联合处理法、GPS弹道解算法、雷达径向测距的无线电法等.在脱靶量计算中，无论采用哪种方法都会用到三维坐标或距离的曲线拟合技术，并且不同的曲线拟合函数将会产生不同的脱靶量计算结果.由此可见，针对不同的弹道特性和测量数据，选用合适的处理模型，对提高脱靶量处理结果精度至关重要.

目前，上述几类方法均未给出拟合函数的选用准则，对模型的逼近阶也是基于经验确定.随着武器性能的提高，常规算法不一定能满足高精度的脱靶量数据处理需求.为有效解决脱靶量数据处理中的函数逼近选用问题，本文提出了基于假设检验的回归模型算法.通过设定初始高次函数，建立逼近函数的回归模型，运用假设检验理论，并充分结合测量数据进行模型定阶，从而确定合理的拟合函数.此方法依据严格的数学理论，避开了经验选模的风险.本文以光测相遇段数据处理方法为基础，通过改进算法进行仿真验证，结果表明此方法科学合理，脱靶量计算精度有所提高，目标参数衔接平稳，基本消除了弹道参数衔接点的跳跃现象.此方法扩展至其他脱靶量处理方法的模型选择，具有一定的实用参考价值.

1 脱靶量处理基本思路

常规光测脱靶量处理方法主要是对空中遭遇目标的光测观测信息进行处理.其算法的基本思路是选用某一目标的跟踪测量信息为基准，通过同帧画幅的处理技术去解算空中目标的脱靶量参数.

1.1 基准弹道计算

基准弹道是指空中目标相遇前后时间段的位置信息.对于目标基准弹道的计算，首先进行数据预处理，确保参与弹道计算的设备测元尽量“干净”.其次是进行弹道位置计算，可选用共面交会和异面交会方法，而不同算法各有其优缺点和算法适用性［1］.由于MLE法具有定位科学合理、适用范围大、交会精度高、设备布站灵活等特点，所以本文采用此方法.下面给出最大似然估计法弹道处理的数学表达式：

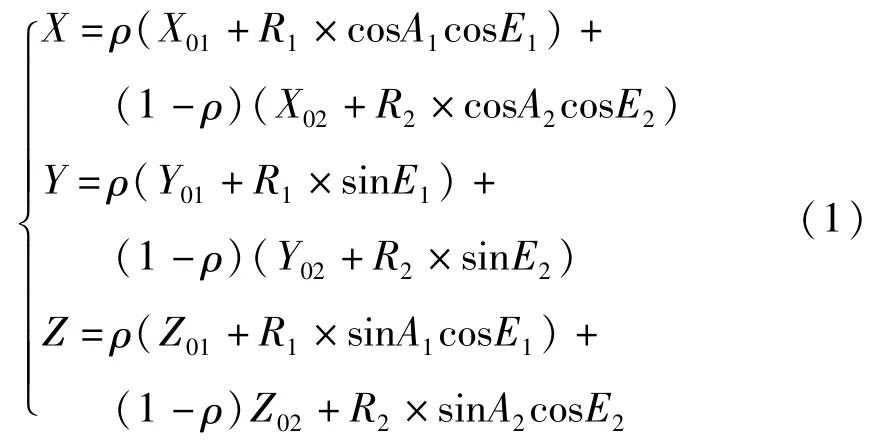
其中，

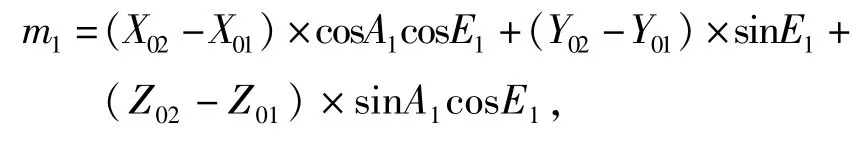
1.2 坐标反算角度

利用上面基准弹道计算结果，采用三维坐标的最小二乘拟合算法进行弹道拟合，按照给定条件计算目标相遇时段的坐标.坐标拟合系数计算公式为：

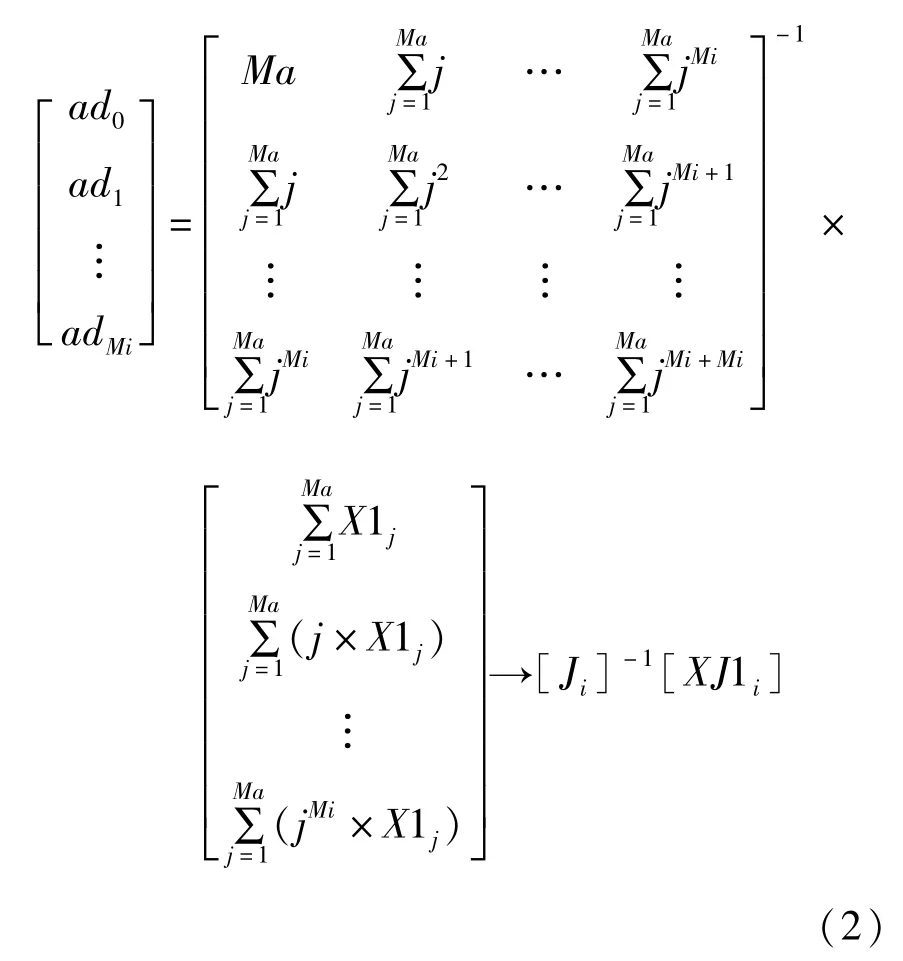
各时刻坐标计算为：

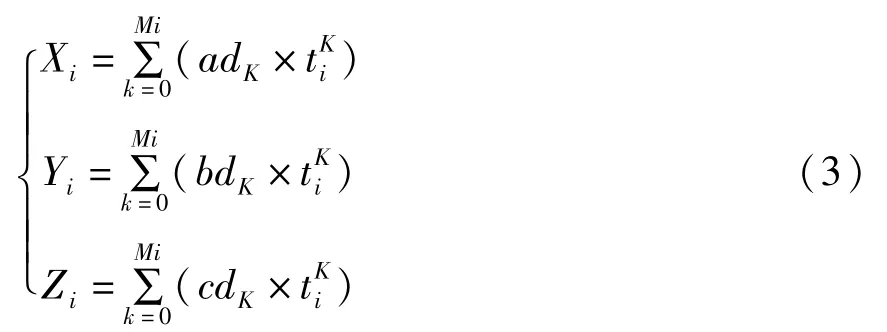
基准目标的同帧画幅角度反算为：

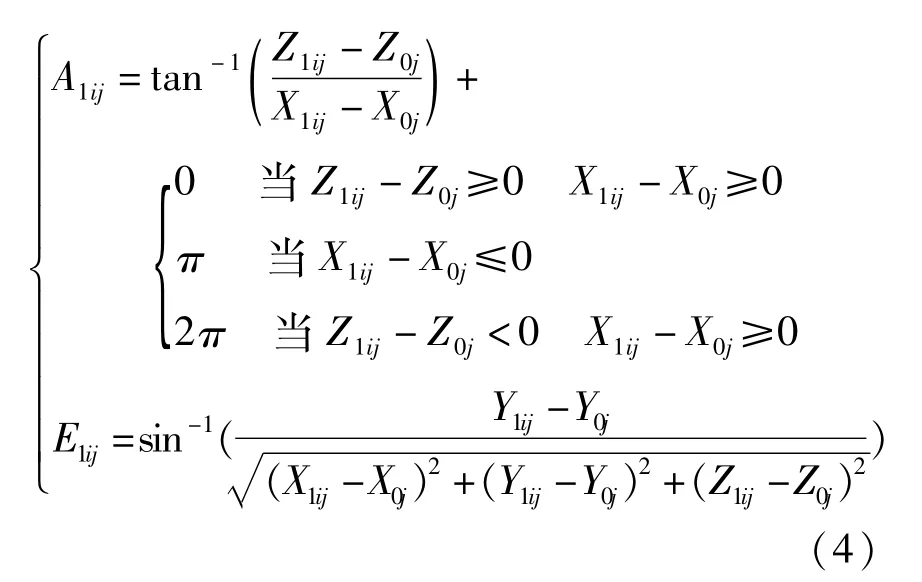
其中，X0j、Y0j、Z0j为各测站的站址坐标.

1.3 同帧画幅处理

同帧画幅是指目标相遇过程中，两个目标同时出现在同一台设备的观测画幅图像.其特点是两个目标的码盘角度一致，仅是跟踪脱靶量不同而已.同帧画幅处理技术正是利用这一特点，消除其相对误差，提高脱靶量数据处理精度.具体做法是将两目标的跟踪脱靶量差进行处理，求取另一目标的测量角度，从而进行目标弹道参数计算.

1.4 脱靶量参数计算

脱靶量参数主要求解脱靶时间、脱靶距离和炸点距离等.计算方法可参考传统标准法.

2 脱靶量计算方法改进

尽管常规的脱靶量数据处理方法计算的脱靶量参数精度较高，但从处理方法和模型上看，还有一些地方值得改进.下面以传统标准法为基础，从两个方面展开研究.一是函数模型的选取与定阶，二是多测元双弹道的联合处理.

2.1 基于假设检验的回归模型算法

基于假设检验的回归模型算法，主要是利用函数逼近理论，采用回归分析方法对逼近的函数进行合理选择和科学定阶，从而确定准确的弹道参数拟合函数，提高弹道轨迹拟合精度.

对弹道轨迹的拟合逼近，拟合函数和函数阶次的选择应遵循一定的客观实际和数学准则进行，本文采用的n次多项式进行弹道轨迹拟合.对拟合系数β进行回归系数检测，设计构造矩阵G和L，判断其若干个线性组合是否为零，检验Gβ＝0是否成立？若组合矩阵D非奇异，则在给定显著度水平α＝0，0.05或0.01的情况下再次判断，若FH＞FK，m－n（α）时否定Gβ＝0，否则接收Gβ＝0，从而确定拟合次数.针对武器试验的实际情况，可先设定4次函数作为初始条件，区分三种假设检验方案进行假设检验处理.

2.1.1 函数逼近模型初始设定

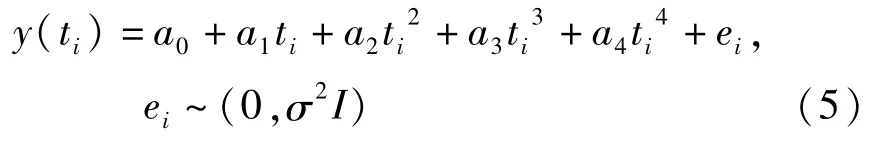
在进行拟合时，y（ti）和时间ti都是已知数，a0，a1，a2，a3，a4为回归模型待估系数，ei为随机误差.根据经验，数据采样点数与函数阶次拟合需求，一般情况下，采用点数是拟合阶次的10倍左右.

2.1.2 建立回归模型

Y＝Xm×nβn×1＋e 其中，m是测量数据组数，n是回归模型的待估系数的个数，e是随机误差.对于逼近区间的m组测量数据，写成矩阵形式的方程如下：

2.1.3 假设检验

假设对m组采样数据进行函数逼近，令：a0≠0，a1≠0，根据设定条件有三种假设方案：

（1）H1：a2＝a3＝a4＝0假设检验成立，回归模型则退化为一次函数；

（2）H2：a3＝a4＝0假设检验成立，回归模型则退化为二次函数；

（3）H3：a4＝0假设检验成立，回归模型则退化为三次函数.

假设检验过程：构造矩阵G，G为k×n矩阵，k≤n，rank（G）＝k，即G为满列秩矩阵.

当H1成立时，构造矩阵G1：

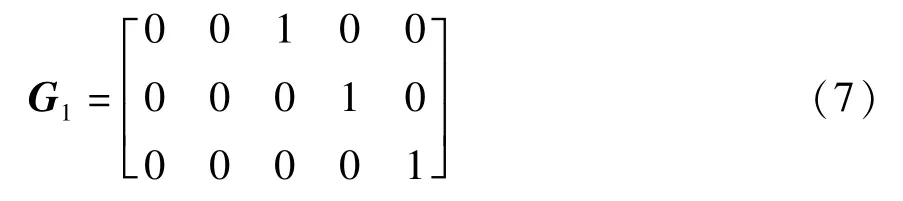
当H2成立时，构造矩阵G2：

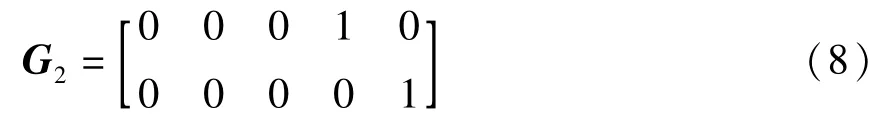
当H3成立时，构造矩阵G3：

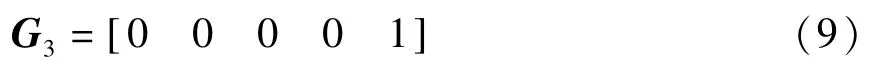
由矩阵论知识，存在（n－k）×n矩阵L，使得

为n阶非奇异阵，即对矩阵G进行扩维，构造成n阶方阵D.

对矩阵G1扩维成方阵D1的矩阵L1为：

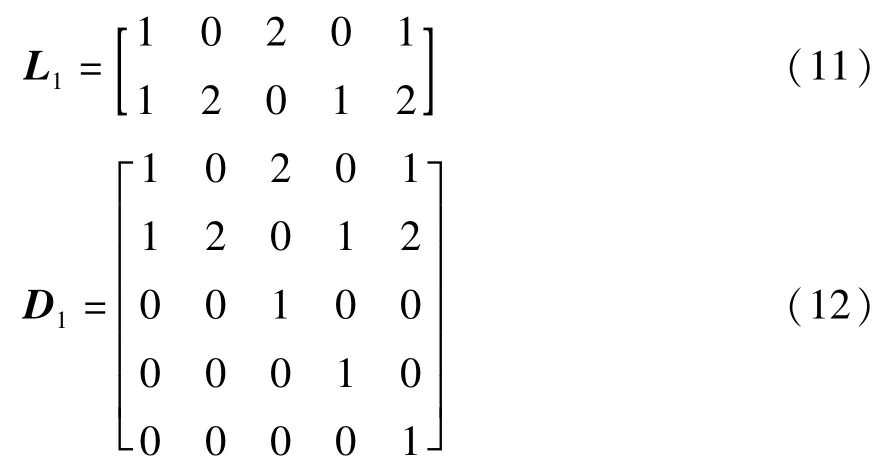
对矩阵G2扩维成方阵D2的矩阵L2为：

对矩阵G3扩维成方阵D3的矩阵L3为：

令Z＝XD－1，α＝Dβ，则有：

给定显著度水平α＝0.05或α＝0.01（通常情况取前者），可查表得 FK，m－n（α）的值，若FH＞FK，m－n（α），则否定本次假设，否则接收本次假设FH＜FK，m－n（α）.在否定假设的情况下，采取同样方式继续检验其他假设情况，直至找到接收的情况，确定准确的回归模型.

2.1.4 轨迹参数计算

采用确定的模型函数进行曲线拟合.输入计算的弹靶三维坐标和拟合时间，令S为残差平方和，再对此方程分别求βi的偏导数，令偏导数等于零，组成法方程组，带入坐标值和时间序列值，得到拟合曲线的拟合系数.输入时间序列值，带入到曲线拟合方程，求解导弹和靶标的轨迹参数.

2.2 双弹道联合处理脱靶量参数

传统标准法脱靶量数据处理，使用同帧画幅处理技术解算第二目标的位置参数与脱靶量，通常情况下选择不同目标作为基准弹道和不同的交会基线会处理出不同的脱靶量数值，并且第二目标的位置误差较大.尽管传统标准法能通过比较交会基线的条件筛选脱靶量数值，但不同交会方法也会产生一定的误差，影响脱靶量数据处理精度.

本文运用假设检验的回归模型算法，通过分别选取不同目标为基准弹道，结合传统标准法处理成弹靶四条弹道，然后采用双弹道多测元的数据融合方法计算目标位置和脱靶量参数.此算法不但确保了两目标的绝对定位精度和前后段落数据的平稳衔接，而且还保证了脱靶量参数的精度和处理结果的唯一性，在一定程度上弥补了传统标准法的不足.

3 算法验证

采用上述改进的假设检验回归模型脱靶量解算新方法，对不同几何尺寸目标、不同飞行速度、不同弹道特性、不同攻击条件以及不同制导方式的遭遇段数据进行仿真和实测数据测试，结果见表1.

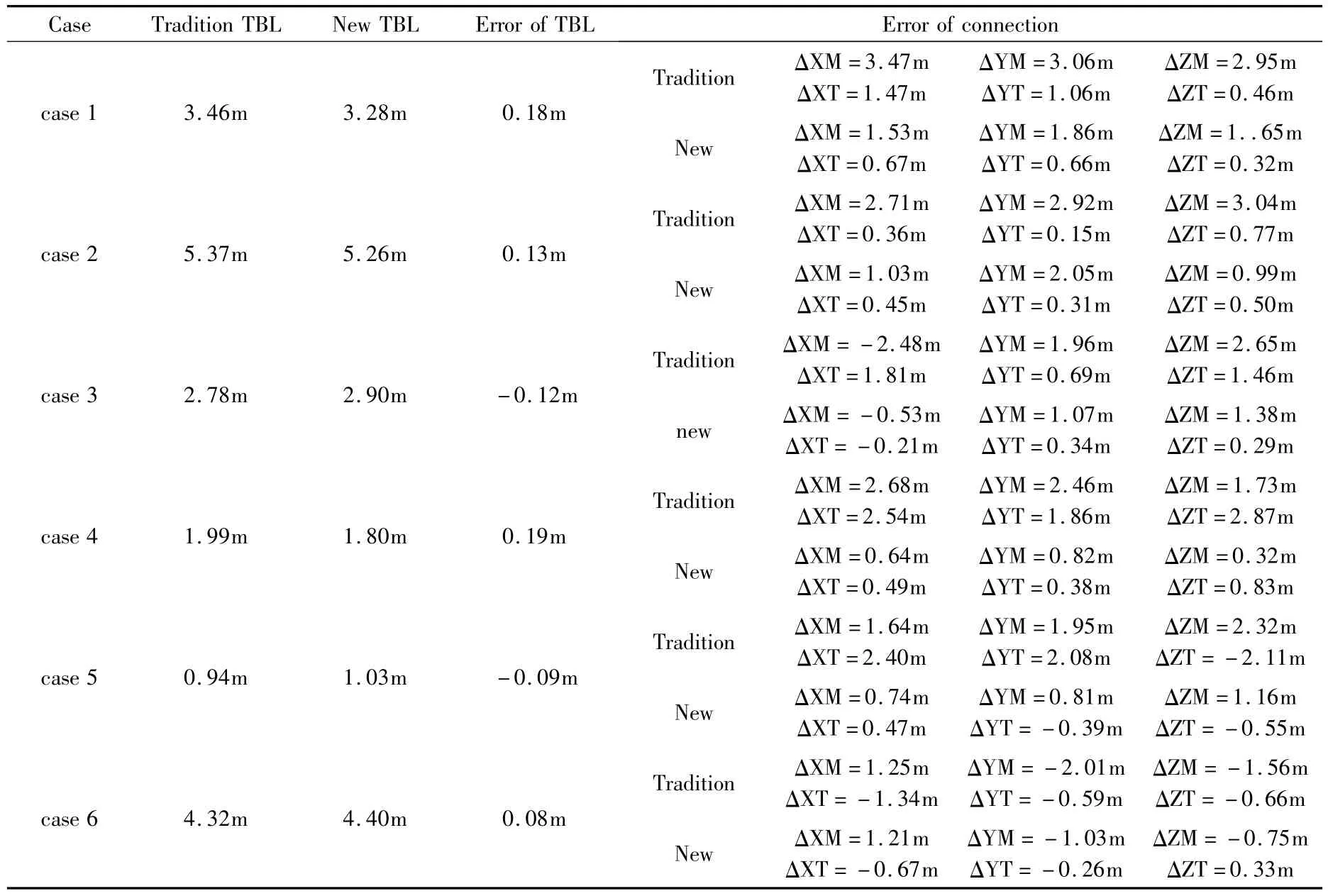
表1 两种方法比较Table 1 Comparison of two methods

结果表明，改进方法计算的脱靶量参数精度满足试验任务对数据处理的要求.该方法处理的遭遇段参数与弹道参数的衔接误差比传统标准法小，参数衔接更为平稳合理.

4 结论

本文通过改进相遇段脱靶量数据处理算法，给出了模型选择的数学理论依据，避免了经验选模的不足；同时，采用双弹道的数据融合技术，提高了弹道处理参数的定位精度和脱靶量数据处理精度，进而降低了弹道段与相遇段参数的衔接误差.从仿真和实测数据验证结果看，此方法合理，处理结果正确，在外测脱靶量数据处理中具有较强的推广使用价值.

1 王正明，易东云，周海银等.弹道跟踪数据的校准与评估.长沙：国防科技大学出版社，1999（Wang ZM，Yi D Y，Zhou H Y.Calibration and evaluation of trajectory tracking data.Changsha：National University of Defense Technology Press，1999（in Chinese））

2 王正明，易东云.测量数据建模与参数估计.长沙：国防科技大学出版社，1996（Wang ZM，Yi D Y.Model establishment and parameter estimation of measured data.Changsha：National University of Defense Technology Press，1996（in Chinese））

3 朱炬波，贺明科.自由节点样条函数平滑滤波技术.电子学报，2004，32（1）：27～30（Zhu JB，He M K.Data smoothing and filtering technique by free node spline function.Acta Eletronica Sinica，2004，32（1）：27～30（in Chinese））

4 刘利生.外测数据事后处理.北京：国防工业出版社，2000（Liu L S.Post-Flight data processing of trajectory measurement.Beijing：National Defense Industry Press，2000（in Chinese））

5 任晓庆，杜承烈.数据融合关键技术在靶场实验系统中的应用.计算机测量与控制，2005，13（10）：1098～1101（Ren X Q，Du C L.Applications of data fusion key technologies on shooting range testing system.Computer Measurement＆Control，2005，13（10）：1098～1101（in Chinese））

6 杨增学，杨世宏等.常规兵器试验交会测量方法及应用.西安：西安交通大学出版社，2010：78～85（Yang Z X，Yang S H et al.Measurement method and application of conventional weapon test intersection.Xi′an：Xi′an Jiaotong University Press，2010：78～85（in Chinese））

7 姚尚，张承虎等.基于小波分析和多模融合的外弹道估计算法.动力学与控制学报，2013，11（2）：182～186（Yao S，Zhang CH etal.Missile ballistic estimation based on wavelet analysis and multi-model fusion.Journal of Dynamics and Control，2013，11（2）：182～186（in Chinese））

8 李正东.双传感器目标脱靶量数据融合处理的方法.现代电子工程，2001，（2）：42～46（Li Z D.Fusion processing method of target miss distance data based on two types of sensors.Modern Electronic Engineering，2001，（2）：42～46（in Chinese））

9 李秋顺，高玉新等.脱靶量光学测量处理精度分析.中国宇航学会导弹航天器发射技术研讨会论文集，2001，12（Li Q S，Gao Y X et al.Precision analysis of optical measurement of miss distance.Proceedings of the China Aerospace Society missile launch technology Conference，2001，12（in Chinese））

10 马淑芬.矢量脱靶量测量系统数据处理方法研究.2009，06（Ma SF.Research on data processing algorithm for vector miss distance measurement system.2009，06（in Chinese） ）

Received 18 November 2015，revised 29 May 2016.

†Corresponding author E-mail：ys＿kjsyxljd＠163.com

APPLICATION OF REGRESSION MODELS IN TARGET-MISSING QUANTITY RESOLVING BASED ON HYPOTHESIS TESTING*

Yao Shang†Yang Bo Hu Changcheng Lei Lei Li Bin
（Unit565 of14 Branche，Jiuquan 735018，China）

Accurately selecting the fitting function of trajectory is the key step to calculate the target-missing parameters properly in target-missing Quantity processing.In this paper，we firstly utilize the regression model with hypothesis testing，choose the reasonable fitting model and confirm the order-number of the function.It is found that this method improves the function approximation and decreases the error of fitting function during choosing the model based on our experience.Secondly，we calculate the parameters of target-missing using dual-trajectory data fusion algorithm.This method eliminates the jump phenomenon of the connections between the trajectory parameters.The results of real-data processing indicate that the algorithm proposed in this paper performs better than the traditional methods，which validate the feasibility and superiority of this approach.

matrix construction，hypothesis testing，regression model，target-missing quantity

10.6052／1672-6553-2016-047

2015-11-18收到第1稿，2016-05-29收到修改稿.

†通讯作者E-mail：ys＿kjsyxljd＠163.com