Lagrange系统的广义斜梯度表示*

楼智美王元斌

（1.绍兴文理学院物理系，绍兴 312000）（2.绍兴文理学院数学系，绍兴 312000）

Lagrange系统的广义斜梯度表示*

楼智美1†王元斌2

（1.绍兴文理学院物理系，绍兴 312000）（2.绍兴文理学院数学系，绍兴 312000）

提出广义斜梯度系统并研究其性质，给出非定常Lagrange系统成为广义斜梯度系统的条件，利用广义斜梯度系统的性质来研究力学系统的稳定性.举例说明结果的应用.

Lagrange系统，广义斜梯度系统，稳定性

引言

通常梯度系统的矩阵和函数都不含时间t.如果矩阵和函数都含时间t，则称为广义梯度系统.如果斜梯度系统的矩阵和函数都含时间t，则称为广义斜梯度系统.文献［1］指出，梯度系统特别适合用Lyapunov函数来研究.文献［2］给出斜梯度系统，但它们都不含时间.有关力学系统与梯度系统的关联研究已有一些结果，如文献［3－12］.本文将通常斜梯度系统推广到包含时间的情形，并将非定常Lagrange系统的方程在一定条件下化成广义斜梯度系统的方程，进而借助广义斜梯度系统来研究力学系统的稳定性.

1 广义斜梯度系统

通常斜梯度系统的方程为［2］

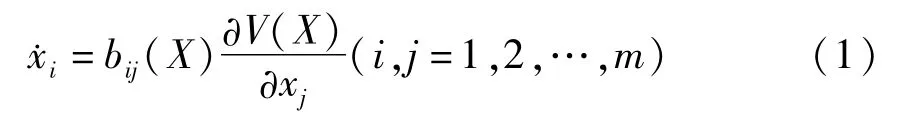
这里及以后相同指标表示求和，其中X＝（x1，x2，…，xm），bij（X）＝－bji（X）.将方程（1）推广到包含时间的情形，有

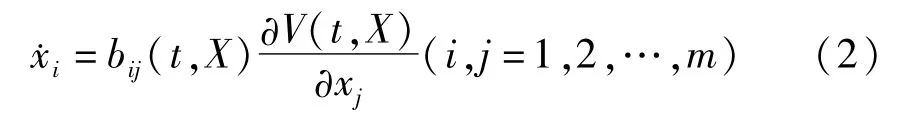
其中bij（t，X）＝－bji（t，X），称系统（2）为广义斜梯度系统.

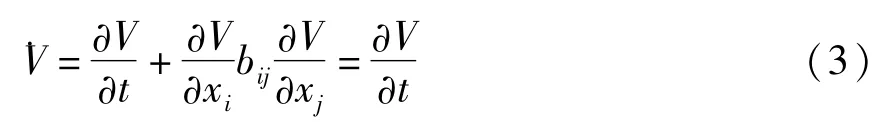
因此，对广义斜梯度系统（2），如果V＝V（t，0）＝0，V正定，且

则由Lyapunov定理知，解X＝0稳定.以上性质可用来研究可化成广义斜梯度系统的力学系统的稳定性.

2 Lagrange系统的梯度表示

Lagrange系统的微分方程为

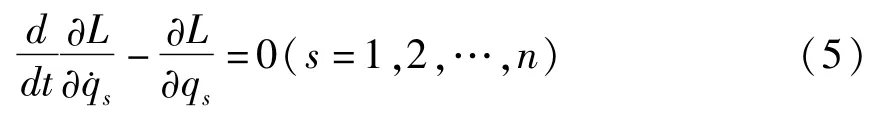
则由（5）式可解出所有广义加速度，记作

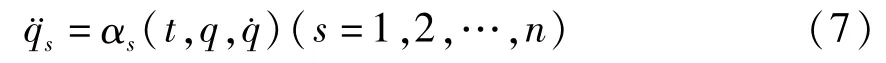
令

则方程（7）可写成如下形式

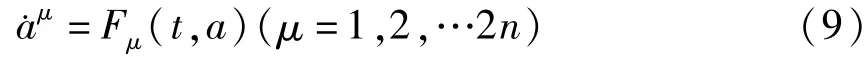
其中

引进广义动量ps和Hamilton函数H

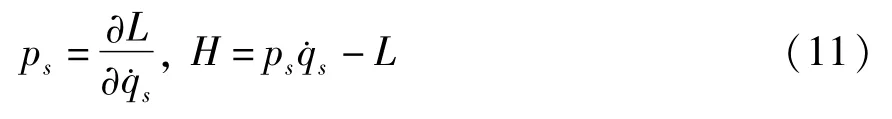
则方程（5）可写成

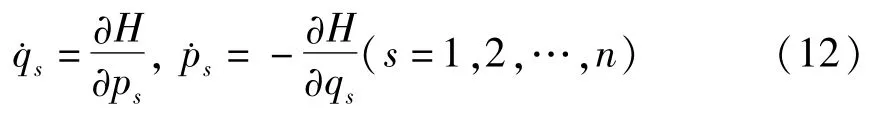
进而，方程（12）还可写成

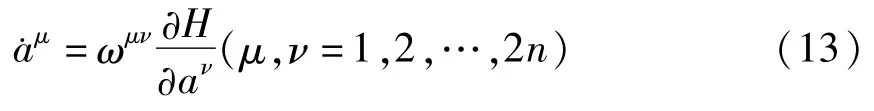
其中

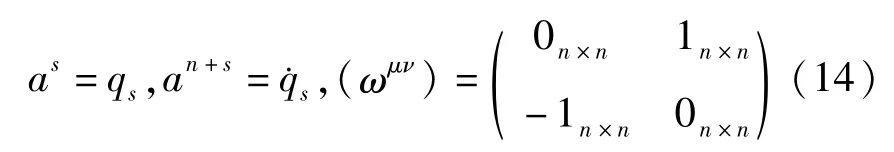
方程（9）或方程（13）一般不能成为广义斜梯度系统.对方程（9）如果存在反对称矩阵（bμν（t，a））和函数V＝V（t，a）满足下式

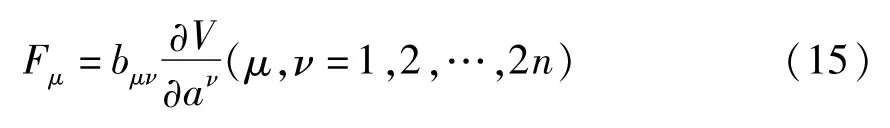
则它可以成为广义斜梯度系统.对方程（13），如果存在反对称矩阵（bμν（t，a））和函数V＝V（t，a）满足下式

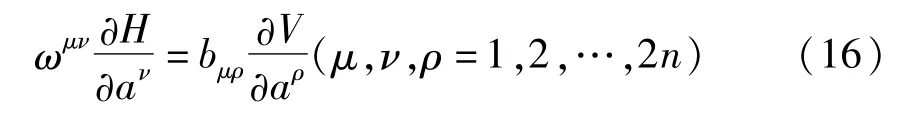
则它可以成为广义斜梯度系统.

值得注意的是，如果式（15）或式（16）不满足，还不能断定它不是广义斜梯度，因为这与方程（5）的一阶形式的选取相关.方程（5）的一阶形式可有多种选择，而式（9），式（13）是其中的两种.例如，还可选一部分a为q，另一部分a选为的线性式.对单自由度系统

可令

则有

取

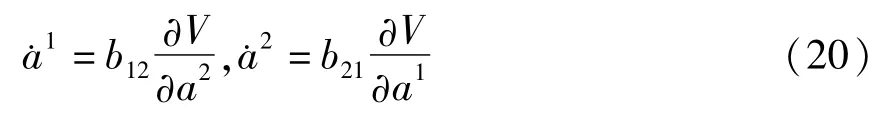
则有

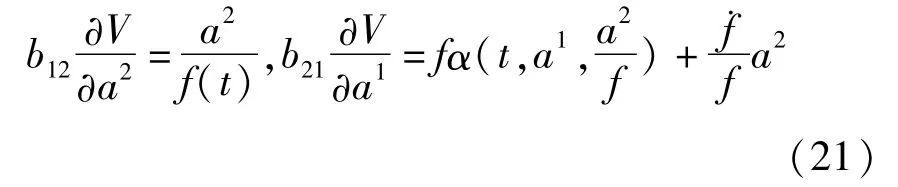
将第一个方程两边对a1求偏导数，将第二个方程两边对a2求偏导数，分别得到

这样，对给出的α，可按式（22）选b12，V，f使之成为广义斜梯度系统.如果

则有

3 算例

例1 单自由度系统为

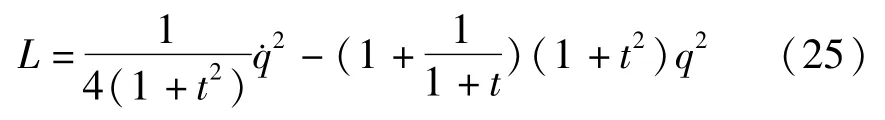
试将其化成广义斜梯度系统，并研究零解的稳定性.

解：将式（25）代入式（5）可得

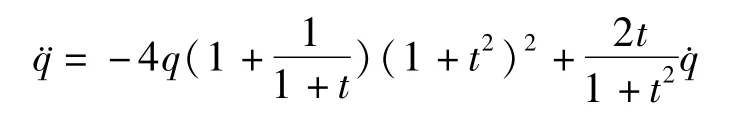
若按方程（9）或方程（13）选取a1，a2，还不能成为广义斜梯度系统.现令

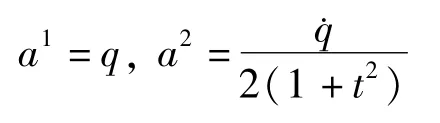
则有

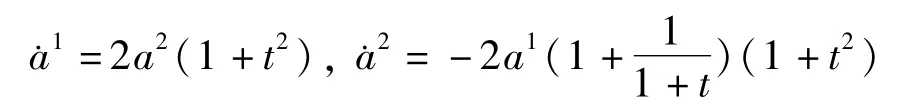
它可写成形式

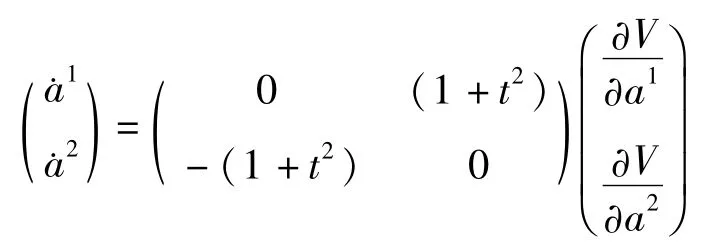
其中矩阵是反对称的，而函数V为

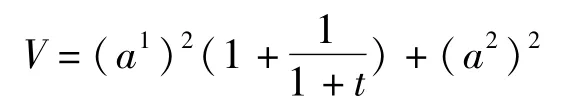
它在a1＝a2＝0邻域内是正定的，且有

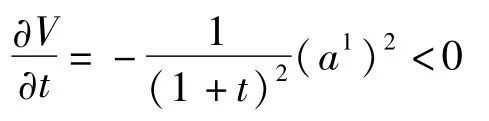
因此，零解a1＝a2＝0是稳定的.

对比式（24），所选

满足式（24）.

例2单自由度系统为

试将其化成广义斜梯度系统，并研究零解的稳定性.

解：将式（26）代入式（5）可得

为将其化成广义斜梯度系统，可按式（23），（24）计算.令

则有

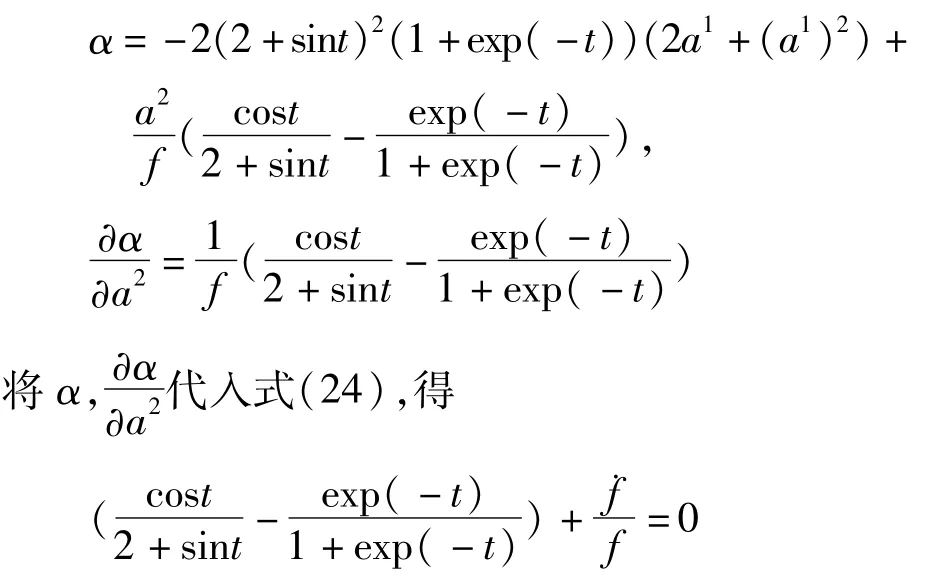
由此可得

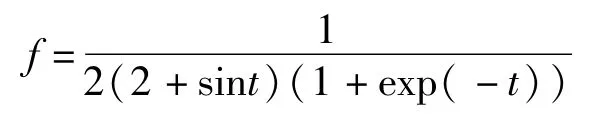
这样就有

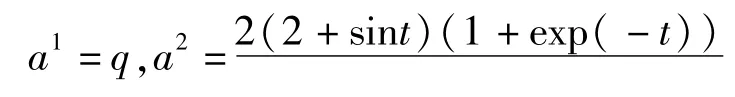
而方程（19）成为

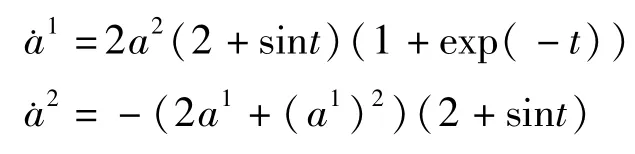
它可写成形式

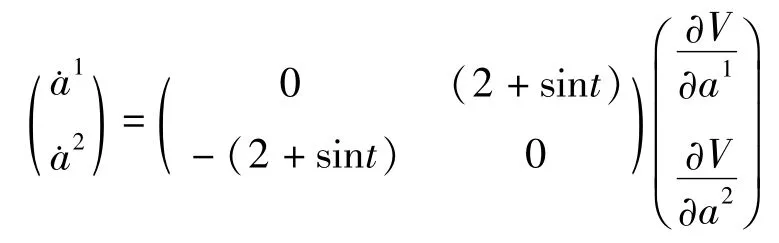
其中

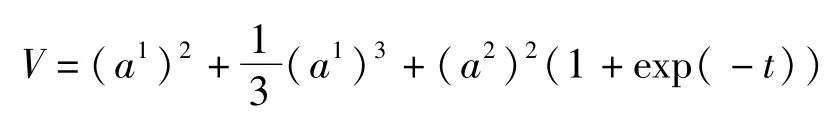
它在a1＝a2＝0邻域内正定，且

因此，零解a1＝a2＝0是稳定的.

4 结论

非定常力学系统的稳定性研究是一困难问题，直接从微分方程出发来构造Lyapunov函数往往不易实现.本文通过广义斜梯度系统来研究一些非定常Lagrange系统的稳定性问题.力学系统一旦成为广义斜梯度系统，并且使V＝V（t，a）成为Lyapunov函数，那么只要满足就可判断系统的稳定性.

1 Hirsch M W，Smale S，Devaney R L.Differential equations，dynamical systems and an introduction to chaos.Singapore：Elsevier，2008

2 Mclachlan R I，Quispel G RW，Robidoux N.Geometric integration using discrete gradients.Philosophical Transactions of the Royal Society A，1999，357：1021～1045

3 梅凤翔.关于梯度系统.力学与实践，2012，34（1）：89～90（Mei F X.On the gradient system.Mechanics in Engineering，2012，34（1）：89～90（in Chinese））

4 梅凤翔，吴惠彬.广义Birkhoff系统的梯度表示.动力学与控制学报，2012，10（4）：289～292（Mei F X，Wu H B.A gradient representation of generalized Birkhoff system.Journal of Dynamicsand Control，2012，10（4）：289～292（in Chinese））

5 楼智美，梅凤翔.力学系统的二阶梯度表示.物理学报，2012，61（2）：024502（Lou ZM，Mei F X.A second order gradient representation ofmechanics system.Acta Physica Sinica，2012，61（2）：024502（in Chinese））

6 梅凤翔，崔金超，吴惠彬.Birkhoff系统的梯度表示和分数维梯度表示.北京理工大学学报，2012，32（12）：1298～1300（Mei F X，Cui JC，Wu H B.A gradient representation and a fractional gradient representation of Birkhoff system.Journal of Beijing Institute of Technology，2012，32（12）：1298～1300（in Chinese））

7 梅凤翔.分析力学Ⅱ.北京：北京理工大学出版社，2013（Mei F X.2013 Analytical mechanics Ⅱ.Beijing：Beijing Institute of Technology Press（in Chinese））

8 葛伟宽，薛纭，楼智美.完整力学系统的广义梯度表示.物理学报，2014，63（11）：110202（Ge W K，Xue Y，Lou ZM.Generalized gradient representation of holonomic me-chanical systems.Acta Physica Sinica，2014，63（11）：110202（in Chinese））

9 梅凤翔，吴惠彬.事件空间中完整力学系统的梯度表示.物理学报，2015，64（23）：234501（Mei F X，Wu H B.A gradient representation of holonomic system in the event space.Acta Physica Sinica，2015，64（23）：234501（in Chinese））

10 Mei FX，Wu H B.Skew-gradient representation of generalized Birkhoffian system.Chinese Physics B，2015，24（10）：104502

11 梅凤翔，吴惠彬.一阶Lagrange系统的梯度表示.物理学报，2013，62（21）：214501（Mei F X，Wu H B.A gradient representation of first-order Lagrange system.Acta Physica Sinica，2013，62（21）：214501（in Chinese））

12 Mei F X，Cai J C.Skew-gradient representation of constrained mechanical systems.Applied Mathematics and Mechanics，2015，36（7）：873～882

*The project supported by the National Natural Science Foundation of China（11472177）

†Corresponding author E-mail：louzhimei＠usx.edu.cn

GENERALIZED SKEW-GRADIENT REPRESENTATION FOR LAGRANGE SYSTEM*

Lou Zhimei1†Wang Yuanbin2
（1.Department of Physics，Shaoxing University，Shaoxing 312000，China）
（2.Department of Mathematics，Shaoxing University，Shaoxing 312000，China）

A generalized skew-gradient system is proposed，and the characteristic of the system is also studied.Additionally，the condition under which a Lagrange system can be considered as a generalized skew-gradient system is obtained.It shows that the characteristic of the generalized skew-gradient system can be used to study the stability of the mechanics system.Moreover，some examples are given to illustrate the application of the results.

lagrange system，generalized skew-gradient system，stability Received 25 January 2016，revised 25 February 2016.

10.6052／1672-6553-2016-020

2016-01-25收到第1稿，2016-02-25收到修改稿.

*国家自然科学基金资助项目（11472177）

†通讯作者E-mail：louzhimei＠usx.edu.cn