基于L1范数的二维鉴别局部保留投影的最大间距准则方法

谢玉凯，卢桂馥，宣东东

(安徽工程大学计算机与信息学院，安徽 芜湖 241000)

基于L1范数的二维鉴别局部保留投影的最大间距准则方法

谢玉凯，卢桂馥，宣东东

(安徽工程大学计算机与信息学院，安徽 芜湖 241000)

为避免基于L1范数的鉴别局部保留投影(DLPP-L1)方法中图像数据向量化引起的矩阵计算的不稳定问题，提出了一种基于L1范数的二维鉴别局部保留投影的最大间距准则方法(2DDLPP-L1/MMC),目的是寻找一组最优投影向量使得投影变换后特征空间的类间离散度最大而类内离散度最小。2DDLPP-L1/MMC方法直接基于图像矩阵并且利用了L1范数对野值处理的稳健性以及最大间距准则所具有的优势，降低了计算量。人脸数据库上的试验结果表明，该方法具有较强的鲁棒性和较高的识别率。

鉴别局部保留投影；L1范数；最大间距准则；鲁棒性

在模式识别和机器学习领域中，数据中包含了很多的属性和特征，使得数据都是以高维形式存在的，导致维数灾难困扰着多种模式识别技术的应用和研究。为了解决高维数据面临的一系列问题并使后续的数据应用的更加稳健，就需要对高维数据进行降维。目前最常用的2种降维方法是主成分分析(PCA)[1,2]和线性判别分析(LDA)[3,4]。PCA通过找寻一组最佳的正交投影向量，使投影后的数据方差最大化从而尽可能多的存储可分性信息。然而，传统的PCA忽略了类别属性，重要的可分性信息也许包含在被忽略的投影方向中。LDA作为一种有监督的学习方法利用了该类别属性，该方法的最佳投影方向是通过求解Fisher准则函数最大化而获得，使得原始样本向这组向量投影后的特征空间的类内离散度最小，类间离散度最大。然而，LDA总是遭遇小样本问题，这主要是特征空间的维数高于训练样本的总数，继而导致类内协方差矩阵的奇异性和不稳定性问题。

最近，He和Niyogi提出了一种新的特征提取方法，即局部保留投影(LPP)[5]。LPP是Laplacian Eigemap的一个线性投影方法，其本质是通过一个线性投影，尽可能的保持原始样本数据在高维空间里的局部几何结构以获得良好的低维可视化效果。但是LPP不能利用训练数据中的判别属性。为此，文献[6]提出了一种鉴别局部保留投影方法(Discriminant Locality Preserving Projection,DLPP),它通过在LPP中增加判别信息来充分利用类别信息。

从统计的角度来看，相比于L2范数，L1范数对野值更具鲁棒性，因为L1范数中的绝对值操作减轻了对野值的影响。基于此，基于L1范数的相关方法开始被提出来，如基于L1范数的PCA[7,8]，基于L1范数的LDA[9,10]。PCA-L1实际上是将PCA模型中的L2范数改为L1范数来进行求解，其局部最优投影向量通过对特征空间中的基于L1范数的方差实现最大化求解而得到，但是PCA-L1计算较为复杂并且样本数据中的类别属性没有得到运用。LDA-L1是将LDA模型中的L2范数改为L1范数来进行求解，在特征空间中使基于L1范数的类间散度和基于L1范数的类内散度的比率达到最大化的投影向量作为局部最优的投影向量。但是DLPP-L2[6]是基于L2范数的，L2范数中平方操作会放大野值的影响。

受L1范数启发，一种基于L1范数的鉴别局部保留投影(DLPP-L1)[11]被提了出来，其目标函数是基于L1范数的。此外，文献[12,13]提出了一种运用最大间距准则(MMC)思想的特征提取方法。在几何角度上，基于MMC的特征提取是通过最大化类间散度与类内散度之间的差值求解出一组最优的投影向量集进行投影，从而实现最大化类间散度，最小化类内散度的目标。此外，注意到MMC方法和MMC-L1这些方法在处理训练样本过程中都是基于一维向量来求解。为此，考虑直接对图像数据矩阵进行降维的可行性，笔者对DLPP-L1方法进行改进，提出了一种基于L1范数的二维鉴别局部保留投影的最大间距准则方法(2DDLPP-L1/MMC)。

1 问题的提出

在分离图中第i个顶点和第j个顶点之间的边被定义为第i类和第j类之间均值矩阵的权重：

式中,σb是一个调节因子。

式中,σw是一个调节因子。

对图像数据进行降维操作时，需要最大化特征空间中分离图的类间离散度Jb(w)：

(1)

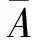
与此同时，最小化特征空间中内聚图的类内离散度Jw(w)：

(2)

因此，MMC最终的目标函数旨在解决最优化问题(3)，以寻求最佳鉴别矢量为投影轴进行投影变换：

(3)

其中，A=[a(1),a(2),…,a(m)]T，a(l)(l=1,…,m)指的是A的第l行的列向量形式，即A的第l行为a(l)的转置；|·| 表示绝对值操作； ‖·‖1表示L1范数；α是权重参数，用来调节不同类别情况下分离图的类间离散度和内聚图的类内离散度对特征提取的影响；L1范数指向量中各个元素绝对值之和；L2范数指向量中各元素平方和然后求平方根。如果采用L2范数优化求解上述问题，其中的平方操作会放大噪声的负面影响。

2 2DDLPP-L1/MMC提取单个投影向量

最优投影方向w可以通过梯度法迭代求解出。由于数学上绝对值操作不可微分，而目标函数J(w(t))中又留有绝对值符号，所以，在这里笔者定义2个符号函数来解除绝对值对目标函数的影响，在第t步迭代过程中，定义的符号函数如下：

(4)

(5)

i,j=1,…,Nkk=1,…,cl=1,…,m

把式(4)和式(5)代入式(3)得到：

(6)

通过w(t+1)=w(t)+γg(t)来更新最优投影方向w(t)，其中：

(7)

式中，γ表示学习步长，是一个非常小的正值(0<γ<1)。

最优投影向量w通过式(4)、式(5)和式(7)的循环交替求解出，如果J(w(t+1))在后续的迭代过程中不再保持增长，那么终止循环操作。否则，对式(4)和式(5)符号函数进行更新操作，然后继续循环操作，一直到有符合条件的投影向量w出现。

式(4)、式(5)符号函数与式(7)梯度公式在每次循环交替计算当中，表明式(6)中的目标函数J(w(t+1))>J(w(t))，即J(w(t))一直维持着非降。那么对式(4)、式(5)符号函数与式(7)梯度公式的循环交替处理会使得迭代求解渐渐达到一个收敛的过程，但是，目标函数通过优化迭代方法求解出的投影向量w是基于局部最优的，并不符合全局最优解的条件。因此笔者尝试挑选出一系列w(0)初始化值来运行这个迭代优化算法以最大限度的找寻到最佳的目标函数最大值。

2DDLPP-L1/MMC单个投影向量的算法(算法1)步骤如下：

输出：单个投影向量w*。

1)初始化：设迭代次数t=0，生成一个s维的非零向量w(0)，并且归一化w(0)=w(0)/‖w(0)‖2。

3)计算符号函数：

4)更新为w(t+1)=w(t)+γg(t)，其中γ>0是一个调节因子:

5)判断是否收敛：若J(w(t+1))停止增长，则终止循环，并令w*=w(t+1)。否则，令t=t+1，返回步3)并继续向下执行，直到找到符合条件的投影向量。

3 2DDLPP-L1/MMC求取多个投影向量

上面所述的迭代方法只能提取出一个最优投影向量，实际应用中，这是远远不够的，所以有必要扩展到提取多个投影向量。为了求取r个投影向量，笔者采用一种紧缩的方法来提取剩余的基向量。

设Xl=(xl1,…,xln)∈Rd×n，1≤l≤d。第r个基向量wr可通过求解如下问题来提取：

(8)

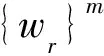
输出：w1，w2，…，wm，因此W=(w1，w2，…，wm)。

2)h=1,…,m，执行以下迭代操作。计算：

对数据集Th调用算法1，提取wh。

4 试验

为了验证所提出的2DDLPP-L1/MMC方法较其他相关方法的性能优势，笔者在0RL人脸数据库上进行试验验证。ORL人脸数据库中包含40人总共400张人脸图像，每人10张不同表情和姿态条件下的面部图像。试验中，图像处理成灰度级为256，分辨率为112×92的形式。编程环境为Matlab 2014，操作系统为Windows 7。同类试验在设置参数上不能出现差异，要保持一致，以确保试验的公平与结果的可靠。

4.1 权重参数α对识别率的影响

权重参数α平衡最大化分离图的类间离散度和最小化内聚图的类内离散度2个不同目标，为了评估权重参数对2DDLPP-L1/MMC方法的识别率的影响，试验选用的训练样本为ORL数据库中每类前一半图像，余下的作为测试样本,把权重参数α依序设置为0.0001、0.0005、0.001、0.005、0.01、0.05、0.1、0.5、1、5、10，试验结果如图1所示。

由图1可知，当权重参数α逐步增加时，2DDLPP-L1/MMC方法的识别率逐渐稳步上升，随后开始趋于平缓，当权重参数足够大时，该方法的识别率又开始逐渐平缓的下降。由此可知，权重参数α对2DDLPP-L1/MMC识别率有着潜移默化的影响，而选用一个合适的α值相当重要。因此，在后面的试验中均选择了较为合理的α值，以最大化发挥2DDLPP-L1/MMC方法的性能。

4.2 训练集大小对识别率的影响

训练集大小对识别率有着较大的影响，试验中选择ORL人脸数据库中每类前n(n=3,4,5,6,7,8)幅图像作为训练样本，余下的图像作为测试样本，以此来测试各种方法的识别性能。为了保持试验结果的公平与合理性，所有方法的投影轴数都设置成20个，结果如图2所示。

由图2可知，在其他条件相同的情况下，各种方法的识别率在训练样本数开始逐步增加时都呈现出稳步上升的趋势，随后趋于缓慢提高。这表明训练样本数的大小影响着各种方法的识别率，与此同时，2DDLPP-L1/MMC方法的识别率相比较于其他方法一直是较高的。

4.3 投影轴数对识别率的影响

投影轴数对识别率的有着较大的影响，试验选用ORL人脸数据库中每类前5幅图像当做训练样本，余下图像作为测试样本，依次选择1、2、…,20个投影轴数来检验各种方法的识别性能，结果如图3所示。

图1 权重参数α对识别率的影响 图2 训练集大小对识别率的影响

图3 投影轴数对识别率的影响

由图3可知，各种方法的识别率随着投影轴数不断增加都开始逐步上升，随后各种方法识别率上升的趋势趋于饱和平缓，当投影轴数大于20时识别率都会有进一步缓缓上升的趋势。图3显示，2DDLPP-L1/MMC方法的识别率明显要高于其他方法，因此，其判别性能要好于其他方法。

5 结语

提出了基于L1范数的二维鉴别局部保留投影的最大间距准则方法(2DDLPP-L1/MMC)。2DDLPP-L1/MMC直接基于图像矩阵空间充分利用L1范数及最大间距准则的相关优势来提取低维特征，从而避免了矩阵计算的复杂性和不稳定性。并且，笔者提出了一个优化迭代算法来求解最优投影矩阵，同时增强了对异常值的鲁棒性。试验结果证明，该方法的识别性能和其他相关方法相比更加高效。值得注意的是，该算法由于只是收敛到局部最优并不能达到全局最优的条件，所以有待进一步完善，未来要开展的工作中主要是研究如何找到全局最优。

[1]Turk M, Pentland A.Eigenfaces for Recognition.J Cogn Neurosci[J].Journal of Cognitive Neuroscience, 1991, 3(1):71～86.

[2] Akbari R, Mozaffari S.Performance enhancement of PCA-based face recognition system via gender classification method[J].2010, 1(1):1～6.

[3] Yu H, Yang J.A direct LDA algorithm for high-dimensional data -with application to face recognition[J].Pattern Recognition, 2001, 34(10):2067～2070.

[4] Huang J, Yuen P C, Chen W S, et al.Choosing Parameters of Kernel Subspace LDA for Recognition of Face Images Under Pose and Illumination Variations[J].IEEE Transactions on Systems Man & Cybernetics Part B Cybernetics A Publication of the IEEE Systems Man & Cybernetics Society, 2007, 37(4):847～862.

[5] He X, Niyogi P.Locality Preserving Projections (LPP)[J].Advances in Neural Information Processing Systems, 2002, 16(1):186～197.

[6] Yu W, Teng X, Liu C, et al.Face recognition using discriminant locality preserving projections[J].Image and Vision Computing, 2006, 24(3): 239～248.

[7] Kwak N.Principal component analysis based on l1-norm maximization[J].IEEE Transactions on Pattern Analysis & Machine Intelligence, 2008, 30(9):1672～1680.

[8] Nie F, Huang H, Ding C, et al.Robust Principal Component Analysis with Non-Greedy 1-Norm Maximization[C].International Joint Conference on Artificial Intelligence,2011:1433～1438.

[9] Zhong F, Zhang J.Linear discriminant analysis based on L1-norm maximization[J].IEEE Transactions on Image Processing, 2013, 22(8):3018～3027.

[10] Liu Y, Gao Q, Miao S, et al.A Non-greedy Algorithm for L1-norm LDA[J].IEEE Transactions on Image Processing A Publication of the IEEE Signal Processing Society, 2016, PP(99):1～1.

[11] Zhong F, Zhang J, Li D, et al.Discriminant Locality Preserving Projections Based on L1-Norm Maximization[J].IEEE Transactions on Neural Networks, 2014, 25(11): 2065～2074.

[12] Li H, Jiang T, Zhang K.Efficient and robust feature extraction by maximum margin criterion[J].IEEE Transactions on Neural Networks, 2006, 17(1):157～165.

[13] Song F, Zhang D, Chen Q, et al.Face recognition based on a novel linear discriminant criterion[J].Pattern Analysis and Applications, 2007, 10(3):165～174.

[编辑] 洪云飞

2017-01-27

国家自然科学基金项目(61572033,71371012)；安徽高校自然科学研究项目(重大项目)(KJ2015ZD08)；教育部人文社会科学规划项目(13YJA630098)。

谢玉凯(1990-)，男，硕士生，现主要从事计算机视觉方面的研究工作，1509739519@qq.com。

TP391.4

A

1673-1409(2017)09-0038-05

[引著格式]谢玉凯，卢桂馥，宣东东.基于L1范数的二维鉴别局部保留投影的最大间距准则方法[J].长江大学学报(自科版)，2017,14(9)：38～42，78.